注釈
このページは docs/tutorials/10_warm_start_qaoa.ipynb から生成されました。
ウォーム・スタート・量子最適化#
はじめに#
整数変数や制約による最適化問題は、しばしば解くのが困難です。例えば、制約なし二次形式二値変数最適化(QUBO)問題 、すなわち
\begin{align} \min_{x\in\{0,1\}^n}x^T\Sigma x + \mu^Tx, \end{align}
は NP-Hard です。ここで、\(\Sigma\) は \(n\times n\) 行列で \(x\) は \(n\) 次のバイナリー値のベクトルです。ここで \(x_i^2=x_i\) for \(x_i\in\{0, 1\}\) なので対角成分に線形項 \(\mu\) を加えても良いことに注意してください。QUBO は解くのが難しいですが、解きやすい問題に緩和するたくさんの方法があります。例えば、もし \(\Sigma\) が半正定値ならば QUBO は凸二次最適化問題に帰着します。
\begin{align} \min_{x\in[0,1]^n}x^T\Sigma x, \end{align}
これは \(x\) で簡単に解けるようになりました。ここで \(n\) は \([0, 1]\) の範囲の連続変数です。このような緩和は [1] にあるように、ウォーム・スタート量子最適化問題に活用できます。
参考文献#
[1] D. J. Egger, J Marecek, S. Woerner, Warm-starting quantum optimization, arXiv:2009.10095
[1]:
import numpy as np
import copy
# Problem modelling imports
from docplex.mp.model import Model
# Qiskit imports
from qiskit_algorithms import QAOA, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import COBYLA
from qiskit_algorithms.utils.algorithm_globals import algorithm_globals
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import MinimumEigenOptimizer, CplexOptimizer
from qiskit_optimization import QuadraticProgram
from qiskit_optimization.problems.variable import VarType
from qiskit_optimization.converters.quadratic_program_to_qubo import QuadraticProgramToQubo
from qiskit_optimization.translators import from_docplex_mp
準備:QUBO の緩和#
まず、半確定正の行列で構築された QUBO をリラックスして、解決しやすい QP を実現する方法を説明します。
[2]:
def create_problem(mu: np.array, sigma: np.array, total: int = 3) -> QuadraticProgram:
"""Solve the quadratic program using docplex."""
mdl = Model()
x = [mdl.binary_var("x%s" % i) for i in range(len(sigma))]
objective = mdl.sum([mu[i] * x[i] for i in range(len(mu))])
objective -= 2 * mdl.sum(
[sigma[i, j] * x[i] * x[j] for i in range(len(mu)) for j in range(len(mu))]
)
mdl.maximize(objective)
cost = mdl.sum(x)
mdl.add_constraint(cost == total)
qp = from_docplex_mp(mdl)
return qp
def relax_problem(problem) -> QuadraticProgram:
"""Change all variables to continuous."""
relaxed_problem = copy.deepcopy(problem)
for variable in relaxed_problem.variables:
variable.vartype = VarType.CONTINUOUS
return relaxed_problem
この例では、以下に定義する半正定値行列 \(\Sigma\) と線形項 \(\mu\) を使用します。
[3]:
mu = np.array([3.418, 2.0913, 6.2415, 4.4436, 10.892, 3.4051])
sigma = np.array(
[
[1.07978412, 0.00768914, 0.11227606, -0.06842969, -0.01016793, -0.00839765],
[0.00768914, 0.10922887, -0.03043424, -0.0020045, 0.00670929, 0.0147937],
[0.11227606, -0.03043424, 0.985353, 0.02307313, -0.05249785, 0.00904119],
[-0.06842969, -0.0020045, 0.02307313, 0.6043817, 0.03740115, -0.00945322],
[-0.01016793, 0.00670929, -0.05249785, 0.03740115, 0.79839634, 0.07616951],
[-0.00839765, 0.0147937, 0.00904119, -0.00945322, 0.07616951, 1.08464544],
]
)
DOCPLEXを使用して、バイナリ変数のモデルを構築します。
[4]:
qubo = create_problem(mu, sigma)
print(qubo.prettyprint())
Problem name: docplex_model1
Maximize
-2.15956824*x0^2 - 0.03075656*x0*x1 - 0.44910424*x0*x2 + 0.27371876*x0*x3
+ 0.04067172*x0*x4 + 0.0335906*x0*x5 - 0.21845774*x1^2 + 0.12173696*x1*x2
+ 0.008018*x1*x3 - 0.02683716*x1*x4 - 0.0591748*x1*x5 - 1.970706*x2^2
- 0.09229252*x2*x3 + 0.2099914*x2*x4 - 0.03616476*x2*x5 - 1.2087634*x3^2
- 0.1496046*x3*x4 + 0.03781288*x3*x5 - 1.59679268*x4^2 - 0.30467804*x4*x5
- 2.16929088*x5^2 + 3.418*x0 + 2.0913*x1 + 6.2415*x2 + 4.4436*x3 + 10.892*x4
+ 3.4051*x5
Subject to
Linear constraints (1)
x0 + x1 + x2 + x3 + x4 + x5 == 3 'c0'
Binary variables (6)
x0 x1 x2 x3 x4 x5
このようなバイナリー問題は扱いにくいですが、問題のインスタンスが十分に小さい場合は解くことができます。上記の例では次の解を持ちます。
[5]:
result = CplexOptimizer().solve(qubo)
print(result.prettyprint())
objective function value: 16.7689322
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS
この問題は変数がもはやバイナリーではない問題に緩和することができます。制約を2次ペナルティ項に変換するために、QuadraticProgramToQubo コンバーターを使用することに注意してください。Qiskit 最適化モジュールが内部的に適用するステップと整合性を保つためにこれを行います。
[6]:
qp = relax_problem(QuadraticProgramToQubo().convert(qubo))
print(qp.prettyprint())
Problem name: docplex_model1
Minimize
44.84880018*x0^2 + 85.40922044*x0*x1 + 85.82756812*x0*x2
+ 85.10474511999999*x0*x3 + 85.33779215999999*x0*x4 + 85.34487328*x0*x5
+ 42.90768968*x1^2 + 85.25672692*x1*x2 + 85.37044588*x1*x3 + 85.40530104*x1*x4
+ 85.43763867999999*x1*x5 + 44.65993794*x2^2 + 85.4707564*x2*x3
+ 85.16847247999999*x2*x4 + 85.41462863999999*x2*x5 + 43.89799534*x3^2
+ 85.52806848*x3*x4 + 85.34065100000001*x3*x5 + 44.28602462*x4^2
+ 85.68314192*x4*x5 + 44.85852282*x5^2 - 259.55339164*x0
- 258.22669163999996*x1 - 262.37689163999994*x2 - 260.57899163999997*x3
- 267.02739163999996*x4 - 259.54049163999997*x5 + 384.20308746
Subject to
No constraints
Continuous variables (6)
0 <= x0 <= 1
0 <= x1 <= 1
0 <= x2 <= 1
0 <= x3 <= 1
0 <= x4 <= 1
0 <= x5 <= 1
この連続的な緩和の解はバイナリー問題の解と異なりますが、バイナリー問題を扱う限りソルバーをウォーム・スタートするために使用することができます。
[7]:
sol = CplexOptimizer().solve(qp)
print(sol.prettyprint())
objective function value: -17.01205502568274
variable values: x0=0.17524995761801201, x1=1.4803888163984595e-07, x2=0.9709053264087679, x3=0.7384168677494151, x4=0.9999999916475085, x5=0.14438904470168346
status: SUCCESS
[8]:
c_stars = sol.samples[0].x
print(c_stars)
[0.17524995761801201, 1.4803888163984595e-07, 0.9709053264087679, 0.7384168677494151, 0.9999999916475085, 0.14438904470168346]
QAOA#
ここでは、上記の緩和された問題を活用することにより、量子近似最適化アルゴリズム ( QAOA) をウォーム・スタートする方法を説明します。
標準的な QAOA#
まず標準の QAOA を使用して、QUBOを解きます。これを行うために、QUBO を QuadraticProgram クラスに変換します (結果として生じる問題は依然としてバイナリー問題であることに注意してください) 。
[9]:
algorithm_globals.random_seed = 12345
qaoa_mes = QAOA(sampler=Sampler(), optimizer=COBYLA(), initial_point=[0.0, 1.0])
exact_mes = NumPyMinimumEigensolver()
[10]:
qaoa = MinimumEigenOptimizer(qaoa_mes)
[11]:
qaoa_result = qaoa.solve(qubo)
print(qaoa_result.prettyprint())
objective function value: 16.768932200000002
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS
ウォーム・スタート QAOA#
次に、この結果をウォーム・スタート QAOA と比較します。この QAOA には連続的な緩和を行った問題の解を使います。最初に、初期状態を作成します。
\begin{align} |\phi^*\rangle=\bigotimes_{i=0}^{n-1}R_y(\theta_i)|0\rangle_n . \end{align}
これは \(R_y\) 回転を角 \(\theta=2\arcsin(\sqrt{c^*_i})\) で適用することで与えられます。この角は緩和した問題の解に依存します。ここで \(c^*_i\) は緩和した問題の変数 \(i\) の値です。
[26]:
from qiskit import QuantumCircuit
thetas = [2 * np.arcsin(np.sqrt(c_star)) for c_star in c_stars]
init_qc = QuantumCircuit(len(sigma))
for idx, theta in enumerate(thetas):
init_qc.ry(theta, idx)
init_qc.draw(output="mpl", style="clifford")
[26]:
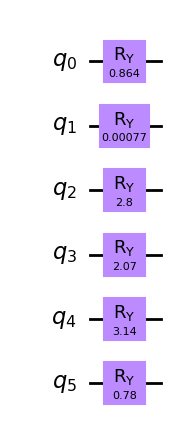
次に QAOA のミキサー演算子を作成します。ウォーム・スタート QAOA では、ミキサー演算子の初期状態が基底状態になっていることを確認する必要があります。そのため次のハミルトニアンを選びます
\begin{align} H_{M,i}^{(ws)}= \begin{pmatrix} 2c_i^*-1 & -2\sqrt{c_i^*(1-c_i^*)} \\ -2\sqrt{c_i^*(1-c_i^*)} & 1-2c_i^* \end{pmatrix} \end{align}
これは量子ビット \(i\) のミキサー演算子のハミルトニアンです。 \(-i\beta\) を乗じ指数をとると、このミキサーは次のミキサー回路を生成します。
[27]:
from qiskit.circuit import Parameter
beta = Parameter("β")
ws_mixer = QuantumCircuit(len(sigma))
for idx, theta in enumerate(thetas):
ws_mixer.ry(-theta, idx)
ws_mixer.rz(-2 * beta, idx)
ws_mixer.ry(theta, idx)
ws_mixer.draw(output="mpl", style="clifford")
[27]:
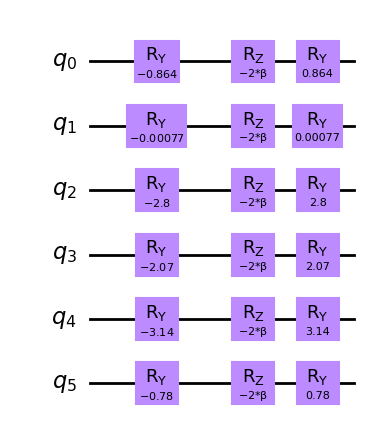
こうして初期状態とミキサー演算子は QAOA に渡すことができます。
[14]:
ws_qaoa_mes = QAOA(
sampler=Sampler(),
optimizer=COBYLA(),
initial_state=init_qc,
mixer=ws_mixer,
initial_point=[0.0, 1.0],
)
[15]:
ws_qaoa = MinimumEigenOptimizer(ws_qaoa_mes)
[16]:
ws_qaoa_result = ws_qaoa.solve(qubo)
print(ws_qaoa_result.prettyprint())
objective function value: 16.768932200000002
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS
分析#
どちらの結果も同じ結果を与えます。しかし、基礎となる確率分布を観察すると、ウォーム・スタート QAOA は最適なソリューションをサンプリングする確率が高くなることが観察されます。
[17]:
def format_qaoa_samples(samples, max_len: int = 10):
qaoa_res = []
for s in samples:
if sum(s.x) == 3:
qaoa_res.append(("".join([str(int(_)) for _ in s.x]), s.fval, s.probability))
res = sorted(qaoa_res, key=lambda x: -x[1])[0:max_len]
return [(_[0] + f": value: {_[1]:.3f}, probability: {1e2*_[2]:.1f}%") for _ in res]
format_qaoa_samples(qaoa_result.samples)
[17]:
['001110: value: 16.769, probability: 0.7%',
'011010: value: 15.744, probability: 0.7%',
'001011: value: 14.671, probability: 0.6%',
'101010: value: 14.626, probability: 0.7%',
'010110: value: 14.234, probability: 2.3%',
'100110: value: 13.953, probability: 1.6%',
'000111: value: 13.349, probability: 1.5%',
'110010: value: 12.410, probability: 3.0%',
'010011: value: 12.013, probability: 2.7%',
'100011: value: 11.559, probability: 3.3%']
[18]:
format_qaoa_samples(ws_qaoa_result.samples)
[18]:
['001110: value: 16.769, probability: 72.8%',
'001011: value: 14.671, probability: 1.2%',
'101010: value: 14.626, probability: 2.6%',
'100110: value: 13.953, probability: 0.3%',
'000111: value: 13.349, probability: 0.1%',
'100011: value: 11.559, probability: 0.0%']
ウォーム・スタート QAOA#
上記の warm-start 機能は、下にある WarmStartQAOAOptimizer という名前の単一のオプティマイザーとして、Qiskit 最適化モジュールで利用可能です。このソルバーはウォーム・スタート QAOA で QUBO を解きます。それは問題を緩和することによって \(c^*\) を計算します。この動作は relax_for_pre_solver を True に設定することで制御できます。
[19]:
from qiskit_optimization.algorithms import WarmStartQAOAOptimizer
[20]:
qaoa_mes = QAOA(sampler=Sampler(), optimizer=COBYLA(), initial_point=[0.0, 1.0])
ws_qaoa = WarmStartQAOAOptimizer(
pre_solver=CplexOptimizer(), relax_for_pre_solver=True, qaoa=qaoa_mes, epsilon=0.0
)
[21]:
ws_result = ws_qaoa.solve(qubo)
print(ws_result.prettyprint())
objective function value: 16.768932200000002
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS
[22]:
format_qaoa_samples(ws_result.samples)
[22]:
['001110: value: 16.769, probability: 72.8%',
'001011: value: 14.671, probability: 1.2%',
'101010: value: 14.626, probability: 2.6%',
'100110: value: 13.953, probability: 0.3%',
'000111: value: 13.349, probability: 0.1%',
'100011: value: 11.559, probability: 0.0%']
[23]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Software | Version |
|---|---|
qiskit | 0.45.1 |
qiskit_algorithms | 0.2.1 |
qiskit_optimization | 0.7.0 |
| System information | |
| Python version | 3.10.13 |
| Python compiler | GCC 13.2.1 20230728 (Red Hat 13.2.1-1) |
| Python build | main, Aug 28 2023 00:00:00 |
| OS | Linux |
| CPUs | 12 |
| Memory (Gb) | 31.056411743164062 |
| Wed Dec 06 10:26:59 2023 CET | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: