注釈

このページは docs/tutorials/03_minimum_eigen_optimizer.ipynb から生成されました。

最小固有値オプティマイザー (Minimum Eigen Optimizer)#

はじめに#

量子コンピューティングを適用する最適化問題の興味深いクラスには、制約なし二次形式二値変換最適化 (Quadratic Unconstrained Binary Optimization、QUBO) 問題があります。QUBO の解を求めることは、対応するイジング・ハミルトニアンの基底状態を見つけることに相当します。これは最適化だけでなく、量子化学や量子物理学にも重要な問題です。この変換の場合、 \(\{0, 1\}\) の値を取るバイナリ変数は、 \(\{-1, +1\}\) の値を取るスピン変数に置き換えられます。これにより、パウリ Z 行列によって得られるスピン変数をイジング・ハミルトニアンに置換することができます。このマッピングの詳細については、[1]を参照してください。

Qiskit optimizationは、適切な QuadraticProgram からイジング・ハミルトニアンへの自動変換を提供します。これにより、次のようなすべての SamplingMinimumEigensolver を活用できます。

SamplingVQE,
QAOA 、または
NumpyMinimumEigensolver （古典的厳密法）。

注 1: MinimumEigenOptimizer は qiskit_algorithms.VQE をサポートしていません。しかし、代わりに qiskit_algorithms.SamplingVQE を使用できます。

注 2: NumpyMinimumEigensolver は、( SamplingMinimumEigensolver ではなく) MinimumEigensolver を継承していますが、MinimumEigenOptimizer はそれを例外ケースとして使用できます。

Qiskit optimization は、 MinimumEigenOptimizer クラスを提供します。これは、変換をイジングハミルトニアン（Qiskit Terra では SparsePauliOp とも呼ばれます）にラップし、 MinimumEigensolver を呼び出し、結果を OptimizationResult に変換します。

以下では、まず、QuadraticProgram から SparsePauliOp への変換を示します。次に、与えられた QuadraticProgram を解くのに、MinimumEigenOptimizer を異なる MinimumEigensolver にどう使うのかを示します。Qiskit optimizationのアルゴリズムは、与えられた問題を、可能であればサポートされている問題クラスに自動的に変換しようとします。例えば、MinimumEigenOptimizer は整数変数をバイナリー変数に自動的に変換したり、線形等価制約を2次ペナルティ項として目的関数に追加したりします。整数変数を持つ二次計画問題を変換しようとすると、 QiskitOptimizationError が投げられることに注意してください。

QAOA の回路の深さは、問題の大きさに応じて必然的に増加する可能性があり、これは近未来の量子デバイスにとっては障害となる可能性があります。考えられる回避策として、 [2] で紹介されている再帰QAOAがあります。このチュートリアルの最後で紹介しますが、Qiskit optimizationはこの概念を RecursiveMinimumEigenOptimizer に一般化しています。

参考文献#

[1] A. Lucas, Ising formulations of many NP problems, Front. Phys., 12 (2014).

[2] S. Bravyi, A. Kliesch, R. Koenig, E. Tang, Obstacles to State Preparation and Variational Optimization from Symmetry Protection, arXiv preprint arXiv:1910.08980 (2019).

QUBOをSparsePauliOpに変換する#

[1]:

from qiskit_algorithms.utils import algorithm_globals
from qiskit_algorithms import QAOA, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import COBYLA
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import (
    MinimumEigenOptimizer,
    RecursiveMinimumEigenOptimizer,
    SolutionSample,
    OptimizationResultStatus,
)
from qiskit_optimization import QuadraticProgram
from qiskit.visualization import plot_histogram
from typing import List, Tuple
import numpy as np

[2]:

# create a QUBO
qubo = QuadraticProgram()
qubo.binary_var("x")
qubo.binary_var("y")
qubo.binary_var("z")
qubo.minimize(linear=[1, -2, 3], quadratic={("x", "y"): 1, ("x", "z"): -1, ("y", "z"): 2})
print(qubo.prettyprint())

Problem name:

Minimize
  x*y - x*z + 2*y*z + x - 2*y + 3*z

Subject to
  No constraints

  Binary variables (3)
    x y z

次に、このQUBOをIsingオペレータに変換します。変換の結果は、SparsePauliOp だけではなく、結果の値をシフトするのに考慮すべき定数オフセットにもなります。

[3]:

op, offset = qubo.to_ising()
print("offset: {}".format(offset))
print("operator:")
print(op)

offset: 1.5
operator:
SparsePauliOp(['IIZ', 'IZI', 'ZII', 'IZZ', 'ZIZ', 'ZZI'],
              coeffs=[-0.5 +0.j,  0.25+0.j, -1.75+0.j,  0.25+0.j, -0.25+0.j,  0.5 +0.j])

ときには、QuadraticProgram が SparsePauliOp の形でも直接与えられる場合があります。このような場合、Qiskit optimizationは SparsePauliOp から QuadraticProgram に戻す変換機能を備えています。これについては以下で説明します。

[4]:

qp = QuadraticProgram()
qp.from_ising(op, offset, linear=True)
print(qp.prettyprint())

Problem name:

Minimize
  x0*x1 - x0*x2 + 2*x1*x2 + x0 - 2*x1 + 3*x2

Subject to
  No constraints

  Binary variables (3)
    x0 x1 x2

このコンバーターにより、例えば、SparsePauliOp を QuadraticProgram に変換して、イジング・ハミルトニアン表現に基づいていない他のアルゴリズム（例えば GroverOptimizer ）で問題を解くことができます。

MinimumEigenOptimizer で QUBO を解く#

まず、使用する MinimumEigensolver を初期化します。

[5]:

algorithm_globals.random_seed = 10598
qaoa_mes = QAOA(sampler=Sampler(), optimizer=COBYLA(), initial_point=[0.0, 0.0])
exact_mes = NumPyMinimumEigensolver()

次に、MinimumEigensolver を使用して MinimumEigenOptimizer を作成します。

[6]:

qaoa = MinimumEigenOptimizer(qaoa_mes)  # using QAOA
exact = MinimumEigenOptimizer(exact_mes)  # using the exact classical numpy minimum eigen solver

最初に、古典的で厳密な NumPyMinimumEigensolver に基づいた MinimumEigenOptimizer を使用して、この小さな例に対してベンチマークとなる最適解を求めます。

[7]:

exact_result = exact.solve(qubo)
print(exact_result.prettyprint())

objective function value: -2.0
variable values: x=0.0, y=1.0, z=0.0
status: SUCCESS

次に、同じ問題に対して、QAOA に基づいた MinimumEigenOptimizer を適用します。

[8]:

qaoa_result = qaoa.solve(qubo)
print(qaoa_result.prettyprint())

objective function value: -2.0
variable values: x=0.0, y=1.0, z=0.0
status: SUCCESS

サンプルの分析#

OptimizationResult は、 SolutionSample （ここでは samples と表記）の形式で有用な情報を提供します。各 SolutionSample には、入力値（ x ）、対応する目的関数値（ fval ）、その入力に対応するサンプルの割合（ probability ）、およびソリューションのステータス（ SUCCESS 、 FAILURE 、 INFEASIBLE ）に関する情報が含まれています。同じ入力に対応する複数のサンプルが単一の SolutionSample に統合されます（その probability 属性は、その SolutionSample によって表されるサンプルの総計です）。

[9]:

print("variable order:", [var.name for var in qaoa_result.variables])
for s in qaoa_result.samples:
    print(s)

variable order: ['x', 'y', 'z']
SolutionSample(x=array([0., 1., 0.]), fval=-2.0, probability=0.4409914383320322, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 0.]), fval=0.0, probability=0.2276808656506505, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 0.]), fval=0.0, probability=0.1413908468641879, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 0.]), fval=1.0, probability=0.1257339279014548, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 1.]), fval=3.0, probability=0.020491301242878, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 1.]), fval=3.0, probability=0.0304288193232328, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 1., 1.]), fval=3.0, probability=0.0123642766450843, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 1.]), fval=4.0, probability=0.0009185240404783, status=<OptimizationResultStatus.SUCCESS: 0>)

また、ステータスや確率によって、サンプルをフィルターすることもできます。

[10]:

def get_filtered_samples(
    samples: List[SolutionSample],
    threshold: float = 0,
    allowed_status: Tuple[OptimizationResultStatus] = (OptimizationResultStatus.SUCCESS,),
):
    res = []
    for s in samples:
        if s.status in allowed_status and s.probability > threshold:
            res.append(s)

    return res

[11]:

filtered_samples = get_filtered_samples(
    qaoa_result.samples, threshold=0.005, allowed_status=(OptimizationResultStatus.SUCCESS,)
)
for s in filtered_samples:
    print(s)

SolutionSample(x=array([0., 1., 0.]), fval=-2.0, probability=0.4409914383320322, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 0.]), fval=0.0, probability=0.2276808656506505, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 0.]), fval=0.0, probability=0.1413908468641879, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 0.]), fval=1.0, probability=0.1257339279014548, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 1.]), fval=3.0, probability=0.020491301242878, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 1.]), fval=3.0, probability=0.0304288193232328, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 1., 1.]), fval=3.0, probability=0.0123642766450843, status=<OptimizationResultStatus.SUCCESS: 0>)

もし結果のより良い全体像をみたければ、目的関数の値とそれぞれの確率に関して、統計が役立ちます。したがって、平均と標準偏差は結果を理解するための基本になります。

[12]:

fvals = [s.fval for s in qaoa_result.samples]
probabilities = [s.probability for s in qaoa_result.samples]

[13]:

np.mean(fvals)

[13]:

1.5

[14]:

np.std(fvals)

[14]:

1.9364916731037085

最後に、あらゆる数値処理を差し置いて、可視化は通常最適な早期分析アプローチです。

[15]:

samples_for_plot = {
    " ".join(f"{qaoa_result.variables[i].name}={int(v)}" for i, v in enumerate(s.x)): s.probability
    for s in filtered_samples
}
samples_for_plot

[15]:

{'x=0 y=1 z=0': 0.4409914383320322,
 'x=0 y=0 z=0': 0.2276808656506505,
 'x=1 y=1 z=0': 0.1413908468641879,
 'x=1 y=0 z=0': 0.1257339279014548,
 'x=0 y=0 z=1': 0.020491301242878,
 'x=1 y=0 z=1': 0.0304288193232328,
 'x=0 y=1 z=1': 0.0123642766450843}

[16]:

plot_histogram(samples_for_plot)

[16]:

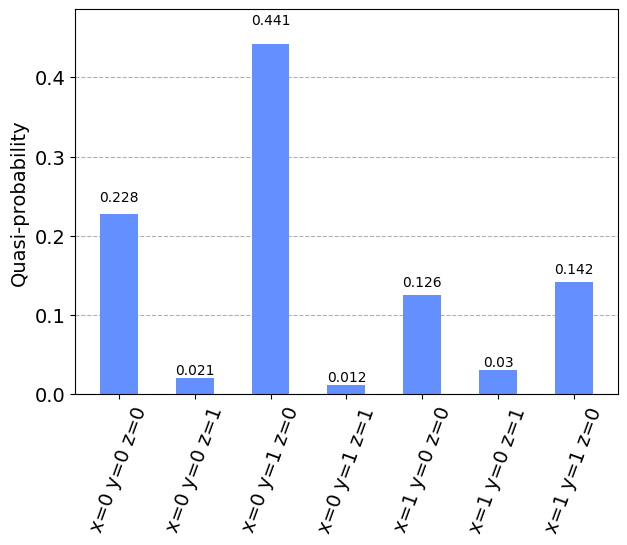
../_images/tutorials_03_minimum_eigen_optimizer_31_0.png

RecursiveMinimumEigenOptimizer#

RecursiveMinimumEigenOptimizer は入力として MinimumEigenOptimizer を取り、再帰的な最適化スキームを適用して、問題のサイズを一度に1変数ずつ小さくします。生成された中間問題のサイズが与えられたしきい値 (min_num_vars) を下回ると、RecursiveMinimumEigenOptimizer は別のソルバー(min_num_vars_optimizer)を使用します。（例えば NumPyMinimumEigensolver に基づく、CPLEXや MinimumEigenOptimizer などの厳密な古典ソルバーなど）

以下では、以前に導入した 2 つの MinimumEigenOptimizer を使用して RecursiveMinimumEigenOptimizer を使用する方法を示します。

最初に RecursiveMinimumEigenOptimizer を構築し、問題サイズを3つの変数から1つの変数に縮小し、最後の変数に正確なソルバーを使用します。次に、検討された問題を最適化するために solve を呼び出します。

[17]:

rqaoa = RecursiveMinimumEigenOptimizer(qaoa, min_num_vars=1, min_num_vars_optimizer=exact)

[18]:

rqaoa_result = rqaoa.solve(qubo)
print(rqaoa_result.prettyprint())

objective function value: -2.0
variable values: x=0.0, y=1.0, z=0.0
status: SUCCESS

[19]:

filtered_samples = get_filtered_samples(
    rqaoa_result.samples, threshold=0.005, allowed_status=(OptimizationResultStatus.SUCCESS,)
)

[20]:

samples_for_plot = {
    " ".join(f"{rqaoa_result.variables[i].name}={int(v)}" for i, v in enumerate(s.x)): s.probability
    for s in filtered_samples
}
samples_for_plot

[20]:

{'x=0 y=1 z=0': 1.0}

[21]:

plot_histogram(samples_for_plot)

[21]:

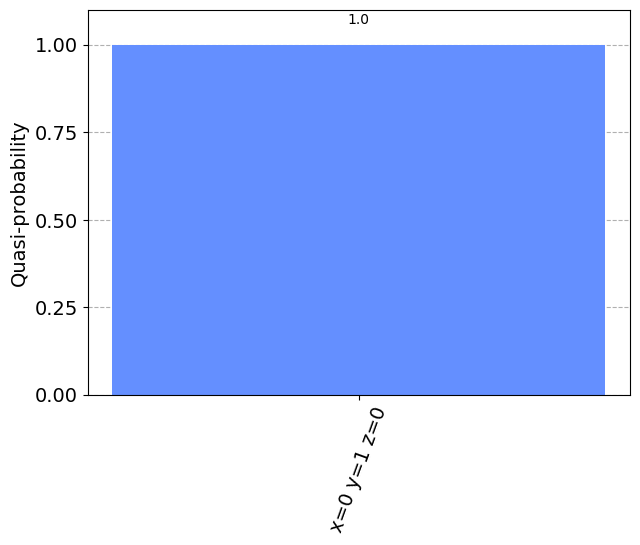
../_images/tutorials_03_minimum_eigen_optimizer_39_0.png

[22]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
`qiskit-terra`	0.25.0.dev0+1d844ec
`qiskit-aer`	0.12.0
`qiskit-ibmq-provider`	0.20.2
`qiskit-nature`	0.7.0
`qiskit-optimization`	0.6.0
System information
Python version	3.10.11
Python compiler	Clang 14.0.0 (clang-1400.0.29.202)
Python build	main, Apr 7 2023 07:31:31
OS	Darwin
CPUs	4
Memory (Gb)	16.0
Thu May 18 16:56:50 2023 JST

This code is a part of Qiskit

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.

[ ]: