CVaRを使用した変分量子最適化の改善#

はじめに#

このノートブックは、Qiskit Algorithms <https://qiskit.org/ecosystem/algorithms/>`__が提供する変分量子最適化アルゴリズム内で [1] で紹介されたConditional Value at Risk (CVaR) 目的関数を使用する方法を示しています。特に、 ``SamplingVQE` を使用して MinimumEigenOptimizer を設定する方法を示します。考慮される最適化問題に対応する客観的価値を持つショットの特定のセットについて、信頼水準 \(\alpha \in [0, 1]\) のCVaRは、 \(\alpha\) ベストショットの平均として定義されます。したがって、 \(\alpha = 1\) は標準の期待値に対応し、 \(\alpha=0\) は与えられたショットの最小値に対応し、 \(\alpha \in (0, 1)\) はより良いショットに焦点を合わせる間のトレードオフですが、最適化ランドスケープをスムーズにするために平均化を適用します。

参考文献#

[1] P. Barkoutsos et al., Improving Variational Quantum Optimization using CVaR, Quantum 4, 256 (2020).

[1]:

from qiskit.circuit.library import RealAmplitudes
from qiskit_algorithms.optimizers import COBYLA
from qiskit_algorithms import NumPyMinimumEigensolver, SamplingVQE
from qiskit_algorithms.utils import algorithm_globals
from qiskit.primitives import Sampler
from qiskit_optimization.converters import LinearEqualityToPenalty
from qiskit_optimization.algorithms import MinimumEigenOptimizer
from qiskit_optimization.translators import from_docplex_mp

import numpy as np
import matplotlib.pyplot as plt
from docplex.mp.model import Model

[2]:

algorithm_globals.random_seed = 123456

ポートフォリオの最適化#

以下では、 [1] で紹介したポートフォリオ最適化の問題インスタンスを定義します。

[3]:

# prepare problem instance
n = 6  # number of assets
q = 0.5  # risk factor
budget = n // 2  # budget
penalty = 2 * n  # scaling of penalty term

[4]:

# instance from [1]
mu = np.array([0.7313, 0.9893, 0.2725, 0.8750, 0.7667, 0.3622])
sigma = np.array(
    [
        [0.7312, -0.6233, 0.4689, -0.5452, -0.0082, -0.3809],
        [-0.6233, 2.4732, -0.7538, 2.4659, -0.0733, 0.8945],
        [0.4689, -0.7538, 1.1543, -1.4095, 0.0007, -0.4301],
        [-0.5452, 2.4659, -1.4095, 3.5067, 0.2012, 1.0922],
        [-0.0082, -0.0733, 0.0007, 0.2012, 0.6231, 0.1509],
        [-0.3809, 0.8945, -0.4301, 1.0922, 0.1509, 0.8992],
    ]
)

# or create random instance
# mu, sigma = portfolio.random_model(n, seed=123)  # expected returns and covariance matrix

[5]:

# create docplex model
mdl = Model("portfolio_optimization")
x = mdl.binary_var_list(range(n), name="x")
objective = mdl.sum([mu[i] * x[i] for i in range(n)])
objective -= q * mdl.sum([sigma[i, j] * x[i] * x[j] for i in range(n) for j in range(n)])
mdl.maximize(objective)
mdl.add_constraint(mdl.sum(x[i] for i in range(n)) == budget)

# case to
qp = from_docplex_mp(mdl)

[6]:

# solve classically as reference
opt_result = MinimumEigenOptimizer(NumPyMinimumEigensolver()).solve(qp)
print(opt_result.prettyprint())

objective function value: 1.27835
variable values: x_0=1.0, x_1=1.0, x_2=0.0, x_3=0.0, x_4=1.0, x_5=0.0
status: SUCCESS

[7]:

# we convert the problem to an unconstrained problem for further analysis,
# otherwise this would not be necessary as the MinimumEigenSolver would do this
# translation automatically
linear2penalty = LinearEqualityToPenalty(penalty=penalty)
qp = linear2penalty.convert(qp)
_, offset = qp.to_ising()

SamplingVQEを使用した最小固有オプティマイザー（Minimum Eigen Optimizer）#

[8]:

# set classical optimizer
maxiter = 100
optimizer = COBYLA(maxiter=maxiter)

# set variational ansatz
ansatz = RealAmplitudes(n, reps=1)
m = ansatz.num_parameters

# set sampler
sampler = Sampler()

# run variational optimization for different values of alpha
alphas = [1.0, 0.50, 0.25]  # confidence levels to be evaluated

[9]:

# dictionaries to store optimization progress and results
objectives = {alpha: [] for alpha in alphas}  # set of tested objective functions w.r.t. alpha
results = {}  # results of minimum eigensolver w.r.t alpha

# callback to store intermediate results
def callback(i, params, obj, stddev, alpha):
    # we translate the objective from the internal Ising representation
    # to the original optimization problem
    objectives[alpha].append(np.real_if_close(-(obj + offset)))


# loop over all given alpha values
for alpha in alphas:

    # initialize SamplingVQE using CVaR
    vqe = SamplingVQE(
        sampler=sampler,
        ansatz=ansatz,
        optimizer=optimizer,
        aggregation=alpha,
        callback=lambda i, params, obj, stddev: callback(i, params, obj, stddev, alpha),
    )

    # initialize optimization algorithm based on CVaR-SamplingVQE
    opt_alg = MinimumEigenOptimizer(vqe)

    # solve problem
    results[alpha] = opt_alg.solve(qp)

    # print results
    print("alpha = {}:".format(alpha))
    print(results[alpha].prettyprint())
    print()

alpha = 1.0:
objective function value: 1.2783500000000174
variable values: x_0=1.0, x_1=1.0, x_2=0.0, x_3=0.0, x_4=1.0, x_5=0.0
status: SUCCESS

alpha = 0.5:
objective function value: 1.2783500000000174
variable values: x_0=1.0, x_1=1.0, x_2=0.0, x_3=0.0, x_4=1.0, x_5=0.0
status: SUCCESS

alpha = 0.25:
objective function value: 1.2783500000000174
variable values: x_0=1.0, x_1=1.0, x_2=0.0, x_3=0.0, x_4=1.0, x_5=0.0
status: SUCCESS

[10]:

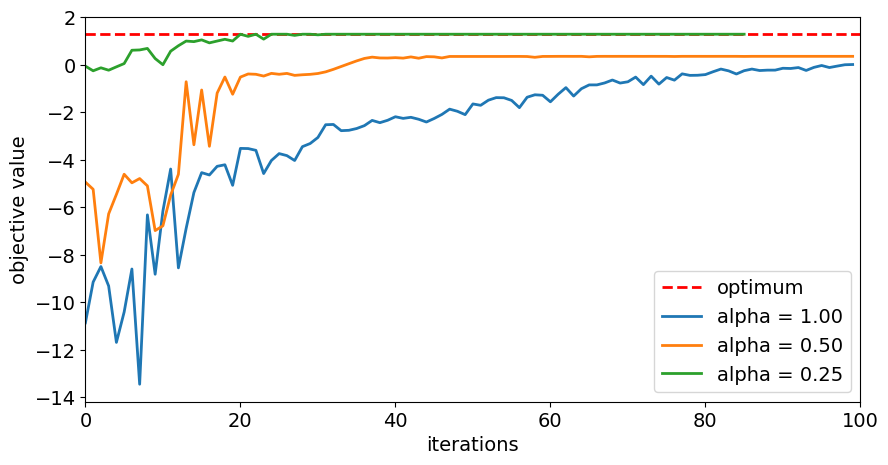
# plot resulting history of objective values
plt.figure(figsize=(10, 5))
plt.plot([0, maxiter], [opt_result.fval, opt_result.fval], "r--", linewidth=2, label="optimum")
for alpha in alphas:
    plt.plot(objectives[alpha], label="alpha = %.2f" % alpha, linewidth=2)
plt.legend(loc="lower right", fontsize=14)
plt.xlim(0, maxiter)
plt.xticks(fontsize=14)
plt.xlabel("iterations", fontsize=14)
plt.yticks(fontsize=14)
plt.ylabel("objective value", fontsize=14)
plt.show()

../_images/tutorials_08_cvar_optimization_13_0.png

[11]:

# evaluate and sort all objective values
objective_values = np.zeros(2**n)
for i in range(2**n):
    x_bin = ("{0:0%sb}" % n).format(i)
    x = [0 if x_ == "0" else 1 for x_ in reversed(x_bin)]
    objective_values[i] = qp.objective.evaluate(x)
ind = np.argsort(objective_values)

# evaluate final optimal probability for each alpha
for alpha in alphas:
    probabilities = np.fromiter(
        results[alpha].min_eigen_solver_result.eigenstate.binary_probabilities().values(),
        dtype=float,
    )
    print("optimal probability (alpha = %.2f):  %.4f" % (alpha, probabilities[ind][-1:]))

optimal probability (alpha = 1.00):  0.0000
optimal probability (alpha = 0.50):  0.0000
optimal probability (alpha = 0.25):  0.2895

[12]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
`qiskit-terra`	0.25.0.dev0+1d844ec
`qiskit-aer`	0.12.0
`qiskit-ibmq-provider`	0.20.2
`qiskit-nature`	0.7.0
`qiskit-optimization`	0.6.0
System information
Python version	3.10.11
Python compiler	Clang 14.0.0 (clang-1400.0.29.202)
Python build	main, Apr 7 2023 07:31:31
OS	Darwin
CPUs	4
Memory (Gb)	16.0
Thu May 18 16:56:49 2023 JST

This code is a part of Qiskit

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.

[ ]: