注釈

このページは `docs/tutorials/12_quantum_random_access_optimizer.ipynb`__ から生成されました。

量子ランダムアクセス最適化 (Quantum Random Access Optimization)

量子ランダムアクセス最適化（Quantum Random Access Optimization: QRAO）モジュールは、組合せ最適化問題[1] に新しい量子手法を活用できるように設計されています。この手法は、量子ランダムアクセスコード（Quantum Random Access Codes: QRAC）を、複数の古典的なバイナリ変数を1つの量子ビットにエンコードするツールとして組み込んだもので、これにより量子リソースを節約し、量子コンピューター上でより大規模な問題インスタンスを探索することが可能になります。この符号化により、局所的な量子ハミルトニアンが生成され、その基底状態はVQEなどの標準的なアルゴリズムで近似することができ、その後、元の問題の近似解を得るために丸められます。

QRAOは3つのクラスで構成されています: 1. 符号化クラス(QuantumRandomAccessEncoding): このクラスは元の問題を、解くのに必要なリソースがより少ない緩和された問題にエンコードします。 2. 丸めスキーム (SemideterministicRounding と MagicRounding): このスキームは、緩和された問題から得られた解を元の問題の解に丸めるために使用されます。 3. オプティマイザークラス(QuantumRandomAccessOptimizer): このクラスは、符号化クラスと丸めスキームの機能を利用して、高レベルの最適化アルゴリズムを実行します。

参考文献

[1] Bryce Fuller et al., Approximate Solutions of Combinatorial Problems via Quantum Relaxations, arXiv:2111.03167

from qiskit_optimization.algorithms.qrao import (
    QuantumRandomAccessEncoding,
    SemideterministicRounding,
    QuantumRandomAccessOptimizer,
)

組合せ最適化問題を設定する

このチュートリアルでは、ランダムなマックスカット問題のインスタンスを検討し、QRAO を使用して最大カットを見つけようとします。 言い換えれば、グラフの頂点 (ノード) を 2 つのセットに分割し、セット間のエッジの数を最大化します。

はじめに、Qiskit Optimizationのアプリケーションモジュールにある Maxcut クラスを利用します。これにより、与えられたグラフの QuadraticProgram 表現を生成することができます。

問題が QuadraticProgram として表現されたら、QRAOと互換性があるように、正しい型である 二次制約なし二項最適化（QUBO） 問題に変換する必要があることに注意してください。 Maxcut によって生成された``QuadraticProgram`` はすでにQUBOですが、もし自分で問題を定義する場合には、先に進む前に必ずQUBOに変換してください。 QuadraticPrograms の変換についての チュートリアルはこちら です。

import networkx as nx

from qiskit_optimization.applications import Maxcut

seed = 1
num_nodes = 6
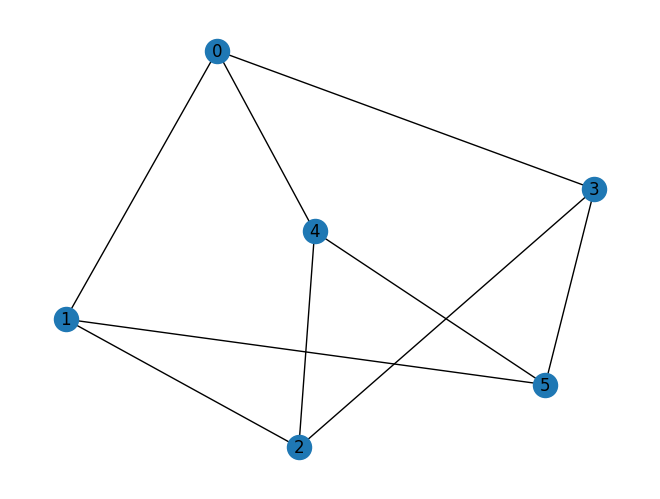
graph = nx.random_regular_graph(d=3, n=num_nodes, seed=seed)
nx.draw(graph, with_labels=True, pos=nx.spring_layout(graph, seed=seed))

maxcut = Maxcut(graph)
problem = maxcut.to_quadratic_program()
print(problem.prettyprint())

Problem name: Max-cut

Maximize
  -2*x_0*x_1 - 2*x_0*x_3 - 2*x_0*x_4 - 2*x_1*x_2 - 2*x_1*x_5 - 2*x_2*x_3
  - 2*x_2*x_4 - 2*x_3*x_5 - 2*x_4*x_5 + 3*x_0 + 3*x_1 + 3*x_2 + 3*x_3 + 3*x_4
  + 3*x_5

Subject to
  No constraints

  Binary variables (6)
    x_0 x_1 x_2 x_3 x_4 x_5

量子ハミルトニアンに問題を符号化する

問題を適切に設定したら、 qrao モジュールの QuantumRandomAccessEncoding クラスを使って符号化します。この符号化ステップによって、問題を表す量子ハミルトニアン演算子を生成することができます。特に、量子ランダムアクセスコード(QRAC) を用いて、複数の古典バイナリ変数(マックスカットグラフのノードに対応) を各量子ビットにエンコードします。

この符号化によって生成される 「relaxed」 ハミルトニアンは対角ではないことに注意することが重要です。これは 通常は MinimumEigenOptimizer を使った最適化に適した対角（Ising）ハミルトニアンを生成する qiskit-optimization の標準的なワークフローとは異なります。 MinimumEigenOptimizer の `チュートリアルはこちら<https://qiskit.org/documentation/optimization/tutorials/03_minimum_eigen_optimizer.html>`__ です。

私たちの符号化プロセスでは、 \((3,1,p)-\)QRAC を採用しており、各量子ビットは最大 3 つの古典的なバイナリ変数に対応できます。 パラメータ \(p\) は、測定によって得られたビット回復確率を表します。 問題の性質によっては、一部の量子ビットに割り当てられている古典的な変数が 3 つ未満である場合があります。 達成された圧縮を評価するには、符号化の compression_ratio 属性を調べることができます。これは、元のバイナリ変数の数と使用される量子ビットの数の間の比率 (最大で 3 の係数) を提供します。

from qiskit_optimization.algorithms.qrao import QuantumRandomAccessEncoding


# Create an encoding object with a maximum of 3 variables per qubit, aka a (3,1,p)-QRAC
encoding = QuantumRandomAccessEncoding(max_vars_per_qubit=3)

# Encode the QUBO problem into an encoded Hamiltonian
encoding.encode(problem)

# This is our encoded Hamiltonian
print(f"Our encoded Hamiltonian is:\n( {encoding.qubit_op} ).\n")
print(
    "We achieve a compression ratio of "
    f"({encoding.num_vars} binary variables : {encoding.num_qubits} qubits) "
    f"≈ {encoding.compression_ratio}.\n"
)

Our encoded Hamiltonian is:
( SparsePauliOp(['XX', 'XY', 'XZ', 'YX', 'ZX', 'YY', 'YZ', 'ZY', 'ZZ'],
              coeffs=[1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j,
 1.5+0.j]) ).

We achieve a compression ratio of (6 binary variables : 2 qubits) ≈ 3.0.

QuantumRandomAccessOptimizer を使って問題を解く

入力問題を緩和されたハミルトニアンとして符号化することに成功したので、 QuantumRandomAccessOptimizer を使って解を求めます。このオプティマイザーは、量子計算技術を活用することで、緩和された問題の近似解を求めることができます。

オプティマイザーを設定するには、2つの重要なコンポーネントを指定する必要があります：

1. 最小固有値解法: 緩和問題のハミルトニアンの基底状態を発見的に探索する最小固有値解法を指定します。例として、変分量子固有値ソルバー(VQE) を使うことができます。シミュレーションのために、シミュレーターを使用しますが、必要であればバックエンドに量子デバイスを選択することもできます。

2. 丸めスキーム: 基底状態の結果を元の問題の解に戻すために、丸めスキームを指定します。デフォルトでは SemideterministicRounding が使用されますが、 MagicRounding も使用できます。

from qiskit_algorithms import VQE
from qiskit_algorithms.optimizers import COBYLA
from qiskit.circuit.library import RealAmplitudes
from qiskit.primitives import Estimator

from qiskit_optimization.algorithms.qrao import (
    QuantumRandomAccessOptimizer,
    SemideterministicRounding,
)


# Prepare the VQE algorithm
ansatz = RealAmplitudes(2)
vqe = VQE(
    ansatz=ansatz,
    optimizer=COBYLA(),
    estimator=Estimator(),
)

# Use semi-deterministic rounding, known as "Pauli rounding"
# in https://arxiv.org/pdf/2111.03167v2.pdf
# (This is the default if no rounding scheme is specified.)
semidterministic_rounding = SemideterministicRounding()

# Construct the optimizer
qrao = QuantumRandomAccessOptimizer(min_eigen_solver=vqe, rounding_scheme=semidterministic_rounding)

最後に、 solve() メソッドを呼び出して問題を解きます。 solve() を呼び出すときに、 problem そのものを引数として渡すことに注意することが重要です。以前は QuantumRandomAccessEncoding の encode() を使って流れを明確に理解していましたが、 solve(problem) は自動的に QuantumRandomAccessEncoding を使って問題を内部的に符号化します。これにより、明示的な符号化手順が不要になり、合理的で簡素化されたワークフローが実現します。

結果は QuantumRandomAccessOptimizationResult として提供されます。 x には、見つかった最適解を表すバイナリ値が格納され、 fval には対応する目的値が格納されます。

relaxed_fval は、元の最適化問題の単位になるように調整された緩和ハミルトニアンの期待値を提供します。最大化問題では、可能な限り最良の緩和された関数値は、常に元の問題の可能な限り最良の目的関数値以上となります。実際には、これは最良の発見値と最良の発見された目的関数値にも当てはまることが多いです。

# Solve the optimization problem
results = qrao.solve(problem)

print(
    f"The objective function value: {results.fval}\n"
    f"x: {results.x}\n"
    f"relaxed function value: {-1 * results.relaxed_fval}\n"
)

The objective function value: 6.0
x: [1 0 1 1 0 1]
relaxed function value: 8.999999989772657

解の解釈

max-cut の文脈では、結果の 「最適値」 は、オプティマイザーによって発見されたパーティションが与えられたときに、各ノードがどのサブセットに属するかを教えてくれます。

maxcut_partition = maxcut.interpret(results)
print(
    f"The obtained solution places a partition between nodes {maxcut_partition[0]} "
    f"and nodes {maxcut_partition[1]}."
)
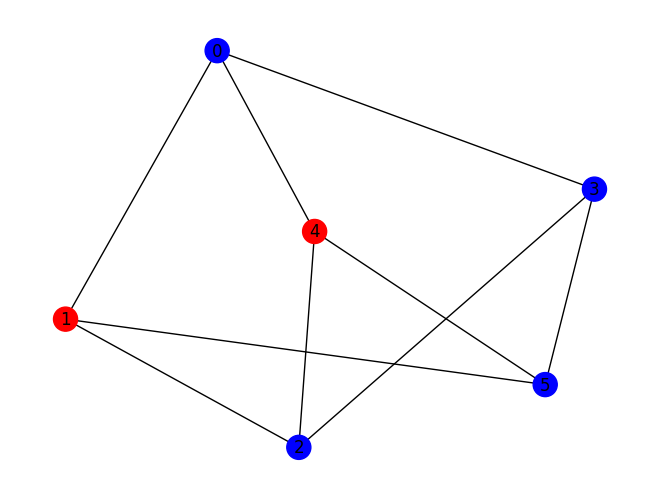
maxcut.draw(results, pos=nx.spring_layout(graph, seed=seed))

The obtained solution places a partition between nodes [1, 4] and nodes [0, 2, 3, 5].

サブルーチンの結果の検査

緩和されたハミルトニアンに対してVQEを実行した結果の MinimumEigensolverResult が利用できます：

results.relaxed_result

<qiskit_algorithms.minimum_eigensolvers.vqe.VQEResult at 0x1478add00>

丸めスキームの結果も検討に値します.。この例では、 SemideterministricRounding を使用しました。ここで重要なのは、半決定論的な丸め（semi-deterministic rounding）では、結果として1つのサンプルが生成され、それが最適解候補となることです。

しかし、代わりに MagicRounding を使用すると、複数のサンプルが生成され、それぞれに確率が関連付けられます。これらの確率の合計は1になり、最適解候補の分布が得られます。

results.samples

[SolutionSample(x=array([1, 0, 1, 1, 0, 1]), fval=6.0, probability=1.0, status=<OptimizationResultStatus.SUCCESS: 0>)]

NumpyMinimumEigensolver による問題の厳密解

最適解を近似するQRAOの性能を評価するために、厳密な古典的オプティマイザーである NumpyMinimumEigensolver を利用することができます。この問題の厳密最適解は次のように得られます：

from qiskit_algorithms import NumPyMinimumEigensolver

from qiskit_optimization.algorithms import MinimumEigenOptimizer

exact_mes = NumPyMinimumEigensolver()
exact = MinimumEigenOptimizer(exact_mes)
exact_result = exact.solve(problem)
print(exact_result.prettyprint())

objective function value: 9.0
variable values: x_0=0.0, x_1=1.0, x_2=0.0, x_3=1.0, x_4=1.0, x_5=0.0
status: SUCCESS

近似比（QRAOの目的関数値を最適目的関数値で割った値）は、QRAOが問題の最適解にどれだけ近づいたかを示しています。

print("QRAO Approximate Optimal Function Value:", results.fval)
print("Exact Optimal Function Value:", exact_result.fval)
print(f"Approximation Ratio: {results.fval /  exact_result.fval :.2f}")

QRAO Approximate Optimal Function Value: 6.0
Exact Optimal Function Value: 9.0
Approximation Ratio: 0.67

QuantumRandomAccessOptimizer と MagicRounding を使って問題を解く

Magic rounding は、符号化されたハミルトニアンの基底状態の結果を元の問題の解にマップするために採用される量子テクニックです。半決定論的丸め（semi-deterministic rounding）とは異なり、Magic rounding には量子バックエンドが必要であり、ハードウェアでもシミュレーターでもよいです。このバックエンドは Sampler を通して MagicRounding クラスに渡され、この Sampler が Magic rounding が利用するショット（サンプル）の総数を決定します。バックエンドを指定するには、AerやIBM Runtimeなどのプロバイダーから Sampler を選択する必要があることに注意してください。その結果、オプティマイザーには Estimator を、丸め方式には Sampler をそれぞれ指定する必要があります。

実際には、緩和された問題に対して最小固有値解法が使用するショット数と比較して、magic roundingのショット数を大幅に多く設定することがあります。この違いは、最小固有値ソルバーが期待値を推定するのに対して、magic rounding スキームは発見された最大関数値に対応するサンプルを返すことから生じます。magic rounding のショット数は、生成できる計算基底の多様性に直接影響します。期待値を推定する場合、ショット数を増やすと真の値への収束が向上します。しかし、可能な限り大きな関数値を特定することを目的とする場合、結果の分布の末尾からサンプリングすることがよくあります。その結果、分布の中で最高値の結果を観察するまでは、ショットを追加するごとに期待値が増加します。

このチュートリアルでは、緩和されたハミルトニアンを解くために Estimator を使用し、magic rounding を実行するために Sampler を使用します。ここで、 Sampler では10倍のショットを使用します。量子ビット数が増加するにつれて、上記で説明したように、より多くのショットや weighted 基底サンプリングが必要になるかもしれません。

from qiskit.primitives import Sampler

from qiskit_optimization.algorithms.qrao import MagicRounding


estimator = Estimator(options={"shots": 1000, "seed": seed})
sampler = Sampler(options={"shots": 10000, "seed": seed})

# Prepare the VQE algorithm
ansatz = RealAmplitudes(2)
vqe = VQE(
    ansatz=ansatz,
    optimizer=COBYLA(),
    estimator=estimator,
)


# Use magic rounding
magic_rounding = MagicRounding(sampler=sampler)

# Construct the optimizer
qrao = QuantumRandomAccessOptimizer(min_eigen_solver=vqe, rounding_scheme=magic_rounding)

results = qrao.solve(problem)

print(
    f"The objective function value: {results.fval}\n"
    f"x: {results.x}\n"
    f"relaxed function value: {-1 * results.relaxed_fval}\n"
)

The objective function value: 9.0
x: [1 0 1 0 0 1]
relaxed function value: 8.999996519407159

Magic rounding は非決定的な測定に依存するため、このメソッドは、前述の Sampler に提供されたショット数に基づいて、いくつかのサンプルを収集します。これらのサンプルは、重複を考慮して統合され、各 SolutionSample の経験確率が計算されます。連結プロセスの各サンプルには、対応する関数値 (fval) が含まれます。

連結されたサンプルから、「最適な」関数値を持つサンプルを選択します。max-cut 問題の場合、これは最大の関数値を持つサンプルを解として選択することを意味します。

print(f"The number of distinct samples is {len(results.samples)}.")
print("Top 10 samples with the largest fval:")
for sample in results.samples[:10]:
    print(sample)

The number of distinct samples is 56.
Top 10 samples with the largest fval:
SolutionSample(x=array([1, 0, 1, 0, 0, 1]), fval=9.0, probability=0.0094, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0, 1, 0, 1, 1, 0]), fval=9.0, probability=0.0112, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0, 0, 0, 1, 1, 0]), fval=6.0, probability=0.0195, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1, 1, 1, 0, 0, 1]), fval=6.0, probability=0.0205, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0, 1, 1, 1, 1, 0]), fval=6.0, probability=0.0214, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1, 0, 0, 0, 0, 1]), fval=6.0, probability=0.0194, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1, 0, 1, 0, 0, 0]), fval=6.0, probability=0.0204, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0, 1, 0, 1, 1, 1]), fval=6.0, probability=0.021599999999999998, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1, 0, 1, 0, 1, 1]), fval=6.0, probability=0.02, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0, 1, 0, 1, 0, 0]), fval=6.0, probability=0.021, status=<OptimizationResultStatus.SUCCESS: 0>)

別の方法：2つの明示的なステップで問題を解く

このチュートリアルの前のパートでは、 qrao.solve() メソッドを利用し、符号化された問題（緩和ハミルトニアンの基底状態）を解き、基底状態の結果を元の問題の解に戻すために丸めを行いました。しかし、計算をこの2つの異なるステップに明確に分けることも可能です。これは、特に基底状態の候補に適用される複数の丸めスキームで得られた解を比較する場合に有益です。

このセクションでは、これらの各ステップを明示的に実行する方法を探ります。

手動で緩和問題を解く

まず、 qrao.solve_relaxed() メソッドを呼び出して、 QuantumRandomAccessEncoding で符号化された緩和問題を直接解くことから始めましょう。このメソッドにより、丸めを行わずに緩和問題を解くことだけに集中することができます。

qrao.solve_relaxed() を呼び出すことで、2つの重要な出力が得られます：

• MinimumEigensolverResult: このオブジェクトは、緩和された問題に対してVQEなどの最小固有値オプティマイザーを実行した結果を含みます。固有値やその他の関連する詳細についての情報を提供します。このオブジェクト内の項目の包括的な説明については、Qiskit Algorithmsの documentation を参照してください。

• RoundingContext: このオブジェクトは符号化と緩和問題の解に関する重要な情報を、丸めスキームがすぐに利用できる形でカプセル化します。

# Encode the QUBO problem into a relaxed Hamiltonian
encoding = QuantumRandomAccessEncoding(max_vars_per_qubit=3)
encoding.encode(problem)

# Solve the relaxed problem
relaxed_results, rounding_context = qrao.solve_relaxed(encoding)

for k in dir(relaxed_results):
    if not k.startswith("_"):
        print(f"{k}: {getattr(relaxed_results, k)}")

aux_operators_evaluated: [(0.010835872623325702, {'variance': 0.9999999914513272, 'shots': 1000}), (0.026074300411246972, {'variance': 0.999999991452347, 'shots': 1000}), (0.01044933784106082, {'variance': 1.0, 'shots': 1000}), (-0.04120945001189341, {'variance': 1.0, 'shots': 1000}), (0.02868127134978543, {'variance': 0.9999999973575187, 'shots': 1000}), (0.014064208211884945, {'variance': 0.9999999973585384, 'shots': 1000})]
combine: <bound method AlgorithmResult.combine of <qiskit_algorithms.minimum_eigensolvers.vqe.VQEResult object at 0x14789b880>>
cost_function_evals: 114
eigenvalue: -4.499994593889271
optimal_circuit:      ┌──────────────────────────────────────────────────────────┐
q_0: ┤0                                                         ├
     │  RealAmplitudes(θ[0],θ[1],θ[2],θ[3],θ[4],θ[5],θ[6],θ[7]) │
q_1: ┤1                                                         ├
     └──────────────────────────────────────────────────────────┘
optimal_parameters: {ParameterVectorElement(θ[0]): 0.3782657558818425, ParameterVectorElement(θ[1]): 2.6307309944567154, ParameterVectorElement(θ[2]): -1.872906908815765, ParameterVectorElement(θ[3]): 0.1989998525444124, ParameterVectorElement(θ[4]): -2.8660234975739094, ParameterVectorElement(θ[5]): -0.9853046968649906, ParameterVectorElement(θ[6]): -0.7699284547923341, ParameterVectorElement(θ[7]): 3.5498132912316986}
optimal_point: [ 0.37826576  2.63073099 -1.87290691  0.19899985 -2.8660235  -0.9853047
 -0.76992845  3.54981329]
optimal_value: -4.499994593889271
optimizer_evals: None
optimizer_result: {   'fun': -4.499994593889271,
    'jac': None,
    'nfev': 114,
    'nit': None,
    'njev': None,
    'x': array([ 0.37826576,  2.63073099, -1.87290691,  0.19899985, -2.8660235 ,
       -0.9853047 , -0.76992845,  3.54981329])}
optimizer_time: 0.19381928443908691

緩和問題の結果に対して手動で丸めを行う

次に、緩和問題を解いて得られた結果の丸めを行います。これを実現するために、希望する丸めスキームのインスタンスで round() メソッドを呼び出し、 RoundingContext オブジェクトを渡します。以下では、前のステップで得られた緩和解を使用して、両方の丸めスキームの例を示します。

丸めステップを手動で実行することで、緩和された問題の結果に適用される丸めスキームをより柔軟に制御することができます。これにより、様々な丸め方についてより深く検討し、比較することができます。

# Round the relaxed solution using semi-deterministic rounding
semidterministic_rounding = SemideterministicRounding()
sdr_results = semidterministic_rounding.round(rounding_context)
qrao_results_sdr = qrao.process_result(
    problem=problem, encoding=encoding, relaxed_result=relaxed_results, rounding_result=sdr_results
)

print(
    f"The objective function value: {qrao_results_sdr.fval}\n"
    f"x: {qrao_results_sdr.x}\n"
    f"relaxed function value: {-1 * qrao_results_sdr.relaxed_fval}\n"
    f"The number of distinct samples is {len(qrao_results_sdr.samples)}."
)

The objective function value: 3.0
x: [0 0 0 1 0 0]
relaxed function value: -8.999994593889271
The number of distinct samples is 1.

magic_rounding = MagicRounding(sampler=sampler)
mr_results = magic_rounding.round(rounding_context)
qrao_results_mr = qrao.process_result(
    problem=problem, encoding=encoding, relaxed_result=relaxed_results, rounding_result=mr_results
)

print(
    f"The objective function value: {qrao_results_mr.fval}\n"
    f"x: {qrao_results_mr.x}\n"
    f"relaxed function value: {-1 * qrao_results_mr.relaxed_fval}\n"
    f"The number of distinct samples is {len(qrao_results_mr.samples)}."
)

The objective function value: 9.0
x: [1 0 1 0 0 1]
relaxed function value: -8.999994593889271
The number of distinct samples is 56.

付録

符号化の正しさを検証する方法

QRAO法のために、 緩和が目的関数と交換関係にあること を仮定します。このノートブックは、どのような問題（Qiskit Optimizationの言語における QuadraticProgram ）においても、この仮定を検証する方法を示しています。教育目的や、QRAOの予期せぬ動作を調査する際の整合性チェックとして、これを検証したい場合があります。もし交換関係にない場合はバグとみなされる問題であり、もしそのような問題が発見された場合は、 GitHubにissueとして提出する ことをお勧めします。

EncodingCommutationVerifier クラスを使えば、すべての決定変数の状態を繰り返し、各目的値を対応する符号化された目的値と比較し、矛盾を特定することができます。

from qiskit_optimization.algorithms.qrao import EncodingCommutationVerifier

seed = 1
num_nodes = 6
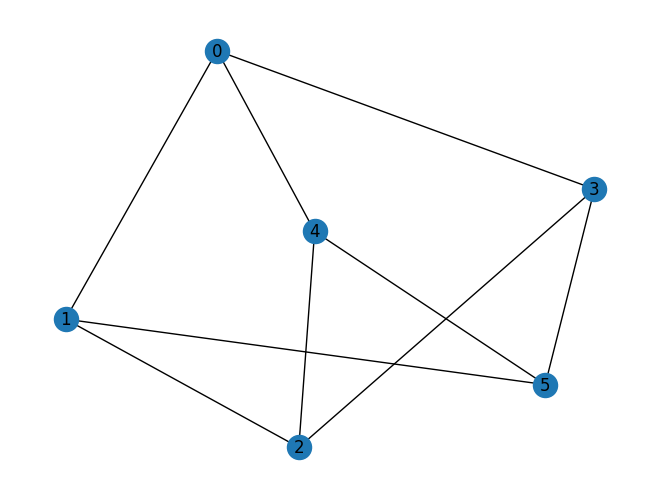
graph = nx.random_regular_graph(d=3, n=num_nodes, seed=seed)
nx.draw(graph, with_labels=True, pos=nx.spring_layout(graph, seed=seed))

maxcut = Maxcut(graph)
problem = maxcut.to_quadratic_program()
print(problem.prettyprint())

Problem name: Max-cut

Maximize
  -2*x_0*x_1 - 2*x_0*x_3 - 2*x_0*x_4 - 2*x_1*x_2 - 2*x_1*x_5 - 2*x_2*x_3
  - 2*x_2*x_4 - 2*x_3*x_5 - 2*x_4*x_5 + 3*x_0 + 3*x_1 + 3*x_2 + 3*x_3 + 3*x_4
  + 3*x_5

Subject to
  No constraints

  Binary variables (6)
    x_0 x_1 x_2 x_3 x_4 x_5

前回と同様に、QuantumRandomAccessEncoding クラスを使って問題を encode() します：

encoding = QuantumRandomAccessEncoding(max_vars_per_qubit=3)
encoding.encode(problem)

print("Encoded Problem:\n=================")
print(encoding.qubit_op)  # The Hamiltonian without the offset
print("Offset = ", encoding.offset)
print("Variables encoded on each qubit: ", encoding.q2vars)

Encoded Problem:
=================
SparsePauliOp(['XX', 'XY', 'XZ', 'YX', 'ZX', 'YY', 'YZ', 'ZY', 'ZZ'],
              coeffs=[1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j,
 1.5+0.j])
Offset =  -4.5
Variables encoded on each qubit:  [[0, 2, 5], [1, 3, 4]]

最後に、 EncodingCommutationVerifier を使ってすべての決定変数の状態を繰り返し、それぞれのケースで問題の目的値が符号化された目的値と一致することを検証します：

import numpy as np

verifier = EncodingCommutationVerifier(encoding, estimator=Estimator())
if not len(verifier) == 2**encoding.num_vars:
    print("The number results of the encoded problem is not equal to 2 ** num_vars.")

for str_dvars, obj_val, encoded_obj_val in verifier:
    if not np.isclose(obj_val, encoded_obj_val):
        print(
            f"Violation identified: {str_dvars} evaluates to {obj_val} "
            f"but the encoded problem evaluates to {encoded_obj_val}."
        )

違反が発生する問題を構築できた場合、QuantumRandomAccessEncoding のロジックにバグを発見した可能性が十分にあります。その問題を GitHubに issueとして提出する ことで、私たちと共有していただけると大変ありがたいです。

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
qiskit-terra	0.24.0.dev0+8a52d88
qiskit-aer	0.12.0
qiskit-optimization	0.6.0
System information
Python version	3.9.10
Python compiler	Clang 13.1.6 (clang-1316.0.21.2.5)
Python build	main, Aug 9 2022 18:26:17
OS	Darwin
CPUs	10
Memory (Gb)	64.0
Thu Sep 07 21:53:47 2023 JST

This code is a part of Qiskit

© Copyright IBM 2017, 2023.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.