Nota

Esta página fue generada a partir de docs/tutorials/12_quantum_random_access_optimizer.ipynb.

Optimización Cuántica de Acceso Aleatorio

El módulo Quantum Random Access Optimization (QRAO) está diseñado para permitir a los usuarios aprovechar un nuevo método cuántico para problemas de optimización combinatoria [1]. Este enfoque incorpora Códigos Cuánticos de Acceso Aleatorio (Quantum Random Access Codes, QRAC) como herramienta para codificar múltiples variables binarias clásicas en un solo qubit, ahorrando así recursos cuánticos y permitiendo la exploración de instancias de problemas más grandes en una computadora cuántica. Las codificaciones producen un Hamiltoniano cuántico local cuyo estado fundamental puede aproximarse con algoritmos estándar como VQE y luego redondearse para producir soluciones aproximadas del problema original.

QRAO a través de una serie de 3 clases: 1. La clase de codificación (QuantumRandomAccessEncoding): esta clase codifica el problema original en un problema relajado que requiere menos recursos para resolver. 2. Los esquemas de redondeo (SemidterministicRounding y MagicRounding): Este esquema se utiliza para redondear la solución obtenida del problema relajado a una solución del problema original. 3. La clase optimizadora (QuantumRandomAccessOptimizer): esta clase realiza el algoritmo de optimización de alto nivel, utilizando las capacidades de la clase de codificación y el esquema de redondeo.

Referencias

[1] Bryce Fuller et al., Approximate Solutions of Combinatorial Problems via Quantum Relaxations, arXiv:2111.03167

from qiskit_optimization.algorithms.qrao import (
    QuantumRandomAccessEncoding,
    SemideterministicRounding,
    QuantumRandomAccessOptimizer,
)

Configurar un problema de optimización combinatoria

En este tutorial, consideraremos una instancia de problema max-cut aleatorio y usaremos QRAO para intentar encontrar un corte máximo; en otras palabras, una partición de los vértices (nodos) del grafo en dos conjuntos que maximiza el número de aristas entre los conjuntos.

Para comenzar, utilizamos la clase Maxcut del módulo de aplicación de Qiskit Optimization. Nos permite generar una representación QuadraticProgram del grafo dado.

Ten en cuenta que una vez que nuestro problema se haya representado como un QuadraticProgram, será necesario convertirlo al tipo correcto, un problema de optimización binaria cuadrática sin restricciones (QUBO), para que sea compatible con QRAO. Un QuadraticProgram generado por Maxcut ya es un QUBO, pero si defines tu propio problema, asegúrate de convertirlo en un QUBO antes de continuar. Aquí hay un tutorial sobre la conversión de QuadraticPrograms.

import networkx as nx

from qiskit_optimization.applications import Maxcut

seed = 1
num_nodes = 6
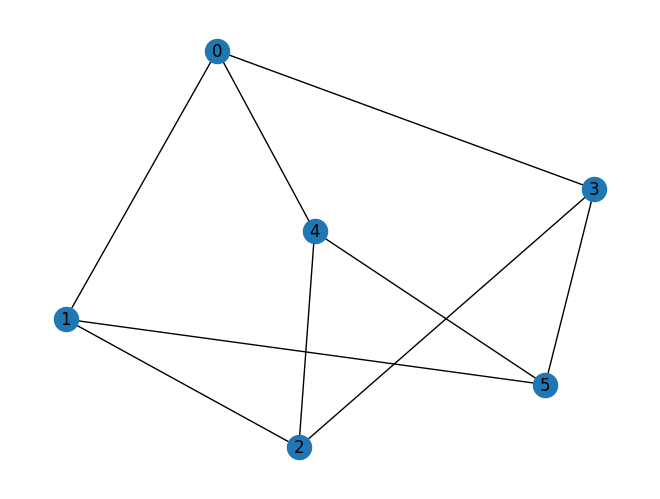
graph = nx.random_regular_graph(d=3, n=num_nodes, seed=seed)
nx.draw(graph, with_labels=True, pos=nx.spring_layout(graph, seed=seed))

maxcut = Maxcut(graph)
problem = maxcut.to_quadratic_program()
print(problem.prettyprint())

Problem name: Max-cut

Maximize
  -2*x_0*x_1 - 2*x_0*x_3 - 2*x_0*x_4 - 2*x_1*x_2 - 2*x_1*x_5 - 2*x_2*x_3
  - 2*x_2*x_4 - 2*x_3*x_5 - 2*x_4*x_5 + 3*x_0 + 3*x_1 + 3*x_2 + 3*x_3 + 3*x_4
  + 3*x_5

Subject to
  No constraints

  Binary variables (6)
    x_0 x_1 x_2 x_3 x_4 x_5

Codificar el problema en un Hamiltoniano cuántico

Una vez que hemos configurado adecuadamente nuestro problema, procedemos a codificarlo usando la clase QuantumRandomAccessEncoding del módulo qrao. Este paso de codificación nos permite generar un operador Hamiltoniano cuántico que representa nuestro problema. En particular, empleamos un código cuántico de acceso aleatorio (QRAC) para codificar múltiples variables binarias clásicas (correspondientes a los nodos de nuestro grafo max-cut) en cada qubit.

Es importante señalar que el Hamiltoniano «relajado» resultante, producido por esta codificación, no será diagonal. Esto difiere del flujo de trabajo estándar en qiskit-optimization, que normalmente genera un Hamiltoniano diagonal (Ising) adecuado para la optimización utilizando un MinimumEigenOptimizer. Puedes encontrar un tutorial sobre MinimumEigenOptimizer aquí.

En nuestro proceso de codificación, empleamos un \((3,1,p)-\)QRAC, donde cada qubit puede acomodar un máximo de 3 variables binarias clásicas. El parámetro \(p\) representa la probabilidad de recuperación de bits lograda mediante la medición. Dependiendo de la naturaleza del problema, algunos qubits pueden tener asignadas menos de 3 variables clásicas. Para evaluar la compresión lograda, podemos examinar el atributo compression_ratio de la codificación, que proporciona la relación entre el número de variables binarias originales y el número de qubits utilizados (en el mejor de los casos, un factor de 3).

from qiskit_optimization.algorithms.qrao import QuantumRandomAccessEncoding


# Create an encoding object with a maximum of 3 variables per qubit, aka a (3,1,p)-QRAC
encoding = QuantumRandomAccessEncoding(max_vars_per_qubit=3)

# Encode the QUBO problem into an encoded Hamiltonian
encoding.encode(problem)

# This is our encoded Hamiltonian
print(f"Our encoded Hamiltonian is:\n( {encoding.qubit_op} ).\n")
print(
    "We achieve a compression ratio of "
    f"({encoding.num_vars} binary variables : {encoding.num_qubits} qubits) "
    f"≈ {encoding.compression_ratio}.\n"
)

Our encoded Hamiltonian is:
( SparsePauliOp(['XX', 'XY', 'XZ', 'YX', 'ZX', 'YY', 'YZ', 'ZY', 'ZZ'],
              coeffs=[1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j,
 1.5+0.j]) ).

We achieve a compression ratio of (6 binary variables : 2 qubits) ≈ 3.0.

Resolver el problema usando el QuantumRandomAccessOptimizer

Habiendo codificado con éxito nuestro problema de entrada como un Hamiltoniano relajado, procedemos a resolverlo usando el QuantumRandomAccessOptimizer. Este optimizador nos permite encontrar una solución aproximada al problema relajado aprovechando técnicas de computación cuántica.

Para configurar el optimizador, necesitamos especificar dos componentes cruciales:

1. Solucionador Propio Mínimo: Especificamos un solucionador propio mínimo para buscar heurísticamente el estado fundamental del problema de Hamiltoniano relajado. Como ejemplo, podemos utilizar el Solucionador Propio Variacional Cuántico (Variational Quantum Eigensolver, VQE). Para fines de simulación, emplearemos un simulador, pero puedes elegir un dispositivo cuántico como backend si lo deseas.

2. Esquema de Redondeo: Para asignar los resultados del estado fundamental a una solución para el problema original, especificamos un esquema de redondeo. De forma predeterminada, se utiliza el SemideterministicRounding, pero también está disponible el esquema alternativo, MagicRounding.

from qiskit_algorithms import VQE
from qiskit_algorithms.optimizers import COBYLA
from qiskit.circuit.library import RealAmplitudes
from qiskit.primitives import Estimator

from qiskit_optimization.algorithms.qrao import (
    QuantumRandomAccessOptimizer,
    SemideterministicRounding,
)


# Prepare the VQE algorithm
ansatz = RealAmplitudes(2)
vqe = VQE(
    ansatz=ansatz,
    optimizer=COBYLA(),
    estimator=Estimator(),
)

# Use semi-deterministic rounding, known as "Pauli rounding"
# in https://arxiv.org/pdf/2111.03167v2.pdf
# (This is the default if no rounding scheme is specified.)
semidterministic_rounding = SemideterministicRounding()

# Construct the optimizer
qrao = QuantumRandomAccessOptimizer(min_eigen_solver=vqe, rounding_scheme=semidterministic_rounding)

Finalmente, avanzamos en la resolución del problema invocando el método solve(). Es importante tener en cuenta que cuando llamamos a solve(), pasamos el problem mismo como argumento. Aunque anteriormente usamos encode() en QuantumRandomAccessEncoding para proporcionar una comprensión clara del flujo, solve(problem) codifica automáticamente el problema internamente usando QuantumRandomAccessEncoding. Esto proporciona un flujo de trabajo optimizado y simplificado que elimina la necesidad de pasos de codificación explícitos.

El resultado se nos proporciona como QuantumRandomAccessOptimizationResult. La x contiene los valores binarios que representan la mejor solución encontrada, mientras que el fval contiene el valor objetivo correspondiente.

El relaxed_fval proporciona el valor esperado del Hamiltoniano relajado, ajustado para estar en las unidades del problema de optimización original. Para problemas de maximización, el mejor valor posible de la función relajada siempre será mayor o igual al mejor valor posible de la función objetivo del problema original. En la práctica, esto suele ser válido también para el mejor valor encontrado y el mejor valor de la función objetivo encontrado.

# Solve the optimization problem
results = qrao.solve(problem)

print(
    f"The objective function value: {results.fval}\n"
    f"x: {results.x}\n"
    f"relaxed function value: {-1 * results.relaxed_fval}\n"
)

The objective function value: 6.0
x: [1 0 1 1 0 1]
relaxed function value: 8.999999989772657

Interpretar la solución

En el contexto de max-cut, el «valor óptimo» del resultado nos dice a qué subconjunto pertenece cada nodo dada la partición encontrada por el optimizador.

maxcut_partition = maxcut.interpret(results)
print(
    f"The obtained solution places a partition between nodes {maxcut_partition[0]} "
    f"and nodes {maxcut_partition[1]}."
)
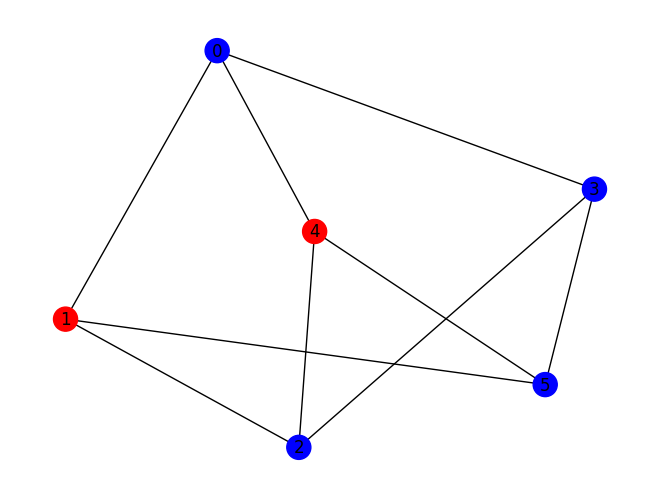
maxcut.draw(results, pos=nx.spring_layout(graph, seed=seed))

The obtained solution places a partition between nodes [1, 4] and nodes [0, 2, 3, 5].

Inspeccionar los resultados de las subrutinas

El MinimumEigensolverResult que resulta de aplicar VQE en el Hamiltoniano relajado está disponible:

results.relaxed_result

<qiskit_algorithms.minimum_eigensolvers.vqe.VQEResult at 0x1478add00>

También vale la pena considerar el resultado del esquema de redondeo. En este ejemplo, utilizamos el SemideterministricRounding. Es importante tener en cuenta que con el redondeo semideterminista, se genera una única muestra como resultado, lo que la convierte en la solución candidata óptima.

Sin embargo, si utilizamos MagicRounding en su lugar, se generarían múltiples muestras, cada una con una probabilidad asociada. Estas probabilidades suman uno, lo que proporciona una distribución de posibles soluciones óptimas.

results.samples

[SolutionSample(x=array([1, 0, 1, 1, 0, 1]), fval=6.0, probability=1.0, status=<OptimizationResultStatus.SUCCESS: 0>)]

Solución Exacta del Problema con NumpyMinimumEigensolver

Para evaluar el rendimiento de QRAO en la aproximación de la solución óptima, podemos utilizar NumpyMinimumEigensolver, un optimizador clásico exacto. Podemos obtener la solución óptima exacta del problema de la siguiente manera:

from qiskit_algorithms import NumPyMinimumEigensolver

from qiskit_optimization.algorithms import MinimumEigenOptimizer

exact_mes = NumPyMinimumEigensolver()
exact = MinimumEigenOptimizer(exact_mes)
exact_result = exact.solve(problem)
print(exact_result.prettyprint())

objective function value: 9.0
variable values: x_0=0.0, x_1=1.0, x_2=0.0, x_3=1.0, x_4=1.0, x_5=0.0
status: SUCCESS

La relación de aproximación (el valor de la función objetivo de QRAO dividido por el valor de la función objetivo óptima) nos dice qué tan cerca se aproximó QRAO a la solución óptima del problema.

print("QRAO Approximate Optimal Function Value:", results.fval)
print("Exact Optimal Function Value:", exact_result.fval)
print(f"Approximation Ratio: {results.fval /  exact_result.fval :.2f}")

QRAO Approximate Optimal Function Value: 6.0
Exact Optimal Function Value: 9.0
Approximation Ratio: 0.67

Resolver el problema usando el QuantumRandomAccessOptimizer con MagicRounding

El redondeo mágico es una técnica cuántica empleada para mapear los resultados del estado fundamental de nuestro Hamiltoniano codificado hasta una solución del problema original. A diferencia del redondeo semideterminista, el redondeo mágico requiere un backend cuántico, que puede ser hardware o un simulador. El backend se pasa a la clase MagicRounding a través de un Sampler, que también determina el número total de iteraciones (muestras) que utilizará el redondeo mágico. Ten en cuenta que para especificar el backend, debes elegir un Sampler de proveedores como Aer o IBM Runtime. En consecuencia, necesitamos especificar Estimador y Sampler para el optimizador y el esquema de redondeo, respectivamente.

En la práctica, los usuarios pueden optar por establecer un número significativamente mayor de iteraciones de redondeo mágico en comparación con los disparos utilizados por el solucionador propio mínimo para el problema relajado. Esta diferencia surge porque el solucionador propio mínimo estima los valores esperados, mientras que el esquema de redondeo mágico devuelve la muestra correspondiente al valor máximo de función encontrado. La cantidad de iteraciones de redondeo mágico impacta directamente en la diversidad de la base computacional que podemos generar. Al estimar un valor esperado, aumentar el número de iteraciones mejora la convergencia al valor real. Sin embargo, cuando pretendemos identificar el valor de función más grande posible, a menudo tomamos muestras de la cola de una distribución de resultados. Como resultado, hasta que observemos la salida de mayor valor en nuestra distribución, cada iteración adicional aumenta el valor de retorno esperado.

En este tutorial, utilizamos el Estimator para resolver el Hamiltoniano relajado y el Sampler para realizar el redondeo mágico. Aquí se utilizan 10 veces más iteraciones en el Sampler. A medida que aumenta el número de qubits, es posible que necesites más iteraciones o muestreos de base``weighted``, como se explicó anteriormente.

from qiskit.primitives import Sampler

from qiskit_optimization.algorithms.qrao import MagicRounding


estimator = Estimator(options={"shots": 1000, "seed": seed})
sampler = Sampler(options={"shots": 10000, "seed": seed})

# Prepare the VQE algorithm
ansatz = RealAmplitudes(2)
vqe = VQE(
    ansatz=ansatz,
    optimizer=COBYLA(),
    estimator=estimator,
)


# Use magic rounding
magic_rounding = MagicRounding(sampler=sampler)

# Construct the optimizer
qrao = QuantumRandomAccessOptimizer(min_eigen_solver=vqe, rounding_scheme=magic_rounding)

results = qrao.solve(problem)

print(
    f"The objective function value: {results.fval}\n"
    f"x: {results.x}\n"
    f"relaxed function value: {-1 * results.relaxed_fval}\n"
)

The objective function value: 9.0
x: [1 0 1 0 0 1]
relaxed function value: 8.999996519407159

Dado que el redondeo mágico se basa en mediciones no deterministas, el método recopila una cantidad de muestras en función del recuento de iteraciones proporcionado al Sampler mencionado anteriormente. Luego, estas muestras se consolidan, teniendo en cuenta los duplicados y calculando la probabilidad empírica para cada SolutionSample. Cada muestra en el proceso de consolidación incluye un valor de función correspondiente (fval).

De las muestras consolidadas, seleccionamos la muestra con el valor de función «óptimo». En el caso de un problema de máximo corte, esto significa elegir la muestra con el valor de función más grande como nuestra solución.

print(f"The number of distinct samples is {len(results.samples)}.")
print("Top 10 samples with the largest fval:")
for sample in results.samples[:10]:
    print(sample)

The number of distinct samples is 56.
Top 10 samples with the largest fval:
SolutionSample(x=array([1, 0, 1, 0, 0, 1]), fval=9.0, probability=0.0094, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0, 1, 0, 1, 1, 0]), fval=9.0, probability=0.0112, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0, 0, 0, 1, 1, 0]), fval=6.0, probability=0.0195, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1, 1, 1, 0, 0, 1]), fval=6.0, probability=0.0205, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0, 1, 1, 1, 1, 0]), fval=6.0, probability=0.0214, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1, 0, 0, 0, 0, 1]), fval=6.0, probability=0.0194, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1, 0, 1, 0, 0, 0]), fval=6.0, probability=0.0204, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0, 1, 0, 1, 1, 1]), fval=6.0, probability=0.021599999999999998, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1, 0, 1, 0, 1, 1]), fval=6.0, probability=0.02, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0, 1, 0, 1, 0, 0]), fval=6.0, probability=0.021, status=<OptimizationResultStatus.SUCCESS: 0>)

Alternativa: Resolver el Problema en dos Pasos Explícitos

En la parte anterior de este tutorial, utilizamos el método qrao.solve(), que resolvió el problema codificado (el estado fundamental del Hamiltoniano relajado) y realizamos un redondeo para mapear los resultados del estado fundamental a una solución del problema original. Sin embargo, también es posible dividir explícitamente el cálculo en estos dos pasos distintos. Esto puede resultar beneficioso, especialmente al comparar soluciones obtenidas a través de múltiples esquemas de redondeo aplicados a un estado fundamental candidato.

En esta sección, exploraremos cómo realizar cada uno de estos pasos de forma explícita.

Resuelve manualmente el problema relajado.

Comencemos invocando al método qrao.solve_relaxed() para resolver directamente el problema relajado codificado por QuantumRandomAccessEncoding. Este método nos permite centrarnos únicamente en resolver el problema relajado sin realizar redondeo.

Al invocar qrao.solve_relaxed(), obtenemos dos salidas esenciales:

• MinimumEigensolverResult: este objeto contiene los resultados de ejecutar el optimizador propio mínimo, como el VQE, en el problema relajado. Proporciona información sobre el valor propio y otros detalles relevantes. Puedes consultar la documentación de Qiskit Algorithms para obtener una explicación completa de las entradas dentro de este objeto.

• RoundingContext: este objeto encapsula información esencial sobre la codificación y la solución del problema relajado en una forma que esté lista para ser consumida por los esquemas de redondeo.

# Encode the QUBO problem into a relaxed Hamiltonian
encoding = QuantumRandomAccessEncoding(max_vars_per_qubit=3)
encoding.encode(problem)

# Solve the relaxed problem
relaxed_results, rounding_context = qrao.solve_relaxed(encoding)

for k in dir(relaxed_results):
    if not k.startswith("_"):
        print(f"{k}: {getattr(relaxed_results, k)}")

aux_operators_evaluated: [(0.010835872623325702, {'variance': 0.9999999914513272, 'shots': 1000}), (0.026074300411246972, {'variance': 0.999999991452347, 'shots': 1000}), (0.01044933784106082, {'variance': 1.0, 'shots': 1000}), (-0.04120945001189341, {'variance': 1.0, 'shots': 1000}), (0.02868127134978543, {'variance': 0.9999999973575187, 'shots': 1000}), (0.014064208211884945, {'variance': 0.9999999973585384, 'shots': 1000})]
combine: <bound method AlgorithmResult.combine of <qiskit_algorithms.minimum_eigensolvers.vqe.VQEResult object at 0x14789b880>>
cost_function_evals: 114
eigenvalue: -4.499994593889271
optimal_circuit:      ┌──────────────────────────────────────────────────────────┐
q_0: ┤0                                                         ├
     │  RealAmplitudes(θ[0],θ[1],θ[2],θ[3],θ[4],θ[5],θ[6],θ[7]) │
q_1: ┤1                                                         ├
     └──────────────────────────────────────────────────────────┘
optimal_parameters: {ParameterVectorElement(θ[0]): 0.3782657558818425, ParameterVectorElement(θ[1]): 2.6307309944567154, ParameterVectorElement(θ[2]): -1.872906908815765, ParameterVectorElement(θ[3]): 0.1989998525444124, ParameterVectorElement(θ[4]): -2.8660234975739094, ParameterVectorElement(θ[5]): -0.9853046968649906, ParameterVectorElement(θ[6]): -0.7699284547923341, ParameterVectorElement(θ[7]): 3.5498132912316986}
optimal_point: [ 0.37826576  2.63073099 -1.87290691  0.19899985 -2.8660235  -0.9853047
 -0.76992845  3.54981329]
optimal_value: -4.499994593889271
optimizer_evals: None
optimizer_result: {   'fun': -4.499994593889271,
    'jac': None,
    'nfev': 114,
    'nit': None,
    'njev': None,
    'x': array([ 0.37826576,  2.63073099, -1.87290691,  0.19899985, -2.8660235 ,
       -0.9853047 , -0.76992845,  3.54981329])}
optimizer_time: 0.19381928443908691

Realiza manualmente el redondeo de los resultados del problema relajado

Luego, se procede a redondear los resultados obtenidos al resolver el problema relajado. Para lograr esto, llamamos al método round() en una instancia del esquema de redondeo deseado y le pasamos el objeto RoundingContext. A continuación, proporcionamos un ejemplo para ambos esquemas de redondeo, utilizando la solución relajada obtenida en el paso anterior.

Al realizar manualmente el paso de redondeo, tenemos más flexibilidad y control sobre el esquema de redondeo aplicado a los resultados relajados del problema. Esto permite una mayor exploración y comparación de diferentes estrategias de redondeo.

# Round the relaxed solution using semi-deterministic rounding
semidterministic_rounding = SemideterministicRounding()
sdr_results = semidterministic_rounding.round(rounding_context)
qrao_results_sdr = qrao.process_result(
    problem=problem, encoding=encoding, relaxed_result=relaxed_results, rounding_result=sdr_results
)

print(
    f"The objective function value: {qrao_results_sdr.fval}\n"
    f"x: {qrao_results_sdr.x}\n"
    f"relaxed function value: {-1 * qrao_results_sdr.relaxed_fval}\n"
    f"The number of distinct samples is {len(qrao_results_sdr.samples)}."
)

The objective function value: 3.0
x: [0 0 0 1 0 0]
relaxed function value: -8.999994593889271
The number of distinct samples is 1.

magic_rounding = MagicRounding(sampler=sampler)
mr_results = magic_rounding.round(rounding_context)
qrao_results_mr = qrao.process_result(
    problem=problem, encoding=encoding, relaxed_result=relaxed_results, rounding_result=mr_results
)

print(
    f"The objective function value: {qrao_results_mr.fval}\n"
    f"x: {qrao_results_mr.x}\n"
    f"relaxed function value: {-1 * qrao_results_mr.relaxed_fval}\n"
    f"The number of distinct samples is {len(qrao_results_mr.samples)}."
)

The objective function value: 9.0
x: [1 0 1 0 0 1]
relaxed function value: -8.999994593889271
The number of distinct samples is 56.

Apéndice

Cómo verificar la exactitud de tu codificación

Por el método QRAO, asumimos que la relajación conmuta con la función objetivo. Este cuaderno demuestra cómo se puede verificar esto para cualquier problema (un QuadraticProgram en el lenguaje de Qiskit Optimization). Es posible que desees verificar esto con fines pedagógicos o como punto de control al investigar un comportamiento inesperado con el QRAO. Cualquier problema que no conmute debe considerarse un error y, si se descubre dicho problema, te recomendamos que lo envíes como un problema en GitHub.

La clase EncodingCommutationVerifier permite iterar convenientemente sobre todos los estados de las variables de decisión y comparar cada valor objetivo con el valor objetivo codificado correspondiente, para identificar cualquier discrepancia.

from qiskit_optimization.algorithms.qrao import EncodingCommutationVerifier

seed = 1
num_nodes = 6
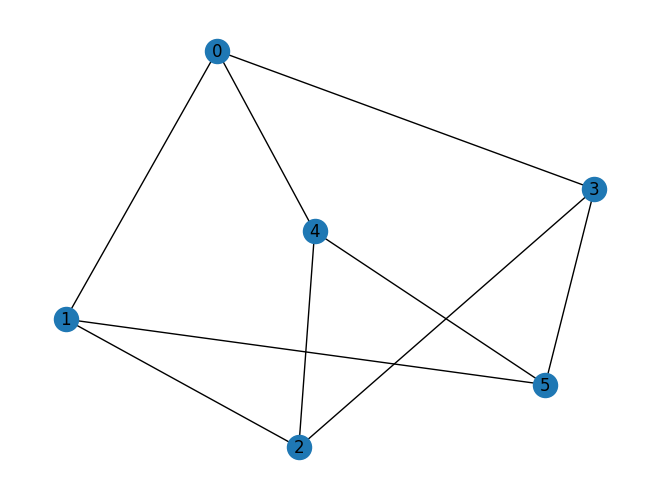
graph = nx.random_regular_graph(d=3, n=num_nodes, seed=seed)
nx.draw(graph, with_labels=True, pos=nx.spring_layout(graph, seed=seed))

maxcut = Maxcut(graph)
problem = maxcut.to_quadratic_program()
print(problem.prettyprint())

Problem name: Max-cut

Maximize
  -2*x_0*x_1 - 2*x_0*x_3 - 2*x_0*x_4 - 2*x_1*x_2 - 2*x_1*x_5 - 2*x_2*x_3
  - 2*x_2*x_4 - 2*x_3*x_5 - 2*x_4*x_5 + 3*x_0 + 3*x_1 + 3*x_2 + 3*x_3 + 3*x_4
  + 3*x_5

Subject to
  No constraints

  Binary variables (6)
    x_0 x_1 x_2 x_3 x_4 x_5

Como antes, encode() el problema usando la clase QuantumRandomAccessEncoding:

encoding = QuantumRandomAccessEncoding(max_vars_per_qubit=3)
encoding.encode(problem)

print("Encoded Problem:\n=================")
print(encoding.qubit_op)  # The Hamiltonian without the offset
print("Offset = ", encoding.offset)
print("Variables encoded on each qubit: ", encoding.q2vars)

Encoded Problem:
=================
SparsePauliOp(['XX', 'XY', 'XZ', 'YX', 'ZX', 'YY', 'YZ', 'ZY', 'ZZ'],
              coeffs=[1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j, 1.5+0.j,
 1.5+0.j])
Offset =  -4.5
Variables encoded on each qubit:  [[0, 2, 5], [1, 3, 4]]

Finalmente, iteramos sobre cada estado de variable de decisión usando EncodingCommutationVerifier y verificamos que, en cada caso, el valor objetivo del problema coincida con el valor objetivo codificado:

import numpy as np

verifier = EncodingCommutationVerifier(encoding, estimator=Estimator())
if not len(verifier) == 2**encoding.num_vars:
    print("The number results of the encoded problem is not equal to 2 ** num_vars.")

for str_dvars, obj_val, encoded_obj_val in verifier:
    if not np.isclose(obj_val, encoded_obj_val):
        print(
            f"Violation identified: {str_dvars} evaluates to {obj_val} "
            f"but the encoded problem evaluates to {encoded_obj_val}."
        )

Si puedes crear un problema que cause una infracción, es muy posible que hayas descubierto un error en la lógica de QuantumRandomAccessEncoding. Te agradeceríamos mucho si pudieras compartir el problema con nosotros enviándolo como un problema en GitHub.

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
qiskit-terra	0.24.0.dev0+8a52d88
qiskit-aer	0.12.0
qiskit-optimization	0.6.0
System information
Python version	3.9.10
Python compiler	Clang 13.1.6 (clang-1316.0.21.2.5)
Python build	main, Aug 9 2022 18:26:17
OS	Darwin
CPUs	10
Memory (Gb)	64.0
Thu Sep 07 21:53:47 2023 JST

This code is a part of Qiskit

© Copyright IBM 2017, 2023.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.