Nota

Esta página fue generada a partir de docs/tutorials/04_grover_optimizer.ipynb.

Optimizador de Grover

Introducción

La Búsqueda Adaptativa de Grover (Grover Adaptive Search, GAS) ha sido explorada como una posible solución para problemas de optimización combinatoria, junto con los algoritmos variacionales tal como el Solucionador Propio Cuántico Variacional (Variational Quantum Eigensolver, VQE) y el Algoritmo Cuántico de Optimización Aproximada (Quantum Approximate Optimization Algorithm, QAOA). El algoritmo aplica la Búsqueda de Grover iterativamente para encontrar el valor óptimo de una función objetivo, al usar el mejor valor conocido de la ejecución anterior como umbral. El oráculo adaptativo utilizado en GAS reconoce todos los valores arriba o debajo del umbral actual (para máximos y mínimos, respectivamente), disminuyendo el tamaño del espacio de búsqueda, en cada iteración se actualiza el umbral, hasta que se encuentra un óptimo.

En este cuaderno exploraremos cada componente del GroverOptimizer, el cual utiliza las técnicas descritas en GAS, minimizando un problema de Optimización Binaria Cuadrática sin Restricciones (Quadratic Unconstrained Binary Optimization, QUBO), como se describe en [1]

Referencias

[1] A. Gilliam, S. Woerner, C. Gonciulea, Grover Adaptive Search for Constrained Polynomial Binary Optimization, arXiv preprint arXiv:1912.04088 (2019).

Búsqueda Adaptativa de Grover

La Búsqueda de Grover, el elemento central de GAS, necesita de tres ingredientes:

1. Un operador de preparación de estado \(A\) para construir una superposición de todos los estados en el espacio de búsqueda.

2. Un operador oráculo \(O\), que reconoce a los estados de interés y multiplica sus amplitudes por -1.

3. El operador de difusión de Grover \(D\), que multiplica la amplitud del estado \(|0\rangle_n\) por -1.

Si bien las implementaciones de GAS varían según el caso de uso específico, el framework general aún sigue vagamente los pasos que se describen a continuación.

GroverOptimizer utiliza QuadraticProgramToNegativeValueOracle para construir \(A_y\) de manera que prepara un registro de \(n\) qubits para representar la superposición igual de todos los \(|x\rangle_n\) y un registro de \(m\) qubits para representar (aproximadamente) el correspondiente \(|Q(x)-y\rangle_m\). Entonces, todos los estados con una \((Q(x) - y)\) negativa deben ser marcados con \(O_y\). Ten en cuenta que en la implementación discutida, el operador oráculo es en realidad independiente de \(y\), pero esto no es un requisito. Para mayor claridad, nos referiremos al oráculo como \(O\) cuando el oráculo es independiente de \(y\).

Dicho formalmente, QuadraticProgramToNegativeValueOracle construye un \(A_y\) y un \(O\) tal que:

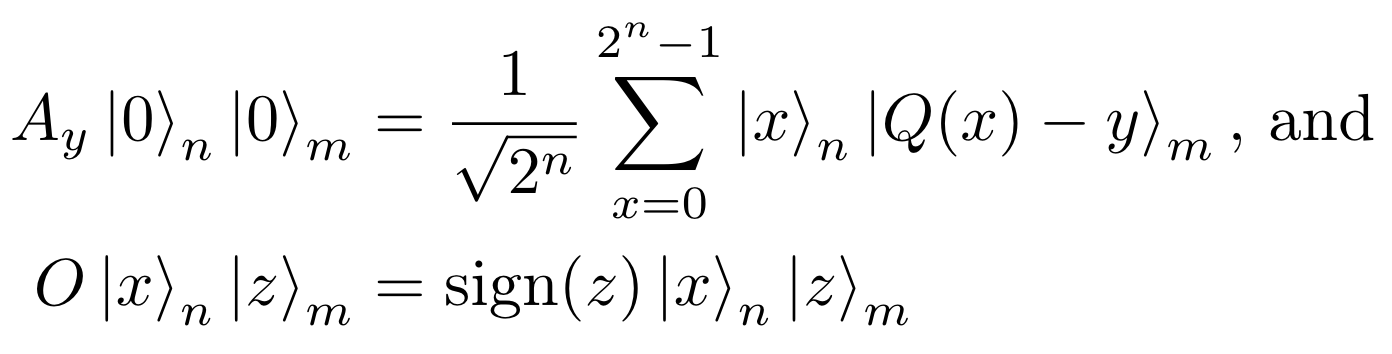
donde \(|x\rangle\) es la codificación binaria del entero \(x\).

En cada iteración en la que se actualiza el umbral \(y\), adaptamos \(A_y\) de manera que los valores de la función se desplazan hacia arriba o hacia abajo (para el mínimo y el máximo respectivamente) por \(y\). Por ejemplo, en el contexto de encontrar el mínimo, a medida que el valor de \(y\) disminuye, el espacio de búsqueda (valores negativos) también disminuye, hasta que solo queda el valor mínimo. Se explorará un ejemplo concreto en la siguiente sección.

Encontrar el Mínimo de un Problema QUBO utilizando GroverOptimizer

El siguiente es un ejemplo de juguete de un problema de minimización.

\begin{eqnarray} \min_{x \in \{0, 1\}^3} -2x_0x_2 - x_1x_2 - 1x_0 + 2x_1 - 3x_2. \end{eqnarray}

Para nuestros pasos iniciales, creamos un modelo docplex que define el problema anterior, y luego usamos la función from_docplex_mp() para convertir el modelo en un QuadraticProgram, que se puede usar para representar un QUBO en Qiskit Optimization.

from qiskit_algorithms import NumPyMinimumEigensolver
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import GroverOptimizer, MinimumEigenOptimizer
from qiskit_optimization.translators import from_docplex_mp
from docplex.mp.model import Model

model = Model()
x0 = model.binary_var(name="x0")
x1 = model.binary_var(name="x1")
x2 = model.binary_var(name="x2")
model.minimize(-x0 + 2 * x1 - 3 * x2 - 2 * x0 * x2 - 1 * x1 * x2)
qp = from_docplex_mp(model)
print(qp.prettyprint())

Problem name: docplex_model1

Minimize
  -2*x0*x2 - x1*x2 - x0 + 2*x1 - 3*x2

Subject to
  No constraints

  Binary variables (3)
    x0 x1 x2

A continuación, creamos un GroverOptimizer que usa 6 qubits para codificar el valor y terminará después de que haya habido 10 iteraciones de GAS sin progreso (es decir, el valor de \(y\) no cambia). La función solve() toma el QuadraticProgram que creamos anteriormente y devuelve un objeto de resultados que contiene información sobre la ejecución.

grover_optimizer = GroverOptimizer(6, num_iterations=10, sampler=Sampler())
results = grover_optimizer.solve(qp)
print(results.prettyprint())

objective function value: -6.0
variable values: x0=1.0, x1=0.0, x2=1.0
status: SUCCESS

Esto resulta en la solución óptima \(x_0=1\), \(x_1=0\), \(x_2=1\) y el valor objetivo óptimo de \(-6\) (la mayoría del tiempo, ya que es un algoritmo randomizado). A continuación, una visualización personalisada del estado cuántico muestra una posible ejecución de GroverOptimizer aplicada a este QUBO.

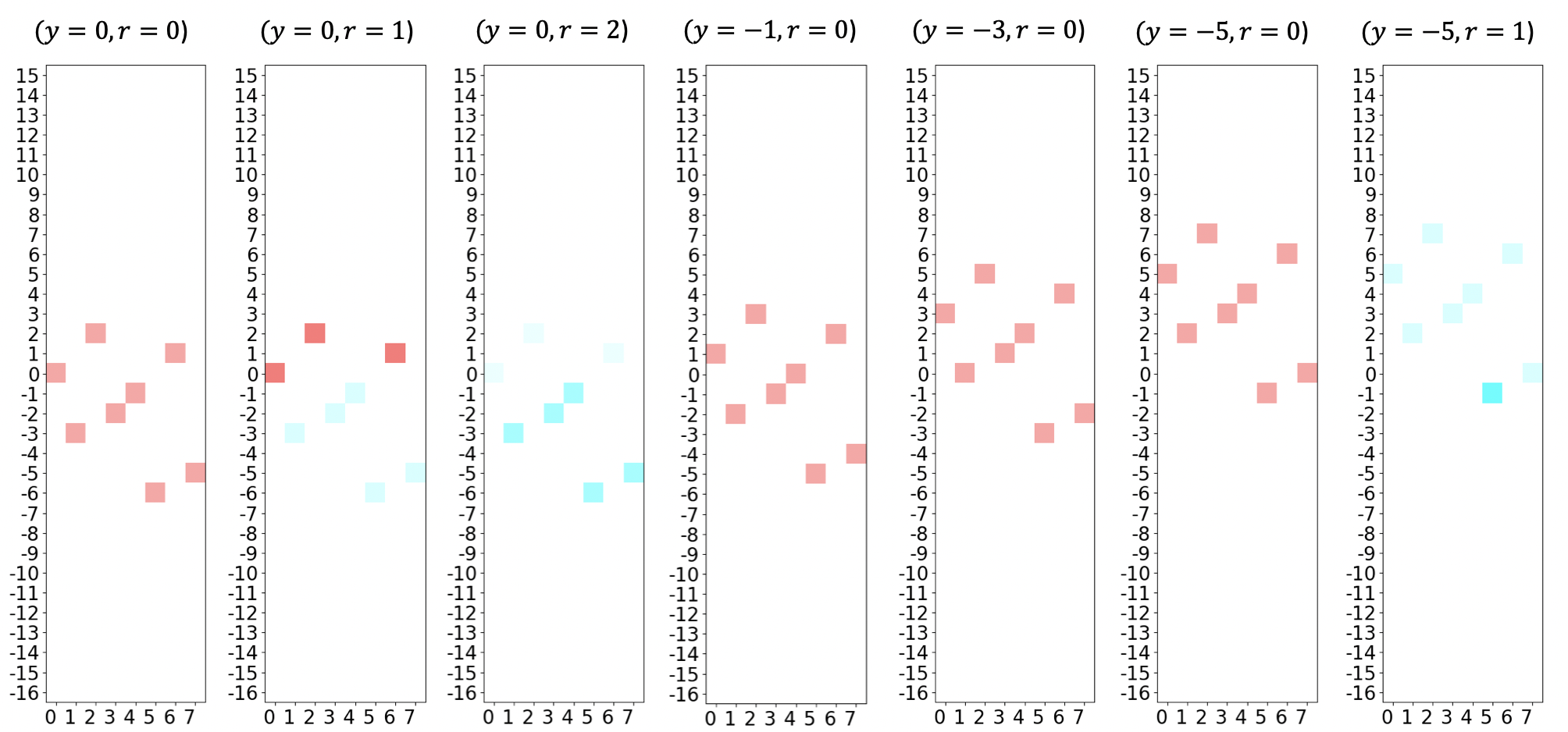
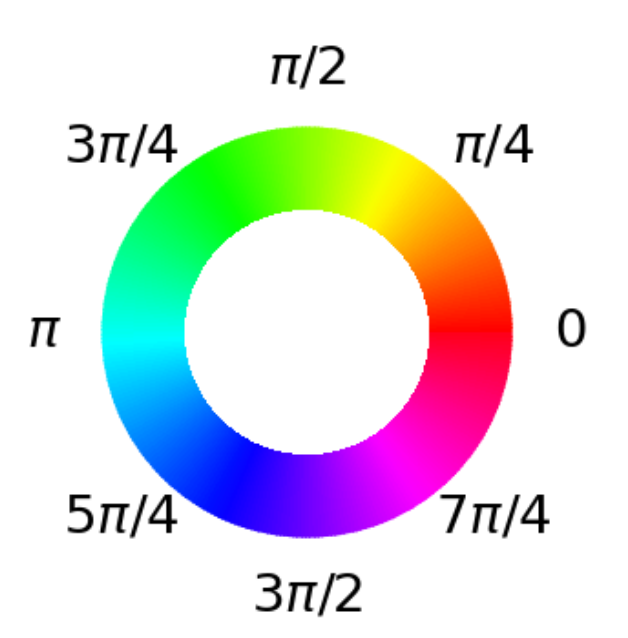
Cada gráfica muestra una sola iteración de GAS, con los valores actuales de \(r\) (= contador de iteraciones) y \(y\) (= umbral/compensación) mostrados en el título. El eje X muestra el entero equivalente de la entrada (ppor ejemplo, “101” \(\rightarrow\) 5), y el eje Y muestra los posibles valores de la función. Como hay 3 variables binarias, hay \(2^3=8\) posibles soluciones, que se muestran en cada gráfica. La intensidad del color indica la probabilidad de medir un resultado determinado (siendo la intensidad del brillo la más alta), mientras que el color en sí indica la fase correspondiente (consulta la rueda de color de fase a continuación). Ten en cuenta que a medida que \(y\) disminuye, desplazamos todos los valores hacia arriba por esa cantidad, lo que significa que hay cada vez menos valores negativos en la distribución, hasta que solo queda uno (el mínimo).

Comprobar que GroverOptimizer encuentra el valor correcto

Podemos verificar que el algoritmo está funcionando correctamente usando el MinimumEigenOptimizer en Qiskit Optimization.

exact_solver = MinimumEigenOptimizer(NumPyMinimumEigensolver())
exact_result = exact_solver.solve(qp)
print(exact_result.prettyprint())

objective function value: -6.0
variable values: x0=1.0, x1=0.0, x2=1.0
status: SUCCESS

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
qiskit-terra	0.23.0
qiskit-aer	0.11.1
qiskit-optimization	0.5.0
qiskit-machine-learning	0.6.0
System information
Python version	3.9.15
Python compiler	Clang 14.0.0 (clang-1400.0.29.102)
Python build	main, Oct 11 2022 22:27:25
OS	Darwin
CPUs	4
Memory (Gb)	16.0
Tue Dec 06 21:47:01 2022 JST

This code is a part of Qiskit

© Copyright IBM 2017, 2022.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.