নোট

এই পৃষ্ঠাটি docs/tutorials/04_grover_optimizer.ipynb থেকে বানানো হয়েছে।

গ্রোভার অপ্টিমাইজার

ভূমিকা

গ্রোভার এডাপটিভ সার্চ (GAS) কে সংমিশ্রণমূলক অপ্টিমাইজেশন সমস্যার পাশাপাশি পরিবর্তনশীল (ভ্যারিয়েশনাল) অ্যালগরিদম, যেমন Variational Quantum Eigensolver (VQE) এবং Quantum Approximate Optimization Algorithm (QAOA) এর সম্ভাব্য সমাধান হিসাবে অন্বেষণ করা হয়েছে। এই অ্যালগরিদমটি একটি অব্জেক্টিভ ফাংশন এর সর্বোত্তম মানটি সন্ধান করার জন্য পুনরুক্তি ভাবে গ্রোভার অনুসন্ধান প্রয়োগ করে, যেটা প্রান্তিক হিসাবে আগের রান থেকে সর্বাধিক পরিচিত মান ব্যবহার করে। GAS-এ ব্যবহৃত অভিযোজিত ওরাকল বর্তমান প্রান্তিকের উপরে বা নীচে (যথাক্রমে সর্বাধিক এবং সর্বনিম্ন জন্য) সমস্ত মানকে স্বীকৃতি দেয়, যতক্ষণ না কোনও সর্বোত্তম সন্ধান পাওয়া যায় ততক্ষণ প্রতিটি পুনরাবৃত্তির প্রান্তিক আপডেট হয় সন্ধানের জায়গার আকার হ্রাস করে।

[1] এ বর্ণিত শর্তহীন দ্বিঘাত দ্বিমিক অনুকূলায়ন (অপ্টিমাইজেশন) সমস্যাটিকে হ্রাস করার মাধ্যমে এই নোটবুকে আমরা GroverOptimizer এর প্রত্যেকটি উপাদান সম্পর্কে জানব যেগুলো জি এ এস-এ বর্ণিত উপায়গুলোকে ব্যবহার করে।

তথ্যসূত্র

[1] A. Gilliam, S. Woerner, C. Gonciulea, Grover Adaptive Search for Constrained Polynomial Binary Optimization, arXiv preprint arXiv:1912.04088 (2019).

গ্রোভার অ্যাডাপটিভ সার্চ

GAS এর মূল উপাদান গ্রোভার সার্চের জন্য তিনটি উপাদান প্রয়োজন:

1. একটি মান প্রস্তুতি অপারেটর \(A\) সার্চ স্পেসে সমস্ত মানের জন্য একটি উপরিপাতন তৈরি করে।

2. একটি ওরাকল অপারেটর \(O\) যা আগ্রহের মানগুলি স্বীকৃতি দেয় এবং তাদের বিস্তার -1 দ্বারা বহুগুণ করে।

3. Grover ব্যাপ্তি অপারেটর \(D\), যা \(|0\rangle_n\) বিস্তার এর মান কে -১ দ্বারা গুন করে।

GAS বাস্তবায়ন নির্দিষ্ট ব্যবহারের ক্ষেত্রে প্রায় পৃথক হলেও সাধারণ কাঠামো এখনও নীচে বর্ণিত পদক্ষেপগুলি আলগাভাবে অনুসরণ করে।

GroverOptimizer \(A_y`নির্মাণ করতে ``QuadraticProgramToNegativeValueOracle`\) ব্যবহার করে যাতে এটা :math::n-qubit রেজিস্টার প্রস্তুত করে যাতে উপরিপাতন প্রতিনিধিত্ব করতে সব \(|x\rangle_n\) এবং একটি \(m\)-qubit রেজিস্টার (আনুমানিক) \(|Q(x)-y\rangle_m\) উপস্থাপন করুন।তারপরে, \((Q(x) - y)\) নেতিবাচক সমস্ত মানগুলি \(O_y\) পতাকা দ্বারা চিহ্নিত করা উচিত। নোট করুন, যে আলোচিত বাস্তবায়নে, ওরাকল অপারেটরটি আসলে \(y\) এর থেকে স্বতন্ত্র, তবে এটি কোনো প্রয়োজন নয়। স্পষ্টতার জন্য, যখন ওরাকলটি \(y\) থেকে স্বতন্ত্র থাকে, তখন আমরা ওরাকলকে \(O\) হিসাবে উল্লেখ করব।

রীত্যনুসারে QuadraticProgramToNegativeValueOracle \(A_y\) এবং \(O\) গঠন করে যাতে:

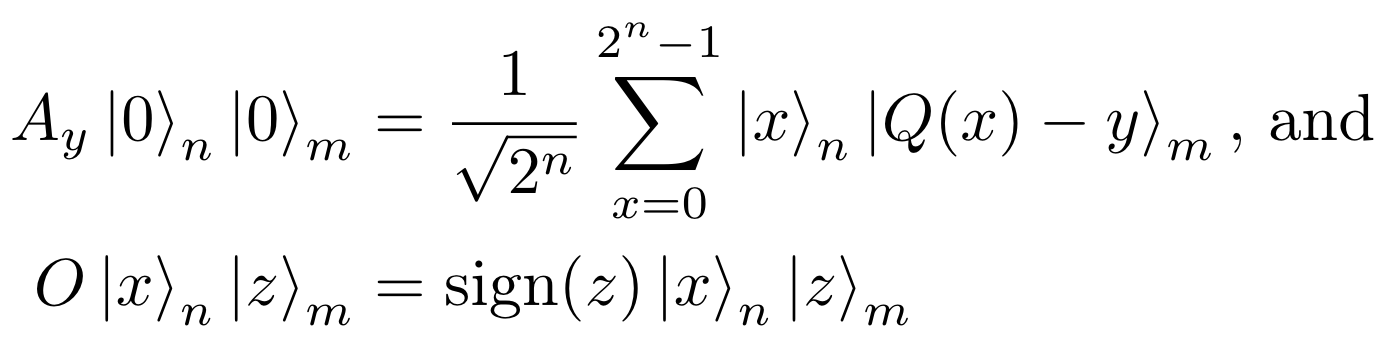
যেখানে \(|x\rangle\) হল \(x\) অখণ্ড সংখ্যার দ্বিমিক (বাইনারি) এনকোডিং।

প্রতিটি পুনরাবৃত্তিতে যেখানে প্রান্তিক \(y\) আপডেট করা হয়, আমরা অভিযোজিত :math:` A_y` যেমন ফাংশন মানগুলি উপরে বা নিচে স্থানান্তরিত হয় (যথাক্রমে সর্বনিম্ন এবং সর্বাধিকের জন্য) দ্বারা \(y\)। উদাহরণস্বরূপ, সর্বনিম্ন সন্ধানের প্রসঙ্গে, যেমন \(y\) এর মান হ্রাস হয়, অনুসন্ধানের স্থানো (নেতিবাচক মান) হ্রাস পায়, যতক্ষণ না কেবল সর্বনিম্ন মান থাকে। এর একটি অবয়ববিশিষ্ট উদাহরণ পরবর্তী বিভাগে খুঁজা হবে।

GroverOptimizer ব্যবহার করে কোনো ন্যূনতম QUBO সমস্যার সন্ধান করুন

নিম্নলিখিত একটি লঘুকরণ সমস্যার একটি ছোট্ট উদাহরণ আছে।

\begin{eqnarray} \min_{x \in \{0, 1\}^3} -2x_0x_2 - x_1x_2 - 1x_0 + 2x_1 - 3x_2. \end{eqnarray}

প্রাথমিক পদক্ষেপরূপে আমরা একটি ডকপ্লেক্স মডেল তৈরি করব যেটা উপরের সমস্যাটিকে সংজ্ঞায়িত করবে, তারপর মডেলটিকে একটি QuadraticProgram এ রূপান্তর করতে from_docplex() ফাংশনটি ব্যবহার করব, যা Qiskit অনুকূলকরণে (অপ্টিমাইজেশন) একটা QUBO এর প্রতিনিধিত্ব করতে পারে।

from qiskit_algorithms import NumPyMinimumEigensolver
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import GroverOptimizer, MinimumEigenOptimizer
from qiskit_optimization.translators import from_docplex_mp
from docplex.mp.model import Model

model = Model()
x0 = model.binary_var(name="x0")
x1 = model.binary_var(name="x1")
x2 = model.binary_var(name="x2")
model.minimize(-x0 + 2 * x1 - 3 * x2 - 2 * x0 * x2 - 1 * x1 * x2)
qp = from_docplex_mp(model)
print(qp.prettyprint())

Problem name: docplex_model1

Minimize
  -2*x0*x2 - x1*x2 - x0 + 2*x1 - 3*x2

Subject to
  No constraints

  Binary variables (3)
    x0 x1 x2

Next, we create a GroverOptimizer that uses 6 qubits to encode the value, and will terminate after there have been 10 iterations of GAS without progress (i.e. the value of \(y\) does not change). The solve() function takes the QuadraticProgram we created earlier, and returns a results object that contains information about the run.

grover_optimizer = GroverOptimizer(6, num_iterations=10, sampler=Sampler())
results = grover_optimizer.solve(qp)
print(results.prettyprint())

objective function value: -6.0
variable values: x0=1.0, x1=0.0, x2=1.0
status: SUCCESS

এটি সর্বোত্তম সমাধানে ফলাফল \(x_0 = 1\), :math:` x_1 = 0`, :math: x_2 = 1 এবং সর্বোত্তম উদ্দেশ্য মান :math:` -6` (বেশিরভাগ সময়, যেহেতু এটি রন্ডমাইজড অ্যালগরিদম)। নিম্নলিখিতটিতে, কোয়ান্টাম মানের একটি বিশেষায়িত চিত্রায়ন (কাস্টম ভিজ্যুয়ালাইজেশন) এই QUBO তে প্রয়োগ হওয়া GroverOptimizer এর একটি সম্ভাব্য রান দেখায়।

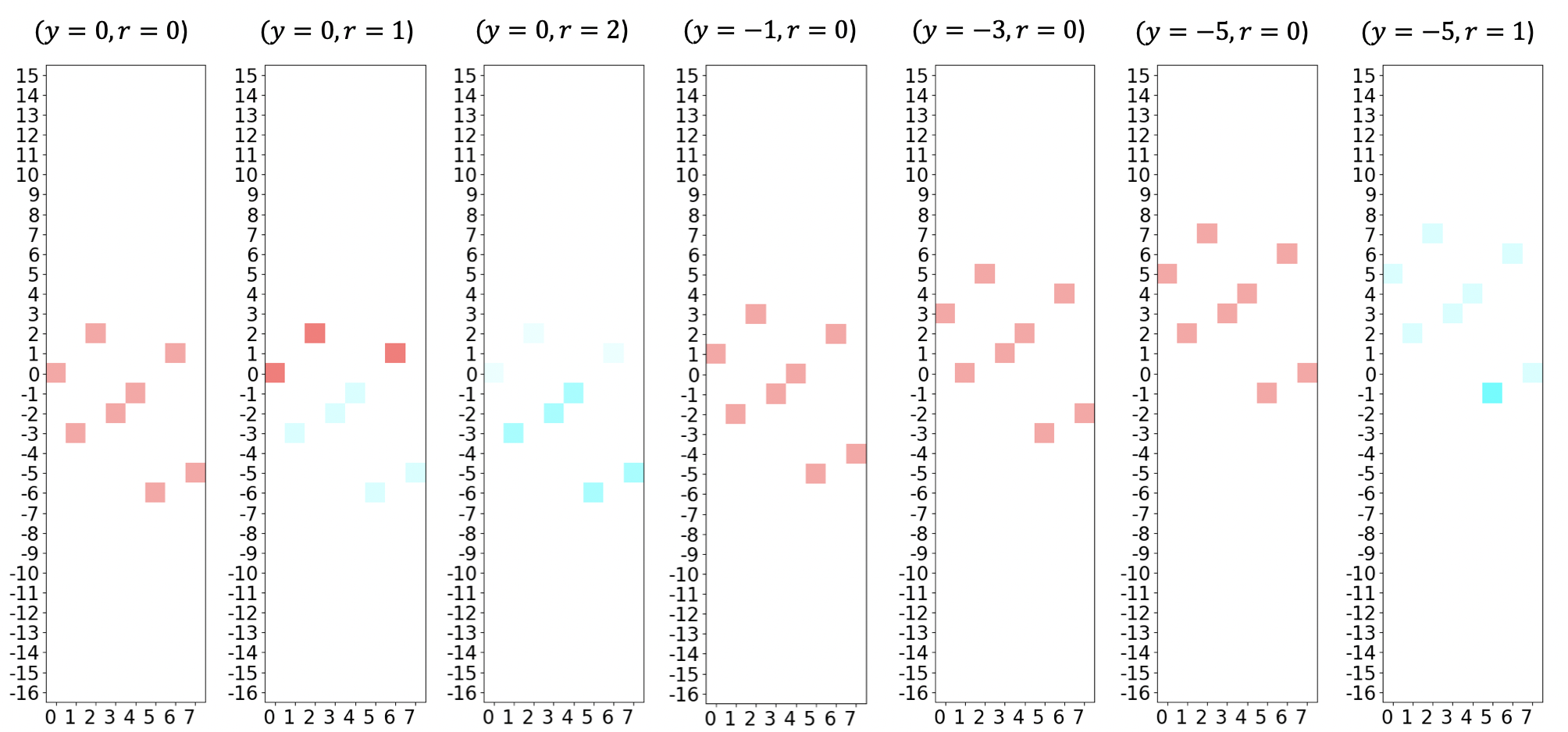
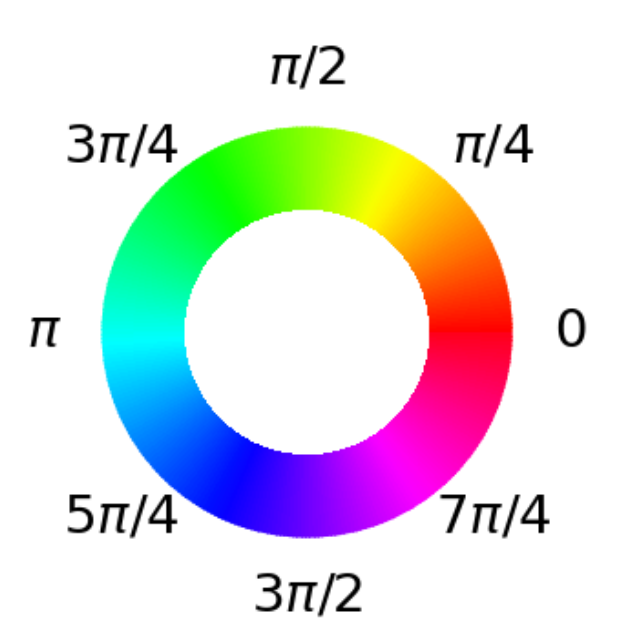
Each graph shows a single iteration of GAS, with the current values of \(r\) (= iteration counter) and \(y\) (= threshold/offset) shown in the title. The X-axis displays the integer equivalent of the input (e.g. '101' \(\rightarrow\) 5), and the Y-axis shows the possible function values. As there are 3 binary variables, there are \(2^3=8\) possible solutions, which are shown in each graph. The color intensity indicates the probability of measuring a certain result (with bright intensity being the highest), while the actual color indicates the corresponding phase (see phase color-wheel below). Note that as \(y\) decreases, we shift all of the values up by that amount, meaning there are fewer and fewer negative values in the distribution, until only one remains (the minimum).

পরীক্ষা করে দেখুন যে GroverOptimizer সঠিক মানটি পাচ্ছে

We can verify that the algorithm is working correctly using the MinimumEigenOptimizer in Qiskit optimization.

exact_solver = MinimumEigenOptimizer(NumPyMinimumEigensolver())
exact_result = exact_solver.solve(qp)
print(exact_result.prettyprint())

objective function value: -6.0
variable values: x0=1.0, x1=0.0, x2=1.0
status: SUCCESS

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
qiskit-terra	0.23.0
qiskit-aer	0.11.1
qiskit-optimization	0.5.0
qiskit-machine-learning	0.6.0
System information
Python version	3.9.15
Python compiler	Clang 14.0.0 (clang-1400.0.29.102)
Python build	main, Oct 11 2022 22:27:25
OS	Darwin
CPUs	4
Memory (Gb)	16.0
Tue Dec 06 21:47:01 2022 JST

This code is a part of Qiskit

© Copyright IBM 2017, 2022.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.