নোট

এই পেজটি docs/tutorials/09_application_classes.ipynb থেকে তৈরি হয়েছে।

অপ্টিমাইজেশন সমস্যার জন্য অ্যাপ্লিকেশন ক্লাস#

ভূমিকা#

আমরা নিম্নলিখিত অপ্টিমাইজেশান সমস্যার জন্য অ্যাপ্লিকেশন ক্লাস চালু করি যাতে ব্যবহারকারীরা সহজেই কোয়ান্টাম কম্পিউটারে বিভিন্ন অপ্টিমাইজেশান সমস্যার চেষ্টা করতে পারে।

Exact কভার সমস্যা

আইটেমের উপসেটগুলির একটি সংগ্রহ দেওয়া, একটি উপ -সংগ্রহ খুঁজুন যাতে প্রতিটি আইটেম ঠিক একবার আচ্ছাদিত হয়।

ন্যাপস্যাক সমস্যা

আইটেমের একটি সেট দেওয়া, আইটেমগুলির একটি উপসেট খুঁজুন যাতে মোট ওজন ধারণক্ষমতার মধ্যে থাকে এবং মোট মান সর্বাধিক হয়।

সংখ্যা বিভাজন সমস্যা

ধনাত্মক পূর্ণসংখ্যার একটি মাল্টিসেট দেওয়া হলে, মাল্টিসেটের একটি বিভাজন দুটি উপসেটগুলিতে খুঁজুন যাতে উপসেটগুলির যোগফল সমান হয়।

সেট প্যাকিং সমস্যা

আইটেমের উপসেটগুলির একটি সংগ্রহ দেওয়া হলে, এমন একটি উপ -সংগ্রহ খুঁজুন যাতে উপ -সংগ্রহের সমস্ত উপগোষ্ঠী জোড়া যুক্ত হয় এবং উপ -সংগ্রহে আইটেমের সংখ্যা সর্বাধিক হয়।

গ্রাফ সমস্যা

ক্লিকে সমস্যা

একটি অনির্দেশিত গ্রাফ দেওয়া, একটি নির্দিষ্ট সংখ্যা বা সর্বাধিক সংখ্যক নোডগুলির একটি উপসেট খুঁজুন যাতে প্ররোচিত সাবগ্রাফটি সম্পূর্ণ হয়।

গ্রাফ পার্টিশন সমস্যা

একটি অনির্দেশিত গ্রাফ দেওয়া, দুটি অংশে একটি পার্টিশন খুঁজুন যার আকার সমান যে দুটি উপাদানগুলির মধ্যে প্রান্তের মোট ক্ষমতা কমিয়ে আনা হয়।

সর্বোচ্চ-কাট সমস্যা (Max-Cut problem)

একটি অনির্দেশিত গ্রাফ দেওয়া, দুটি উপসেটগুলিতে নোডের একটি পার্টিশন খুঁজুন যাতে দুটি উপসেটগুলির মধ্যে প্রান্তের মোট ওজন সর্বাধিক হয়।

স্থিত সেট সমস্যা

একটি অনির্দেশিত গ্রাফ দেওয়া, নোডের একটি উপসেট খুঁজুন যাতে কোন প্রান্ত উপসেটগুলির নোডগুলিকে সংযুক্ত না করে এবং নোডের সংখ্যা সর্বাধিক হয়।

ট্রাভেলিং সেলসম্যান সমস্যা

একটি গ্রাফ দেওয়া, ন্যূনতম দূরত্ব সহ একটি রুট খুঁজুন যাতে রুটটি প্রতিটি শহরে একবার ঠিক ভিজিট করে।

যানবাহন চলাচলের সমস্যা

একটি গ্রাফ, একটি ডিপো নোড এবং যানবাহনের সংখ্যা (রুট) দেওয়া হলে, রুটগুলির একটি সেট খুঁজুন যাতে প্রতিটি নোড ডিপো ছাড়া ঠিক একবার আচ্ছাদিত হয় এবং রুটগুলির মোট দূরত্ব কম হয়।

ভারটেক্স কভার সমস্যা

একটি অনির্দেশিত গ্রাফ দেওয়া, ন্যূনতম আকারের নোডগুলির একটি উপসেট খুঁজুন যাতে প্রতিটি প্রান্তের উপসেটগুলিতে কমপক্ষে একটি শেষ বিন্দু থাকে।

গ্রাফ সমস্যার জন্য অ্যাপ্লিকেশন ক্লাস (GraphOptimizationApplication) একটি দৃষ্টান্ত এবং ফলাফলের গ্রাফ আঁকার জন্য একটি কার্যকারিতা প্রদান করে। নোট করুন যে কার্যকারিতাটি ব্যবহার করার জন্য আপনাকে আগে থেকেই matplotlib ইনস্টল করতে হবে।

আমরা এই পৃষ্ঠায় ভারটেক্স কভার সমস্যা এবং ন্যাপস্যাক সমস্যার উদাহরণ উপস্থাপন করি।

ম্যাক্স-কাট সমস্যা এবং ট্রাভেলিং সেলসম্যান সমস্যার উদাহরণ Max-Cut and Traveling Salesman Problem তে পাওয়া যায়।

আমরা প্রথমে অ্যাপ্লিকেশন ক্লাসের জন্য প্রয়োজনীয় প্যাকেজ আমদানি করি।

[1]:

from qiskit_optimization.algorithms import MinimumEigenOptimizer
from qiskit_algorithms.utils import algorithm_globals
from qiskit_algorithms import QAOA, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import COBYLA
from qiskit.primitives import Sampler

ভারটেক্স কভার সমস্যা#

আমরা গ্রাফ সমস্যার উদাহরণ হিসাবে শিরোনাম কভার সমস্যার জন্য অ্যাপ্লিকেশন ক্লাস চালু করি। একটি অনির্দেশিত গ্রাফ দেওয়া, শিরোনাম কভার সমস্যাটি আমাদেরকে ন্যূনতম আকারের নোডগুলির একটি উপসেট খুঁজে পেতে বলে, যাতে সমস্ত প্রান্তগুলি নির্বাচিত কোনও নোড দ্বারা আবৃত থাকে।

আমরা ভারটেক্স কভার সমস্যা এবং networkx দৈব গ্রাফ তৈরির জন্য অ্যাপ্লিকেশন শ্রেণী VertexCover আমদানি করি।

[2]:

from qiskit_optimization.applications.vertex_cover import VertexCover
import networkx as nx

seed = 123
algorithm_globals.random_seed = seed

[3]:

graph = nx.random_regular_graph(d=3, n=6, seed=seed)
pos = nx.spring_layout(graph, seed=seed)

[4]:

prob = VertexCover(graph)
prob.draw(pos=pos)

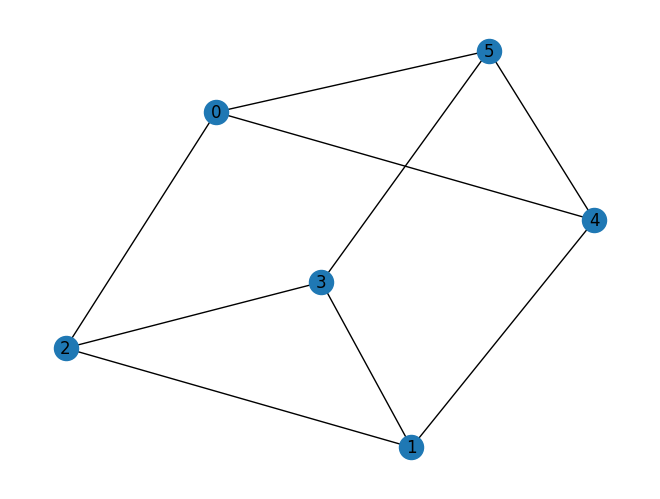
../_images/tutorials_09_application_classes_8_0.png

VertexCover একটি গ্রাফ গ্রহন করে একটি উদাহরণ হিসেবে এবং to_quadratic_program তৈরি করে একটি অনুরূপ QuadraticProgram যা ভারটেক্স কভার সমস্যার উদাহরণ তৈরি করে।

[5]:

qp = prob.to_quadratic_program()
print(qp.prettyprint())

Problem name: Vertex cover

Minimize
  x_0 + x_1 + x_2 + x_3 + x_4 + x_5

Subject to
  Linear constraints (9)
    x_1 + x_2 >= 1  'c0'
    x_1 + x_4 >= 1  'c1'
    x_1 + x_3 >= 1  'c2'
    x_2 + x_3 >= 1  'c3'
    x_0 + x_2 >= 1  'c4'
    x_0 + x_4 >= 1  'c5'
    x_0 + x_5 >= 1  'c6'
    x_4 + x_5 >= 1  'c7'
    x_3 + x_5 >= 1  'c8'

  Binary variables (6)
    x_0 x_1 x_2 x_3 x_4 x_5

আপনি নিম্নরূপ সমস্যা সমাধান করতে পারেন। NumPyMinimumEigensolver সর্বনিম্ন eigen ভেক্টর খুঁজে পায়। আপনি QAOA প্রয়োগ করতে পারেন। মনে রাখবেন QAOA দ্বারা সমাধান সবসময় অনুকূল নয়।

[6]:

# Numpy Eigensolver
meo = MinimumEigenOptimizer(min_eigen_solver=NumPyMinimumEigensolver())
result = meo.solve(qp)
print(result.prettyprint())
print("\nsolution:", prob.interpret(result))
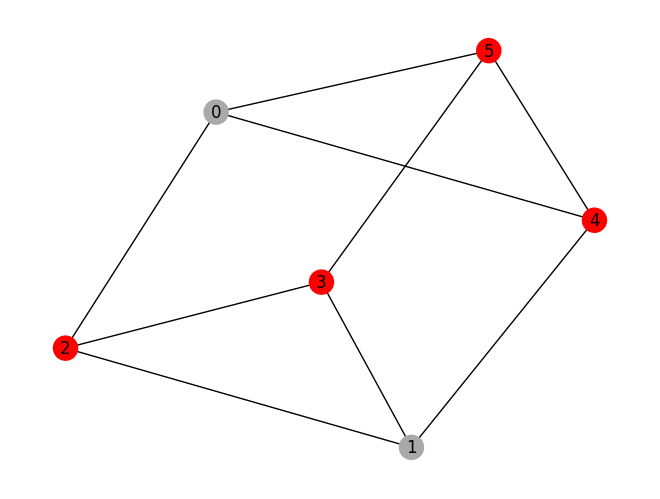
prob.draw(result, pos=pos)

objective function value: 4.0
variable values: x_0=0.0, x_1=0.0, x_2=1.0, x_3=1.0, x_4=1.0, x_5=1.0
status: SUCCESS

solution: [2, 3, 4, 5]

../_images/tutorials_09_application_classes_12_1.png

[7]:

# QAOA
meo = MinimumEigenOptimizer(min_eigen_solver=QAOA(reps=1, sampler=Sampler(), optimizer=COBYLA()))
result = meo.solve(qp)
print(result.prettyprint())
print("\nsolution:", prob.interpret(result))
print("\ntime:", result.min_eigen_solver_result.optimizer_time)
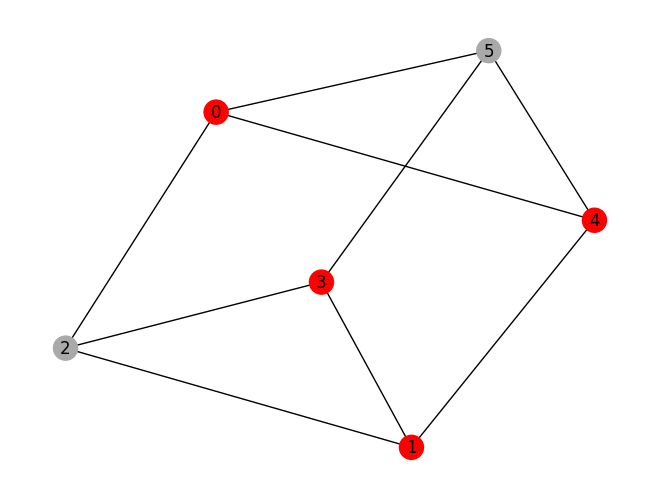
prob.draw(result, pos=pos)

objective function value: 4.0
variable values: x_0=1.0, x_1=1.0, x_2=0.0, x_3=1.0, x_4=1.0, x_5=0.0
status: SUCCESS

solution: [0, 1, 3, 4]

time: 2.721126079559326

../_images/tutorials_09_application_classes_13_1.png

ন্যাপস্যাক সমস্যা#

ন্যাপস্যাক সমস্যাটি আমাদের আইটেমের সংমিশ্রণ খুঁজে পেতে বলে, যাতে মোট ওজন ন্যাপস্যাকের ধারণক্ষমতার মধ্যে থাকে এবং আইটেমের মোট মূল্য সর্বাধিক হয়। নিচের উদাহরণগুলি NumPy eigensolver এবং কিউএওএ দ্বারা 5 টি আইটেমের সাথে ন্যাপস্যাক সমস্যার একটি উদাহরণ সমাধান করে।

[8]:

from qiskit_optimization.applications import Knapsack

[9]:

prob = Knapsack(values=[3, 4, 5, 6, 7], weights=[2, 3, 4, 5, 6], max_weight=10)
qp = prob.to_quadratic_program()
print(qp.prettyprint())

Problem name: Knapsack

Maximize
  3*x_0 + 4*x_1 + 5*x_2 + 6*x_3 + 7*x_4

Subject to
  Linear constraints (1)
    2*x_0 + 3*x_1 + 4*x_2 + 5*x_3 + 6*x_4 <= 10  'c0'

  Binary variables (5)
    x_0 x_1 x_2 x_3 x_4

[10]:

# Numpy Eigensolver
meo = MinimumEigenOptimizer(min_eigen_solver=NumPyMinimumEigensolver())
result = meo.solve(qp)
print(result.prettyprint())
print("\nsolution:", prob.interpret(result))

objective function value: 13.0
variable values: x_0=1.0, x_1=1.0, x_2=0.0, x_3=1.0, x_4=0.0
status: SUCCESS

solution: [0, 1, 3]

[11]:

# QAOA
meo = MinimumEigenOptimizer(min_eigen_solver=QAOA(reps=1, sampler=Sampler(), optimizer=COBYLA()))
result = meo.solve(qp)
print(result.prettyprint())
print("\nsolution:", prob.interpret(result))
print("\ntime:", result.min_eigen_solver_result.optimizer_time)

objective function value: 13.0
variable values: x_0=1.0, x_1=1.0, x_2=0.0, x_3=1.0, x_4=0.0
status: SUCCESS

solution: [0, 1, 3]

time: 2.0846190452575684

কিভাবে হ্যামিল্টোনিয়ান চেক করবেন#

আপনি যদি আপনার সমস্যার উদাহরণ থেকে উৎপন্ন প্রকৃত হ্যামিল্টোনিয়ান পরীক্ষা করতে চান, তাহলে আপনাকে নিম্নরূপ একটি রূপান্তরকারী প্রয়োগ করতে হবে।

[12]:

from qiskit_optimization.converters import QuadraticProgramToQubo

[13]:

# the same knapsack problem instance as in the previous section
prob = Knapsack(values=[3, 4, 5, 6, 7], weights=[2, 3, 4, 5, 6], max_weight=10)
qp = prob.to_quadratic_program()
print(qp.prettyprint())

Problem name: Knapsack

Maximize
  3*x_0 + 4*x_1 + 5*x_2 + 6*x_3 + 7*x_4

Subject to
  Linear constraints (1)
    2*x_0 + 3*x_1 + 4*x_2 + 5*x_3 + 6*x_4 <= 10  'c0'

  Binary variables (5)
    x_0 x_1 x_2 x_3 x_4

[14]:

# intermediate QUBO form of the optimization problem
conv = QuadraticProgramToQubo()
qubo = conv.convert(qp)
print(qubo.prettyprint())

Problem name: Knapsack

Minimize
  26*c0@int_slack@0^2 + 104*c0@int_slack@0*c0@int_slack@1
  + 208*c0@int_slack@0*c0@int_slack@2 + 156*c0@int_slack@0*c0@int_slack@3
  + 104*c0@int_slack@1^2 + 416*c0@int_slack@1*c0@int_slack@2
  + 312*c0@int_slack@1*c0@int_slack@3 + 416*c0@int_slack@2^2
  + 624*c0@int_slack@2*c0@int_slack@3 + 234*c0@int_slack@3^2
  + 104*x_0*c0@int_slack@0 + 208*x_0*c0@int_slack@1 + 416*x_0*c0@int_slack@2
  + 312*x_0*c0@int_slack@3 + 104*x_0^2 + 312*x_0*x_1 + 416*x_0*x_2 + 520*x_0*x_3
  + 624*x_0*x_4 + 156*x_1*c0@int_slack@0 + 312*x_1*c0@int_slack@1
  + 624*x_1*c0@int_slack@2 + 468*x_1*c0@int_slack@3 + 234*x_1^2 + 624*x_1*x_2
  + 780*x_1*x_3 + 936*x_1*x_4 + 208*x_2*c0@int_slack@0 + 416*x_2*c0@int_slack@1
  + 832*x_2*c0@int_slack@2 + 624*x_2*c0@int_slack@3 + 416*x_2^2 + 1040*x_2*x_3
  + 1248*x_2*x_4 + 260*x_3*c0@int_slack@0 + 520*x_3*c0@int_slack@1
  + 1040*x_3*c0@int_slack@2 + 780*x_3*c0@int_slack@3 + 650*x_3^2 + 1560*x_3*x_4
  + 312*x_4*c0@int_slack@0 + 624*x_4*c0@int_slack@1 + 1248*x_4*c0@int_slack@2
  + 936*x_4*c0@int_slack@3 + 936*x_4^2 - 520*c0@int_slack@0
  - 1040*c0@int_slack@1 - 2080*c0@int_slack@2 - 1560*c0@int_slack@3 - 1043*x_0
  - 1564*x_1 - 2085*x_2 - 2606*x_3 - 3127*x_4 + 2600

Subject to
  No constraints

  Binary variables (9)
    x_0 x_1 x_2 x_3 x_4 c0@int_slack@0 c0@int_slack@1 c0@int_slack@2
    c0@int_slack@3

[15]:

# qubit Hamiltonian and offset
op, offset = qubo.to_ising()
print(f"num qubits: {op.num_qubits}, offset: {offset}\n")
print(op)

num qubits: 9, offset: 1417.5

SparsePauliOp(['IIIIIIIIZ', 'IIIIIIIZI', 'IIIIIIZII', 'IIIIIZIII', 'IIIIZIIII', 'IIIZIIIII', 'IIZIIIIII', 'IZIIIIIII', 'ZIIIIIIII', 'IIIIIIIZZ', 'IIIIIIZIZ', 'IIIIIIZZI', 'IIIIIZIIZ', 'IIIIIZIZI', 'IIIIIZZII', 'IIIIZIIIZ', 'IIIIZIIZI', 'IIIIZIZII', 'IIIIZZIII', 'IIIZIIIIZ', 'IIIZIIIZI', 'IIIZIIZII', 'IIIZIZIII', 'IIIZZIIII', 'IIZIIIIIZ', 'IIZIIIIZI', 'IIZIIIZII', 'IIZIIZIII', 'IIZIZIIII', 'IIZZIIIII', 'IZIIIIIIZ', 'IZIIIIIZI', 'IZIIIIZII', 'IZIIIZIII', 'IZIIZIIII', 'IZIZIIIII', 'IZZIIIIII', 'ZIIIIIIIZ', 'ZIIIIIIZI', 'ZIIIIIZII', 'ZIIIIZIII', 'ZIIIZIIII', 'ZIIZIIIII', 'ZIZIIIIII', 'ZZIIIIIII'],
              coeffs=[-258.5+0.j, -388. +0.j, -517.5+0.j, -647. +0.j, -776.5+0.j, -130. +0.j,
 -260. +0.j, -520. +0.j, -390. +0.j,   78. +0.j,  104. +0.j,  156. +0.j,
  130. +0.j,  195. +0.j,  260. +0.j,  156. +0.j,  234. +0.j,  312. +0.j,
  390. +0.j,   26. +0.j,   39. +0.j,   52. +0.j,   65. +0.j,   78. +0.j,
   52. +0.j,   78. +0.j,  104. +0.j,  130. +0.j,  156. +0.j,   26. +0.j,
  104. +0.j,  156. +0.j,  208. +0.j,  260. +0.j,  312. +0.j,   52. +0.j,
  104. +0.j,   78. +0.j,  117. +0.j,  156. +0.j,  195. +0.j,  234. +0.j,
   39. +0.j,   78. +0.j,  156. +0.j])

[16]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
`qiskit-terra`	0.25.0.dev0+1d844ec
`qiskit-aer`	0.12.0
`qiskit-ibmq-provider`	0.20.2
`qiskit-nature`	0.7.0
`qiskit-optimization`	0.6.0
System information
Python version	3.10.11
Python compiler	Clang 14.0.0 (clang-1400.0.29.202)
Python build	main, Apr 7 2023 07:31:31
OS	Darwin
CPUs	4
Memory (Gb)	16.0
Thu May 18 16:57:10 2023 JST

This code is a part of Qiskit

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.

[ ]: