নোট

এই পৃষ্ঠাটি docs/tutorials/06_examples_max_cut_and_tsp.ipynb থেকে বানানো হয়েছে।

সর্বোচ্চ লাভ এবং ট্রাভেলিং সেলসম্যান সমস্যা

ভূমিকা

পরিমাণ ক্ষেত্রের অনেকগুলি সমস্যা যেমন ব্যবস্থাপনাবিদ্যা এবং ইঞ্জিনিয়ারিং হল অনুকূলায়ন (অপ্টিমাইজেশন) সমস্যাসমূহ। অনুকূলায়ন (অপ্টিমাইজেশন) সমস্যাগুলি জটিল সিদ্ধান্ত গ্রহণ এবং কৌশলগুলির সংজ্ঞার মূল ভিত্তিতে থাকে।

অপ্টিমাইজেশন (বা সমাবেশীয় অনুকূলায়ন (অপ্টিমাইজেশন)) এর অর্থ সীমাবদ্ধ বা সম্ভাব্য সমাধানের অসীম সেটগুলিতে একটি অনুকূল সমাধান অনুসন্ধান করা। অনুকূলতাটি কিছু মানদণ্ডের ফাংশনের প্রতি সম্মানের সাথে সংজ্ঞায়িত করা হয়, যা ছোট বা সর্বাধিক করতে হবে। একে সাধারণত কস্ট ফাংশন বা নৈর্ব্যক্তিক অন্বয় (অব্জেক্টিভ ফাংশন) বলা হয়।

সাধারণ অনুকূলায়ন (অপ্টিমাইজেশন) সমস্যাসমূহ

হ্রাসকরণ: ব্যয়, দূরত্ব, একটি ট্র্যাভারসাল দৈর্ঘ্য, ওজন, প্রক্রিয়াকরণের সময়, উপাদান, শক্তি খরচ, বস্তুর (অবজেক্ট) সংখ্যা

সর্বাধিকীকরণ: লাভ, মান, আউটপুট, রিটার্ন, ফলন, উপযোগ, দক্ষতা, ক্ষমতা, বস্তুর (অবজেক্ট) সংখ্যা

We consider here max-cut problems of practical interest in many fields, and show how they can be mapped on quantum computers manually and how Qiskit optimization module supports this.

Weighted Max-Cut

Max-Cut is an NP-complete problem, with applications in clustering, network science, and statistical physics. To grasp how practical applications are mapped into given Max-Cut instances, consider a system of many people that can interact and influence each other. Individuals can be represented by vertices of a graph, and their interactions seen as pairwise connections between vertices of the graph, or edges. With this representation in mind, it is easy to model typical marketing problems. For example, suppose that it is assumed that individuals will influence each other’s buying decisions, and knowledge is given about how strong they will influence each other. The influence can be modeled by weights assigned on each edge of the graph. It is possible then to predict the outcome of a marketing strategy in which products are offered for free to some individuals, and then ask which is the optimal subset of individuals that should get the free products, in order to maximize revenues.

এই সমস্যার আনুষ্ঠানিক সংজ্ঞাটি হল:

Consider an \(n\)-node undirected graph G = (V, E) where |V| = n with edge weights \(w_{ij}>0\), \(w_{ij}=w_{ji}\), for \((i, j)\in E\). A cut is defined as a partition of the original set V into two subsets. The cost function to be optimized is in this case the sum of weights of edges connecting points in the two different subsets, crossing the cut. By assigning \(x_i=0\) or \(x_i=1\) to each node \(i\), one tries to maximize the global profit function (here and in the following summations run over indices 0,1,…n-1)

\[\tilde{C}(\textbf{x}) = \sum_{i,j} w_{ij} x_i (1-x_j) ।\]

আমাদের সাধারণ বিপণন মডেলটিতে, \(w_{ij}\) এই সম্ভাব্যতা উপস্থাপন করে যে \(j\) ব্যক্তি \(i\) ফ্রি পাওয়ার পরে কোনও পণ্য কিনবে। নোট করুন যে ওজন \(w_{ij}\) নীতিগতভাবে \(1\) (বা এমনকি নেতিবাচক) এর চেয়েও বেশি হতে পারে, সেই ক্ষেত্রে যেখানে পৃথক \(j\) একাধিক পণ্য কেনে। মোট কেনার সম্ভাব্যতা সর্বাধিকীকরণ মোট ভবিষ্যতের আয়কে সর্বাধিক করার সাথে মিলে যায়। এই মডেলটির একটি বর্ধনের সাথে নোডগুলি ওজন বহন করে, যা আমাদের বিপণনের মডেল হিসাবে বিবেচনা করা যেতে পারে, সম্ভাবনা হিসাবে পণ্যটির একটি নিখরচায় নমুনা দেওয়া কোনও ব্যক্তি ভবিষ্যতে আবার কিনবে। আমাদের মডেলটিতে এই অতিরিক্ত তথ্য সহ, সর্বাধিকীকরণের অব্জেক্টিভ ফাংশনটি হয়ে ওঠে।

\[C(\textbf{x}) = \sum_{i,j} w_{ij} x_i (1-x_j)+\sum_i w_i x_i ।\]

কোয়ান্টাম কম্পিউটারে এই সমস্যার সমাধানের জন্য, প্রথমে একটি আইসিং হ্যামিলটনিয়ানকে এটির ম্যাপিং করা উচিত। এটি অ্যাসাইনমেন্ট \(x_i\rightarrow (1-Z_i)/2\) সহ করা যেতে পারে, যেখানে \(Z_i\) i হ’ল পাওলি Z অপারেটর যার আইগেনভ্যালু \(\pm 1\)। এটি করে আমরা এটি খুঁজে পাই

\[C(\textbf{Z}) = \sum_{i,j} \frac{w_{ij}}{4} (1-Z_i)(1+Z_j) + \sum_i \frac{w_i}{2} (1-Z_i) = -\frac{1}{2}\left( \sum_{i<j} w_{ij} Z_i Z_j +\sum_i w_i Z_i\right)+\mathrm{const},\]

যেখানে :math:`mathrm{const} = sum_{i<j}w_{ij}/2+sum_i w_i/2। অন্য কথায়, ওয়েটেড সর্বোচ্চ লাভ সমস্যাটি আইসিং হ্যামিলটনিয়ানকে হ্রাস করার সমতুল্য

\[H = \sum_i w_i Z_i + \sum_{i<j} w_{ij} Z_iZ_j.\]

Qiskit optimization module can generate the Ising Hamiltonian for the first profit function \(\tilde{C}\). To this extent, function \(\tilde{C}\) can be modeled as a QuadraticProgram, which provides the to_ising() method.

অপ্টিমাইজেশন সমস্যার জন্য আনুমানিক ইউনিভার্সাল কোয়ান্টাম কম্পিউটিং

সমাবেশীয় অনুকূলায়ন (অপ্টিমাইজেশন) সমস্যাসমূহর সমাধানের জন্য কোয়ান্টাম কম্পিউটার ব্যবহার সম্পর্কে সাম্প্রতিক সময়ে যথেষ্ট পরিমাণে আগ্রহ তৈরি হয়েছে। বলা বাহুল্য যে, সমাবেশ সমস্যাগুলির প্রথাগত (ক্লাসিক্যাল) প্রকৃতির পরিপ্রেক্ষিতে, সর্বোত্তম প্রথাগত (ক্লাসিক্যাল) অ্যালগরিদমের তুলনায় কোয়ান্টাম কম্পিউটার ব্যবহারে সূচকীয় গতির গ্যারান্টি নেই। যাইহোক, লক্ষ্য (টার্গেট) সমস্যার প্রকৃতি এবং গুরুত্বের কারণে, এটি কোয়ান্টাম কম্পিউটারে হিউরিস্টিক পন্থাগুলি তদন্তের জন্য মূল্যবান যা প্রকৃতপক্ষে কিছু সমস্যাগুলির উদাহরণগুলিকে গতিতে পারে। এখানে আমরা এমন একটি পদ্ধতির প্রদর্শন করি যা ফারহি, গোল্ডস্টোন এবং গুটম্যান (২০১৪) দ্বারা কোয়ান্টাম আনুমানিক অপ্টিমাইজেশন অ্যালগরিদম (কিউ.এ.ও.এ.) এর উপর ভিত্তি করে। আমরা আলগরিদমকে আনুমানিক কোয়ান্টাম কম্পিউটিং এর প্রাসঙ্গিক আকারে এর ফ্রেমযুক্ত প্রকৃতির উপর ভিত্তি করে ফ্রেম করি।

অ্যালগরিদম টি নিম্নলিখিত উপায়ে কাজ করে :

1. টার্গেট আইসিং সমস্যা: \(w_i\) এবং \(w_{ij}\) চয়ন করুন। নীতিগতভাবে, Z-র উচ্চতর ক্ষমতাগুলিও অনুমোদিত।

2. কোয়ান্টাম সার্কিট :math:`m -র গভীরতা চয়ন করুন। টীকা: গভীরতাটি অভিযোজিতভাবে সংশোধন করা যেতে পারে।.

3. কনট্রোল \(\theta\) এর একটি সেট চয়ন করুন এবং সি-ফেজ ( C-Phase ) গেটস এবং একক কিউবিট ওয়াই (Y) রোটেশনগুলির তৈরি কোয়ান্টাম সার্কিট ব্যবহার করে তৈরি করে ট্রায়াল ফাংশন \(|\psi(\boldsymbol\theta)\rangle\) করুন, যা \(\boldsymbol\theta\) এর উপাদানগুলি দ্বারা প্যারামিটারাইজড |

4. মূল্যায়ন

   \[C(\boldsymbol\theta) = \langle\psi(\boldsymbol\theta)~|H|~\psi(\boldsymbol\theta)\rangle = \sum_i w_i \langle\psi(\boldsymbol\theta)~|Z_i|~\psi(\boldsymbol\theta)\rangle+ \sum_{i<j} w_{ij} \langle\psi(\boldsymbol\theta)~|Z_iZ_j|~\psi(\boldsymbol\theta)\rangle\]

   জেড-বেসিস সার্কিটের ফলাফল নমুনা করে এবং পৃথক আইসিং পদগুলির প্রত্যাশা মানগুলি একসাথে যুক্ত করে। সাধারণভাবে, নির্বাচিত প্রথাগত (ক্লাসিক্যাল) অনুকূলায়ক এর উপর নির্ভর করে, :math:`boldsymboltheta এর চারপাশের বিভিন্ন নিয়ন্ত্রণ পয়েন্টগুলি অনুমান করতে হবে।

5. নতুন সেট নিয়ন্ত্রণ চয়ন করতে একটি প্রথাগত (ক্লাসিক্যাল) অনুকূলায়ক বা অপ্টিমাইজার ব্যবহার করুন।.

6. যতক্ষণ না \(C(\boldsymbol\theta)\) ন্যূনতমে পৌঁছে যায়, যা কিনা \(\boldsymbol\theta^*\) সমাধানের জন্য খুব কাছাকাছি, ততক্ষন চালিয়ে যান।

7. শেষ \(\boldsymbol\theta\) ব্যবহার করুন \(\Big|\langle z_i\big|\psi(\boldsymbol\theta)\rangle\Big|^2\;\forall i\) বণ্টন থেকে অন্তিম নমুনা (স্যাম্পল) সমূহ উৎপন্ন করে উত্তর পাওয়ার জন্যে।

এটি আমাদের বিশ্বাস যে ভাল হিউরিস্টিক অ্যালগরিদমগুলি খুঁজে পেতে অসুবিধাটি একটি উপযুক্ত ট্রায়াল ওয়েভ ফাংশন পছন্দে একীভূত হবে। উদাহরণস্বরূপ, কেউ একটি ট্রায়াল ফাংশন বিবেচনা করতে পারে যার এনট্যাঙ্গেলমেন্ট, লক্ষ্য সমস্যাটির সাথে সর্বোত্তমভাবে প্রান্তিক হয় বা কেবল এনট্যাঙ্গেলমেন্ট হওয়ার পরিমাণকে পরিবর্তনশীল করে তোলে। এই টিউটোরিয়ালে, আমরা ফর্মটির একটি সাধারণ ট্রায়াল ফাংশন বিবেচনা করব

\[|\psi(\theta)\rangle = [U_\mathrm{single}(\boldsymbol\theta) U_\mathrm{entangler}]^m |+\rangle\]

যেখানে \(U_\mathrm{entangler}\) হল সি-ফেজ গেটস (সম্পূর্ণরূপে এনট্যাঙ্গেল বা পরিসাংখ্যিক যোগাযোগ বা বিজড়িত দরজা) এবং \(U_\mathrm{single}(\theta) = \prod_{i=1}^n Y(\theta_{i})\), যেখানে \(n\) কিউবিট সংখ্যা এবং \(m\) কোয়ান্টাম সার্কিটের গভীরতা। এই পছন্দটির অনুপ্রেরণা হ’ল, এই প্রথাগত (ক্লাসিক্যাল) সমস্যার জন্য এটি কোয়ান্টাম স্টেটের যে স্থানগুলিতে কেবল প্রকৃত সহগ রয়েছে তার সন্ধানের অনুমতি দেয়, তবুও সম্ভাব্যভাবে সমাধানে আরও দ্রুত রূপান্তরিত করতে এনট্যাঙ্গেলমেন্ট প্রবণতাটিকে কাজে লাগিয়ে।

অ্যাডিয়াব্যাটিক পদ্ধতির তুলনায় এই স্যাম্পলিং পদ্ধতিটি ব্যবহার করার একটি সুবিধা হল টার্গেট আইসিং হ্যামিল্টনিয়ানকে সরাসরি হার্ডওয়্যারে প্রয়োগ করা উচিত নয়, এই অ্যালগরিদমটিকে ডিভাইসের সংযোগের মধ্যে সীমাবদ্ধ না। তদুপরি, ব্যয় কার্যক্রমে উচ্চতর অর্ডার শর্তাদি, যেমন :math:`Z_iZ_jZ_k , এগুলিও দক্ষতার সাথে নমুনাযুক্ত করা যেতে পারে, যেখানে অ্যাডিয়াব্যাটিক বা অ্যানিলিং পদ্ধতির ক্ষেত্রে তারা সাধারণত মোকাবেলা করতে অযৌক্তিক হয়।

References:

•  A. Lucas, Frontiers in Physics 2, 5 (2014)

•  E. Farhi, J. Goldstone, S. Gutmann, e-print arXiv 1411.4028 (2014)

•  D. Wecker, M. B. Hastings, M. Troyer, Phys. Rev. A 94, 022309 (2016)

•  E. Farhi, J. Goldstone, S. Gutmann, H. Neven, e-print arXiv 1703.06199 (2017)

অ্যাপ্লিকেশন ক্লাস

আমরা সর্বোচ্চ লাভ সমস্যা ও ভ্রাম্যমান বিক্রেতার সমস্যার জন্য অ্যাপ্লিকেশন ক্লাস ব্যবহার করতে পারি। অন্যান্য অনুকূলায়ন (অপ্টিমাইজেশন) সমস্যাসমূহর জন্য আরো অ্যাপ্লিকেশন ক্লাস আছে। বিস্তারিত জানতে Application Classes for Optimization Problems দেখ।

# useful additional packages
import matplotlib.pyplot as plt
import numpy as np
import networkx as nx

from qiskit.tools.visualization import plot_histogram
from qiskit.circuit.library import TwoLocal
from qiskit_optimization.applications import Maxcut, Tsp
from qiskit_algorithms import SamplingVQE, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import SPSA
from qiskit_algorithms.utils import algorithm_globals
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import MinimumEigenOptimizer

সর্বোচ্চ লাভ সমস্যা (Max-Cut problem)

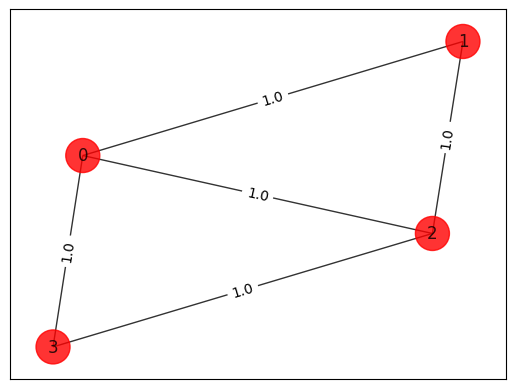
# Generating a graph of 4 nodes

n = 4  # Number of nodes in graph
G = nx.Graph()
G.add_nodes_from(np.arange(0, n, 1))
elist = [(0, 1, 1.0), (0, 2, 1.0), (0, 3, 1.0), (1, 2, 1.0), (2, 3, 1.0)]
# tuple is (i,j,weight) where (i,j) is the edge
G.add_weighted_edges_from(elist)

colors = ["r" for node in G.nodes()]
pos = nx.spring_layout(G)


def draw_graph(G, colors, pos):
    default_axes = plt.axes(frameon=True)
    nx.draw_networkx(G, node_color=colors, node_size=600, alpha=0.8, ax=default_axes, pos=pos)
    edge_labels = nx.get_edge_attributes(G, "weight")
    nx.draw_networkx_edge_labels(G, pos=pos, edge_labels=edge_labels)


draw_graph(G, colors, pos)

# Computing the weight matrix from the random graph
w = np.zeros([n, n])
for i in range(n):
    for j in range(n):
        temp = G.get_edge_data(i, j, default=0)
        if temp != 0:
            w[i, j] = temp["weight"]
print(w)

[[0. 1. 1. 1.]
 [1. 0. 1. 0.]
 [1. 1. 0. 1.]
 [1. 0. 1. 0.]]

ব্রুট ফোর্স পদ্ধতি

সমস্ত সম্ভাব্য \(2^n সমন্বয় চেষ্টা করুন। যেমন :math:`n = 4\), উদাহরণস্বরূপ, একজন কেবলমাত্র 16 টি সংমিশ্রণের সাথে ডিল করে তবে n = 1000 এর জন্য একটিতে 1.071509e + 30 সংমিশ্রণ রয়েছে, যা ব্রুট ফোর্স পদ্ধতির ব্যবহার করে মোকাবেলা করা অযৌক্তিক।

best_cost_brute = 0
for b in range(2**n):
    x = [int(t) for t in reversed(list(bin(b)[2:].zfill(n)))]
    cost = 0
    for i in range(n):
        for j in range(n):
            cost = cost + w[i, j] * x[i] * (1 - x[j])
    if best_cost_brute < cost:
        best_cost_brute = cost
        xbest_brute = x
    print("case = " + str(x) + " cost = " + str(cost))

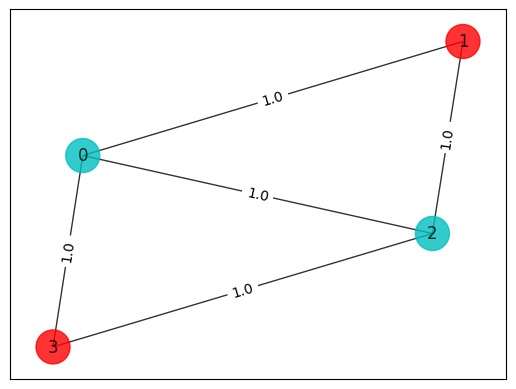
colors = ["r" if xbest_brute[i] == 0 else "c" for i in range(n)]
draw_graph(G, colors, pos)
print("\nBest solution = " + str(xbest_brute) + " cost = " + str(best_cost_brute))

case = [0, 0, 0, 0] cost = 0.0
case = [1, 0, 0, 0] cost = 3.0
case = [0, 1, 0, 0] cost = 2.0
case = [1, 1, 0, 0] cost = 3.0
case = [0, 0, 1, 0] cost = 3.0
case = [1, 0, 1, 0] cost = 4.0
case = [0, 1, 1, 0] cost = 3.0
case = [1, 1, 1, 0] cost = 2.0
case = [0, 0, 0, 1] cost = 2.0
case = [1, 0, 0, 1] cost = 3.0
case = [0, 1, 0, 1] cost = 4.0
case = [1, 1, 0, 1] cost = 3.0
case = [0, 0, 1, 1] cost = 3.0
case = [1, 0, 1, 1] cost = 2.0
case = [0, 1, 1, 1] cost = 3.0
case = [1, 1, 1, 1] cost = 0.0

Best solution = [1, 0, 1, 0] cost = 4.0

আইসিং সমস্যার ম্যাপিং (চিত্রায়ন)

Qiskit optimization provides functionality to generate QuadraticProgram from the problem specification as well as create the corresponding Ising Hamiltonian.

max_cut = Maxcut(w)
qp = max_cut.to_quadratic_program()
print(qp.prettyprint())

Problem name: Max-cut

Maximize
  -2*x_0*x_1 - 2*x_0*x_2 - 2*x_0*x_3 - 2*x_1*x_2 - 2*x_2*x_3 + 3*x_0 + 2*x_1
  + 3*x_2 + 2*x_3

Subject to
  No constraints

  Binary variables (4)
    x_0 x_1 x_2 x_3

qubitOp, offset = qp.to_ising()
print("Offset:", offset)
print("Ising Hamiltonian:")
print(str(qubitOp))

Offset: -2.5
Ising Hamiltonian:
SparsePauliOp(['IIZZ', 'IZIZ', 'IZZI', 'ZIIZ', 'ZZII'],
              coeffs=[0.5+0.j, 0.5+0.j, 0.5+0.j, 0.5+0.j, 0.5+0.j])

# solving Quadratic Program using exact classical eigensolver
exact = MinimumEigenOptimizer(NumPyMinimumEigensolver())
result = exact.solve(qp)
print(result.prettyprint())

objective function value: 4.0
variable values: x_0=1.0, x_1=0.0, x_2=1.0, x_3=0.0
status: SUCCESS

যেহেতু সমস্যাটি একটি মিনিমাইজেশন সমস্যার জন্য ফেলে দেওয়া হয়েছিল, তাই \(-4\) সমাধানটি সর্বোত্তমের সাথে মিলে যায়।.

সম্পূর্ণ হ্যামিল্টোনিয়ান সঠিক ব্যয় দেয় তা পরীক্ষা করা হচ্ছে

# Making the Hamiltonian in its full form and getting the lowest eigenvalue and eigenvector
ee = NumPyMinimumEigensolver()
result = ee.compute_minimum_eigenvalue(qubitOp)

x = max_cut.sample_most_likely(result.eigenstate)
print("energy:", result.eigenvalue.real)
print("max-cut objective:", result.eigenvalue.real + offset)
print("solution:", x)
print("solution objective:", qp.objective.evaluate(x))

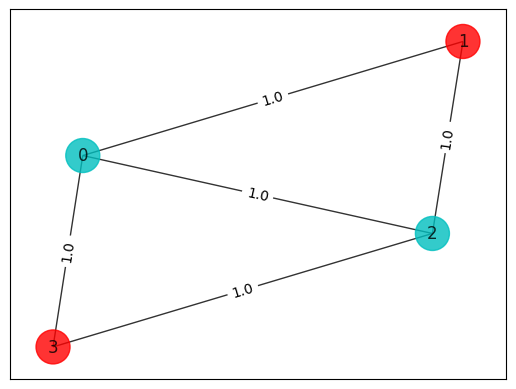
colors = ["r" if x[i] == 0 else "c" for i in range(n)]
draw_graph(G, colors, pos)

energy: -1.5
max-cut objective: -4.0
solution: [1. 0. 1. 0.]
solution objective: 4.0

কোয়ান্টাম কম্পিউটারে চালানো

আমরা কোয়ান্টাম কম্পিউটারের সাথে ফিডব্যাক লুপ ব্যবহার করে অপ্টিমাইজেশন রুটিন চালাই যা Y একক-কিউবিট ঘূর্ণন, \(U_\mathrm{single}(\theta) = \prod_{i=1}^n Y(\theta_{i})\), এবং এন্ট্যাঙ্গলারের ধাপগুলি \(U_\mathrm{entangler}\) এর সাহায্যে নির্মিত ট্রায়াল ফাংশন ব্যবহার করে।

algorithm_globals.random_seed = 123
seed = 10598

# construct SamplingVQE
optimizer = SPSA(maxiter=300)
ry = TwoLocal(qubitOp.num_qubits, "ry", "cz", reps=5, entanglement="linear")
vqe = SamplingVQE(sampler=Sampler(), ansatz=ry, optimizer=optimizer)

# run SamplingVQE
result = vqe.compute_minimum_eigenvalue(qubitOp)

# print results
x = max_cut.sample_most_likely(result.eigenstate)
print("energy:", result.eigenvalue.real)
print("time:", result.optimizer_time)
print("max-cut objective:", result.eigenvalue.real + offset)
print("solution:", x)
print("solution objective:", qp.objective.evaluate(x))

# plot results
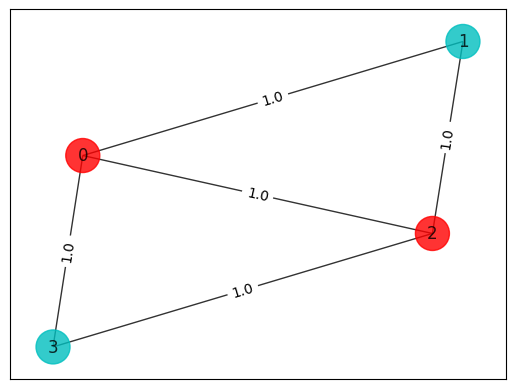
colors = ["r" if x[i] == 0 else "c" for i in range(n)]
draw_graph(G, colors, pos)

energy: -1.4996861455587311
time: 8.708028078079224
max-cut objective: -3.999686145558731
solution: [0 1 0 1]
solution objective: 4.0

# create minimum eigen optimizer based on SamplingVQE
vqe_optimizer = MinimumEigenOptimizer(vqe)

# solve quadratic program
result = vqe_optimizer.solve(qp)
print(result.prettyprint())

colors = ["r" if result.x[i] == 0 else "c" for i in range(n)]
draw_graph(G, colors, pos)

objective function value: 4.0
variable values: x_0=1.0, x_1=0.0, x_2=1.0, x_3=0.0
status: SUCCESS

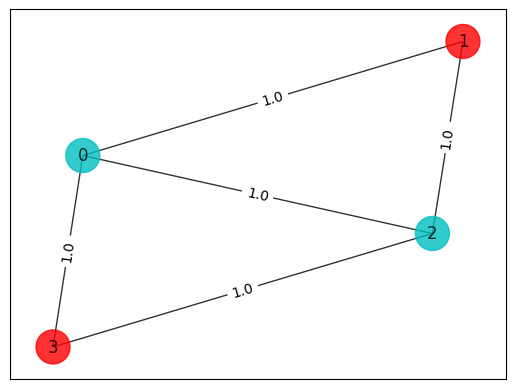
ট্রাভেলিং সেলসম্যান সমস্যা

In addition to being a notorious NP-complete problem that has drawn the attention of computer scientists and mathematicians for over two centuries, the Traveling Salesman Problem (TSP) has important bearings on finance and marketing, as its name suggests. Colloquially speaking, the traveling salesman is a person that goes from city to city to sell merchandise. The objective in this case is to find the shortest path that would enable the salesman to visit all the cities and return to its hometown, i.e. the city where he started traveling. By doing this, the salesman gets to maximize potential sales in the least amount of time.

The problem derives its importance from its "hardness" and ubiquitous equivalence to other relevant combinatorial optimization problems that arise in practice.

কিছু প্রাথমিক বিশ্লেষণের সাথে গাণিতিক সূত্রটি ডাব্লু.আর. হ্যামিল্টন ১৯ শতকের গোড়ার দিকে প্রস্তাব করেছিলেন। গাণিতিকভাবে সমস্যাটি হ’ল ম্যাক্স-কাটের গ্রাফের ক্ষেত্রে সবচেয়ে ভাল বিমূর্ত। কোনও গ্রাফের নোডের টিএসপি সর্বনিম্ন * হ্যামিলটোনিয়ান চক্র * যা প্রতিটি নোডের মধ্য দিয়ে নেওয়া যায় তা জিজ্ঞাসা করে। একটি হ্যামিল্টোনিয়ান চক্র এমন একটি বদ্ধ পথ যা একবারে গ্রাফের প্রতিটি প্রান্তকে একবার ব্যবহার করে। সাধারণ সমাধানটি অজানা এবং একটি অ্যালগরিদম (উদাঃ, বহু-কালীন সময়ে) এর উপস্থিতি প্রত্যাশিত নয় যা কার্যকরভাবে এটি খুঁজে পায় ।

Find the shortest Hamiltonian cycle in a graph \(G=(V,E)\) with \(n=|V|\) nodes and distances, \(w_{ij}\) (distance from vertex \(i\) to vertex \(j\)). A Hamiltonian cycle is described by \(N^2\) variables \(x_{i,p}\), where \(i\) represents the node and \(p\) represents its order in a prospective cycle. The decision variable takes the value 1 if the solution occurs at node \(i\) at time order \(p\). We require that every node can only appear once in the cycle, and for each time a node has to occur. This amounts to the two constraints (here and in the following, whenever not specified, the summands run over 0,1,…N-1)

\[\sum_{i} x_{i,p} = 1 ~~\forall p\]

\[\sum_{p} x_{i,p} = 1 ~~\forall i।\]

আমাদের সম্ভাব্য ক্রমান্বয়ে নোডের জন্য, \(x_{i,p}\) এবং \(x_{j,p+1}\) উভয়ই যদি ১ হয় তবে সেখানে শক্তির জরিমানা থাকতে হবে যদি: \((i,j) \notin E\) (গ্রাফের সাথে সংযুক্ত নয়)। এই জরিমানার ফর্মটি হ’ল

\[\sum_{i,j\notin E}\sum_{p} x_{i,p}x_{j,p+1}>0,\]

যেখানে এটি হ্যামিল্টোনিয়ান চক্র \((p=N)\equiv (p=0)\) সীমানা শর্ত হিসাবে ধরে নেওয়া হয়। তবে, এখানে এটি সম্পূর্ণ সংযুক্ত গ্রাফ হিসাবে ধরে নেওয়া হবে এবং এই পদটি অন্তর্ভুক্ত করা হবে না। যে দূরত্বটি হ্রাস করা দরকার তা হ’ল

\[C(\textbf{x})=\sum_{i,j}w_{ij}\sum_{p} x_{i,p}x_{j,p+1}।\]

এগুলি হ্রাস করতে একটি একক নৈর্ব্যক্তিক অন্বয় (অব্জেক্টিভ ফাংশন) একসাথে রাখলে আমরা নিম্নলিখিতটি পাই:

\[C(\textbf{x})=\sum_{i,j}w_{ij}\sum_{p} x_{i,p}x_{j,p+1}+ A\sum_p\left(1- \sum_i x_{i,p}\right)^2+A\sum_i\left(1- \sum_p x_{i,p}\right)^2,\]

যেখানে \(A\) একটি নিখরচায় প্যারামিটার। একজনকে নিশ্চিত করতে হবে যে \(A\) যথেষ্ট বড় যাতে এই প্রতিবন্ধকতাগুলি সম্মানিত হয়। এটি করার একটি উপায় হ’ল \(A`কে এমন চয়ন করা যাতে :math:`A > \mathrm{max}(w_{ij})\) ।

আবারও, এই আকারে সমস্যাটি একটি কোয়ান্টাম কম্পিউটারে ম্যাপ করা সহজ, এবং একটি আইসিং হ্যামিলটনিয়ানকে হ্রাস করে সমাধানটি পাওয়া যাবে।

# Generating a graph of 3 nodes
n = 3
num_qubits = n**2
tsp = Tsp.create_random_instance(n, seed=123)
adj_matrix = nx.to_numpy_array(tsp.graph)
print("distance\n", adj_matrix)

colors = ["r" for node in tsp.graph.nodes]
pos = [tsp.graph.nodes[node]["pos"] for node in tsp.graph.nodes]
draw_graph(tsp.graph, colors, pos)

distance
 [[ 0. 48. 91.]
 [48.  0. 63.]
 [91. 63.  0.]]

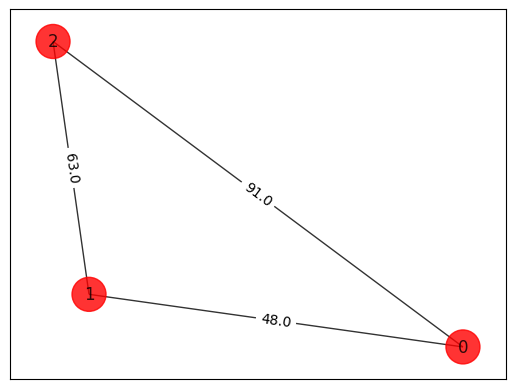
ব্রুট ফোর্স পদ্ধতি

from itertools import permutations


def brute_force_tsp(w, N):
    a = list(permutations(range(1, N)))
    last_best_distance = 1e10
    for i in a:
        distance = 0
        pre_j = 0
        for j in i:
            distance = distance + w[j, pre_j]
            pre_j = j
        distance = distance + w[pre_j, 0]
        order = (0,) + i
        if distance < last_best_distance:
            best_order = order
            last_best_distance = distance
            print("order = " + str(order) + " Distance = " + str(distance))
    return last_best_distance, best_order


best_distance, best_order = brute_force_tsp(adj_matrix, n)
print(
    "Best order from brute force = "
    + str(best_order)
    + " with total distance = "
    + str(best_distance)
)


def draw_tsp_solution(G, order, colors, pos):
    G2 = nx.DiGraph()
    G2.add_nodes_from(G)
    n = len(order)
    for i in range(n):
        j = (i + 1) % n
        G2.add_edge(order[i], order[j], weight=G[order[i]][order[j]]["weight"])
    default_axes = plt.axes(frameon=True)
    nx.draw_networkx(
        G2, node_color=colors, edge_color="b", node_size=600, alpha=0.8, ax=default_axes, pos=pos
    )
    edge_labels = nx.get_edge_attributes(G2, "weight")
    nx.draw_networkx_edge_labels(G2, pos, font_color="b", edge_labels=edge_labels)


draw_tsp_solution(tsp.graph, best_order, colors, pos)

order = (0, 1, 2) Distance = 202.0
Best order from brute force = (0, 1, 2) with total distance = 202.0

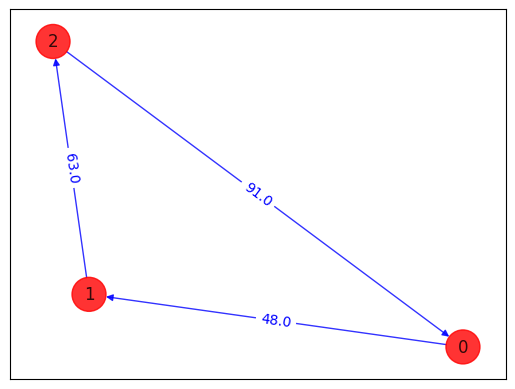
আইসিং সমস্যার ম্যাপিং (চিত্রায়ন)

qp = tsp.to_quadratic_program()
print(qp.prettyprint())

Problem name: TSP

Minimize
  48*x_0_0*x_1_1 + 48*x_0_0*x_1_2 + 91*x_0_0*x_2_1 + 91*x_0_0*x_2_2
  + 48*x_0_1*x_1_0 + 48*x_0_1*x_1_2 + 91*x_0_1*x_2_0 + 91*x_0_1*x_2_2
  + 48*x_0_2*x_1_0 + 48*x_0_2*x_1_1 + 91*x_0_2*x_2_0 + 91*x_0_2*x_2_1
  + 63*x_1_0*x_2_1 + 63*x_1_0*x_2_2 + 63*x_1_1*x_2_0 + 63*x_1_1*x_2_2
  + 63*x_1_2*x_2_0 + 63*x_1_2*x_2_1

Subject to
  Linear constraints (6)
    x_0_0 + x_0_1 + x_0_2 == 1  'c0'
    x_1_0 + x_1_1 + x_1_2 == 1  'c1'
    x_2_0 + x_2_1 + x_2_2 == 1  'c2'
    x_0_0 + x_1_0 + x_2_0 == 1  'c3'
    x_0_1 + x_1_1 + x_2_1 == 1  'c4'
    x_0_2 + x_1_2 + x_2_2 == 1  'c5'

  Binary variables (9)
    x_0_0 x_0_1 x_0_2 x_1_0 x_1_1 x_1_2 x_2_0 x_2_1 x_2_2

from qiskit_optimization.converters import QuadraticProgramToQubo

qp2qubo = QuadraticProgramToQubo()
qubo = qp2qubo.convert(qp)
qubitOp, offset = qubo.to_ising()
print("Offset:", offset)
print("Ising Hamiltonian:")
print(str(qubitOp))

Offset: 7581.0
Ising Hamiltonian:
SparsePauliOp(['IIIIIIIIZ', 'IIIIIIIZI', 'IIIIIIZII', 'IIIIIZIII', 'IIIIZIIII', 'IIIZIIIII', 'IIZIIIIII', 'IZIIIIIII', 'ZIIIIIIII', 'IIIIIIIZZ', 'IIIIIIZIZ', 'IIIIIIZZI', 'IIIIIZIIZ', 'IIIIIZIZI', 'IIIIIZZII', 'IIIIZIIIZ', 'IIIIZIIZI', 'IIIIZIZII', 'IIIIZZIII', 'IIIZIIIIZ', 'IIIZIIIZI', 'IIIZIIZII', 'IIIZIZIII', 'IIIZZIIII', 'IIZIIIIIZ', 'IIZIIIIZI', 'IIZIIIZII', 'IIZIIZIII', 'IIZIZIIII', 'IIZZIIIII', 'IZIIIIIIZ', 'IZIIIIIZI', 'IZIIIIZII', 'IZIIIZIII', 'IZIIZIIII', 'IZIZIIIII', 'IZZIIIIII', 'ZIIIIIIIZ', 'ZIIIIIIZI', 'ZIIIIIZII', 'ZIIIIZIII', 'ZIIIZIIII', 'ZIIZIIIII', 'ZIZIIIIII', 'ZZIIIIIII'],
              coeffs=[-1282.5 +0.j, -1282.5 +0.j, -1282.5 +0.j, -1268.5 +0.j, -1268.5 +0.j,
 -1268.5 +0.j, -1290.  +0.j, -1290.  +0.j, -1290.  +0.j,   606.5 +0.j,
   606.5 +0.j,   606.5 +0.j,   606.5 +0.j,    12.  +0.j,    12.  +0.j,
    12.  +0.j,   606.5 +0.j,    12.  +0.j,   606.5 +0.j,    12.  +0.j,
    12.  +0.j,   606.5 +0.j,   606.5 +0.j,   606.5 +0.j,   606.5 +0.j,
    22.75+0.j,    22.75+0.j,   606.5 +0.j,    15.75+0.j,    15.75+0.j,
    22.75+0.j,   606.5 +0.j,    22.75+0.j,    15.75+0.j,   606.5 +0.j,
    15.75+0.j,   606.5 +0.j,    22.75+0.j,    22.75+0.j,   606.5 +0.j,
    15.75+0.j,    15.75+0.j,   606.5 +0.j,   606.5 +0.j,   606.5 +0.j])

result = exact.solve(qubo)
print(result.prettyprint())

objective function value: 202.0
variable values: x_0_0=1.0, x_0_1=0.0, x_0_2=0.0, x_1_0=0.0, x_1_1=1.0, x_1_2=0.0, x_2_0=0.0, x_2_1=0.0, x_2_2=1.0
status: SUCCESS

সম্পূর্ণ হ্যামিল্টোনিয়ান সঠিক ব্যয় দেয় তা পরীক্ষা করা হচ্ছে

# Making the Hamiltonian in its full form and getting the lowest eigenvalue and eigenvector
ee = NumPyMinimumEigensolver()
result = ee.compute_minimum_eigenvalue(qubitOp)

print("energy:", result.eigenvalue.real)
print("tsp objective:", result.eigenvalue.real + offset)
x = tsp.sample_most_likely(result.eigenstate)
print("feasible:", qubo.is_feasible(x))
z = tsp.interpret(x)
print("solution:", z)
print("solution objective:", tsp.tsp_value(z, adj_matrix))
draw_tsp_solution(tsp.graph, z, colors, pos)

energy: -7379.0
tsp objective: 202.0
feasible: True
solution: [0, 1, 2]
solution objective: 202.0

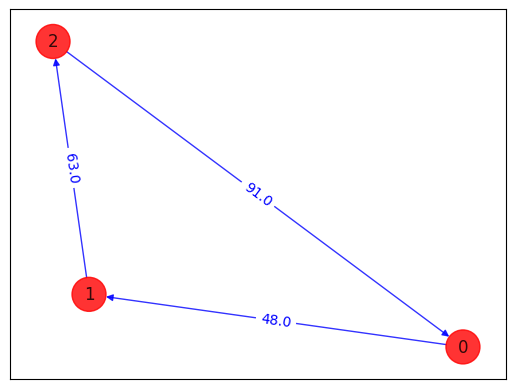
কোয়ান্টাম কম্পিউটারে চালানো

আমরা কোয়ান্টাম কম্পিউটারের সাথে ফিডব্যাক লুপ ব্যবহার করে অপ্টিমাইজেশন রুটিন চালাই যা Y একক-কিউবিট ঘূর্ণন, \(U_\mathrm{single}(\theta) = \prod_{i=1}^n Y(\theta_{i})\), এবং এন্ট্যাঙ্গলারের ধাপগুলি \(U_\mathrm{entangler}\) এর সাহায্যে নির্মিত ট্রায়াল ফাংশন ব্যবহার করে।

algorithm_globals.random_seed = 123
seed = 10598

optimizer = SPSA(maxiter=300)
ry = TwoLocal(qubitOp.num_qubits, "ry", "cz", reps=5, entanglement="linear")
vqe = SamplingVQE(sampler=Sampler(), ansatz=ry, optimizer=optimizer)

result = vqe.compute_minimum_eigenvalue(qubitOp)

print("energy:", result.eigenvalue.real)
print("time:", result.optimizer_time)
x = tsp.sample_most_likely(result.eigenstate)
print("feasible:", qubo.is_feasible(x))
z = tsp.interpret(x)
print("solution:", z)
print("solution objective:", tsp.tsp_value(z, adj_matrix))
draw_tsp_solution(tsp.graph, z, colors, pos)

energy: -7326.024699521861
time: 28.526036977767944
feasible: True
solution: [1, 2, 0]
solution objective: 202.0

algorithm_globals.random_seed = 123
seed = 10598

# create minimum eigen optimizer based on SamplingVQE
vqe_optimizer = MinimumEigenOptimizer(vqe)

# solve quadratic program
result = vqe_optimizer.solve(qp)
print(result.prettyprint())

z = tsp.interpret(x)
print("solution:", z)
print("solution objective:", tsp.tsp_value(z, adj_matrix))
draw_tsp_solution(tsp.graph, z, colors, pos)

objective function value: 202.0
variable values: x_0_0=0.0, x_0_1=0.0, x_0_2=1.0, x_1_0=1.0, x_1_1=0.0, x_1_2=0.0, x_2_0=0.0, x_2_1=1.0, x_2_2=0.0
status: SUCCESS
solution: [1, 2, 0]
solution objective: 202.0

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
qiskit-terra	0.25.0.dev0+1d844ec
qiskit-aer	0.12.0
qiskit-ibmq-provider	0.20.2
qiskit-nature	0.7.0
qiskit-optimization	0.6.0
System information
Python version	3.10.11
Python compiler	Clang 14.0.0 (clang-1400.0.29.202)
Python build	main, Apr 7 2023 07:31:31
OS	Darwin
CPUs	4
Memory (Gb)	16.0
Thu May 18 16:57:58 2023 JST

This code is a part of Qiskit

© Copyright IBM 2017, 2023.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.