Nota

Esta página fue generada a partir de docs/tutorials/06_examples_max_cut_and_tsp.ipynb.

Max-Cut y Problema del Vendedor Viajero#

Introducción#

Muchos problemas en campos cuantitativos como las finanzas y la ingeniería son problemas de optimización. Los problemas de optimización se encuentran en el centro de la compleja toma de decisiones y la definición de estrategias.

Optimización (u optimización combinatoria) significa buscar una solución óptima en un conjunto finito o contablemente infinito de soluciones potenciales. La optimalidad se define con respecto a alguna función de criterio, que debe minimizarse o maximizarse. Esto normalmente se llama función de costo o función objetivo.

Problemas típicos de optimización

Minimización: costo, distancia, longitud de un recorrido, peso, tiempo de procesamiento, material, consumo de energía, número de objetos

Maximización: beneficio, valor, producción, retorno, rendimiento, utilidad, eficiencia, capacidad, número de objetos

Consideramos aquí problemas de máximo corte (max-cut) de interés práctico en muchos campos, y mostramos cómo se pueden mapear manualmente en computadoras cuánticas y cómo el módulo de optimización de Qiskit lo soporta.

Max-Cut Ponderado#

Max-Cut (máximo corte) es un problema NP completo, con aplicaciones en agrupamiento (clustering), ciencia de redes y física estadística. Para comprender cómo se asignan las aplicaciones prácticas a instancias determinadas de Max-Cut, considera un sistema de muchas personas que pueden interactuar e influir entre sí. Los individuos se pueden representar mediante vértices de un grafo y sus interacciones se pueden ver como conexiones por pares entre vértices del grafo, o aristas. Con esta representación en mente, es fácil modelar los problemas típicos de mercadotecnia. Por ejemplo, supón que se asume que los individuos influirán en las decisiones de compra de los demás, y se da conocimiento sobre que tan fuerte se influirán entre sí. La influencia se puede modelar mediante los pesos asignados en cada arista del grafo. Entonces, es posible predecir el resultado de una estrategia de mercadotecnia en la que los productos se ofrecen de forma gratuita a algunos individuos, y luego preguntar cuál es el subconjunto óptimo de individuos que deberían obtener los productos gratuitos, para maximizar los ingresos.

La definición formal de este problema es la siguiente:

Considera un grafo G = (V, E) no dirigido de \(n\) nodos, donde |V| = n, con pesos de arista \(w_{ij}>0\), \(w_{ij}=w_{ji}\), para \((i, j)\in E\). Un corte se define como una partición del conjunto V original en dos subconjuntos. La función de costo a optimizar es en este caso la suma de los pesos de las aristas que conectan los puntos en los dos subconjuntos diferentes, cruzando el corte. Al asignar \(x_i=0\) o \(x_i=1\) a cada nodo \(i\), se intenta maximizar la función de beneficio global (aquí y en las siguientes sumas los índices corren sobre 0,1,…n-1)

\[\tilde{C}(\textbf{x}) = \sum_{i,j} w_{ij} x_i (1-x_j).\]

En nuestro modelo de mercadotecnia simple, \(w_{ij}\) representa la probabilidad de que la persona \(j\) compre un producto después de que la persona \(i\) obtenga uno gratis. Ten en cuenta que los pesos \(w_{ij}\) pueden, en principio, ser mayores que \(1\) (o incluso negativos), correspondiente al caso en el que el individuo \(j\) comprará más de un producto. Maximizar la probabilidad de compra total corresponde a maximizar los ingresos futuros totales. En el caso de que la probabilidad de ganancia sea mayor que el costo de las muestras gratuitas iniciales, la estrategia es conveniente. Una extensión de este modelo hace que los propios nodos tengan pesos, lo que puede considerarse, en nuestro modelo de mercadotecnia, como la probabilidad de que una persona a la que se le haya otorgado una muestra gratuita del producto lo vuelva a comprar en el futuro. Con esta información adicional en nuestro modelo, la función objetivo para maximizar se convierte en

\[C(\textbf{x}) = \sum_{i,j} w_{ij} x_i (1-x_j)+\sum_i w_i x_i.\]

Para encontrar una solución a este problema en una computadora cuántica, primero es necesario mapearlo a un Hamiltoniano de Ising. Esto se puede hacer con la asignación \(x_i\rightarrow (1-Z_i)/2\), donde \(Z_i\) es el operador Z de Pauli que tiene valores propios \(\pm 1\). Haciendo esto encontramos que

\[C(\textbf{Z}) = \sum_{i,j} \frac{w_{ij}}{4} (1-Z_i)(1+Z_j) + \sum_i \frac{w_i}{2} (1-Z_i) = -\frac{1}{2}\left( \sum_{i<j} w_{ij} Z_i Z_j +\sum_i w_i Z_i\right)+\mathrm{const},\]

donde \(\mathrm{const} = \sum_{i<j}w_{ij}/2+\sum_i w_i/2\). En otros términos, el problema de Max-Cut ponderado es equivalente a minimizar el Hamiltoniano de Ising

\[H = \sum_i w_i Z_i + \sum_{i<j} w_{ij} Z_iZ_j.\]

El módulo de optimización de Qiskit puede generar el Hamiltoniano de Ising para la primera función de ganancias \(\tilde{C}\). En este sentido, la función \(\tilde{C}\) se puede modelar como un QuadraticProgram, que proporciona el método to_ising().

Computación Cuántica Universal Aproximada para Problemas de Optimización#

Ha habido un interés considerable en los últimos tiempos sobre el uso de computadoras cuánticas para encontrar una solución a los problemas de optimización combinatoria. Es importante decir que, dada la naturaleza clásica de los problemas combinatorios, no se garantiza una aceleración exponencial en el uso de computadoras cuánticas en comparación con los mejores algoritmos clásicos. Sin embargo, debido a la naturaleza y la importancia de los problemas objetivo, vale la pena investigar enfoques heurísticos en una computadora cuántica que de hecho podrían acelerar algunos ejemplos de problemas. Aquí demostramos un enfoque que se basa en el Algoritmo Cuántico de Optimización Aproximada (Quantum Approximate Optimization Algorithm, QAOA) de Farhi, Goldstone, y Gutmann (2014). Enmarcamos el algoritmo en el contexto de computación cuántica aproximada, dada su naturaleza heurística.

El algoritmo funciona de la siguiente manera:

Elegir \(w_i\) y \(w_{ij}\) en el problema de Ising objetivo. En principio, se permiten potencias de Z aún mayores.
Elegir la profundidad del circuito cuántico \(m\). Se debe tener en cuenta que la profundidad se puede modificar de forma adaptativa.
Elegir un conjunto de controles \(\theta\) y hacer una función de prueba \(|\psi(\boldsymbol\theta)\rangle\), construida utilizando un circuito cuántico hecho de compuertas C-Phase y rotaciones Y de un solo qubit, parametrizada por los componentes de \(\boldsymbol\theta\).
Evaluar

\[C(\boldsymbol\theta) = \langle\psi(\boldsymbol\theta)~|H|~\psi(\boldsymbol\theta)\rangle = \sum_i w_i \langle\psi(\boldsymbol\theta)~|Z_i|~\psi(\boldsymbol\theta)\rangle+ \sum_{i<j} w_{ij} \langle\psi(\boldsymbol\theta)~|Z_iZ_j|~\psi(\boldsymbol\theta)\rangle\]

muestreando el resultado del circuito en la base Z y sumando los valores esperados de los términos Ising individuales. En general, se deben estimar diferentes puntos de control alrededor de \(\boldsymbol\theta\), dependiendo del optimizador clásico elegido.
Utilizar un optimizador clásico para elegir un nuevo conjunto de controles.
Continuar hasta que \(C(\boldsymbol\theta)\) alcance un mínimo, lo suficientemente cercano a la solución \(\boldsymbol\theta^*\).
Utilizar la última \(\boldsymbol\theta\) para generar un conjunto final de muestras de la distribución \(|\langle z_i~|\psi(\boldsymbol\theta)\rangle|^2\;\forall i\) para obtener la respuesta.

Creemos que la dificultad de encontrar buenos algoritmos heurísticos se reducirá a la elección de una función de onda de prueba adecuada. Por ejemplo, se podría considerar una función de prueba cuyo entrelazamiento se alinee mejor con el problema objetivo, o simplemente hacer que la cantidad de entrelazamiento sea una variable. En este tutorial, consideraremos una función de prueba simple de la forma

\[|\psi(\theta)\rangle = [U_\mathrm{simple}(\boldsymbol\theta) U_\mathrm{entrelazador}]^m |+\rangle\]

donde \(U_\mathrm{entrelazador}\) es una colección de compuertas C-Phase (compuertas completamente entrelazadas), y \(U_\mathrm{simple}(\theta) = \prod_{i=1}^n Y(\theta_{i})\), donde \(n\) es el número de qubits y \(m\) es la profundidad del circuito cuántico. La motivación para esta elección es que para estos problemas clásicos, esta elección nos permite buscar en el espacio de estados cuánticos que solo tienen coeficientes reales, aprovechando el entrelazamiento para converger potencialmente más rápido a la solución.

Una ventaja de utilizar este método de muestreo en comparación con los enfoques adiabáticos es que el Hamiltoniano de Ising objetivo no tiene que implementarse directamente en el hardware, lo que permite que este algoritmo no se limite a la conectividad del dispositivo. Además, los términos de orden superior en la función de costo, como \(Z_iZ_jZ_k\), también se pueden muestrear de manera eficiente, mientras que en los enfoques adiabáticos o de annealing (recocido), generalmente no es práctico tratarlos.

Referencias:

A. Lucas, Frontiers in Physics 2, 5 (2014)
E. Farhi, J. Goldstone, S. Gutmann, e-print arXiv 1411.4028 (2014)
D. Wecker, M. B. Hastings, M. Troyer, Phys. Rev. A 94, 022309 (2016)
E. Farhi, J. Goldstone, S. Gutmann, H. Neven, e-print arXiv 1703.06199 (2017)

Clases de aplicación#

Usamos las clases de aplicación para el problema de máximo corte y el problema del vendedor viajero en esta página. También hay disponibles clases de aplicación para otros problemas de optimización. Consulta Clases de Aplicación para Problemas de Optimización para más detalles.

[1]:

# useful additional packages
import matplotlib.pyplot as plt
import numpy as np
import networkx as nx

from qiskit.tools.visualization import plot_histogram
from qiskit.circuit.library import TwoLocal
from qiskit_optimization.applications import Maxcut, Tsp
from qiskit_algorithms import SamplingVQE, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import SPSA
from qiskit_algorithms.utils import algorithm_globals
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import MinimumEigenOptimizer

Problema de Máximo Corte (Max-Cut)#

[2]:

# Generating a graph of 4 nodes

n = 4  # Number of nodes in graph
G = nx.Graph()
G.add_nodes_from(np.arange(0, n, 1))
elist = [(0, 1, 1.0), (0, 2, 1.0), (0, 3, 1.0), (1, 2, 1.0), (2, 3, 1.0)]
# tuple is (i,j,weight) where (i,j) is the edge
G.add_weighted_edges_from(elist)

colors = ["r" for node in G.nodes()]
pos = nx.spring_layout(G)


def draw_graph(G, colors, pos):
    default_axes = plt.axes(frameon=True)
    nx.draw_networkx(G, node_color=colors, node_size=600, alpha=0.8, ax=default_axes, pos=pos)
    edge_labels = nx.get_edge_attributes(G, "weight")
    nx.draw_networkx_edge_labels(G, pos=pos, edge_labels=edge_labels)


draw_graph(G, colors, pos)

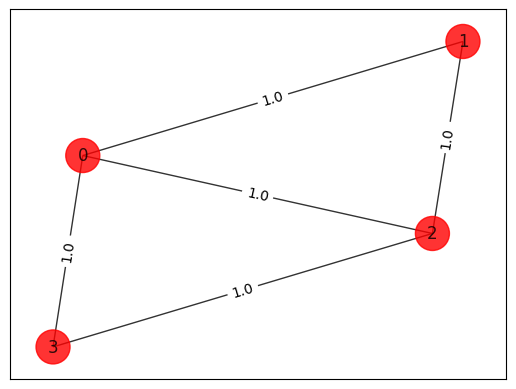
../_images/tutorials_06_examples_max_cut_and_tsp_5_0.png

[3]:

# Computing the weight matrix from the random graph
w = np.zeros([n, n])
for i in range(n):
    for j in range(n):
        temp = G.get_edge_data(i, j, default=0)
        if temp != 0:
            w[i, j] = temp["weight"]
print(w)

[[0. 1. 1. 1.]
 [1. 0. 1. 0.]
 [1. 1. 0. 1.]
 [1. 0. 1. 0.]]

Enfoque de fuerza bruta#

Prueba todas las \(2^n\) combinaciones posibles. Para \(n = 4\), como en este ejemplo, uno trata solo con 16 combinaciones, pero para n = 1000, uno tiene 1.071509e+30 combinaciones, lo cual no es práctico de manejar usando un enfoque de fuerza bruta.

[4]:

best_cost_brute = 0
for b in range(2**n):
    x = [int(t) for t in reversed(list(bin(b)[2:].zfill(n)))]
    cost = 0
    for i in range(n):
        for j in range(n):
            cost = cost + w[i, j] * x[i] * (1 - x[j])
    if best_cost_brute < cost:
        best_cost_brute = cost
        xbest_brute = x
    print("case = " + str(x) + " cost = " + str(cost))

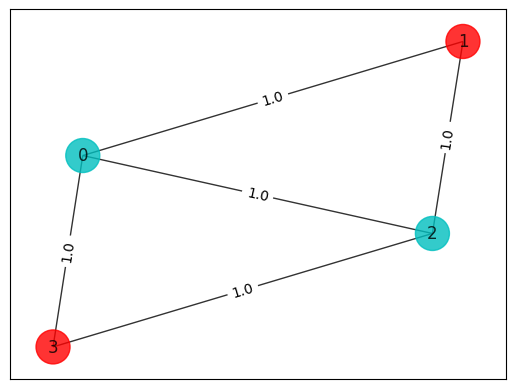
colors = ["r" if xbest_brute[i] == 0 else "c" for i in range(n)]
draw_graph(G, colors, pos)
print("\nBest solution = " + str(xbest_brute) + " cost = " + str(best_cost_brute))

case = [0, 0, 0, 0] cost = 0.0
case = [1, 0, 0, 0] cost = 3.0
case = [0, 1, 0, 0] cost = 2.0
case = [1, 1, 0, 0] cost = 3.0
case = [0, 0, 1, 0] cost = 3.0
case = [1, 0, 1, 0] cost = 4.0
case = [0, 1, 1, 0] cost = 3.0
case = [1, 1, 1, 0] cost = 2.0
case = [0, 0, 0, 1] cost = 2.0
case = [1, 0, 0, 1] cost = 3.0
case = [0, 1, 0, 1] cost = 4.0
case = [1, 1, 0, 1] cost = 3.0
case = [0, 0, 1, 1] cost = 3.0
case = [1, 0, 1, 1] cost = 2.0
case = [0, 1, 1, 1] cost = 3.0
case = [1, 1, 1, 1] cost = 0.0

Best solution = [1, 0, 1, 0] cost = 4.0

../_images/tutorials_06_examples_max_cut_and_tsp_8_1.png

Mapear del problema de Ising#

Qiskit Optimization proporciona funcionalidad para generar el QuadraticProgram a partir de la especificación del problema, así como para crear el correspondiente Hamiltoniano de Ising.

[5]:

max_cut = Maxcut(w)
qp = max_cut.to_quadratic_program()
print(qp.prettyprint())

Problem name: Max-cut

Maximize
  -2*x_0*x_1 - 2*x_0*x_2 - 2*x_0*x_3 - 2*x_1*x_2 - 2*x_2*x_3 + 3*x_0 + 2*x_1
  + 3*x_2 + 2*x_3

Subject to
  No constraints

  Binary variables (4)
    x_0 x_1 x_2 x_3

[6]:

qubitOp, offset = qp.to_ising()
print("Offset:", offset)
print("Ising Hamiltonian:")
print(str(qubitOp))

Offset: -2.5
Ising Hamiltonian:
SparsePauliOp(['IIZZ', 'IZIZ', 'IZZI', 'ZIIZ', 'ZZII'],
              coeffs=[0.5+0.j, 0.5+0.j, 0.5+0.j, 0.5+0.j, 0.5+0.j])

[7]:

# solving Quadratic Program using exact classical eigensolver
exact = MinimumEigenOptimizer(NumPyMinimumEigensolver())
result = exact.solve(qp)
print(result.prettyprint())

objective function value: 4.0
variable values: x_0=1.0, x_1=0.0, x_2=1.0, x_3=0.0
status: SUCCESS

Dado que el problema se convirtió en un problema de minimización, la solución de \(-4\) corresponde al óptimo.

Verificar que el Hamiltoniano completo proporcione el costo correcto#

[8]:

# Making the Hamiltonian in its full form and getting the lowest eigenvalue and eigenvector
ee = NumPyMinimumEigensolver()
result = ee.compute_minimum_eigenvalue(qubitOp)

x = max_cut.sample_most_likely(result.eigenstate)
print("energy:", result.eigenvalue.real)
print("max-cut objective:", result.eigenvalue.real + offset)
print("solution:", x)
print("solution objective:", qp.objective.evaluate(x))

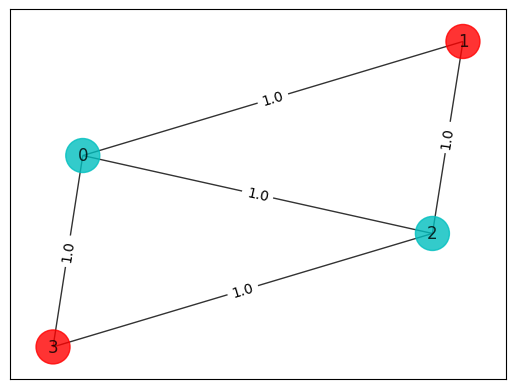
colors = ["r" if x[i] == 0 else "c" for i in range(n)]
draw_graph(G, colors, pos)

energy: -1.5
max-cut objective: -4.0
solution: [1. 0. 1. 0.]
solution objective: 4.0

../_images/tutorials_06_examples_max_cut_and_tsp_16_1.png

Ejecutar en una computadora cuántica#

Ejecutamos la rutina de optimización usando un ciclo de retroalimentación con una computadora cuántica que usa funciones de prueba construidas con rotaciones Y de un solo qubit, \(U_\mathrm{simple}(\theta) = \prod_{i=1}^n Y(\theta_{i})\), y los pasos de entrelazamiento \(U_\mathrm{entrelazador}\).

[9]:

algorithm_globals.random_seed = 123
seed = 10598

[10]:

# construct SamplingVQE
optimizer = SPSA(maxiter=300)
ry = TwoLocal(qubitOp.num_qubits, "ry", "cz", reps=5, entanglement="linear")
vqe = SamplingVQE(sampler=Sampler(), ansatz=ry, optimizer=optimizer)

# run SamplingVQE
result = vqe.compute_minimum_eigenvalue(qubitOp)

# print results
x = max_cut.sample_most_likely(result.eigenstate)
print("energy:", result.eigenvalue.real)
print("time:", result.optimizer_time)
print("max-cut objective:", result.eigenvalue.real + offset)
print("solution:", x)
print("solution objective:", qp.objective.evaluate(x))

# plot results
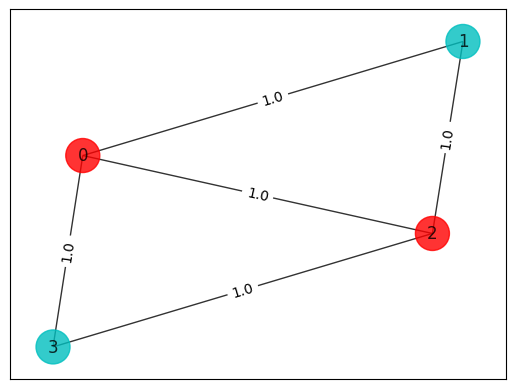
colors = ["r" if x[i] == 0 else "c" for i in range(n)]
draw_graph(G, colors, pos)

energy: -1.4996861455587311
time: 8.708028078079224
max-cut objective: -3.999686145558731
solution: [0 1 0 1]
solution objective: 4.0

../_images/tutorials_06_examples_max_cut_and_tsp_19_1.png

[11]:

# create minimum eigen optimizer based on SamplingVQE
vqe_optimizer = MinimumEigenOptimizer(vqe)

# solve quadratic program
result = vqe_optimizer.solve(qp)
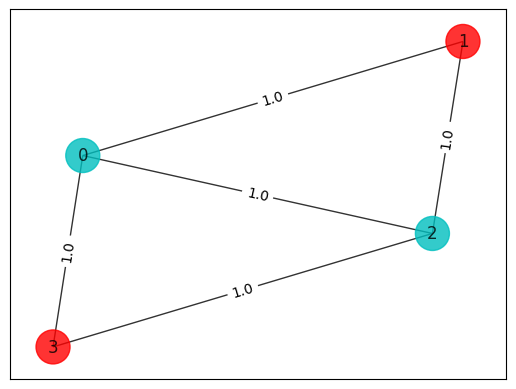
print(result.prettyprint())

colors = ["r" if result.x[i] == 0 else "c" for i in range(n)]
draw_graph(G, colors, pos)

objective function value: 4.0
variable values: x_0=1.0, x_1=0.0, x_2=1.0, x_3=0.0
status: SUCCESS

../_images/tutorials_06_examples_max_cut_and_tsp_20_1.png

Problema del Vendedor Viajero#

Además de ser notoriamente un problema NP completo que ha llamado la atención de científicos computacionales y matemáticos durante más de dos siglos, el Problema del Vendedor Viajero (Traveling Salesman Problem, TSP) tiene importantes repercusiones en las finanzas y la mercadotecnia, como su nombre lo indica. Coloquialmente hablando, el vendedor viajero es una persona que va de ciudad en ciudad para vender mercancía. El objetivo en este caso es encontrar el camino más corto que le permita al vendedor visitar todas las ciudades y regresar a su ciudad natal, es decir, la ciudad donde comenzó a viajar. Al hacer esto, el vendedor puede maximizar las ventas potenciales en la menor cantidad de tiempo.

El problema deriva su importancia de su «dureza» y equivalencia ubicua con otros problemas de optimización combinatoria relevantes que surgen en la práctica.

La formulación matemática con algunos análisis tempranos fue propuesta por W.R. Hamilton a principios del siglo XIX. Matemáticamente, el problema es, como en el caso de Max-Cut, mejor resumido en términos de grafos. El TSP en los nodos de un grafo busca el ciclo Hamiltoniano más corto que se puede tomar a través de cada uno de los nodos. Un ciclo de Hamilton es un camino cerrado que usa cada vértice de un grafo una vez. Se desconoce la solución general y no se espera que exista un algoritmo que la encuentre de manera eficiente (por ejemplo, en tiempo polinomial).

Encuentra el ciclo Hamiltoniano más corto en un grafo \(G=(V,E)\) con \(n=|V|\) nodos y distancias, \(w_{ij}\) (distancia desde el vértice \(i\) al vértice \(j\)). Un ciclo Hamiltoniano se describe mediante \(N^2\) variables \(x_{i,p}\), donde \(i\) representa el nodo y \(p\) representa su orden en una perspectiva de ciclo. La variable de decisión toma el valor 1 si la solución ocurre en el nodo \(i\) en el orden de tiempo \(p\). Requerimos que cada nodo solo pueda aparecer una vez en el ciclo, y por cada vez un nodo tiene que ocurrir. Esto equivale a las dos restricciones (aquí y a continuación, siempre que no se especifique, los sumandos se ejecutan sobre 0,1,…N-1)

\[\sum_{i} x_{i,p} = 1 ~~\forall p\]

\[\sum_{p} x_{i,p} = 1 ~~\forall i.\]

Para los nodos en nuestro ordenamiento prospectivo, si \(x_{i,p}\) y \(x_{j,p+1}\) son ambos 1, entonces debería haber una penalización de energía si \((i,j) \notin E\) (no conectado en el grafo). La forma de esta penalización es

\[\sum_{i,j\notin E}\sum_{p} x_{i,p}x_{j,p+1}>0,\]

donde se asume la condición de frontera de los ciclos Hamiltonianos \((p=N)\equiv (p=0)\). Sin embargo, aquí se supondrá un grafo completamente conectado y no incluirá este término. La distancia que se debe minimizar es

\[C(\textbf{x})=\sum_{i,j}w_{ij}\sum_{p} x_{i,p}x_{j,p+1}.\]

Poniendo todo esto junto en una única función objetivo para minimizar, obtenemos lo siguiente:

\[C(\textbf{x})=\sum_{i,j}w_{ij}\sum_{p} x_{i,p}x_{j,p+1}+ A\sum_p\left(1- \sum_i x_{i,p}\right)^2+A\sum_i\left(1- \sum_p x_{i,p}\right)^2,\]

donde \(A\) es un parámetro libre. Es necesario asegurarse de que \(A\) sea lo suficientemente grande como para que se respeten estas restricciones. Una forma de hacer esto es elegir \(A\) tal que \(A > \mathrm{max}(w_{ij})\).

Una vez más, es fácil mapear el problema de esta forma a una computadora cuántica, y la solución se encontrará minimizando un Hamiltoniano de Ising.

[12]:

# Generating a graph of 3 nodes
n = 3
num_qubits = n**2
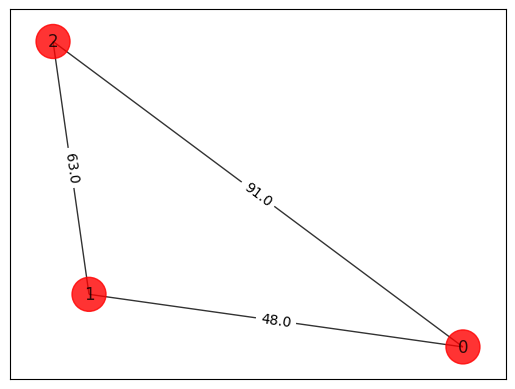
tsp = Tsp.create_random_instance(n, seed=123)
adj_matrix = nx.to_numpy_array(tsp.graph)
print("distance\n", adj_matrix)

colors = ["r" for node in tsp.graph.nodes]
pos = [tsp.graph.nodes[node]["pos"] for node in tsp.graph.nodes]
draw_graph(tsp.graph, colors, pos)

distance
 [[ 0. 48. 91.]
 [48.  0. 63.]
 [91. 63.  0.]]

../_images/tutorials_06_examples_max_cut_and_tsp_22_1.png

Enfoque de fuerza bruta#

[13]:

from itertools import permutations


def brute_force_tsp(w, N):
    a = list(permutations(range(1, N)))
    last_best_distance = 1e10
    for i in a:
        distance = 0
        pre_j = 0
        for j in i:
            distance = distance + w[j, pre_j]
            pre_j = j
        distance = distance + w[pre_j, 0]
        order = (0,) + i
        if distance < last_best_distance:
            best_order = order
            last_best_distance = distance
            print("order = " + str(order) + " Distance = " + str(distance))
    return last_best_distance, best_order


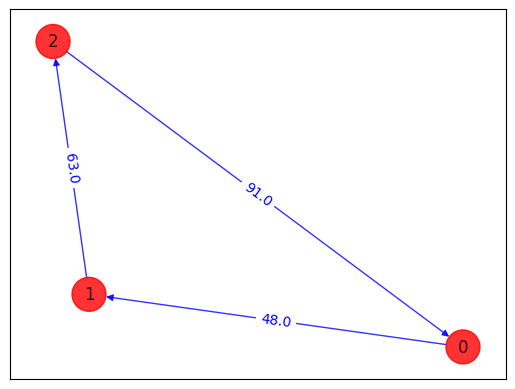
best_distance, best_order = brute_force_tsp(adj_matrix, n)
print(
    "Best order from brute force = "
    + str(best_order)
    + " with total distance = "
    + str(best_distance)
)


def draw_tsp_solution(G, order, colors, pos):
    G2 = nx.DiGraph()
    G2.add_nodes_from(G)
    n = len(order)
    for i in range(n):
        j = (i + 1) % n
        G2.add_edge(order[i], order[j], weight=G[order[i]][order[j]]["weight"])
    default_axes = plt.axes(frameon=True)
    nx.draw_networkx(
        G2, node_color=colors, edge_color="b", node_size=600, alpha=0.8, ax=default_axes, pos=pos
    )
    edge_labels = nx.get_edge_attributes(G2, "weight")
    nx.draw_networkx_edge_labels(G2, pos, font_color="b", edge_labels=edge_labels)


draw_tsp_solution(tsp.graph, best_order, colors, pos)

order = (0, 1, 2) Distance = 202.0
Best order from brute force = (0, 1, 2) with total distance = 202.0

../_images/tutorials_06_examples_max_cut_and_tsp_24_1.png

Mapear del problema de Ising#

[14]:

qp = tsp.to_quadratic_program()
print(qp.prettyprint())

Problem name: TSP

Minimize
  48*x_0_0*x_1_1 + 48*x_0_0*x_1_2 + 91*x_0_0*x_2_1 + 91*x_0_0*x_2_2
  + 48*x_0_1*x_1_0 + 48*x_0_1*x_1_2 + 91*x_0_1*x_2_0 + 91*x_0_1*x_2_2
  + 48*x_0_2*x_1_0 + 48*x_0_2*x_1_1 + 91*x_0_2*x_2_0 + 91*x_0_2*x_2_1
  + 63*x_1_0*x_2_1 + 63*x_1_0*x_2_2 + 63*x_1_1*x_2_0 + 63*x_1_1*x_2_2
  + 63*x_1_2*x_2_0 + 63*x_1_2*x_2_1

Subject to
  Linear constraints (6)
    x_0_0 + x_0_1 + x_0_2 == 1  'c0'
    x_1_0 + x_1_1 + x_1_2 == 1  'c1'
    x_2_0 + x_2_1 + x_2_2 == 1  'c2'
    x_0_0 + x_1_0 + x_2_0 == 1  'c3'
    x_0_1 + x_1_1 + x_2_1 == 1  'c4'
    x_0_2 + x_1_2 + x_2_2 == 1  'c5'

  Binary variables (9)
    x_0_0 x_0_1 x_0_2 x_1_0 x_1_1 x_1_2 x_2_0 x_2_1 x_2_2

[15]:

from qiskit_optimization.converters import QuadraticProgramToQubo

qp2qubo = QuadraticProgramToQubo()
qubo = qp2qubo.convert(qp)
qubitOp, offset = qubo.to_ising()
print("Offset:", offset)
print("Ising Hamiltonian:")
print(str(qubitOp))

Offset: 7581.0
Ising Hamiltonian:
SparsePauliOp(['IIIIIIIIZ', 'IIIIIIIZI', 'IIIIIIZII', 'IIIIIZIII', 'IIIIZIIII', 'IIIZIIIII', 'IIZIIIIII', 'IZIIIIIII', 'ZIIIIIIII', 'IIIIIIIZZ', 'IIIIIIZIZ', 'IIIIIIZZI', 'IIIIIZIIZ', 'IIIIIZIZI', 'IIIIIZZII', 'IIIIZIIIZ', 'IIIIZIIZI', 'IIIIZIZII', 'IIIIZZIII', 'IIIZIIIIZ', 'IIIZIIIZI', 'IIIZIIZII', 'IIIZIZIII', 'IIIZZIIII', 'IIZIIIIIZ', 'IIZIIIIZI', 'IIZIIIZII', 'IIZIIZIII', 'IIZIZIIII', 'IIZZIIIII', 'IZIIIIIIZ', 'IZIIIIIZI', 'IZIIIIZII', 'IZIIIZIII', 'IZIIZIIII', 'IZIZIIIII', 'IZZIIIIII', 'ZIIIIIIIZ', 'ZIIIIIIZI', 'ZIIIIIZII', 'ZIIIIZIII', 'ZIIIZIIII', 'ZIIZIIIII', 'ZIZIIIIII', 'ZZIIIIIII'],
              coeffs=[-1282.5 +0.j, -1282.5 +0.j, -1282.5 +0.j, -1268.5 +0.j, -1268.5 +0.j,
 -1268.5 +0.j, -1290.  +0.j, -1290.  +0.j, -1290.  +0.j,   606.5 +0.j,
   606.5 +0.j,   606.5 +0.j,   606.5 +0.j,    12.  +0.j,    12.  +0.j,
    12.  +0.j,   606.5 +0.j,    12.  +0.j,   606.5 +0.j,    12.  +0.j,
    12.  +0.j,   606.5 +0.j,   606.5 +0.j,   606.5 +0.j,   606.5 +0.j,
    22.75+0.j,    22.75+0.j,   606.5 +0.j,    15.75+0.j,    15.75+0.j,
    22.75+0.j,   606.5 +0.j,    22.75+0.j,    15.75+0.j,   606.5 +0.j,
    15.75+0.j,   606.5 +0.j,    22.75+0.j,    22.75+0.j,   606.5 +0.j,
    15.75+0.j,    15.75+0.j,   606.5 +0.j,   606.5 +0.j,   606.5 +0.j])

[16]:

result = exact.solve(qubo)
print(result.prettyprint())

objective function value: 202.0
variable values: x_0_0=1.0, x_0_1=0.0, x_0_2=0.0, x_1_0=0.0, x_1_1=1.0, x_1_2=0.0, x_2_0=0.0, x_2_1=0.0, x_2_2=1.0
status: SUCCESS

Verificar que el Hamiltoniano completo proporcione el costo correcto#

[17]:

# Making the Hamiltonian in its full form and getting the lowest eigenvalue and eigenvector
ee = NumPyMinimumEigensolver()
result = ee.compute_minimum_eigenvalue(qubitOp)

print("energy:", result.eigenvalue.real)
print("tsp objective:", result.eigenvalue.real + offset)
x = tsp.sample_most_likely(result.eigenstate)
print("feasible:", qubo.is_feasible(x))
z = tsp.interpret(x)
print("solution:", z)
print("solution objective:", tsp.tsp_value(z, adj_matrix))
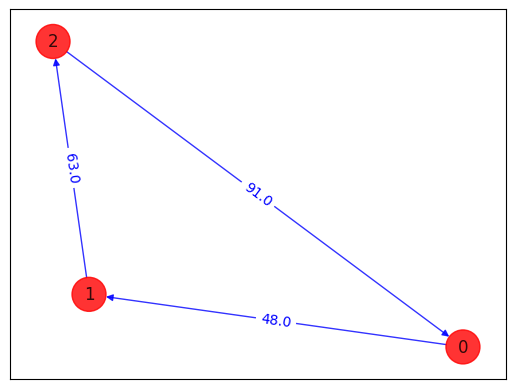
draw_tsp_solution(tsp.graph, z, colors, pos)

energy: -7379.0
tsp objective: 202.0
feasible: True
solution: [0, 1, 2]
solution objective: 202.0

../_images/tutorials_06_examples_max_cut_and_tsp_30_1.png

Ejecutar en una computadora cuántica#

[18]:

algorithm_globals.random_seed = 123
seed = 10598

[19]:

optimizer = SPSA(maxiter=300)
ry = TwoLocal(qubitOp.num_qubits, "ry", "cz", reps=5, entanglement="linear")
vqe = SamplingVQE(sampler=Sampler(), ansatz=ry, optimizer=optimizer)

result = vqe.compute_minimum_eigenvalue(qubitOp)

print("energy:", result.eigenvalue.real)
print("time:", result.optimizer_time)
x = tsp.sample_most_likely(result.eigenstate)
print("feasible:", qubo.is_feasible(x))
z = tsp.interpret(x)
print("solution:", z)
print("solution objective:", tsp.tsp_value(z, adj_matrix))
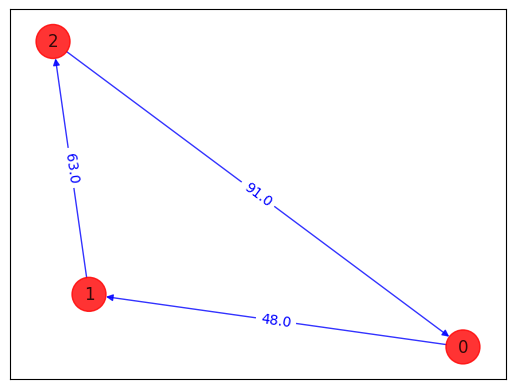
draw_tsp_solution(tsp.graph, z, colors, pos)

energy: -7326.024699521861
time: 28.526036977767944
feasible: True
solution: [1, 2, 0]
solution objective: 202.0

../_images/tutorials_06_examples_max_cut_and_tsp_33_1.png

[20]:

algorithm_globals.random_seed = 123
seed = 10598

[21]:

# create minimum eigen optimizer based on SamplingVQE
vqe_optimizer = MinimumEigenOptimizer(vqe)

# solve quadratic program
result = vqe_optimizer.solve(qp)
print(result.prettyprint())

z = tsp.interpret(x)
print("solution:", z)
print("solution objective:", tsp.tsp_value(z, adj_matrix))
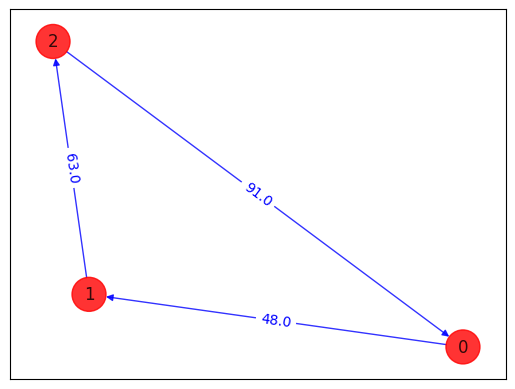
draw_tsp_solution(tsp.graph, z, colors, pos)

objective function value: 202.0
variable values: x_0_0=0.0, x_0_1=0.0, x_0_2=1.0, x_1_0=1.0, x_1_1=0.0, x_1_2=0.0, x_2_0=0.0, x_2_1=1.0, x_2_2=0.0
status: SUCCESS
solution: [1, 2, 0]
solution objective: 202.0

../_images/tutorials_06_examples_max_cut_and_tsp_35_1.png

[22]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
`qiskit-terra`	0.25.0.dev0+1d844ec
`qiskit-aer`	0.12.0
`qiskit-ibmq-provider`	0.20.2
`qiskit-nature`	0.7.0
`qiskit-optimization`	0.6.0
System information
Python version	3.10.11
Python compiler	Clang 14.0.0 (clang-1400.0.29.202)
Python build	main, Apr 7 2023 07:31:31
OS	Darwin
CPUs	4
Memory (Gb)	16.0
Thu May 18 16:57:58 2023 JST

This code is a part of Qiskit

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.

[ ]: