Nota

Esta página fue generada a partir de docs/tutorials/10_warm_start_qaoa.ipynb.

Optimización cuántica de arranque en caliente (warm-starting)#

Introducción#

Los problemas de optimización con variables enteras o restricciones a menudo son difíciles de resolver. Por ejemplo, el problema de Optimización Binaria Cuadrática Sin Restricciones (Quadratic Unconstrained Binary Optimization, QUBO), es decir,

\begin{align} \min_{x\in\{0,1\}^n}x^T\Sigma x + \mu^Tx, \end{align}

es NP difícil. Aquí, \(\Sigma\) es una matriz \(n\times n\) y \(x\) es un vector de \(n\) variables binarias. Ten en cuenta que podríamos haber agregado el término lineal \(\mu\) a la diagonal como \(x_i^2=x_i\) para \(x_i\in\{0, 1\}\). Si bien los QUBO son difíciles de resolver, existen muchas formas de relajarlos a problemas que son más fáciles de resolver. Por ejemplo, si \(\Sigma\) es semi-definido positivo, el QUBO se puede relajar y da como resultado un Programa Cuadrático convexo

\begin{align} \min_{x\in[0,1]^n}x^T\Sigma x, \end{align}

que se vuelve fácil de resolver como \(x\) ahora representa \(n\) variables continuas restringidas al rango \([0, 1]\). Estas relajaciones pueden aprovecharse para arrancar en caliente (warm-start) algoritmos de optimización cuántica como se muestra en [1].

Referencias#

[1] D. J. Egger, J Marecek, S. Woerner, Warm-starting quantum optimization, arXiv:2009.10095

[1]:

import numpy as np
import copy

# Problem modelling imports
from docplex.mp.model import Model

# Qiskit imports
from qiskit_algorithms import QAOA, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import COBYLA
from qiskit_algorithms.utils.algorithm_globals import algorithm_globals
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import MinimumEigenOptimizer, CplexOptimizer
from qiskit_optimization import QuadraticProgram
from qiskit_optimization.problems.variable import VarType
from qiskit_optimization.converters.quadratic_program_to_qubo import QuadraticProgramToQubo
from qiskit_optimization.translators import from_docplex_mp

Preliminares: relajando QUBOs#

Primero, mostramos cómo relajar un QUBO construido con una matriz semi-definida positiva para obtener un QP fácil de resolver.

[2]:

def create_problem(mu: np.array, sigma: np.array, total: int = 3) -> QuadraticProgram:
    """Solve the quadratic program using docplex."""

    mdl = Model()
    x = [mdl.binary_var("x%s" % i) for i in range(len(sigma))]

    objective = mdl.sum([mu[i] * x[i] for i in range(len(mu))])
    objective -= 2 * mdl.sum(
        [sigma[i, j] * x[i] * x[j] for i in range(len(mu)) for j in range(len(mu))]
    )
    mdl.maximize(objective)
    cost = mdl.sum(x)
    mdl.add_constraint(cost == total)

    qp = from_docplex_mp(mdl)
    return qp


def relax_problem(problem) -> QuadraticProgram:
    """Change all variables to continuous."""
    relaxed_problem = copy.deepcopy(problem)
    for variable in relaxed_problem.variables:
        variable.vartype = VarType.CONTINUOUS

    return relaxed_problem

Para este ejemplo, usamos una matriz semi-definida positiva \(\Sigma\) y un término lineal \(\mu\) como se define a continuación.

[3]:

mu = np.array([3.418, 2.0913, 6.2415, 4.4436, 10.892, 3.4051])
sigma = np.array(
    [
        [1.07978412, 0.00768914, 0.11227606, -0.06842969, -0.01016793, -0.00839765],
        [0.00768914, 0.10922887, -0.03043424, -0.0020045, 0.00670929, 0.0147937],
        [0.11227606, -0.03043424, 0.985353, 0.02307313, -0.05249785, 0.00904119],
        [-0.06842969, -0.0020045, 0.02307313, 0.6043817, 0.03740115, -0.00945322],
        [-0.01016793, 0.00670929, -0.05249785, 0.03740115, 0.79839634, 0.07616951],
        [-0.00839765, 0.0147937, 0.00904119, -0.00945322, 0.07616951, 1.08464544],
    ]
)

Utilizando DOCPLEX construimos un modelo con variables binarias.

[4]:

qubo = create_problem(mu, sigma)
print(qubo.prettyprint())

Problem name: docplex_model1

Maximize
  -2.15956824*x0^2 - 0.03075656*x0*x1 - 0.44910424*x0*x2 + 0.27371876*x0*x3
  + 0.04067172*x0*x4 + 0.0335906*x0*x5 - 0.21845774*x1^2 + 0.12173696*x1*x2
  + 0.008018*x1*x3 - 0.02683716*x1*x4 - 0.0591748*x1*x5 - 1.970706*x2^2
  - 0.09229252*x2*x3 + 0.2099914*x2*x4 - 0.03616476*x2*x5 - 1.2087634*x3^2
  - 0.1496046*x3*x4 + 0.03781288*x3*x5 - 1.59679268*x4^2 - 0.30467804*x4*x5
  - 2.16929088*x5^2 + 3.418*x0 + 2.0913*x1 + 6.2415*x2 + 4.4436*x3 + 10.892*x4
  + 3.4051*x5

Subject to
  Linear constraints (1)
    x0 + x1 + x2 + x3 + x4 + x5 == 3  'c0'

  Binary variables (6)
    x0 x1 x2 x3 x4 x5

Tales problemas binarios son difíciles de tratar, pero se pueden resolver si la instancia del problema es lo suficientemente pequeña. Nuestro ejemplo anterior tiene como solución

[5]:

result = CplexOptimizer().solve(qubo)
print(result.prettyprint())

objective function value: 16.7689322
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS

Podemos crear una relajación de este problema en el que las variables ya no son binarias. Ten en cuenta que usamos el convertidor QuadraticProgramToQubo para transformar la restricción en un término de penalización cuadrático. Hacemos esto para mantener la coherencia con los pasos que aplica internamente el módulo de optimización de Qiskit.

[6]:

qp = relax_problem(QuadraticProgramToQubo().convert(qubo))
print(qp.prettyprint())

Problem name: docplex_model1

Minimize
  44.84880018*x0^2 + 85.40922044*x0*x1 + 85.82756812*x0*x2
  + 85.10474511999999*x0*x3 + 85.33779215999999*x0*x4 + 85.34487328*x0*x5
  + 42.90768968*x1^2 + 85.25672692*x1*x2 + 85.37044588*x1*x3 + 85.40530104*x1*x4
  + 85.43763867999999*x1*x5 + 44.65993794*x2^2 + 85.4707564*x2*x3
  + 85.16847247999999*x2*x4 + 85.41462863999999*x2*x5 + 43.89799534*x3^2
  + 85.52806848*x3*x4 + 85.34065100000001*x3*x5 + 44.28602462*x4^2
  + 85.68314192*x4*x5 + 44.85852282*x5^2 - 259.55339164*x0
  - 258.22669163999996*x1 - 262.37689163999994*x2 - 260.57899163999997*x3
  - 267.02739163999996*x4 - 259.54049163999997*x5 + 384.20308746

Subject to
  No constraints

  Continuous variables (6)
    0 <= x0 <= 1
    0 <= x1 <= 1
    0 <= x2 <= 1
    0 <= x3 <= 1
    0 <= x4 <= 1
    0 <= x5 <= 1

La solución de esta relajación continua es diferente de la solución del problema binario, pero se puede utilizar para iniciar en caliente (warm-start) un solucionador cuando se trata de un problema binario.

[7]:

sol = CplexOptimizer().solve(qp)
print(sol.prettyprint())

objective function value: -17.01205502568274
variable values: x0=0.17524995761801201, x1=1.4803888163984595e-07, x2=0.9709053264087679, x3=0.7384168677494151, x4=0.9999999916475085, x5=0.14438904470168346
status: SUCCESS

[8]:

c_stars = sol.samples[0].x
print(c_stars)

[0.17524995761801201, 1.4803888163984595e-07, 0.9709053264087679, 0.7384168677494151, 0.9999999916475085, 0.14438904470168346]

QAOA#

Aquí, ilustramos cómo arrancar en caliente (warm-start) el algoritmo cuántico de optimización aproximada (quantum approximate optimization algorithm, QAOA) aprovechando el problema relajado que se muestra arriba.

QAOA estándar#

Primero, usamos QAOA estándar para resolver el QUBO. Para hacer esto, convertimos QUBO a la clase QuadraticProgram (ten en cuenta que el problema resultante sigue siendo un problema binario).

[9]:

algorithm_globals.random_seed = 12345
qaoa_mes = QAOA(sampler=Sampler(), optimizer=COBYLA(), initial_point=[0.0, 1.0])
exact_mes = NumPyMinimumEigensolver()

[10]:

qaoa = MinimumEigenOptimizer(qaoa_mes)

[11]:

qaoa_result = qaoa.solve(qubo)
print(qaoa_result.prettyprint())

objective function value: 16.768932200000002
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS

QAOA de arranque en caliente (warm-start)#

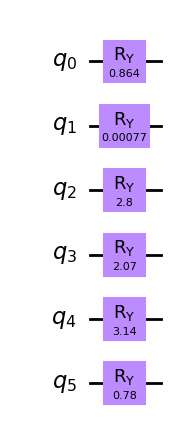
A continuación, comparamos este resultado con un QAOA de arranque en caliente (warm-start) en el que usamos la solución para la relajación continua del problema. Primero, creamos el estado inicial

\begin{align} |\phi^*\rangle=\bigotimes_{i=0}^{n-1}R_y(\theta_i)|0\rangle_n . \end{align}

que se obtiene aplicando rotaciones \(R_y\) con un ángulo \(\theta=2\arcsin(\sqrt{c^*_i})\) que depende de la solución al problema relajado. Aquí, \(c^*_i\) es el valor de la variable \(i\) del problema relajado.

[26]:

from qiskit import QuantumCircuit

thetas = [2 * np.arcsin(np.sqrt(c_star)) for c_star in c_stars]

init_qc = QuantumCircuit(len(sigma))
for idx, theta in enumerate(thetas):
    init_qc.ry(theta, idx)

init_qc.draw(output="mpl", style="clifford")

[26]:

../_images/tutorials_10_warm_start_qaoa_20_0.png

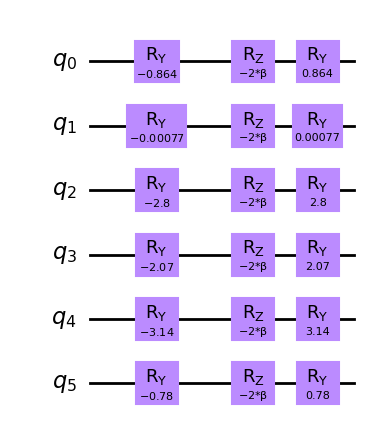
Después, creamos el operador mezclador para QAOA. Al arrancar QAOA en caliente (warm-starting), debemos asegurarnos de que el operador del mezclador tenga el estado inicial como estado fundamental. Por lo tanto, elegimos el Hamiltoniano

\begin{align} H_{M,i}^{(ws)}= \begin{pmatrix} 2c_i^*-1 & -2\sqrt{c_i^*(1-c_i^*)} \\ -2\sqrt{c_i^*(1-c_i^*)} & 1-2c_i^* \end{pmatrix} \end{align}

como operador mezclador para el qubit \(i\). Una vez multiplicado por \(-i\beta\) y exponenciado, este mezclador produce el siguiente circuito mezclador.

[27]:

from qiskit.circuit import Parameter

beta = Parameter("β")

ws_mixer = QuantumCircuit(len(sigma))
for idx, theta in enumerate(thetas):
    ws_mixer.ry(-theta, idx)
    ws_mixer.rz(-2 * beta, idx)
    ws_mixer.ry(theta, idx)

ws_mixer.draw(output="mpl", style="clifford")

[27]:

../_images/tutorials_10_warm_start_qaoa_22_0.png

El estado inicial y el operador mezclador se pueden pasar a QAOA.

[14]:

ws_qaoa_mes = QAOA(
    sampler=Sampler(),
    optimizer=COBYLA(),
    initial_state=init_qc,
    mixer=ws_mixer,
    initial_point=[0.0, 1.0],
)

[15]:

ws_qaoa = MinimumEigenOptimizer(ws_qaoa_mes)

[16]:

ws_qaoa_result = ws_qaoa.solve(qubo)
print(ws_qaoa_result.prettyprint())

objective function value: 16.768932200000002
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS

Análisis#

Ambos resultados parecen dar el mismo resultado. Sin embargo, cuando observamos la distribución subyacente de probabilidades observamos que el arranque en caliente (warm-start) de QAOA tiene una probabilidad mucho mayor de muestrear la solución óptima.

[17]:

def format_qaoa_samples(samples, max_len: int = 10):
    qaoa_res = []
    for s in samples:
        if sum(s.x) == 3:
            qaoa_res.append(("".join([str(int(_)) for _ in s.x]), s.fval, s.probability))

    res = sorted(qaoa_res, key=lambda x: -x[1])[0:max_len]

    return [(_[0] + f": value: {_[1]:.3f}, probability: {1e2*_[2]:.1f}%") for _ in res]


format_qaoa_samples(qaoa_result.samples)

[17]:

['001110: value: 16.769, probability: 0.7%',
 '011010: value: 15.744, probability: 0.7%',
 '001011: value: 14.671, probability: 0.6%',
 '101010: value: 14.626, probability: 0.7%',
 '010110: value: 14.234, probability: 2.3%',
 '100110: value: 13.953, probability: 1.6%',
 '000111: value: 13.349, probability: 1.5%',
 '110010: value: 12.410, probability: 3.0%',
 '010011: value: 12.013, probability: 2.7%',
 '100011: value: 11.559, probability: 3.3%']

[18]:

format_qaoa_samples(ws_qaoa_result.samples)

[18]:

['001110: value: 16.769, probability: 72.8%',
 '001011: value: 14.671, probability: 1.2%',
 '101010: value: 14.626, probability: 2.6%',
 '100110: value: 13.953, probability: 0.3%',
 '000111: value: 13.349, probability: 0.1%',
 '100011: value: 11.559, probability: 0.0%']

QAOA de arranque en caliente (warm-start)#

Las características del inicio en caliente (warm-start) anteriores están disponibles en el módulo de optimización de Qiskit como un optimizador único llamado WarmStartQAOAOptimizer que se ilustra a continuación. Este solucionador resolverá un QUBO con un QAOA de arranque en caliente (warm-start). Calcula \(c^*\) relajando el problema. Este comportamiento se controla configurando relax_for_pre_solver en True.

[19]:

from qiskit_optimization.algorithms import WarmStartQAOAOptimizer

[20]:

qaoa_mes = QAOA(sampler=Sampler(), optimizer=COBYLA(), initial_point=[0.0, 1.0])
ws_qaoa = WarmStartQAOAOptimizer(
    pre_solver=CplexOptimizer(), relax_for_pre_solver=True, qaoa=qaoa_mes, epsilon=0.0
)

[21]:

ws_result = ws_qaoa.solve(qubo)
print(ws_result.prettyprint())

objective function value: 16.768932200000002
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS

[22]:

format_qaoa_samples(ws_result.samples)

[22]:

['001110: value: 16.769, probability: 72.8%',
 '001011: value: 14.671, probability: 1.2%',
 '101010: value: 14.626, probability: 2.6%',
 '100110: value: 13.953, probability: 0.3%',
 '000111: value: 13.349, probability: 0.1%',
 '100011: value: 11.559, probability: 0.0%']

[23]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Software	Version
`qiskit`	0.45.1
`qiskit_algorithms`	0.2.1
`qiskit_optimization`	0.7.0
System information
Python version	3.10.13
Python compiler	GCC 13.2.1 20230728 (Red Hat 13.2.1-1)
Python build	main, Aug 28 2023 00:00:00
OS	Linux
CPUs	12
Memory (Gb)	31.056411743164062
Wed Dec 06 10:26:59 2023 CET

This code is a part of Qiskit

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.

[ ]: