নোট
এই পৃষ্ঠাটি docs/tutorials/10_warm_start_qaoa.ipynb -থেকে বানানো হয়েছে।
কোয়ান্টাম অনুকূলকরণের (অপটিমাইজেশন) প্রস্তুতিপর্ব#
ভূমিকা#
পূর্ণসংখ্যা জাতীয় চলরাশি বা শর্তবিশিষ্ট অনুকূলায়ন (অপ্টিমাইজেশন) সমস্যাসমূহর সমাধান করা সাধারণত জটিল হয়। উদাহরণস্বরূপ, শর্তহীন দ্বিঘাত দ্বিমিক অনুকূলায়ন (অপ্টিমাইজেশন) (কিউইউবিও (QUBO)) সমস্যা, অর্থাৎ
\begin{align} \min_{x\in\{0,1\}^n}x^T\Sigma x + \mu^Tx, \end{align}
হলো এনপি-হার্ড। এখানে \(\Sigma\) হলো একটি \(n\ গুণ n\) ম্যাট্রিক্স এবং \(x\) হলো \(n\) দ্বিমিক (বাইনারি) চলরাশির দিকরাশি। মনে রেখো আমরা কর্ণে রৈখিক পদ \(\mu\) যোগ করতে পারতাম, কারণ \(x_i^2=x_i\) যখন \(x_i\in\{0, 1\}\)। কিউইউবিও (QUBO) সমাধান করা কঠিন হলেও আমরা বিভিন্ন পদ্ধতিতে এগুলোকে শিথিল করে সমাধানযোগ্য করতে পারি। উদাহরণস্বরূপ, যদি \(\Sigma\) একটা অর্ধ-নিশ্চিত ধনাত্মক তাহলে কিউইউবিও (QUBO) -কে শিথিল করে একটা উত্তল দ্বিঘাত (কোয়াড্রাটিক) নির্দেশমালাতে পরিবর্তন করা যায়
\begin{align} \min_{x\in[0,1]^n}x^T\Sigma x, \end{align}
যেটার সমাধান তুলনামূলকভাবে সহজ কারণ \(x\) এখন \(n\) গুলো \([0, 1]\) সীমার মধ্যে সীমিত অবিচ্ছিন্ন চলরাশির প্রতিনিধিত্ব করে। এরকম শিথিলকরণ (রিলাক্সেশন) এর উপর নির্ভর করে কোয়ান্টাম অনুকূলকরণ (অপটিমাইজেশন) অ্যালোগরিদমের প্রস্তুতি নেওয়া যেতে পারে (চিত্র [১])।
তথ্যসূত্র#
[১] D. J. Egger, J Marecek, S. Woerner, Warm-starting quantum optimization, arXiv:2009.10095
[1]:
import numpy as np
import copy
# Problem modelling imports
from docplex.mp.model import Model
# Qiskit imports
from qiskit_algorithms import QAOA, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import COBYLA
from qiskit_algorithms.utils.algorithm_globals import algorithm_globals
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import MinimumEigenOptimizer, CplexOptimizer
from qiskit_optimization import QuadraticProgram
from qiskit_optimization.problems.variable import VarType
from qiskit_optimization.converters.quadratic_program_to_qubo import QuadraticProgramToQubo
from qiskit_optimization.translators import from_docplex_mp
প্রাথমিক: কিউইউবিও (QUBO) এর শিথিলকরণ#
প্রথমে আমরা দেখবো কিভাবে একটা অর্ধ-নিশ্চিত ধনাত্মক ম্যাট্রিক্স দ্বারা বানানো কিউইউবিও (QUBO) এর শিথিলকরন করে একটা সহজ কিউপি বানানো যায়।
[2]:
def create_problem(mu: np.array, sigma: np.array, total: int = 3) -> QuadraticProgram:
"""Solve the quadratic program using docplex."""
mdl = Model()
x = [mdl.binary_var("x%s" % i) for i in range(len(sigma))]
objective = mdl.sum([mu[i] * x[i] for i in range(len(mu))])
objective -= 2 * mdl.sum(
[sigma[i, j] * x[i] * x[j] for i in range(len(mu)) for j in range(len(mu))]
)
mdl.maximize(objective)
cost = mdl.sum(x)
mdl.add_constraint(cost == total)
qp = from_docplex_mp(mdl)
return qp
def relax_problem(problem) -> QuadraticProgram:
"""Change all variables to continuous."""
relaxed_problem = copy.deepcopy(problem)
for variable in relaxed_problem.variables:
variable.vartype = VarType.CONTINUOUS
return relaxed_problem
এই উদাহরণে আমরা নিম্নলিখিত একটা ধনাত্মক অর্ধনিশ্চিত ম্যাট্রিক্স \(\Sigma\) এবং একটা রৈখিক পদ \(\mu\) ব্যবহার করব।
[3]:
mu = np.array([3.418, 2.0913, 6.2415, 4.4436, 10.892, 3.4051])
sigma = np.array(
[
[1.07978412, 0.00768914, 0.11227606, -0.06842969, -0.01016793, -0.00839765],
[0.00768914, 0.10922887, -0.03043424, -0.0020045, 0.00670929, 0.0147937],
[0.11227606, -0.03043424, 0.985353, 0.02307313, -0.05249785, 0.00904119],
[-0.06842969, -0.0020045, 0.02307313, 0.6043817, 0.03740115, -0.00945322],
[-0.01016793, 0.00670929, -0.05249785, 0.03740115, 0.79839634, 0.07616951],
[-0.00839765, 0.0147937, 0.00904119, -0.00945322, 0.07616951, 1.08464544],
]
)
ডকপ্লেক্স ব্যবহার করে আমরা দ্বিমিক (বাইনারি) চলরাশিবিশিষ্ট একটা মডেল বানাবো।
[4]:
qubo = create_problem(mu, sigma)
print(qubo.prettyprint())
Problem name: docplex_model1
Maximize
-2.15956824*x0^2 - 0.03075656*x0*x1 - 0.44910424*x0*x2 + 0.27371876*x0*x3
+ 0.04067172*x0*x4 + 0.0335906*x0*x5 - 0.21845774*x1^2 + 0.12173696*x1*x2
+ 0.008018*x1*x3 - 0.02683716*x1*x4 - 0.0591748*x1*x5 - 1.970706*x2^2
- 0.09229252*x2*x3 + 0.2099914*x2*x4 - 0.03616476*x2*x5 - 1.2087634*x3^2
- 0.1496046*x3*x4 + 0.03781288*x3*x5 - 1.59679268*x4^2 - 0.30467804*x4*x5
- 2.16929088*x5^2 + 3.418*x0 + 2.0913*x1 + 6.2415*x2 + 4.4436*x3 + 10.892*x4
+ 3.4051*x5
Subject to
Linear constraints (1)
x0 + x1 + x2 + x3 + x4 + x5 == 3 'c0'
Binary variables (6)
x0 x1 x2 x3 x4 x5
এমন দ্বিমিক (বাইনারি) সমস্যা সমাধান করা কঠিন, কিন্তু সমস্যার দৃষ্টান্ত (ইনস্ট্যান্স) ছোট হলে সমাধান সম্ভব। উপরের উদাহরণের সমাধান আছে
[5]:
result = CplexOptimizer().solve(qubo)
print(result.prettyprint())
objective function value: 16.7689322
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS
আমরা এই সমস্যার একটি শিথিলতা তৈরি করতে পারি যেখানে ভেরিয়েবল আর বাইনারি নয়। মনে রাখবেন যে আমরা QuadraticProgramToQubo কনভার্টার ব্যবহার করে সীমাবদ্ধতাকে দ্বিঘাত পেনাল্টি টার্মে রূপান্তর করি। Qiskit অপ্টিমাইজেশন মডিউলটি অভ্যন্তরীণভাবে প্রযোজ্য ধাপগুলির সাথে সামঞ্জস্যপূর্ণ থাকার জন্য আমরা এটি করি।
[6]:
qp = relax_problem(QuadraticProgramToQubo().convert(qubo))
print(qp.prettyprint())
Problem name: docplex_model1
Minimize
44.84880018*x0^2 + 85.40922044*x0*x1 + 85.82756812*x0*x2
+ 85.10474511999999*x0*x3 + 85.33779215999999*x0*x4 + 85.34487328*x0*x5
+ 42.90768968*x1^2 + 85.25672692*x1*x2 + 85.37044588*x1*x3 + 85.40530104*x1*x4
+ 85.43763867999999*x1*x5 + 44.65993794*x2^2 + 85.4707564*x2*x3
+ 85.16847247999999*x2*x4 + 85.41462863999999*x2*x5 + 43.89799534*x3^2
+ 85.52806848*x3*x4 + 85.34065100000001*x3*x5 + 44.28602462*x4^2
+ 85.68314192*x4*x5 + 44.85852282*x5^2 - 259.55339164*x0
- 258.22669163999996*x1 - 262.37689163999994*x2 - 260.57899163999997*x3
- 267.02739163999996*x4 - 259.54049163999997*x5 + 384.20308746
Subject to
No constraints
Continuous variables (6)
0 <= x0 <= 1
0 <= x1 <= 1
0 <= x2 <= 1
0 <= x3 <= 1
0 <= x4 <= 1
0 <= x5 <= 1
এই ক্রমাগত শিথিলকরণ (রিলাক্সেশন) সমাধান বাইনারি সমস্যার সমাধান থেকে আলাদা কিন্তু বাইনারি সমস্যা মোকাবেলার সময় সমাধানকারীকে উষ্ণ-শুরু করতে ব্যবহার করা যেতে পারে।
[7]:
sol = CplexOptimizer().solve(qp)
print(sol.prettyprint())
objective function value: -17.01205502568274
variable values: x0=0.17524995761801201, x1=1.4803888163984595e-07, x2=0.9709053264087679, x3=0.7384168677494151, x4=0.9999999916475085, x5=0.14438904470168346
status: SUCCESS
[8]:
c_stars = sol.samples[0].x
print(c_stars)
[0.17524995761801201, 1.4803888163984595e-07, 0.9709053264087679, 0.7384168677494151, 0.9999999916475085, 0.14438904470168346]
কিউএওএ (QAOA)#
এখানে, আমরা দেখিয়েছি কিভাবে উপরে দেখানো শিথিলকরণ সমস্যাটি ব্যবহার করে কোয়ান্টাম অ্যাপ্রক্সিমেইট অপ্টিমাইজেশন অ্যালগরিদম (QAOA) উষ্ণ-শুরু করতে হয়।
সাধারণ কিউএওএ (QAOA)#
First, we use standard QAOA to solve the QUBO. To do this, we convert the QUBO to QuadraticProgram class (note that the resulting problem is still a binary problem).
[9]:
algorithm_globals.random_seed = 12345
qaoa_mes = QAOA(sampler=Sampler(), optimizer=COBYLA(), initial_point=[0.0, 1.0])
exact_mes = NumPyMinimumEigensolver()
[10]:
qaoa = MinimumEigenOptimizer(qaoa_mes)
[11]:
qaoa_result = qaoa.solve(qubo)
print(qaoa_result.prettyprint())
objective function value: 16.768932200000002
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS
কিউএওএ (QAOA) এর প্রস্তুতি#
পরবর্তী, আমরা এই ফলাফলটিকে একটি উষ্ণ-শুরু QAOA এর সাথে তুলনা করি যেখানে আমরা সমস্যার অবিরাম শিথিলতার সমাধান ব্যবহার করি। প্রথমত, আমরা প্রাথমিক মান বা অবস্থা তৈরি করি
\begin{align} |\phi^*\rangle=\bigotimes_{i=0}^{n-1}R_y(\theta_i)|0\rangle_n . \end{align}
যা \(\theta=2\arcsin(\sqrt{c^*_i})\) কোণ দিয়ে \(R_y\) ঘূর্ণন প্রয়োগ করে দেওয়া হয় যা আরামদায়ক সমস্যার সমাধানের উপর নির্ভর করে। এখানে, \(c^*_i\) হল আরামদায়ক সমস্যার পরিবর্তনশীল y এর মান।
[26]:
from qiskit import QuantumCircuit
thetas = [2 * np.arcsin(np.sqrt(c_star)) for c_star in c_stars]
init_qc = QuantumCircuit(len(sigma))
for idx, theta in enumerate(thetas):
init_qc.ry(theta, idx)
init_qc.draw(output="mpl", style="clifford")
[26]:
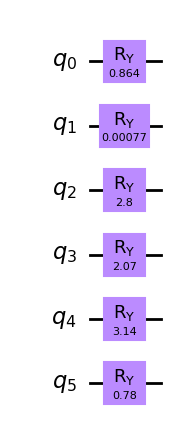
পরবর্তী, আমরা QAOA এর জন্য মিক্সার অপারেটর তৈরি করি। QAOA শুরু করার সময় আমাদের অবশ্যই নিশ্চিত করতে হবে যে মিক্সার অপারেটরের প্রাথমিক অবস্থা গ্রাউন্ড স্টেট হিসাবে আছে। তাই আমরা হ্যামিল্টোনিয়ানকে বেছে নিয়েছি
\begin{align} H_{M,i}^{(ws)}= \begin{pmatrix} 2c_i^*-1 & -2\sqrt{c_i^*(1-c_i^*)} \\ -2\sqrt{c_i^*(1-c_i^*)} & 1-2c_i^* \end{pmatrix} \end{align}
কিউবিট \(i\) এর জন্য মিক্সার অপারেটর হিসাবে। একবার \(-i\beta\) দ্বারা গুণিত এবং এক্সপোনেন্টিয়েটেড এই মিক্সার নিম্নলিখিত মিক্সার সার্কিট তৈরি করে।
[27]:
from qiskit.circuit import Parameter
beta = Parameter("β")
ws_mixer = QuantumCircuit(len(sigma))
for idx, theta in enumerate(thetas):
ws_mixer.ry(-theta, idx)
ws_mixer.rz(-2 * beta, idx)
ws_mixer.ry(theta, idx)
ws_mixer.draw(output="mpl", style="clifford")
[27]:
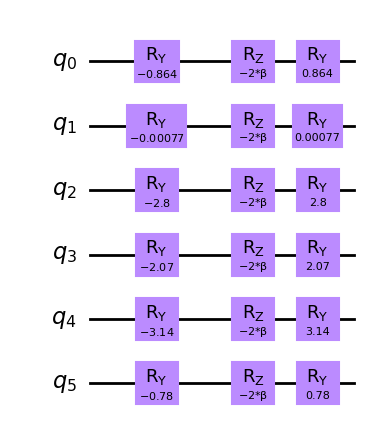
প্রাথমিক অবস্থা এবং মিক্সার অপারেটর তারপর QAOA এর কাছে প্রেরণ করা যেতে পারে।
[14]:
ws_qaoa_mes = QAOA(
sampler=Sampler(),
optimizer=COBYLA(),
initial_state=init_qc,
mixer=ws_mixer,
initial_point=[0.0, 1.0],
)
[15]:
ws_qaoa = MinimumEigenOptimizer(ws_qaoa_mes)
[16]:
ws_qaoa_result = ws_qaoa.solve(qubo)
print(ws_qaoa_result.prettyprint())
objective function value: 16.768932200000002
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS
বিশ্লেষণ#
উভয় ফলাফল একই ফলাফল দিতে প্রদর্শিত হবে। যাইহোক, যখন আমরা অন্তর্নিহিত সম্ভাব্যতা বিতরণের দিকে তাকাই তখন আমরা লক্ষ্য করি যে উষ্ণ-শুরু QAOA এর সর্বোত্তম সমাধানের নমুনা দেওয়ার সম্ভাবনা অনেক বেশি।
[17]:
def format_qaoa_samples(samples, max_len: int = 10):
qaoa_res = []
for s in samples:
if sum(s.x) == 3:
qaoa_res.append(("".join([str(int(_)) for _ in s.x]), s.fval, s.probability))
res = sorted(qaoa_res, key=lambda x: -x[1])[0:max_len]
return [(_[0] + f": value: {_[1]:.3f}, probability: {1e2*_[2]:.1f}%") for _ in res]
format_qaoa_samples(qaoa_result.samples)
[17]:
['001110: value: 16.769, probability: 0.7%',
'011010: value: 15.744, probability: 0.7%',
'001011: value: 14.671, probability: 0.6%',
'101010: value: 14.626, probability: 0.7%',
'010110: value: 14.234, probability: 2.3%',
'100110: value: 13.953, probability: 1.6%',
'000111: value: 13.349, probability: 1.5%',
'110010: value: 12.410, probability: 3.0%',
'010011: value: 12.013, probability: 2.7%',
'100011: value: 11.559, probability: 3.3%']
[18]:
format_qaoa_samples(ws_qaoa_result.samples)
[18]:
['001110: value: 16.769, probability: 72.8%',
'001011: value: 14.671, probability: 1.2%',
'101010: value: 14.626, probability: 2.6%',
'100110: value: 13.953, probability: 0.3%',
'000111: value: 13.349, probability: 0.1%',
'100011: value: 11.559, probability: 0.0%']
কিউএওএ (QAOA) এর প্রস্তুতি#
উপরের উষ্ণ-শুরু বৈশিষ্ট্যগুলি কিস্কিট অপ্টিমাইজেশান মডিউলে WarmStartQAOAOptimizer নামে একটি একক অপ্টিমাইজার হিসাবে উপলব্ধ যা নীচে চিত্রিত করা হয়েছে। এই সমাধানকারী একটি উষ্ণ-শুরু QAOA দিয়ে একটি QUBO সমাধান করবে। এটি সমস্যাকে শিথিল করে \(c^*\) গণনা করে। এই আচরণ relax_for_pre_solver থেকে True সেট করে নিয়ন্ত্রিত হয়।
[19]:
from qiskit_optimization.algorithms import WarmStartQAOAOptimizer
[20]:
qaoa_mes = QAOA(sampler=Sampler(), optimizer=COBYLA(), initial_point=[0.0, 1.0])
ws_qaoa = WarmStartQAOAOptimizer(
pre_solver=CplexOptimizer(), relax_for_pre_solver=True, qaoa=qaoa_mes, epsilon=0.0
)
[21]:
ws_result = ws_qaoa.solve(qubo)
print(ws_result.prettyprint())
objective function value: 16.768932200000002
variable values: x0=0.0, x1=0.0, x2=1.0, x3=1.0, x4=1.0, x5=0.0
status: SUCCESS
[22]:
format_qaoa_samples(ws_result.samples)
[22]:
['001110: value: 16.769, probability: 72.8%',
'001011: value: 14.671, probability: 1.2%',
'101010: value: 14.626, probability: 2.6%',
'100110: value: 13.953, probability: 0.3%',
'000111: value: 13.349, probability: 0.1%',
'100011: value: 11.559, probability: 0.0%']
[23]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Software | Version |
|---|---|
qiskit | 0.45.1 |
qiskit_algorithms | 0.2.1 |
qiskit_optimization | 0.7.0 |
| System information | |
| Python version | 3.10.13 |
| Python compiler | GCC 13.2.1 20230728 (Red Hat 13.2.1-1) |
| Python build | main, Aug 28 2023 00:00:00 |
| OS | Linux |
| CPUs | 12 |
| Memory (Gb) | 31.056411743164062 |
| Wed Dec 06 10:26:59 2023 CET | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: