নোট

এই পৃষ্ঠাটি docs/tutorials/05_admm_optimizer.ipynb থেকে বানানো হয়েছে।

এ ডি এম এম অনুকূলায়ক (অপ্টিমাইজার)#

ভূমিকা#

এডিএমএম অপ্টিমাইজার মিশ্র-বাইনারি সীমাবদ্ধ অপ্টিমাইজেশন সমস্যার ক্লাস সমাধান করতে পারে, এরপরে (এমবিসিও), যা প্রায়শই লজিস্টিক, ফাইন্যান্স এবং অপারেশন গবেষণায় উপস্থিত হয়। বিশেষত, এখানে নির্মিত এডিএমএম অপ্টিমাইজার নিম্নলিখিত অপ্টিমাইজেশান সমস্যাটি মোকাবেলা করতে পারে $(P)$:

\[\min_{x \in \mathcal{X},u\in\mathcal{U} \subseteq \mathbb{R}^l } \quad q(x) + \varphi(u),\]

সীমাবদ্ধতার সাপেক্ষে:

\[\mathrm{s.t.:~} \quad G x = b, \quad g(x) \leq 0, \quad \ell(x, u) \leq 0,\]

সংশ্লিষ্ট কার্যকরী অনুমানের সাথে।

ফাংশন $q: \mathbb{R}^n \to \mathbb{R}$ হল দ্বিঘাত (কোয়াড্রাটিক), অর্থাৎ, $q(x) = x^{\intercal} Q x + a^{\intercal} x$ একটি প্রদত্ত সমান্ত্রিক বর্গাকার ম্যাট্রিক্সের জন্য $Q \in \mathbb{R}^n \times \mathbb{R}^n, Q = Q^{\intercal}$, এবং ভেক্টর $a \in \mathbb{R}^n$;
সেট $\mathcal{X} = \{0,1\}^n = \{x_{(i)} (1-x_{(i)}) = 0, \forall i\}$ দ্বিমিক (বাইনারি) সীমাবদ্ধতা প্রবর্তন করে;
ম্যাট্রিক্স $G\in\mathbb{R}^n \times \mathbb{R}^{n'}$, ভেক্টর $b \in \mathbb{R}^{n'}$, এবং ফাংশন $g: \mathbb{R}^n \to \mathbb{R}$ হল উত্তল;
ফাংশন $\varphi: \mathbb{R}^l \to \mathbb{R}$ উত্তল এবং $\mathcal{U}$ একটি উত্তল সেট;
ফাংশন $\ell: \mathbb{R}^n\times \mathbb{R}^l \to \mathbb{R}$ হল যৌথভাবে $x, u$ এ উত্তল।

এমবিও সমস্যাগুলি সমাধান করার জন্য, [1] প্রস্তাবিত হিউরিস্টিক্স $(P)$ মাল্টিপ্লায়ার্সের বিকল্প দিকনির্দেশ পদ্ধতির উপর ভিত্তি করে (এডিএমএম) [2]। এডিএমএম হ’ল উত্তল অপ্টিমাইজেশনের দীর্ঘ ইতিহাস সহ একটি অপারেটর বিভক্ত অ্যালগরিদম, এবং এটি অবশিষ্ট, উদ্দেশ্য এবং দ্বৈত ভেরিয়েবল কনভার্জেন্স বৈশিষ্ট্য হিসাবে পরিচিত, যদি উত্তল অনুমানের ধারণা থাকে।

The method of [1] (referred to as 3-ADMM-H) leverages the ADMM operator-splitting procedure to devise a decomposition for certain classes of MBOs into:

a QUBO subproblem to be solved by on the quantum device via variational algorithms, such as VQE or QAOA;
continuous convex constrained subproblem, which can be efficiently solved with classical optimization solvers.

অ্যালগরিদম 3-ADMM-H নিম্নলিখিত উপায়ে কাজ করে:

প্রারম্ভিক পর্যায় (স্থিতিমাপ, QUBO আর কনভেক্স সমাধানকারক গুলি নির্ণয় করা);
সমাপ্তি না হওয়ার পূর্বে প্রতিটি এডিএমএম পুনরাবৃত্তির জন্য ($k = 1, 2, \ldots, $) ব্যবহার করা হয়
- একটি সঠিকভাবে সংজ্ঞায়িত QUBO উপ -সমস্যার সমাধান করুন (একটি শাস্ত্রীয় বা কোয়ান্টাম সমাধানকারী সহ);
- সঠিকভাবে সংজ্ঞায়িত উত্তল সমস্যার সমাধান করুন (একটি শাস্ত্রীয় সমাধানকারী সহ);
- দ্বৈত ভেরিয়েবল আপডেট করুন।
অপ্টিমাইজার এবং খরচ ফেরত (রিটার্ন) নেওয়া

অ্যালগরিদমের অভিন্নতা, সম্ভাব্যতা এবং অনুকূলতার শর্তাবলী সম্পর্কে একটি বিস্তৃত আলোচনা পাওয়া যাবে [1]। 2 এডিএমএম ব্লকের একটি বৈকল্পিক, যেমন একটি কিউইউবিও (QUBO) উপ -সমস্যা, এবং একটি ক্রমাগত উত্তল সীমাবদ্ধ সাব -সমস্যা, [1] তেও চালু করা হয়েছে।

তথ্যসূত্র#

[1] C. Gambella and A. Simonetto, Multi-block ADMM heuristics for mixed-binary optimization, on classical and quantum computers, arXiv preprint arXiv:2001.02069 (2020).

[2] S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, Distributed optimization and statistical learning via the alternating direction method of multipliers, Foundations and Trends in Machine learning, 3, 1–122 (2011).

আরম্ভ#

প্রথমত আমরা আমাদের প্রয়োজনীয় সমস্ত প্যাকেজ লোড করি।

[1]:

import matplotlib.pyplot as plt

from docplex.mp.model import Model

from qiskit_algorithms import QAOA, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import COBYLA
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import CobylaOptimizer, MinimumEigenOptimizer
from qiskit_optimization.algorithms.admm_optimizer import ADMMParameters, ADMMOptimizer
from qiskit_optimization.translators import from_docplex_mp

# If CPLEX is installed, you can uncomment this line to import the CplexOptimizer.
# CPLEX can be used in this tutorial to solve the convex continuous problem,
# but also as a reference to solve the QUBO, or even the full problem.
#
# from qiskit.optimization.algorithms import CplexOptimizer

এই টিউটোরিয়ালে আমরা প্রথমে যে অ্যালগরিদমগুলি ব্যবহার করার পরিকল্পনা করি তা আমরা প্রথমে শুরু করি।

To solve the QUBO problems we can choose between

MinimumEigenOptimizer using different MinimumEigensolver, such as SamplingVQE, QAOA or NumpyMinimumEigensolver (classical)
GroverOptimizer
CplexOptimizer (classical, if CPLEX is installed)

and to solve the convex continuous problems we can choose between the following classical solvers:

CplexOptimizer (if CPLEX is installed)
CobylaOptimizer

যদি CPLEX পাওয়া না যায়, "CobylaOptimizer" (উত্তল ক্রমাগত সমস্যার জন্য) এবং NumpyMinimumEigensolver (QUBOs এর জন্য) ব্যবহার করে MinimumEigenOptimizer পরীক্ষা, বৈধতা এবং বেঞ্চমার্কিংয়ের জন্য CPLEX এর শাস্ত্রীয় বিকল্প হিসাবে ব্যবহার করা যেতে পারে।

[2]:

# define COBYLA optimizer to handle convex continuous problems.
cobyla = CobylaOptimizer()

# define QAOA via the minimum eigen optimizer
qaoa = MinimumEigenOptimizer(QAOA(sampler=Sampler(), optimizer=COBYLA()))

# exact QUBO solver as classical benchmark
exact = MinimumEigenOptimizer(NumPyMinimumEigensolver())  # to solve QUBOs

# in case CPLEX is installed it can also be used for the convex problems, the QUBO,
# or as a benchmark for the full problem.
#
# cplex = CplexOptimizer()

উদাহরণ#

আমরা 3-ADMM-H অ্যালগরিদম একটি সাধারণ মিশ্র-বাইনারি দ্বিঘাত (কোয়াড্রাটিক) সমস্যা সমতা এবং অসমতার সীমাবদ্ধতার সাথে পরীক্ষা করি (উদাহরণ 6 [1] এ রিপোর্ট করা হয়েছে)। আমরা প্রথমে একটি ডকপ্লেক্স সমস্যা তৈরি করি এবং তারপর এটি একটি QuadraticProgram লোড করি।

[3]:

# construct model using docplex
mdl = Model("ex6")

v = mdl.binary_var(name="v")
w = mdl.binary_var(name="w")
t = mdl.binary_var(name="t")
u = mdl.continuous_var(name="u")

mdl.minimize(v + w + t + 5 * (u - 2) ** 2)
mdl.add_constraint(v + 2 * w + t + u <= 3, "cons1")
mdl.add_constraint(v + w + t >= 1, "cons2")
mdl.add_constraint(v + w == 1, "cons3")

# load quadratic program from docplex model
qp = from_docplex_mp(mdl)
print(qp.prettyprint())

Problem name: ex6

Minimize
  5*u^2 + t - 20*u + v + w + 20

Subject to
  Linear constraints (3)
    t + u + v + 2*w <= 3  'cons1'
    t + v + w >= 1  'cons2'
    v + w == 1  'cons3'

  Continuous variables (1)
    0 <= u

  Binary variables (3)
    v w t

ক্লাসিকাল সমাধান#

3-ADMM-H needs a QUBO optimizer to solve the QUBO subproblem, and a continuous optimizer to solve the continuous convex constrained subproblem. We first solve the problem classically: we use the MinimumEigenOptimizer with the NumPyMinimumEigenSolver as a classical and exact QUBO solver and we use the CobylaOptimizer as a continuous convex solver. 3-ADMM-H supports any other suitable solver available in Qiskit optimization. For instance, SamplingVQE, QAOA, and GroverOptimizer can be invoked as quantum solvers, as demonstrated later. If CPLEX is installed, the CplexOptimizer can also be used as both, a QUBO and convex solver.

পরামিতি#

3-ADMM-H শ্রেণী ADMMParameters এ আবৃত। কাস্টমাইজড প্যারামিটার মান ক্লাসের আর্গুমেন্ট হিসাবে সেট করা যেতে পারে। এই উদাহরণে, প্যারামিটার $\rho, \beta$ কে যথাক্রমে $1001$ এবং $1000$ এ শুরু করা হয়েছে। সমতা সীমাবদ্ধতার factor_c শাস্তি $Gx = b$ সেট করা হয়েছে $900$। মৌলিক অবশিষ্ট কনভারজেন্সের জন্য সহনশীলতা tol কে 1.e-6 তে সেট করা আছে। এই ক্ষেত্রে, 3-ব্লক বাস্তবায়ন [1] এর 4 তত্ত্বের জন্য একত্রিত হওয়ার গ্যারান্টিযুক্ত, কারণ অবিচ্ছিন্ন পরিবর্তনশীলতার সাথে অসমতার সীমাবদ্ধতা সর্বদা সক্রিয় থাকে। 2-ব্লক বাস্তবায়ন three_block=False সেট করে চালানো যেতে পারে, এবং কার্যত একটি সম্ভাব্য নয় অনুকূল সমাধানের জন্য রূপান্তরিত হয়।

[4]:

admm_params = ADMMParameters(
    rho_initial=1001, beta=1000, factor_c=900, maxiter=100, three_block=True, tol=1.0e-6
)

3-ADMM-H অ্যালগরিদম কল করা#

3-ADMM-H অ্যালগরিদম আহবান করার জন্য, ADMMOptimizer শ্রেণীর একটি উদাহরণ তৈরি করা প্রয়োজন। এটি ADMM- specific পরামিতি এবং উপ-সমস্যা অপ্টিমাইজারগুলিকে আলাদাভাবে কনস্ট্রাক্টরের মধ্যে নিয়ে যায়। সমাধানটি OptimizationResult শ্রেণীর একটি উদাহরণ।

[5]:

# define QUBO optimizer
qubo_optimizer = exact
# qubo_optimizer = cplex  # uncomment to use CPLEX instead

# define classical optimizer
convex_optimizer = cobyla
# convex_optimizer = cplex  # uncomment to use CPLEX instead

# initialize ADMM with classical QUBO and convex optimizer
admm = ADMMOptimizer(
    params=admm_params, qubo_optimizer=qubo_optimizer, continuous_optimizer=convex_optimizer
)

[6]:

# run ADMM to solve problem
result = admm.solve(qp)

ক্লাসিকাল সমাধান এর উত্তর#

3-ADMM-H সমাধান তারপর মুদ্রিত এবং কল্পনা করা যেতে পারে। সমাধানের x অ্যাট্রিবিউট যথাক্রমে, বাইনারি সিদ্ধান্ত ভেরিয়েবলের মান এবং ক্রমাগত সিদ্ধান্ত ভেরিয়েবলের মান রয়েছে। Fval হল সমাধানের উদ্দেশ্য মান।

[7]:

print(result.prettyprint())

objective function value: 1.0
variable values: v=1.0, w=0.0, t=0.0, u=2.0
status: SUCCESS

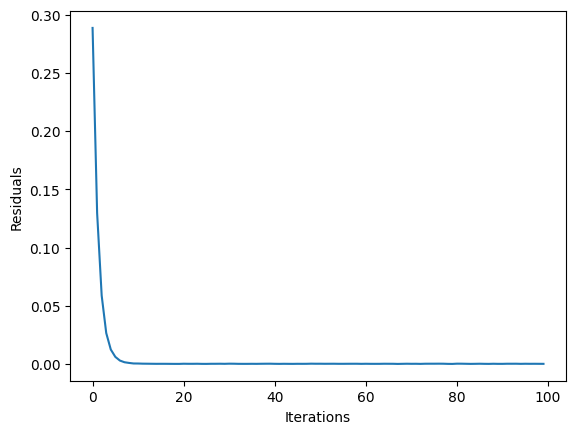
সমাধান পরিসংখ্যান state ক্ষেত্রে অ্যাক্সেস করা যেতে পারে এবং দৃশ্যায়িত করা যায়। আমরা এখানে প্রাথমিক অবশিষ্টাংশের পরিপ্রেক্ষিতে 3-ADMM-H এর সংমিশ্রণ প্রদর্শন করি।

[8]:

plt.plot(result.state.residuals)
plt.xlabel("Iterations")
plt.ylabel("Residuals")
plt.show()

../_images/tutorials_05_admm_optimizer_19_0.png

কোয়ান্টাম সমাধান#

সিমুলেটেড কোয়ান্টাম ডিভাইসে চলমান আমরা এখন QUBO অপটিমাইজার হিসাবে QAOA এর সাথে একই অপটিমাইজেশন সমস্যাটি সমাধান করি। প্রথমে, eigensolver দিয়ে QAOA ক্লাসিকাল অপ্টিমাইজার নির্বাচন করা দরকার। তারপরে, সিমুলেশন ব্যাকএন্ড সেট করা আছে। শেষ অবধি, eigensolver টি `` ন্যূনতমএইগেন অপটিমাইজার `` শ্রেণিতে আবৃত হয়। ADMMOptimizer এর নতুন instance টি QAOA আর QUBO অপ্টিমাইজার দিয়ে সমৃদ্ধ।

[9]:

# define QUBO optimizer
qubo_optimizer = qaoa

# define classical optimizer
convex_optimizer = cobyla
# convex_optimizer = cplex  # uncomment to use CPLEX instead

# initialize ADMM with quantum QUBO optimizer and classical convex optimizer
admm_q = ADMMOptimizer(
    params=admm_params, qubo_optimizer=qubo_optimizer, continuous_optimizer=convex_optimizer
)

[10]:

# run ADMM to solve problem
result_q = admm_q.solve(qp)

কোয়ান্টাম সমাধানকারক এর ফলাফল#

এখানে আমরা কোয়ান্টাম সমাধানকারক এর ফলাফল গুলি উপস্থাপন করলাম. উপরের উদাহরণ এ x হলো সমাধান এবং fval উদ্দেশ্য মান হিসাবে চিহ্নিত।

[11]:

print(result.prettyprint())

objective function value: 1.0
variable values: v=1.0, w=0.0, t=0.0, u=2.0
status: SUCCESS

[12]:

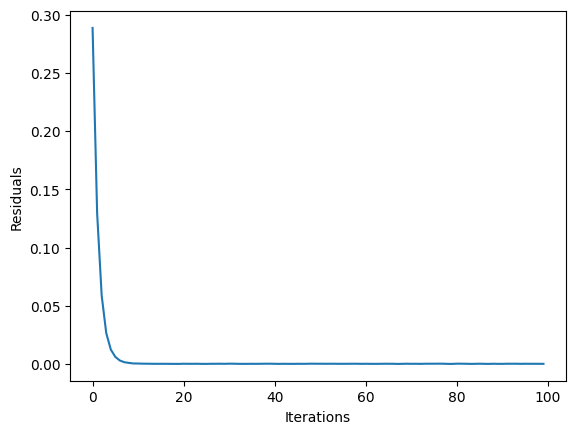
plt.clf()
plt.plot(result_q.state.residuals)
plt.xlabel("Iterations")
plt.ylabel("Residuals")
plt.show()

../_images/tutorials_05_admm_optimizer_25_0.png

[13]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
`qiskit-terra`	0.23.0
`qiskit-aer`	0.11.1
`qiskit-optimization`	0.5.0
`qiskit-machine-learning`	0.6.0
System information
Python version	3.9.15
Python compiler	Clang 14.0.0 (clang-1400.0.29.102)
Python build	main, Oct 11 2022 22:27:25
OS	Darwin
CPUs	4
Memory (Gb)	16.0
Tue Dec 06 21:47:54 2022 JST

This code is a part of Qiskit

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.

[ ]: