注釈
このページは docs/tutorials/05_admm_optimizer.ipynb から生成されました。
ADMM オプティマイザー#
はじめに#
ADMMオプティマイザーは、ロジスティック、金融、オペレーションズ・リサーチに多く見られる、混合バイナリー制約の最適化問題(以下MBCO)のクラスを解くことができます。 特に、ここで設計された ADMMオプティマイザーは、次の最適化問題 \((P)\) に取り組むことができます。
制約の対象:
対応する機能的な仮定に基づいています
関数 \(q: \mathbb{R}^n \to \mathbb{R}\) は二次です。つまり、対称正方行列 \(Q \in \mathbb{R}^n \times \mathbb{R}^n, Q = Q^{\intercal}\) と ベクトル \(a \in \mathbb{R}^n\) について、 \(q(x) = x^{\intercal} Q x + a^{\intercal} x\) です。
\(\mathcal{X} = \{0,1\}^n = \{x_{(i)} (1-x_{(i)}) = 0, \forall i\}\) により、バイナリー制約が強制されます。
行列 \(G\in\mathbb{R}^n \times \mathbb{R}^{n'}\), ベクトル \(b \in \mathbb{R}^{n'}\), および関数 \(g: \mathbb{R}^n \to \mathbb{R}\) は、凸です。
関数 \(\varphi: \mathbb{R}^l \to \mathbb{R}\) は凸で、 \(\mathcal{U}\) は凸集合です。
関数 \(\ell: \mathbb{R}^n\times \mathbb{R}^l \to \mathbb{R}\) は \(x, u\) について 一体で 凸です。
MBO問題を解くために、[1]は Alternating Direction Method of Multipliers(交互方向乗数法, ADMM)[2]に基づいて \((P)\) についてのヒューリスティックスを提案しました。ADMMは、凸最適化の長い歴史を持つ演算子分割アルゴリズムであり、凸性の仮定が成り立つ場合、残差、目的関数、および双対変数収束の特性を持つことが知られています。
[1] の方法(3-ADMM-H と呼ばれる)は、ADMM演算子分割手順を利用して、特定のクラスの MBO を次のように分解します。
VQE や QAOA などの変分アルゴリズムを介して量子デバイス上で解決されるQUBOサブ問題。
古典的最適化ソルバーで効率的に解くことができる連続凸制約付きサブ問題。
アルゴリズム 3-ADMM-H は以下のように動作します。
初期化フェーズ (パラメーターとQUBOと凸ソルバーを設定);
ADMM の各反復($k = 1, 2, \ldots, $) を、終了するまで行います:
適切に定義された QUBO サブ問題を (古典または量子ソルバーで) 解く;
適切に定義された凸問題を(古典ソルバーで) 解く;
双対変数を更新する
オプティマイザーとコストを返す
アルゴリズムの収束、実現可能性、および最適化の条件に関する包括的な議論は、[1]にあります。 2つのADMMブロックを持つバリアント、つまりQUBOサブ問題と連続凸制約付きサブ問題も[1]で紹介されています。
参考文献#
初期化#
まず、必要なパッケージをすべてロードします。
[1]:
import matplotlib.pyplot as plt
from docplex.mp.model import Model
from qiskit_algorithms import QAOA, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import COBYLA
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import CobylaOptimizer, MinimumEigenOptimizer
from qiskit_optimization.algorithms.admm_optimizer import ADMMParameters, ADMMOptimizer
from qiskit_optimization.translators import from_docplex_mp
# If CPLEX is installed, you can uncomment this line to import the CplexOptimizer.
# CPLEX can be used in this tutorial to solve the convex continuous problem,
# but also as a reference to solve the QUBO, or even the full problem.
#
# from qiskit.optimization.algorithms import CplexOptimizer
最初に、このチュートリアルで後で使用する予定のすべてのアルゴリズムを初期化します。
QUBOの問題を解決するために、次のいずれかを選択できます。
SamplingVQE、QAOA、NumpyMinimumEigensolver(古典) などのさまざまなMinimumEigensolverを使用するMinimumEigenOptimizerGroverOptimizerCplexOptimizer(CPLEXがインストールされている場合は古典)
そして、凸の連続的な問題を解決するために、次の古典ソルバーのどちらかを選択できます。
CplexOptimizer(CPLEXがインストールされている場合)CobylaOptimizer
CPLEXが利用できない場合、CPLEXの古典的な代替として、凸連続問題であれば CobylaOptimizer を、QUBOであれば NumpyMinimumEigensolver を用いた MinimEigenOptimizer を使用して、テスト、検証、ベンチマークを行うことができます。
[2]:
# define COBYLA optimizer to handle convex continuous problems.
cobyla = CobylaOptimizer()
# define QAOA via the minimum eigen optimizer
qaoa = MinimumEigenOptimizer(QAOA(sampler=Sampler(), optimizer=COBYLA()))
# exact QUBO solver as classical benchmark
exact = MinimumEigenOptimizer(NumPyMinimumEigensolver()) # to solve QUBOs
# in case CPLEX is installed it can also be used for the convex problems, the QUBO,
# or as a benchmark for the full problem.
#
# cplex = CplexOptimizer()
例#
3-ADMM-Hアルゴリズムを、等式や不等式制約をもつ簡単な混合バイナリー二次計画問題でテストします([1] の例6)。 最初にdocplex問題を構築し、次にそれを QuadraticProgram にロードします。
[3]:
# construct model using docplex
mdl = Model("ex6")
v = mdl.binary_var(name="v")
w = mdl.binary_var(name="w")
t = mdl.binary_var(name="t")
u = mdl.continuous_var(name="u")
mdl.minimize(v + w + t + 5 * (u - 2) ** 2)
mdl.add_constraint(v + 2 * w + t + u <= 3, "cons1")
mdl.add_constraint(v + w + t >= 1, "cons2")
mdl.add_constraint(v + w == 1, "cons3")
# load quadratic program from docplex model
qp = from_docplex_mp(mdl)
print(qp.prettyprint())
Problem name: ex6
Minimize
5*u^2 + t - 20*u + v + w + 20
Subject to
Linear constraints (3)
t + u + v + 2*w <= 3 'cons1'
t + v + w >= 1 'cons2'
v + w == 1 'cons3'
Continuous variables (1)
0 <= u
Binary variables (3)
v w t
古典的解法#
3-ADMM-Hは、QUBOサブ問題を解くのにはQUBOオプティマイザーを、連続凸制約問題を解くのには連続オプティマイザーを必要とします。まず最初に、問題を古典的な方法で解きます: NumPyMinimumEigenSolver による MinimumEigenOptimizer を古典的かつ正確な QUBO ソルバーとして使用し、連続凸問題ソルバーとして CobylaOptimizer を使用します。 3-ADMM-Hは、他にもQiskit optimizationで利用可能な適切なソルバーをすべてサポートしています。例えば、SamplingVQE 、 QAOA 、 GroverOptimizer は、後述するように、量子ソルバーとして呼び出すことができます。 CPLEXがインストールされていれば、CplexOptimizer をQUBOと凸ソルバーのいずれにも使用することができます。
パラメーター#
3-ADMM-Hは、 ADMMParameters クラスにラップされています。カスタマイズされたパラメーター値は、クラスの引数として設定できます。この例では、パラメーター \(\rho, \beta\) がそれぞれ \(1001\) と \(1000\) に初期化されています。等式制約 \(Gx = b\) のペナルティ factor_c は \(900\) に設定されています。一次残差収束の許容誤差 tol は 1.e-6 に設定されています。この場合、3変数の実装は、[1]の定理4に対して収束することが保証されています。これは、連続変数による不等式制約が常にアクティブであるためです。2ブロックの実装は three_block=False を設定することで実行でき、最適ではない実行可能解に実質的に収束します。
[4]:
admm_params = ADMMParameters(
rho_initial=1001, beta=1000, factor_c=900, maxiter=100, three_block=True, tol=1.0e-6
)
3-ADMM-Hアルゴリズムを呼び出す#
3-ADMM-H アルゴリズムを呼び出すには、ADMMOptimizer クラスのインスタンスを作成する必要があります。 これにより、ADMM固有のパラメータとサブ問題のオプティマイザがコンストラクターに分離されます。返されるソリューションは、OptimizationResult クラスのインスタンスです。
[5]:
# define QUBO optimizer
qubo_optimizer = exact
# qubo_optimizer = cplex # uncomment to use CPLEX instead
# define classical optimizer
convex_optimizer = cobyla
# convex_optimizer = cplex # uncomment to use CPLEX instead
# initialize ADMM with classical QUBO and convex optimizer
admm = ADMMOptimizer(
params=admm_params, qubo_optimizer=qubo_optimizer, continuous_optimizer=convex_optimizer
)
[6]:
# run ADMM to solve problem
result = admm.solve(qp)
古典ソルバーの結果#
3-ADMM-Hソリューションをプリントして可視化することができます。 解の x 属性には、バイナリー決定変数の値と連続決定変数の値がそれぞれ含まれています。 fval はその解の目的値です。
[7]:
print(result.prettyprint())
objective function value: 1.0
variable values: v=1.0, w=0.0, t=0.0, u=2.0
status: SUCCESS
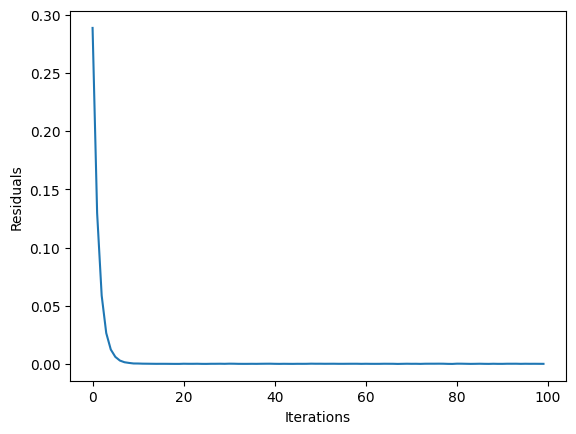
state フィールドで解の解析統計にアクセスし可視化することができます。ここでは、原始残差の観点から、3-ADMM-Hの収束を示します。
[8]:
plt.plot(result.state.residuals)
plt.xlabel("Iterations")
plt.ylabel("Residuals")
plt.show()
量子ソリューション#
シミュレートされた量子デバイス上で実行されるQUBOオプティマイザーと同じQAOAの最適化問題を解決します。まず、固有値ソルバーQAOAの古典的なオプティマイザーを選択する必要があります。次に、シミュレーションバックエンドが設定されます。最後に、固有ソルバーは MinimumEigenOptimizer クラスにラップされます。 ADMMOptimizer の新しいインスタンスには、QUBOオプティマイザーとしてQAOAが入力されます。
[9]:
# define QUBO optimizer
qubo_optimizer = qaoa
# define classical optimizer
convex_optimizer = cobyla
# convex_optimizer = cplex # uncomment to use CPLEX instead
# initialize ADMM with quantum QUBO optimizer and classical convex optimizer
admm_q = ADMMOptimizer(
params=admm_params, qubo_optimizer=qubo_optimizer, continuous_optimizer=convex_optimizer
)
[10]:
# run ADMM to solve problem
result_q = admm_q.solve(qp)
量子ソルバーの結果#
ここでは、量子ソルバーから得られた結果を紹介します。 上の例のように、x はソリューションの略で、fval は目的値を表します。
[11]:
print(result.prettyprint())
objective function value: 1.0
variable values: v=1.0, w=0.0, t=0.0, u=2.0
status: SUCCESS
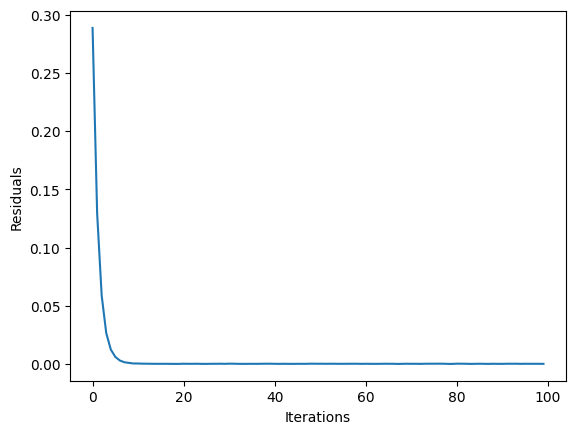
[12]:
plt.clf()
plt.plot(result_q.state.residuals)
plt.xlabel("Iterations")
plt.ylabel("Residuals")
plt.show()
[13]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.23.0 |
qiskit-aer | 0.11.1 |
qiskit-optimization | 0.5.0 |
qiskit-machine-learning | 0.6.0 |
| System information | |
| Python version | 3.9.15 |
| Python compiler | Clang 14.0.0 (clang-1400.0.29.102) |
| Python build | main, Oct 11 2022 22:27:25 |
| OS | Darwin |
| CPUs | 4 |
| Memory (Gb) | 16.0 |
| Tue Dec 06 21:47:54 2022 JST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2022.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: