注釈
このページは docs/tutorials/07_examples_vehicle_routing.ipynb から生成されました。
配車ルーティング#
はじめに#
ロジスティクスは主要産業であり、2015年には世界全体で8兆1830億米ドルになるという推計もあります。ほとんどのサービスプロバイダーは、多数の車両(トラックやコンテナ船など)、車両が夜間に拠点とする多数のデポを運営しています。 車両は夜間にはデポを拠点とし、毎日、各車両で多くのクライアントの場所にサービスを提供します。 これらのパラメータを考慮する最適化および制御の問題がたくさんあります。 計算上の重要な課題は、デポから多数のクライアントの場所に行ってまたデポに戻るルートをどのように設計すれば、車両の走行距離、費やした時間、またはそれに類する目的関数を最小にすることができるか、ということです。 このノートブックでは、理想化された形の問題を定式化し、Farhi, Goldstone, and Gutman(2014)の量子近似最適化アプローチを使用してその解決策を紹介します。
全体的なワークフローは以下のとおりです。
クライアントの場所を確立します。 通常、これらはデータベースからの配信日の前に利用可能です。 私たちのユースケースでは、これらをランダムに生成します。
ペアワイズ距離、移動時間などを計算します。 私たちの場合、「カラスが飛ぶように」ユークリッド距離を考慮します。これはおそらく最も単純な距離です。
実際のルートを計算します。 このステップは、実際には2回実行されます。 最初に、古典的なコンピューターで古典的なソルバー(IBM CPLEX)を実行して参照値を取得します。 次に、量子コンピューターで部分的に代替のハイブリッドアルゴリズムを実行します。
結果を視覚化します。 ここでは単純なプロットをします。
以下では、前提条件のインストールとデータのロードに進む前に、まずモデルについて説明します。
モデル#
数学的に言えば、配車ルート問題(vehicle routing problem、VRP)は組み合わせ問題であり、利用可能な車両の数を考慮して、デポから多数のクライアントに戻り、デポに戻る最適なルートが求められます。 巡回セールスマン問題の多くの定式化を拡張して、可能な多くの定式化があります [Applegate et al, 2006] 。 ここでは、MTZ [Miller, Tucker, Zemlin, 1960] として知られる定式化を紹介します。
\(n\) をクライアントの数( \(1,\dots,n\) としてインデックス付け)、 \(K\) を利用可能な車両の数とします。 \(x_{ij} = \{0,1\}\) をバイナリー決定変数とします。これが \(1\) の場合、ノード \(i\) からノード \(j\) へのセグメントをアクティブにします。 ノードインデックスは \(0\) から \(n\) まで実行されます。ここで、 \(0\) は(慣例により)デポです。 エッジの2倍の異なる決定変数があります。 たとえば、完全接続されたグラフには、 \(n(n+1)\) 個のバイナリ決定変数があります。
2つのノード \(i\) と \(j\) に \(i\) から \(j\) へのリンクがある場合、 \(i \sim j\) と記述します。 また、 \(i \sim j\) の場合に限り、 \(i\) がリンクしているノードのセットを \(\delta(i)^+\) で表します。つまり、\(j \in \delta(i)^+\) です。 同様に、 \(j \sim i\) の場合に限り、 \(j \in \delta(i)^-\) という意味で、iに接続されているノードのセットを \(\delta(i)^-\) で表します。
さらに、 \(u_i\) で表されるすべてのノード \(i = 1,\dots, n\) について、連続変数を検討します。 これらの変数は、クライアント間のサブツアーを排除するために、問題のMTZ定式化で必要です。
VRPは以下のように定式化できます:
ノード訪問制約の対象:
デポ訪問の制約:
およびサブツアー除去の制約:
特に、
コスト関数はコスト関数で線形であり、正の重み \(w_{ij}>0\) に基づいてさまざまなアーチの重みを付けます。(通常、ノード \(i\) とノード \(j\) の間の距離)
最初の一連の制約は、すべてのクライアントとの間で、1つのリンクのみが許可されることを強制します。
制約の2番目のセットは、デポとの間で正確に \(K\) 個のリンクが許可されることを強制します。
制約の3番目のセットは、サブツアー除去制約を適用し、 \(Q>q_j>0\) および \(Q,q_i \in \mathbb{R}\) を使用して \(u_i\) の境界になります。
古典的なソリューション#
CPLEXを使用するなどして、VRPを古典的に解決できます。 CPLEXは、branch-and-bound-and-cut 法を使用して、VRPの近似解を見つけます。これは、この定式化では、混合整数線形計画(mixed-integer linear program、MILP)です。 表記のために、決定変数を1つのベクトルに次のようにパックします。
ここでは、 \({\bf z} \in \{0,1\}^N\) 、 \(N = n (n+1)\) です。 したがって、問題の次元はノードの数に比例して二次関数的にスケーリングします。 最適解を \({\bf z}^*\) で表し、関連する最適コストを \(f^*\) で表します。
量子ソリューション#
ここでは、Farhi, Goldstone, and Gutman(2014)の量子近似最適化アプローチに従って、古典的な計算ステップと量子的な計算ステップを組み合わせたアプローチを示します。 特に、変分量子固有値ソルバー(variational quantum eigensolver、VQE)を使用します。 強調しておきたいのは、使用できる量子回路の深さが限られていること(変分形式)を考えると、アルゴリズムの高速化について議論するのは難しいということです。というのは、得られる解は本質的にヒューリスティックなものとなるからです。 同時に、対象となる問題の性質と重要性のため、ヒューリスティックなアプローチについて調べるのは価値のあることです。いくつかの問題クラスではこれが有用でしょう。
アルゴリズムは以下のように要約できます:
準備ステップ:
組合せ最適化問題を、等式制約のみでバイナリー多項式最適化問題に変換します。
変数 \({\bf z}\) および基底 \(Z\) のイジング・ハミルトニアン (\(H\)) に、必要ならばペナルティー・メソッドを使用して、結果の問題をマップします。
量子回路の深さ \(m\) を選択します。 深さは適応的に変更できることに注意してください。
コントロール \(\theta\) のセットを選択し、 \(\boldsymbol\theta\) の成分によってパラメータ化された、制御位相ゲートと単一量子ビットY回転ゲートで構成される量子回路を使用して構築された、試行関数 \(\big|\psi(\boldsymbol\theta)\rangle\) を作成します。
アルゴリズムの手順:
Z基底で回路の結果をサンプリングし、個々のイジング項の期待値を合計して、 \(C(\boldsymbol\theta) = \langle\psi(\boldsymbol\theta)\big|H\big|\psi(\boldsymbol\theta)\rangle\) を評価します。 一般に、選択した古典的なオプティマイザーに応じて、 \(\boldsymbol\theta\) 周辺のさまざまな制御点を推定する必要があります。
古典的なオプティマイザーを使用して、新しいコントロールのセットを選択します。
\(C(\boldsymbol\theta)\) が最小値に達するまで続け、解 \(\boldsymbol\theta^*\) に十分に近づけます。
最後の \(\boldsymbol\theta\) を使用して、分布 \(\Big|\langle z_i\big|\psi(\boldsymbol\theta)\rangle\Big|^2\;\forall i\) からサンプルの最終セットを生成し、答えを取得します。
全体を通して多くのパラメーターがあり、特に試行波動関数の選択があります。 以下では、次を検討します。
ここで、 \(U_\mathrm{entangler}\) は制御位相ゲート(完全にエンタングルしたゲート)の集合であり、 \(U_\mathrm{single}(\theta) = \prod_{i=1}^N Y(\theta_{i})\) です。ここで、 \(N\) は量子ビットの数、 \(m\) は量子回路の深さです。
イジング・ハミルトニアンの構築#
\(VRP\) から、 \(K=n-1\) の場合を考慮することによってのみ、等式制約を使用してバイナリ多項式最適化を構築できます。 これらの場合、サブツアー除去制約は必要なく、問題は変数 \({\bf z}\) にのみあります。 特に、拡張ラグランジアンは次のように書くことができます。
ここで、 \(A\) は十分に大きいパラメーターです。
ハミルトニアンからQP定式化へ#
ベクトル \({\bf z}\) で、完全グラフ( \(\delta(i)^+ = \delta(i)^- = \{0,1,\dots,i-1,i+1,\dots,n\}\) )の場合、 \(H\) は次のように記述できます。
つまり:
ここで:最初の項は次の通りです:
第二の項は次の通りです:
第三の項は次の通りです:
イジング・ハミルトニアンのQP定式化はVQEの使用の準備ができています。 Qiskit optimizationで利用可能な最適化スタックを使用してQPを解決します。
参考文献#
[1] E. Farhi, J. Goldstone, S. Gutmann e-print arXiv 1411.4028, 2014
[2] Max-Cut and Traveling Salesman Problem
[3] C. E. Miller, E. W. Tucker, and R. A. Zemlin (1960). 「Integer Programming Formulations and Travelling Salesman Problems」. J. ACM. 7: 326–329. doi:10.1145/321043.321046.
[4] D. L. Applegate, R. M. Bixby, V. Chvátal, and W. J. Cook (2006). The Traveling Salesman Problem. Princeton University Press, ISBN 978-0-691-12993-8.
初期化#
まず、必要なパッケージをすべてロードします。CPLEXは古典計算に必要です。 pip install 'qiskit-optimization[cplex] ' でインストールできます。
[1]:
import numpy as np
import matplotlib.pyplot as plt
try:
import cplex
from cplex.exceptions import CplexError
except:
print("Warning: Cplex not found.")
import math
from qiskit_algorithms.utils import algorithm_globals
from qiskit_algorithms import SamplingVQE
from qiskit_algorithms.optimizers import SPSA
from qiskit.circuit.library import RealAmplitudes
from qiskit.primitives import Sampler
次に、変数を初期化します
[2]:
# Initialize the problem by defining the parameters
n = 3 # number of nodes + depot (n+1)
K = 2 # number of vehicles
ノードを2次元平面にランダムに配置し、ノード間の距離を計算する初期化クラスを定義します。
[3]:
# Get the data
class Initializer:
def __init__(self, n):
self.n = n
def generate_instance(self):
n = self.n
# np.random.seed(33)
np.random.seed(1543)
xc = (np.random.rand(n) - 0.5) * 10
yc = (np.random.rand(n) - 0.5) * 10
instance = np.zeros([n, n])
for ii in range(0, n):
for jj in range(ii + 1, n):
instance[ii, jj] = (xc[ii] - xc[jj]) ** 2 + (yc[ii] - yc[jj]) ** 2
instance[jj, ii] = instance[ii, jj]
return xc, yc, instance
[4]:
# Initialize the problem by randomly generating the instance
initializer = Initializer(n)
xc, yc, instance = initializer.generate_instance()
IBM ILOG CPLEXを使用した古典的なソリューション#
古典的なソリューションでは、IBM ILOGCPLEX を使用します。 CPLEX は、この問題の正確な解決策を見つけることができます。 まず、CPLEX が解決できる方法で問題をエンコードする ClassicalOptimizer クラスを定義し、次にクラスをインスタンス化して解決します。
[5]:
class ClassicalOptimizer:
def __init__(self, instance, n, K):
self.instance = instance
self.n = n # number of nodes
self.K = K # number of vehicles
def compute_allowed_combinations(self):
f = math.factorial
return f(self.n) / f(self.K) / f(self.n - self.K)
def cplex_solution(self):
# refactoring
instance = self.instance
n = self.n
K = self.K
my_obj = list(instance.reshape(1, n**2)[0]) + [0.0 for x in range(0, n - 1)]
my_ub = [1 for x in range(0, n**2 + n - 1)]
my_lb = [0 for x in range(0, n**2)] + [0.1 for x in range(0, n - 1)]
my_ctype = "".join(["I" for x in range(0, n**2)]) + "".join(
["C" for x in range(0, n - 1)]
)
my_rhs = (
2 * ([K] + [1 for x in range(0, n - 1)])
+ [1 - 0.1 for x in range(0, (n - 1) ** 2 - (n - 1))]
+ [0 for x in range(0, n)]
)
my_sense = (
"".join(["E" for x in range(0, 2 * n)])
+ "".join(["L" for x in range(0, (n - 1) ** 2 - (n - 1))])
+ "".join(["E" for x in range(0, n)])
)
try:
my_prob = cplex.Cplex()
self.populatebyrow(my_prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs)
my_prob.solve()
except CplexError as exc:
print(exc)
return
x = my_prob.solution.get_values()
x = np.array(x)
cost = my_prob.solution.get_objective_value()
return x, cost
def populatebyrow(self, prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs):
n = self.n
prob.objective.set_sense(prob.objective.sense.minimize)
prob.variables.add(obj=my_obj, lb=my_lb, ub=my_ub, types=my_ctype)
prob.set_log_stream(None)
prob.set_error_stream(None)
prob.set_warning_stream(None)
prob.set_results_stream(None)
rows = []
for ii in range(0, n):
col = [x for x in range(0 + n * ii, n + n * ii)]
coef = [1 for x in range(0, n)]
rows.append([col, coef])
for ii in range(0, n):
col = [x for x in range(0 + ii, n**2, n)]
coef = [1 for x in range(0, n)]
rows.append([col, coef])
# Sub-tour elimination constraints:
for ii in range(0, n):
for jj in range(0, n):
if (ii != jj) and (ii * jj > 0):
col = [ii + (jj * n), n**2 + ii - 1, n**2 + jj - 1]
coef = [1, 1, -1]
rows.append([col, coef])
for ii in range(0, n):
col = [(ii) * (n + 1)]
coef = [1]
rows.append([col, coef])
prob.linear_constraints.add(lin_expr=rows, senses=my_sense, rhs=my_rhs)
[6]:
# Instantiate the classical optimizer class
classical_optimizer = ClassicalOptimizer(instance, n, K)
# Print number of feasible solutions
print("Number of feasible solutions = " + str(classical_optimizer.compute_allowed_combinations()))
Number of feasible solutions = 3.0
[7]:
# Solve the problem in a classical fashion via CPLEX
x = None
z = None
try:
x, classical_cost = classical_optimizer.cplex_solution()
# Put the solution in the z variable
z = [x[ii] for ii in range(n**2) if ii // n != ii % n]
# Print the solution
print(z)
except:
print("CPLEX may be missing.")
[1.0, 1.0, 1.0, 0.0, 1.0, 0.0]
[8]:
# Visualize the solution
def visualize_solution(xc, yc, x, C, n, K, title_str):
plt.figure()
plt.scatter(xc, yc, s=200)
for i in range(len(xc)):
plt.annotate(i, (xc[i] + 0.15, yc[i]), size=16, color="r")
plt.plot(xc[0], yc[0], "r*", ms=20)
plt.grid()
for ii in range(0, n**2):
if x[ii] > 0:
ix = ii // n
iy = ii % n
plt.arrow(
xc[ix],
yc[ix],
xc[iy] - xc[ix],
yc[iy] - yc[ix],
length_includes_head=True,
head_width=0.25,
)
plt.title(title_str + " cost = " + str(int(C * 100) / 100.0))
plt.show()
if x is not None:
visualize_solution(xc, yc, x, classical_cost, n, K, "Classical")
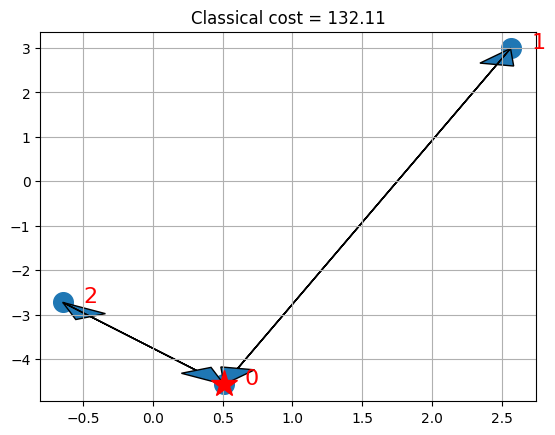
CPLEXを使用している場合、ソリューションは星付きのデポと矢印付きの車両に選択されたルートが表示されます。
ゼロからの量子ソリューション#
量子ソリューションには、Qiskitを使用します。
まず、問題を解決するために量子アプローチをエンコードするクラス QuantumOptimizer を使用して、ゼロからソリューションを導き出し、次にそれをインスタンス化して解決します。 クラス内で次のメソッドを定義します。
binary_representation:問題 \((M)\) をQP項(基本的に線形代数)にエンコードします。construct_problem:QuadraticProgramのインスタンスとしてQUBO最適化問題を構築します。solve_problem:デフォルトのパラメーターでSamplingVQEを使用することにより、MinimunEigenOptimizerを介して前のステップで構築された問題 \((M)\) を解決します。
[9]:
from qiskit_optimization import QuadraticProgram
from qiskit_optimization.algorithms import MinimumEigenOptimizer
class QuantumOptimizer:
def __init__(self, instance, n, K):
self.instance = instance
self.n = n
self.K = K
def binary_representation(self, x_sol=0):
instance = self.instance
n = self.n
K = self.K
A = np.max(instance) * 100 # A parameter of cost function
# Determine the weights w
instance_vec = instance.reshape(n**2)
w_list = [instance_vec[x] for x in range(n**2) if instance_vec[x] > 0]
w = np.zeros(n * (n - 1))
for ii in range(len(w_list)):
w[ii] = w_list[ii]
# Some variables I will use
Id_n = np.eye(n)
Im_n_1 = np.ones([n - 1, n - 1])
Iv_n_1 = np.ones(n)
Iv_n_1[0] = 0
Iv_n = np.ones(n - 1)
neg_Iv_n_1 = np.ones(n) - Iv_n_1
v = np.zeros([n, n * (n - 1)])
for ii in range(n):
count = ii - 1
for jj in range(n * (n - 1)):
if jj // (n - 1) == ii:
count = ii
if jj // (n - 1) != ii and jj % (n - 1) == count:
v[ii][jj] = 1.0
vn = np.sum(v[1:], axis=0)
# Q defines the interactions between variables
Q = A * (np.kron(Id_n, Im_n_1) + np.dot(v.T, v))
# g defines the contribution from the individual variables
g = (
w
- 2 * A * (np.kron(Iv_n_1, Iv_n) + vn.T)
- 2 * A * K * (np.kron(neg_Iv_n_1, Iv_n) + v[0].T)
)
# c is the constant offset
c = 2 * A * (n - 1) + 2 * A * (K**2)
try:
max(x_sol)
# Evaluates the cost distance from a binary representation of a path
fun = (
lambda x: np.dot(np.around(x), np.dot(Q, np.around(x)))
+ np.dot(g, np.around(x))
+ c
)
cost = fun(x_sol)
except:
cost = 0
return Q, g, c, cost
def construct_problem(self, Q, g, c) -> QuadraticProgram:
qp = QuadraticProgram()
for i in range(n * (n - 1)):
qp.binary_var(str(i))
qp.objective.quadratic = Q
qp.objective.linear = g
qp.objective.constant = c
return qp
def solve_problem(self, qp):
algorithm_globals.random_seed = 10598
vqe = SamplingVQE(sampler=Sampler(), optimizer=SPSA(), ansatz=RealAmplitudes())
optimizer = MinimumEigenOptimizer(min_eigen_solver=vqe)
result = optimizer.solve(qp)
# compute cost of the obtained result
_, _, _, level = self.binary_representation(x_sol=result.x)
return result.x, level
ステップ 1#
パラメーターを使用して量子オプティマイザークラスをインスタンス化します。
インスタンス。
ノードと車両の数
nとK。
[10]:
# Instantiate the quantum optimizer class with parameters:
quantum_optimizer = QuantumOptimizer(instance, n, K)
ステップ2#
問題をバイナリー形式(IH-QP)としてエンコードします。
整合性チェック: quantum optimizer 内のバイナリー定式化が正しいことを確認してください (つまり、同じ解で同じコストが得られることを確認します)。
[11]:
# Check if the binary representation is correct
try:
if z is not None:
Q, g, c, binary_cost = quantum_optimizer.binary_representation(x_sol=z)
print("Binary cost:", binary_cost, "classical cost:", classical_cost)
if np.abs(binary_cost - classical_cost) < 0.01:
print("Binary formulation is correct")
else:
print("Error in the binary formulation")
else:
print("Could not verify the correctness, due to CPLEX solution being unavailable.")
Q, g, c, binary_cost = quantum_optimizer.binary_representation()
print("Binary cost:", binary_cost)
except NameError as e:
print("Warning: Please run the cells above first.")
print(e)
Binary cost: 132.11148115684045 classical cost: 132.1114811568365
Binary formulation is correct
ステップ3#
QuadraticProgram のインスタンスとして問題をエンコードします。
[12]:
qp = quantum_optimizer.construct_problem(Q, g, c)
ステップ 4#
最適化スタックから MinimumEigenOptimizer を介して問題を解決します。 注意: 量子ビットの数によっては、状態ベクトル・シミュレーションに時間がかかる場合があります。 たとえば、12量子ビットの場合、12時間以上かかります。 ロギングは、プログラムが何をしているかを確認するのに役立ちます。
[13]:
quantum_solution, quantum_cost = quantum_optimizer.solve_problem(qp)
print(quantum_solution, quantum_cost)
[1. 1. 1. 0. 1. 0.] 132.11148115684045
ステップ5#
ソリューションの視覚化
[14]:
# Put the solution in a way that is compatible with the classical variables
x_quantum = np.zeros(n**2)
kk = 0
for ii in range(n**2):
if ii // n != ii % n:
x_quantum[ii] = quantum_solution[kk]
kk += 1
# visualize the solution
visualize_solution(xc, yc, x_quantum, quantum_cost, n, K, "Quantum")
# and visualize the classical for comparison
if x is not None:
visualize_solution(xc, yc, x, classical_cost, n, K, "Classical")
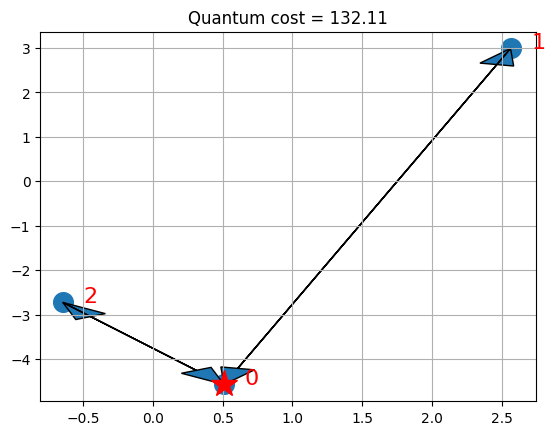
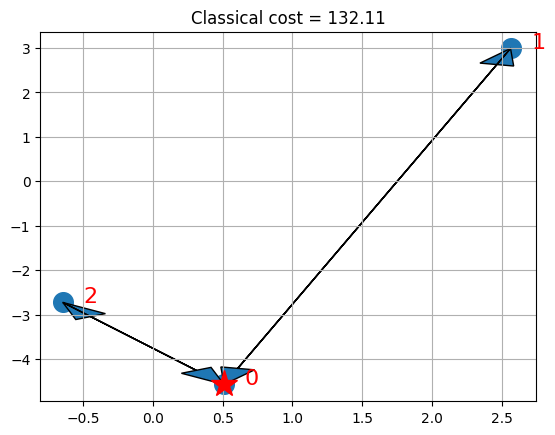
プロットには、デポに星が表示され、車両用に選択されたルートが矢印で表示されます。 この特定のケースでは、QP定式化の最適解を見つけることができます。これはたまたまILPの最適解と一致します。
ただし、VQEはイジングハミルトニアンのQP定式化にヒューリスティックに取り組んでいることに注意してください。 Aの適切な選択については、QP定式化の局所最適点がILPの実行可能解になります。 上記のような小さな例では、ILPの最適化と一致するQP定式化の最適解を見つけることができますが、ILPの最適解を見つけることは、QP定式化の局所最適を見つけることよりも困難で、一般的にILP実現可能な解を見つけるよりも難しいです。 VQE内でも、特定の変分形式(試行波動関数)に対してより強力な保証を提供する場合があります。
[15]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.23.0 |
qiskit-aer | 0.11.1 |
qiskit-optimization | 0.5.0 |
qiskit-machine-learning | 0.6.0 |
| System information | |
| Python version | 3.9.15 |
| Python compiler | Clang 14.0.0 (clang-1400.0.29.102) |
| Python build | main, Oct 11 2022 22:27:25 |
| OS | Darwin |
| CPUs | 4 |
| Memory (Gb) | 16.0 |
| Tue Dec 06 21:53:30 2022 JST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2022.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: