注釈

このページは docs/tutorials/04_grover_optimizer.ipynb から生成されました。

グローバーオプティマイザー#

はじめに#

グローバー適応探索（Grover Adaptive Search、GAS）は、変分量子固有ソルバー（Variational Quantum Eigensolver、VQE）や量子近似最適化アルゴリズム（Quantum Approximate Optimization Algorithm、QAOA）などの変分アルゴリズムとともに、組み合わせ最適化問題における可能な解決策として検討されてきました。アルゴリズムは、グローバー検索を繰り返し適用し、直前の実行までで最もよいと思われる値をしきい値として使用して、目的関数の最適値を見つけます。GASで使用されるアダプティブオラクルは、現在のしきい値より上または下のすべての値（それぞれ最大および最小）を認識し、最適値が見つかるまで、しきい値が更新されるたびに検索スペースのサイズを縮小します。

このノートブックでは、 [1] に記載されているように、制約なし二値変数二次計画問題(QUBO)を最小化することで、GASで記述されている手法を活用した GroverOptimizer の各コンポーネントを探索します。

参考文献#

[1] A. Gilliam, S. Woerner, C. Gonciulea, Grover Adaptive Search for Constrained Polynomial Binary Optimization, arXiv preprint arXiv:1912.04088 (2019).

グローバー適応探索#

GASのコア要素であるグローバー探索には、3つの材料が必要です:

探索スペース内の全ての状態を重ね合わせるための状態準備演算子 $A$ 。
関心のある状態を認識し、その振幅を-1で乗算するオラクル演算子 $O$ 。
$| 0 ⟩_{n}$ 状態の振幅に -1 を掛けるグローバー拡散演算子 $D$ 。

GASの実装は特定のユースケースによって異なりますが、一般的なフレームワークは、以下で説明する手順に大まかに従います。

9949090904c9417da6ceff9b27971fb7

GroverOptimizer は QuadraticProgramToNegativeValueOracle を使用して $A_{y}$ を構築し、 $n$ -qubitレジスタを準備し、 $| x ⟩_{n}$ と $m$ -qubitレジスタは対応する $| Q (x) - y ⟩_{m}$ を表します。次に、 $(Q (x) - y)$ の負のすべての状態に $O_{y}$ のフラグが付けられます。実装では、オラクル演算子は $y$ から独立していますが、これは必須ではありません。明確にするために、オラクルが $y$ から独立している場合は、オラクルを $O$ として参照します。

正式に言えば、 QuadraticProgramToNegativeValueOracle は、次のような $A_{y}$ と $O$ を構成します。

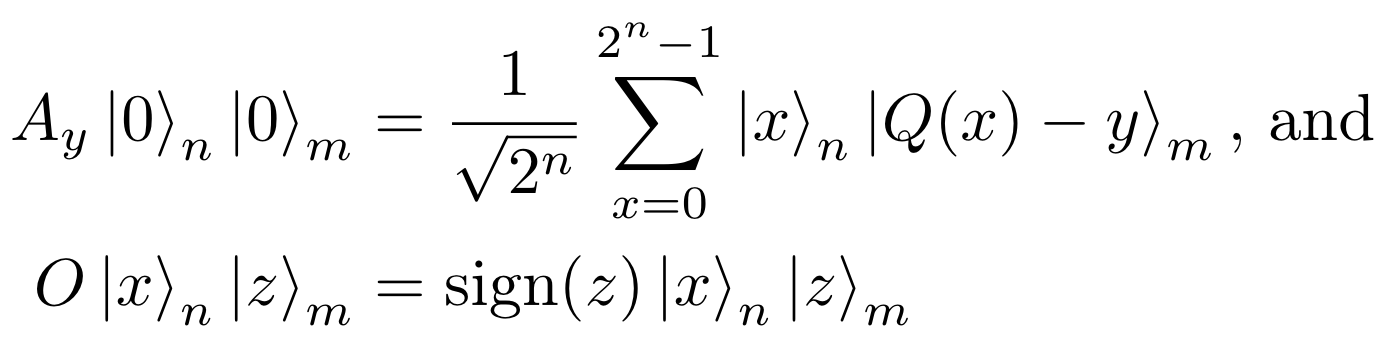
a5840348a8714c9191f0bddc83a688f9

ここで、 $| x ⟩$ は整数 $x$ のバイナリーエンコーディングです。

閾値 $y$ が更新される毎に、関数値が（それぞれ最小値と最大値に対して）上または下に $y$ だけシフトするように $A_{y}$ を適応させます。たとえば、最小値を見つけるコンテキストでは、 $y$ の値が減少すると、最小値のみが残るまで、探索空間（負の値）も減少します。具体的な例については、次のセクションで説明します。

GroverOptimizerを使用してQUBO問題の最小値を見つける#

以下は最小化問題のおもちゃの例です。

$\begin{array}{r} min_{x \in {0, 1}^{3}} - 2 x_{0} x_{2} - x_{1} x_{2} - 1 x_{0} + 2 x_{1} - 3 x_{2} . \end{array}$

最初のステップでは、上記の問題を定義するdocplexモデルを作成します。そして、from_docplex_mp() 関数を使用してモデルを QuadraticProgram に変換し、Qiskit Optimization で QUBO を表すために使用できます。

[1]:

from qiskit_algorithms import NumPyMinimumEigensolver
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import GroverOptimizer, MinimumEigenOptimizer
from qiskit_optimization.translators import from_docplex_mp
from docplex.mp.model import Model

[2]:

model = Model()
x0 = model.binary_var(name="x0")
x1 = model.binary_var(name="x1")
x2 = model.binary_var(name="x2")
model.minimize(-x0 + 2 * x1 - 3 * x2 - 2 * x0 * x2 - 1 * x1 * x2)
qp = from_docplex_mp(model)
print(qp.prettyprint())

Problem name: docplex_model1

Minimize
  -2*x0*x2 - x1*x2 - x0 + 2*x1 - 3*x2

Subject to
  No constraints

  Binary variables (3)
    x0 x1 x2

次に、6 量子ビットで値をエンコードする GroverOptimizer を作成します。そして、進行なしでGASが10回繰り返された後に終了します(すなわち、 $y$ の値は変化しません)。 solve() 関数は先ほど作成した QuadraticProgram を受け取り、実行に関する情報を含む結果オブジェクトを返します。

[3]:

grover_optimizer = GroverOptimizer(6, num_iterations=10, sampler=Sampler())
results = grover_optimizer.solve(qp)
print(results.prettyprint())

objective function value: -6.0
variable values: x0=1.0, x1=0.0, x2=1.0
status: SUCCESS

この結果、最適解 $x_{0} = 1$ 、 $x_{1} = 0$ 、 $x_{2} = 1$ が得られ、最適目的値は $- 6$ となります（ほとんどの時間は、ランダム化されたアルゴリズムによる）。以下の例では、量子状態のカスタム可視化は、このQUBOに適用される GroverOptimizer の実行可能性が示されています。

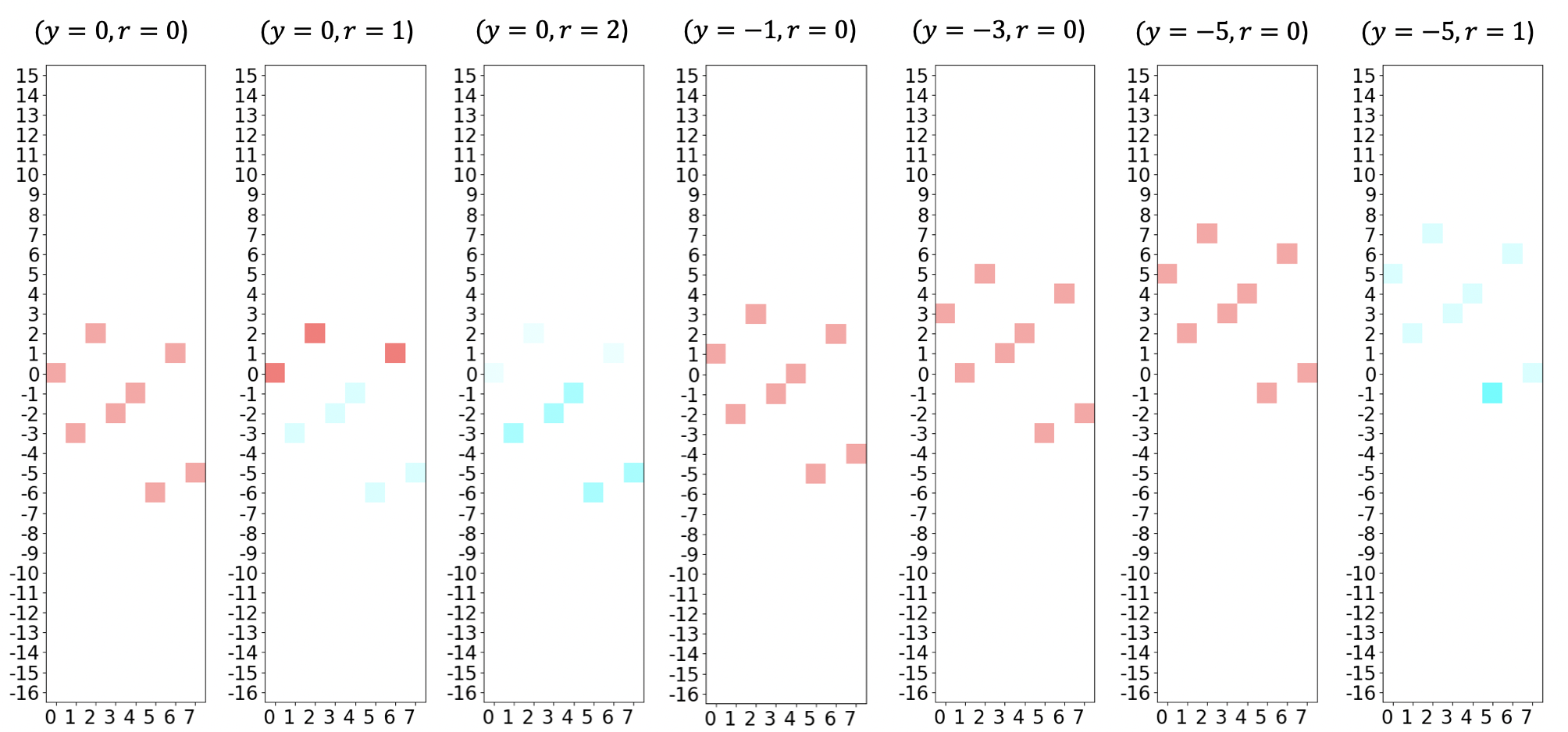
4c75b032b3384d2e8aa933756aa17af1

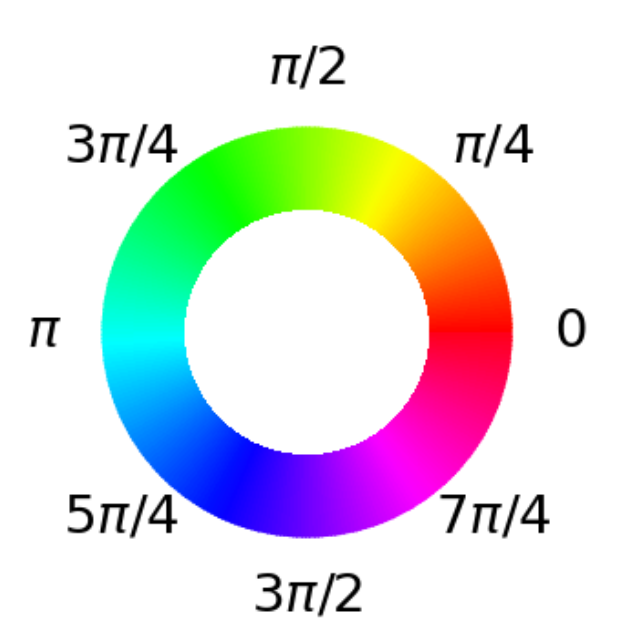
各グラフはGASの単一の反復を示しており、 $r$ （＝反復カウンター）と $y$ （＝しきい値/オフセット）の現在の値がタイトルに示されています。X軸は入力に相当する整数（例：『101』 $\to$ 5）を表示し、Y軸は可能な関数値を表示します。3つのバイナリ変数があるため、 $2^{3} = 8$ の可能な解決策があり、各グラフに示されています。色の強度は特定の結果を測定する確率を示し（明るい強度が最も高い）、実際の色は対応するフェーズを示します（以下のフェーズのカラーホイールを参照）。 $y$ が減少すると、すべての値がその量だけ上にシフトすることに注意してください。つまり、1つだけが残る（最小）まで、分布内の負の値はますます少なくなります。

a4d36019bd6c49388e55939642ec0a63

GroverOptimizerが正しい値を見つけることの確認#

Qiskit optimizationの MinimumEigenOptimizer を使用してアルゴリズムが正しく動作していることを確認できます。

[4]:

exact_solver = MinimumEigenOptimizer(NumPyMinimumEigensolver())
exact_result = exact_solver.solve(qp)
print(exact_result.prettyprint())

objective function value: -6.0
variable values: x0=1.0, x1=0.0, x2=1.0
status: SUCCESS

[5]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
`qiskit-terra`	0.23.0
`qiskit-aer`	0.11.1
`qiskit-optimization`	0.5.0
`qiskit-machine-learning`	0.6.0
System information
Python version	3.9.15
Python compiler	Clang 14.0.0 (clang-1400.0.29.102)
Python build	main, Oct 11 2022 22:27:25
OS	Darwin
CPUs	4
Memory (Gb)	16.0
Tue Dec 06 21:47:01 2022 JST

This code is a part of Qiskit

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.

[ ]: