Nota
Esta página fue generada a partir de docs/tutorials/03_minimum_eigen_optimizer.ipynb.
Optimizador Propio Mínimo#
Introducción#
Una clase interesante de problemas de optimización que debe abordar la computación cuántica son los problemas de Optimización Binaria Cuadrática sin Restricciones (Quadratic Unconstrained Binary Optimization, QUBO). Encontrar la solución a un QUBO es equivalente a encontrar el estado fundamental de un Hamiltoniano de Ising correspondiente, que es un problema importante no solo en la optimización, sino también en química cuántica y física. Para esta traducción, las variables binarias que toman valores en \(\{0, 1\}\) se reemplazan por variables de espín que toman valores en \(\{-1, +1\}\), lo que permite reemplazar las variables de espín resultantes por matrices Pauli Z y, por lo tanto, un Hamiltoniano de Ising. Para más detalles sobre este mapeo nos referimos a [1].
Qiskit Optimization proporciona conversión automática de un QuadraticProgram adecuado a un Hamiltoniano de Ising, que luego permite aprovechar todas las implementaciones de SamplingMinimumEigensolver, como
SamplingVQE,QAOA, oNumpyMinimumEigensolver(método clásico exacto).
Nota 1: MinimumEigenOptimizer no es compatible con qiskit_algorithms.VQE. Pero en su lugar se puede usar qiskit_algorithms.SamplingVQE.
Nota 2: MinimumEigenOptimizer puede usar NumpyMinimumEigensolver como un caso de excepción, aunque hereda de MinimumEigensolver (no de SamplingMinimumEigensolver).
Qiskit Optimization proporciona una clase MinimumEigenOptimizer, que envuelve la traducción a un Hamiltoniano de Ising (en Qiskit Terra también llamado SparsePauliOp), la llamada a un MinimumEigensolver y la traducción de los resultados de vuelta a un OptimizationResult.
A continuación, primero ilustramos la conversión de un QuadraticProgram a un SparsePauliOp y luego mostramos cómo usar el MinimumEigenOptimizer con diferentes MinimumEigensolvers para resolver un QuadraticProgram dado. Los algoritmos en Qiskit Optimization intentan convertir automáticamente un problema determinado a la clase de problema soportada si es posible, por ejemplo, el MinimumEigenOptimizer traducirá automáticamente las variables enteras a variables binarias o agregará restricciones de igualdad lineal como un término de penalización cuadrática al objetivo. Se debe mencionar que se generará un QiskitOptimizationError si se intenta la conversión de un programa cuadrático con variables enteras.
La profundidad del circuito de QAOA podría ser incrementada con el tamaño del problema, lo que podría ser prohibitivo para los dispositivos cuánticos a corto plazo. Un posible método alternativo es el QAOA recursivo, como se introduce en la referencia [2]. Qiskit Optimization generaliza este concepto a RecursiveMinimumEigenOptimizer, el cual se introduce al final de este tutorial.
Referencias#
[1] A. Lucas, Ising formulations of many NP problems, Front. Phys., 12 (2014).
Convertir un QUBO a un SparsePauliOp#
[1]:
from qiskit_algorithms.utils import algorithm_globals
from qiskit_algorithms import QAOA, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import COBYLA
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import (
MinimumEigenOptimizer,
RecursiveMinimumEigenOptimizer,
SolutionSample,
OptimizationResultStatus,
)
from qiskit_optimization import QuadraticProgram
from qiskit.visualization import plot_histogram
from typing import List, Tuple
import numpy as np
[2]:
# create a QUBO
qubo = QuadraticProgram()
qubo.binary_var("x")
qubo.binary_var("y")
qubo.binary_var("z")
qubo.minimize(linear=[1, -2, 3], quadratic={("x", "y"): 1, ("x", "z"): -1, ("y", "z"): 2})
print(qubo.prettyprint())
Problem name:
Minimize
x*y - x*z + 2*y*z + x - 2*y + 3*z
Subject to
No constraints
Binary variables (3)
x y z
A continuación traducimos este QUBO en un operador de Ising. Esto no solo resulta en un SparsePauliOp, sino también en un desplazamiento constante que se debe tener en cuenta para cambiar el valor resultante.
[3]:
op, offset = qubo.to_ising()
print("offset: {}".format(offset))
print("operator:")
print(op)
offset: 1.5
operator:
SparsePauliOp(['IIZ', 'IZI', 'ZII', 'IZZ', 'ZIZ', 'ZZI'],
coeffs=[-0.5 +0.j, 0.25+0.j, -1.75+0.j, 0.25+0.j, -0.25+0.j, 0.5 +0.j])
A veces, un QuadraticProgram también podría ser dado directamente en forma de SparsePauliOp. Para tales casos, Qiskit Optimization también proporciona un traductor de un SparsePauliOp de vuelta a un QuadraticProgram, que ilustramos a continuación.
[4]:
qp = QuadraticProgram()
qp.from_ising(op, offset, linear=True)
print(qp.prettyprint())
Problem name:
Minimize
x0*x1 - x0*x2 + 2*x1*x2 + x0 - 2*x1 + 3*x2
Subject to
No constraints
Binary variables (3)
x0 x1 x2
Este traductor permite, por ejemplo, traducir un SparsePauliOp a un QuadraticProgram y luego resolver el problema con otros algoritmos que no se basan en la representación del Hamiltoniano de Ising, como el GroverOptimizer.
Resolver un QUBO con el MinimumEigenOptimizer#
Empezamos inicializando el MinimumEigensolver que queremos usar.
[5]:
algorithm_globals.random_seed = 10598
qaoa_mes = QAOA(sampler=Sampler(), optimizer=COBYLA(), initial_point=[0.0, 0.0])
exact_mes = NumPyMinimumEigensolver()
Luego, usamos el MinimumEigensolver para crear un MinimumEigenOptimizer.
[6]:
qaoa = MinimumEigenOptimizer(qaoa_mes) # using QAOA
exact = MinimumEigenOptimizer(exact_mes) # using the exact classical numpy minimum eigen solver
Primero usamos el MinimumEigenOptimizer basado en el NumPyMinimumEigensolver exacto clásico para obtener la solución de referencia óptima para este pequeño ejemplo.
[7]:
exact_result = exact.solve(qubo)
print(exact_result.prettyprint())
objective function value: -2.0
variable values: x=0.0, y=1.0, z=0.0
status: SUCCESS
A continuación aplicamos el MinimumEigenOptimizer basado en QAOA al mismo problema.
[8]:
qaoa_result = qaoa.solve(qubo)
print(qaoa_result.prettyprint())
objective function value: -2.0
variable values: x=0.0, y=1.0, z=0.0
status: SUCCESS
Análisis de Muestras#
OptimizationResult proporciona información útil en forma de SolutionSamples (aquí indicado como muestras). Cada SolutionSample contiene información sobre los valores de entrada (x), el valor de la función objetivo correspondiente (fval), la fracción de muestras correspondiente a esa entrada (probability) y la solución status (SUCCESS, FAILURE, INFEASIBLE). Múltiples muestras correspondientes a la misma entrada se consolidan en una sola SolutionSample (siendo su atributo probability la fracción agregada de muestras representada por esa SolutionSample).
[9]:
print("variable order:", [var.name for var in qaoa_result.variables])
for s in qaoa_result.samples:
print(s)
variable order: ['x', 'y', 'z']
SolutionSample(x=array([0., 1., 0.]), fval=-2.0, probability=0.4409914383320322, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 0.]), fval=0.0, probability=0.2276808656506505, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 0.]), fval=0.0, probability=0.1413908468641879, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 0.]), fval=1.0, probability=0.1257339279014548, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 1.]), fval=3.0, probability=0.020491301242878, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 1.]), fval=3.0, probability=0.0304288193232328, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 1., 1.]), fval=3.0, probability=0.0123642766450843, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 1.]), fval=4.0, probability=0.0009185240404783, status=<OptimizationResultStatus.SUCCESS: 0>)
También es posible que deseemos filtrar muestras de acuerdo con su estado o probabilidades.
[10]:
def get_filtered_samples(
samples: List[SolutionSample],
threshold: float = 0,
allowed_status: Tuple[OptimizationResultStatus] = (OptimizationResultStatus.SUCCESS,),
):
res = []
for s in samples:
if s.status in allowed_status and s.probability > threshold:
res.append(s)
return res
[11]:
filtered_samples = get_filtered_samples(
qaoa_result.samples, threshold=0.005, allowed_status=(OptimizationResultStatus.SUCCESS,)
)
for s in filtered_samples:
print(s)
SolutionSample(x=array([0., 1., 0.]), fval=-2.0, probability=0.4409914383320322, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 0.]), fval=0.0, probability=0.2276808656506505, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 0.]), fval=0.0, probability=0.1413908468641879, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 0.]), fval=1.0, probability=0.1257339279014548, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 1.]), fval=3.0, probability=0.020491301242878, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 1.]), fval=3.0, probability=0.0304288193232328, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 1., 1.]), fval=3.0, probability=0.0123642766450843, status=<OptimizationResultStatus.SUCCESS: 0>)
Si queremos obtener una mejor perspectiva de los resultados, la estadística es de gran ayuda, tanto con respecto a los valores de la función objetivo como a sus respectivas probabilidades. Por lo tanto, la media y la desviación estándar son los elementos básicos para comprender los resultados.
[12]:
fvals = [s.fval for s in qaoa_result.samples]
probabilities = [s.probability for s in qaoa_result.samples]
[13]:
np.mean(fvals)
[13]:
1.5
[14]:
np.std(fvals)
[14]:
1.9364916731037085
Finalmente, a pesar de todo el procesamiento numérico, la visualización suele ser el mejor enfoque de análisis temprano.
[15]:
samples_for_plot = {
" ".join(f"{qaoa_result.variables[i].name}={int(v)}" for i, v in enumerate(s.x)): s.probability
for s in filtered_samples
}
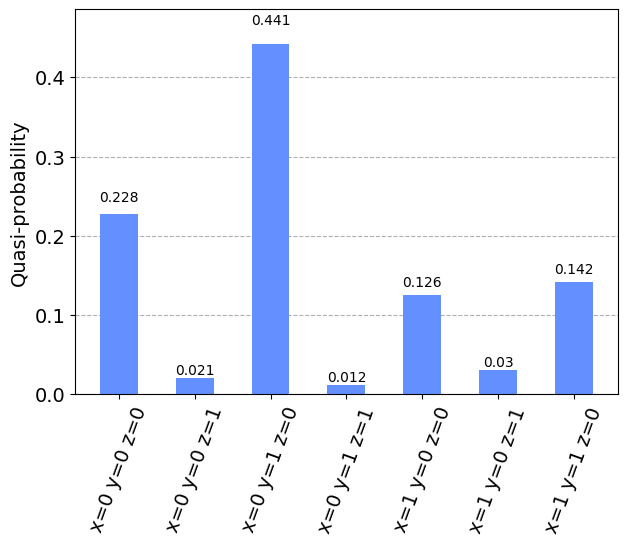
samples_for_plot
[15]:
{'x=0 y=1 z=0': 0.4409914383320322,
'x=0 y=0 z=0': 0.2276808656506505,
'x=1 y=1 z=0': 0.1413908468641879,
'x=1 y=0 z=0': 0.1257339279014548,
'x=0 y=0 z=1': 0.020491301242878,
'x=1 y=0 z=1': 0.0304288193232328,
'x=0 y=1 z=1': 0.0123642766450843}
[16]:
plot_histogram(samples_for_plot)
[16]:
RecursiveMinimumEigenOptimizer#
El RecursiveMinimumEigenOptimizer toma un MinimumEigenOptimizer como entrada y aplica el esquema de optimización recursiva para reducir el tamaño del problema una variable a la vez. Una vez que el tamaño del problema intermedio generado está por debajo de un umbral dado (min_num_vars), el RecursiveMinimumEigenOptimizer usa otro solucionador (min_num_vars_optimizer), por ejemplo, un solucionador clásico exacto como CPLEX o el MinimumEigenOptimizer basado en el NumPyMinimumEigensolver.
A continuación, mostramos cómo usar el RecursiveMinimumEigenOptimizer usando los dos MinimumEigenOptimizers presentados anteriormente.
En primer lugar, construimos el RecursiveMinimumEigenOptimizer tal que reduce el tamaño del problema de 3 variables a 1 variable y luego utiliza el solucionador exacto para la última variable. Entonces llamamos a solve para optimizar el problema considerado.
[17]:
rqaoa = RecursiveMinimumEigenOptimizer(qaoa, min_num_vars=1, min_num_vars_optimizer=exact)
[18]:
rqaoa_result = rqaoa.solve(qubo)
print(rqaoa_result.prettyprint())
objective function value: -2.0
variable values: x=0.0, y=1.0, z=0.0
status: SUCCESS
[19]:
filtered_samples = get_filtered_samples(
rqaoa_result.samples, threshold=0.005, allowed_status=(OptimizationResultStatus.SUCCESS,)
)
[20]:
samples_for_plot = {
" ".join(f"{rqaoa_result.variables[i].name}={int(v)}" for i, v in enumerate(s.x)): s.probability
for s in filtered_samples
}
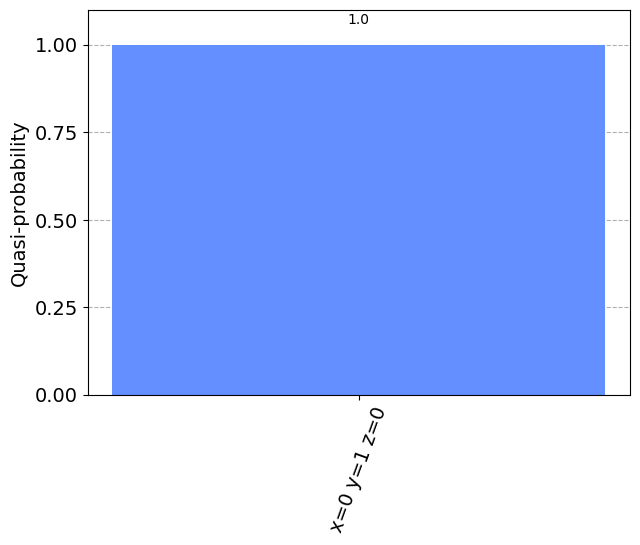
samples_for_plot
[20]:
{'x=0 y=1 z=0': 1.0}
[21]:
plot_histogram(samples_for_plot)
[21]:
[22]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.25.0.dev0+1d844ec |
qiskit-aer | 0.12.0 |
qiskit-ibmq-provider | 0.20.2 |
qiskit-nature | 0.7.0 |
qiskit-optimization | 0.6.0 |
| System information | |
| Python version | 3.10.11 |
| Python compiler | Clang 14.0.0 (clang-1400.0.29.202) |
| Python build | main, Apr 7 2023 07:31:31 |
| OS | Darwin |
| CPUs | 4 |
| Memory (Gb) | 16.0 |
| Thu May 18 16:56:50 2023 JST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: