Nota

Esta página fue generada a partir de docs/tutorials/11_quadratic_hamiltonian_and_slater_determinants.ipynb.

Hamiltonianos cuadráticos y determinantes de Slater#

Un Hamiltoniano cuadrático es un Hamiltoniano de la forma

\[H = \sum_{j, k} M_{jk} a^\dagger_j a_k + \frac12 \sum_{j, k} (\Delta_{jk} a^\dagger_j a^\dagger_k + \Delta^*_{jk} a_k a_j) + \text{constante}\]

donde \(M\) es una matrix Hermitiana (\(M^\dagger = M\)) y \(\Delta\) es una matriz antisimétrica (\(\Delta^T = -\Delta\)), y los \(\{a_j^\dagger\}\) son operadores de creación fermiónicos que satisfacen las relaciones de anticonmutación

\[\begin{split}\begin{align} a_j a_k + a_k a_j &= 0 \\ a_j a^\dagger_k + a^\dagger_k a_j &= \delta_{pq} \end{align}.\end{split}\]

Los Hamiltonianos cuadráticos son una clase importante de Hamiltonianos que son clásicamente tratables. Sus estados propios se denominan estados fermiónicos Gaussianos y se pueden preparar de manera eficiente en una computadora cuántica. Qiskit Nature incluye la clase QuadraticHamiltonian para representar Hamiltonianos cuadráticos.

Por supuesto, la clase FermionicOp también se puede utilizar para representar cualquier Hamiltoniano cuadrático. La razón para tener una clase específica para Hamiltonianos cuadráticos es que soporta rutinas numéricas especiales que implican realizar álgebra lineal en las matrices \(M\) y \(\Delta\). El formato de representación interna de FermionicOp no es adecuado para estas rutinas.

Un Hamiltoniano cuadrático se inicializa así:

[1]:

import numpy as np
from qiskit_nature.second_q.hamiltonians import QuadraticHamiltonian

# create Hamiltonian
hermitian_part = np.array(
    [
        [1.0, 2.0, 0.0, 0.0],
        [2.0, 1.0, 2.0, 0.0],
        [0.0, 2.0, 1.0, 2.0],
        [0.0, 0.0, 2.0, 1.0],
    ]
)
antisymmetric_part = np.array(
    [
        [0.0, 3.0, 0.0, 0.0],
        [-3.0, 0.0, 3.0, 0.0],
        [0.0, -3.0, 0.0, 3.0],
        [0.0, 0.0, -3.0, 0.0],
    ]
)
constant = 4.0

hamiltonian = QuadraticHamiltonian(
    hermitian_part=hermitian_part,
    antisymmetric_part=antisymmetric_part,
    constant=constant,
)

# convert it to a FermionicOp and print it
hamiltonian_ferm = hamiltonian.second_q_op()
print(hamiltonian_ferm)

Fermionic Operator
number spin orbitals=4, number terms=29
  4.0
+ 1.0 * ( +_0 -_0 )
+ 2.0 * ( +_0 -_1 )
+ 2.0 * ( +_1 -_0 )
+ 3.0 * ( +_0 +_1 )
+ 3.0 * ( -_1 -_0 )
+ 0.0 * ( +_0 -_2 )
+ 0.0 * ( +_2 -_0 )
+ 0.0 * ( +_0 +_2 )
+ 0.0 * ( -_2 -_0 )
+ 0.0 * ( +_0 -_3 )
+ 0.0 * ( +_3 -_0 )
+ 0.0 * ( +_0 +_3 )
+ 0.0 * ( -_3 -_0 )
+ 1.0 * ( +_1 -_1 )
+ 2.0 * ( +_1 -_2 )
+ 2.0 * ( +_2 -_1 )
+ 3.0 * ( +_1 +_2 )
+ 3.0 * ( -_2 -_1 )
+ 0.0 * ( +_1 -_3 )
+ 0.0 * ( +_3 -_1 )
+ 0.0 * ( +_1 +_3 )
+ 0.0 * ( -_3 -_1 )
+ 1.0 * ( +_2 -_2 )
+ 2.0 * ( +_2 -_3 )
+ 2.0 * ( +_3 -_2 )
+ 3.0 * ( +_2 +_3 )
+ 3.0 * ( -_3 -_2 )
+ 1.0 * ( +_3 -_3 )

Diagonalización y preparación de estado#

Un Hamiltoniano cuadrático siempre se puede reescribir en la forma

\[H = \sum_{j} \varepsilon_j b^\dagger_j b_j + \text{constante}\]

donde \(\varepsilon_0 \leq \varepsilon_1 \leq \cdots \leq \varepsilon_N\) son números reales no negativos llamados energías orbitales y los \(\{b_j^\dagger\}\) son un nuevo conjunto de operadores fermiónicos de creación que también satisfacen las relaciones canónicas de anticonmutación. Estos nuevos operadores de creación son combinaciones lineales de los operadores de creación y aniquilación originales:

\[\begin{split}\begin{pmatrix} b^\dagger_1 \\ \vdots \\ b^\dagger_N \\ \end{pmatrix} = W \begin{pmatrix} a^\dagger_1 \\ \vdots \\ a^\dagger_N \\ a_1 \\ \vdots \\ a_N \end{pmatrix},\end{split}\]

donde \(W\) es una matriz de \(N \times 2N\). Dada una base de vectores propios del Hamiltoniano, cada vector propio está etiquetado por un subconjunto de \(\{0, \ldots, N - 1\}\), que llamamos orbitales ocupados. El valor propio correspondiente es la suma de los valores correspondientes de \(\varepsilon_j\), más la constante.

[2]:

# get the transformation matrix W and orbital energies {epsilon_j}
(
    transformation_matrix,
    orbital_energies,
    transformed_constant,
) = hamiltonian.diagonalizing_bogoliubov_transform()

print(f"Shape of matrix W: {transformation_matrix.shape}")
print(f"Orbital energies: {orbital_energies}")
print(f"Transformed constant: {transformed_constant}")

Shape of matrix W: (4, 8)
Orbital energies: [0.29826763 4.38883678 5.5513683  5.64193745]
Transformed constant: -1.9402050758492795

La matriz de transformación \(W\) se utiliza para construir un circuito para preparar un vector propio del Hamiltoniano. El circuito se construye usando la clase FermionicGaussianState. Actualmente, solo se admite la Transformada de Jordan-Wigner. El circuito para la Transformada de Jordan-Wigner tiene una profundidad lineal y emplea únicamente conectividad lineal de qubits. El algoritmo es de Phys. Rev. Applied 9, 044036.

[3]:

from qiskit_nature.second_q.circuit.library import FermionicGaussianState

occupied_orbitals = (0, 2)
eig = np.sum(orbital_energies[list(occupied_orbitals)]) + transformed_constant
print(f"Eigenvalue: {eig}")

circuit = FermionicGaussianState(transformation_matrix, occupied_orbitals=occupied_orbitals)
circuit.draw("mpl")

Eigenvalue: 3.909430851761581

[3]:
../_images/tutorials_11_quadratic_hamiltonian_and_slater_determinants_5_1.png

La siguiente celda de código simula el circuito y verifica que el estado de salida sea de hecho un estado propio del Hamiltoniano con el valor propio esperado.

[4]:

from qiskit.quantum_info import Statevector
from qiskit_nature.second_q.mappers import JordanWignerMapper

# simulate the circuit to get the final state
state = np.array(Statevector(circuit))

# convert the Hamiltonian to a matrix
hamiltonian_jw = JordanWignerMapper().map(hamiltonian_ferm).to_matrix()

# check that the state is an eigenvector with the expected eigenvalue
np.testing.assert_allclose(hamiltonian_jw @ state, eig * state, atol=1e-8)

Determinantes de Slater#

Cuando la parte antisimétrica \(\Delta = 0\), entonces el Hamiltoniano conserva el número de partículas. En este caso, el cambio de base solo necesita mezclar operadores de creación, no operadores de aniquilación:

\[\begin{split}\begin{pmatrix} b^\dagger_1 \\ \vdots \\ b^\dagger_N \\ \end{pmatrix} = W \begin{pmatrix} a^\dagger_1 \\ \vdots \\ a^\dagger_N \\ \end{pmatrix},\end{split}\]

donde ahora \(W\) es una matriz de \(N \times N\). Además, las energías orbitales \(\{\varepsilon_j\}\) pueden ser negativas.

[5]:

# create Hamiltonian
hermitian_part = np.array(
    [
        [1.0, 2.0, 0.0, 0.0],
        [2.0, 1.0, 2.0, 0.0],
        [0.0, 2.0, 1.0, 2.0],
        [0.0, 0.0, 2.0, 1.0],
    ]
)
constant = 4.0

hamiltonian = QuadraticHamiltonian(
    hermitian_part=hermitian_part,
    constant=constant,
)

print(f"Hamiltonian conserves particle number: {hamiltonian.conserves_particle_number()}")

Hamiltonian conserves particle number: True

[6]:

# get the transformation matrix W and orbital energies {epsilon_j}
(
    transformation_matrix,
    orbital_energies,
    transformed_constant,
) = hamiltonian.diagonalizing_bogoliubov_transform()

print(f"Shape of matrix W: {transformation_matrix.shape}")
print(f"Orbital energies: {orbital_energies}")
print(f"Transformed constant: {transformed_constant}")

Shape of matrix W: (4, 4)
Orbital energies: [-2.23606798 -0.23606798  2.23606798  4.23606798]
Transformed constant: 4.0

En este caso especial, los estados propios se denominan determinantes de Slater y se usa un algoritmo más eficiente para prepararlos. Se accede a este algoritmo utilizando la clase SlaterDeterminant en lugar de FermionicGaussianState. SlaterDeterminant no toma los orbitales ocupados como entrada. En su lugar, se permite que varíe la forma de la matriz de transformación. Debería ser una matriz de \(\eta \times N\) donde \(\eta\) es el número de partículas.

[7]:

from qiskit_nature.second_q.circuit.library import SlaterDeterminant

occupied_orbitals = (0, 2)
eig = np.sum(orbital_energies[list(occupied_orbitals)]) + transformed_constant
print(f"Eigenvalue: {eig}")

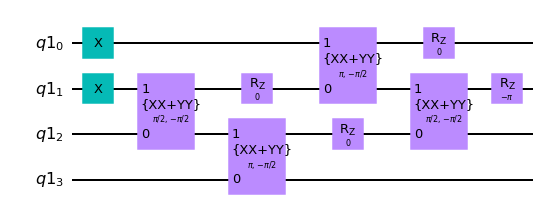
circuit = SlaterDeterminant(transformation_matrix[list(occupied_orbitals)])
circuit.draw("mpl")

Eigenvalue: 4.000000000000001

[7]:
../_images/tutorials_11_quadratic_hamiltonian_and_slater_determinants_12_1.png

Evolución temporal#

La evolución temporal bajo un Hamiltoniano cuadrático se puede realizar fácilmente cambiando a la base diagonal del Hamiltoniano. Los circuitos de preparación de estado que se muestran arriba efectúan este cambio de base, pero están optimizados para la preparación de estado a partir de un estado de base computacional (se supone que es el estado cero), y no funcionan en estados arbitrarios. El cambio de base unitaria general que funciona en estados arbitrarios se denomina transformada de Bogoliubov y también está implementada en Qiskit Nature.

El siguiente bloque de código demuestra el uso de la transformada de Bogoliubov para implementar la evolución temporal de un Hamiltoniano cuadrático.

[8]:

from qiskit_nature.second_q.circuit.library import BogoliubovTransform
from qiskit import QuantumCircuit, QuantumRegister
from qiskit.quantum_info import random_hermitian, random_statevector, state_fidelity
from scipy.linalg import expm

# create Hamiltonian
n_modes = 5
hermitian_part = np.array(random_hermitian(n_modes))
hamiltonian = QuadraticHamiltonian(hermitian_part=hermitian_part)

# diagonalize Hamiltonian
(
    transformation_matrix,
    orbital_energies,
    _,
) = hamiltonian.diagonalizing_bogoliubov_transform()

# set simulation time and construct time evolution circuit
time = 1.0
register = QuantumRegister(n_modes)
circuit = QuantumCircuit(register)
bog_circuit = BogoliubovTransform(transformation_matrix)
# change to the diagonal basis of the Hamiltonian
circuit.append(bog_circuit.inverse(), register)
# perform time evolution by applying z rotations
for q, energy in zip(register, orbital_energies):
    circuit.rz(-energy * time, q)
# change back to the original basis
circuit.append(bog_circuit, register)

# simulate the circuit
initial_state = random_statevector(2**n_modes)
final_state = initial_state.evolve(circuit)

# compute the correct state by direct exponentiation
hamiltonian_jw = JordanWignerMapper().map(hamiltonian.second_q_op()).to_matrix()
exact_evolution_op = expm(-1j * time * hamiltonian_jw)
expected_state = exact_evolution_op @ np.array(initial_state)

# check that the simulated state is correct
fidelity = state_fidelity(final_state, expected_state)
np.testing.assert_allclose(fidelity, 1.0, atol=1e-8)

[9]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit SoftwareVersion
qiskit-terra0.21.0.dev0+cbc801e
qiskit-aer0.11.0
qiskit-nature0.4.0
System information
Python version3.9.6
Python compilerGCC 8.5.0 20210514 (Red Hat 8.5.0-3)
Python builddefault, Aug 11 2021 06:39:25
OSLinux
CPUs4
Memory (Gb)15.314849853515625
Thu Jun 09 11:38:02 2022 EDT

This code is a part of Qiskit

© Copyright IBM 2017, 2022.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.