注釈
このページは、 docs/tutorials/11_quadratic_hamiltonian_and_slater_determinants.ipynb によって生成されたページです。
二次ハミルトニアンとスレーター行列式#
二次ハミルトニアンは、以下の形式のハミルトニアンです。
ここで、 \(M\) はエルミート行列( \(M^\dagger = M\) )、 \(\Delta\) は反対称行列( \(\Delta^T = -\Delta\) )であり、 \(\{a_j^\dagger\}\) は反交換関係を満たすフェルミオン生成演算子です。
二次ハミルトニアンは、古典的に扱いやすいハミルトニアンの重要なクラスです。それらの固有状態はフェルミオンガウス状態と呼ばれ、量子コンピューター上で効率的に作成することができます。Qiskit Natureには、2次ハミルトニアンを表すための QuadraticHamiltonian クラスが含まれています。
もちろん、 FermionicOp クラスは、任意の二次ハミルトニアンを表すために使用することもできます。二次ハミルトニアンに特化したクラスを持つ理由は、行列 \(M\) および \(\Delta\) 上で線形代数を実行することを含む特別な数値ルーチンをサポートすることです。 FermionicOp の内部表現形式は、これらのルーチンには適していません。
二次ハミルトニアンは次のように初期化されます。
[1]:
import numpy as np
from qiskit_nature.second_q.hamiltonians import QuadraticHamiltonian
# create Hamiltonian
hermitian_part = np.array(
[
[1.0, 2.0, 0.0, 0.0],
[2.0, 1.0, 2.0, 0.0],
[0.0, 2.0, 1.0, 2.0],
[0.0, 0.0, 2.0, 1.0],
]
)
antisymmetric_part = np.array(
[
[0.0, 3.0, 0.0, 0.0],
[-3.0, 0.0, 3.0, 0.0],
[0.0, -3.0, 0.0, 3.0],
[0.0, 0.0, -3.0, 0.0],
]
)
constant = 4.0
hamiltonian = QuadraticHamiltonian(
hermitian_part=hermitian_part,
antisymmetric_part=antisymmetric_part,
constant=constant,
)
# convert it to a FermionicOp and print it
hamiltonian_ferm = hamiltonian.second_q_op()
print(hamiltonian_ferm)
Fermionic Operator
number spin orbitals=4, number terms=29
4.0
+ 1.0 * ( +_0 -_0 )
+ 2.0 * ( +_0 -_1 )
+ 2.0 * ( +_1 -_0 )
+ 3.0 * ( +_0 +_1 )
+ 3.0 * ( -_1 -_0 )
+ 0.0 * ( +_0 -_2 )
+ 0.0 * ( +_2 -_0 )
+ 0.0 * ( +_0 +_2 )
+ 0.0 * ( -_2 -_0 )
+ 0.0 * ( +_0 -_3 )
+ 0.0 * ( +_3 -_0 )
+ 0.0 * ( +_0 +_3 )
+ 0.0 * ( -_3 -_0 )
+ 1.0 * ( +_1 -_1 )
+ 2.0 * ( +_1 -_2 )
+ 2.0 * ( +_2 -_1 )
+ 3.0 * ( +_1 +_2 )
+ 3.0 * ( -_2 -_1 )
+ 0.0 * ( +_1 -_3 )
+ 0.0 * ( +_3 -_1 )
+ 0.0 * ( +_1 +_3 )
+ 0.0 * ( -_3 -_1 )
+ 1.0 * ( +_2 -_2 )
+ 2.0 * ( +_2 -_3 )
+ 2.0 * ( +_3 -_2 )
+ 3.0 * ( +_2 +_3 )
+ 3.0 * ( -_3 -_2 )
+ 1.0 * ( +_3 -_3 )
対角化と状態の準備#
二次ハミルトニアンは常に以下の形式で書き換えることができます。
ここで、 \(\varepsilon_0 \leq \varepsilon_1 \leq \cdots \leq \varepsilon_N\) は軌道エネルギーと呼ばれる非負の実数であり、 \(\{b_j^\dagger\}\) は正規の反交換関係も満たすフェルミ粒子生成演算子の新しいセットです。これらの新しい生成演算子は、元の生成演算子と消滅演算子の線形結合です。
ここで、 \(W\) は \(N \times 2N\) 行列です。ハミルトニアンの固有ベクトルの基底を考えると、各固有ベクトルは、占有軌道と呼ばれる \(\{0, \ldots, N - 1\}\) のサブセットによってラベル付けされます。 対応する固有値は、 \(\varepsilon_j\) の対応する値の合計に定数を加えたものです。
[2]:
# get the transformation matrix W and orbital energies {epsilon_j}
(
transformation_matrix,
orbital_energies,
transformed_constant,
) = hamiltonian.diagonalizing_bogoliubov_transform()
print(f"Shape of matrix W: {transformation_matrix.shape}")
print(f"Orbital energies: {orbital_energies}")
print(f"Transformed constant: {transformed_constant}")
Shape of matrix W: (4, 8)
Orbital energies: [0.29826763 4.38883678 5.5513683 5.64193745]
Transformed constant: -1.9402050758492795
変換行列 \(W\) は、ハミルトニアンの固有ベクトルを作成するための回路を構築するために使用されます。回路は FermionicGaussianState クラスを使用して構築されます。 現在、 Jordan-Wigner 変換 のみがサポートされています。Jordan-Wigner変換の回路は線形の深さを持ち、線形量子ビット接続のみを使用します。 アルゴリズムは Phys. Rev. Applied 9, 044036 からのものです。
[3]:
from qiskit_nature.second_q.circuit.library import FermionicGaussianState
occupied_orbitals = (0, 2)
eig = np.sum(orbital_energies[list(occupied_orbitals)]) + transformed_constant
print(f"Eigenvalue: {eig}")
circuit = FermionicGaussianState(transformation_matrix, occupied_orbitals=occupied_orbitals)
circuit.draw("mpl")
Eigenvalue: 3.909430851761581
[3]:

次のコードセルは回路をシミュレートし、出力状態が実際に予想される固有値を持つハミルトニアンの固有状態であることを検証します。
[4]:
from qiskit.quantum_info import Statevector
from qiskit_nature.second_q.mappers import JordanWignerMapper
# simulate the circuit to get the final state
state = np.array(Statevector(circuit))
# convert the Hamiltonian to a matrix
hamiltonian_jw = JordanWignerMapper().map(hamiltonian_ferm).to_matrix()
# check that the state is an eigenvector with the expected eigenvalue
np.testing.assert_allclose(hamiltonian_jw @ state, eig * state, atol=1e-8)
スレーター行列式#
反対称部分が \(\Delta = 0\) の場合、ハミルトニアンは粒子の数を保存します。この場合、基底変換は消滅演算子ではなく、生成演算子を混合するだけで済みます。
ここで、 \(W\) は \(N \times N\) 行列です。 さらに、軌道エネルギー \(\{\varepsilon_j\}\) は負にすることができます。
[5]:
# create Hamiltonian
hermitian_part = np.array(
[
[1.0, 2.0, 0.0, 0.0],
[2.0, 1.0, 2.0, 0.0],
[0.0, 2.0, 1.0, 2.0],
[0.0, 0.0, 2.0, 1.0],
]
)
constant = 4.0
hamiltonian = QuadraticHamiltonian(
hermitian_part=hermitian_part,
constant=constant,
)
print(f"Hamiltonian conserves particle number: {hamiltonian.conserves_particle_number()}")
Hamiltonian conserves particle number: True
[6]:
# get the transformation matrix W and orbital energies {epsilon_j}
(
transformation_matrix,
orbital_energies,
transformed_constant,
) = hamiltonian.diagonalizing_bogoliubov_transform()
print(f"Shape of matrix W: {transformation_matrix.shape}")
print(f"Orbital energies: {orbital_energies}")
print(f"Transformed constant: {transformed_constant}")
Shape of matrix W: (4, 4)
Orbital energies: [-2.23606798 -0.23606798 2.23606798 4.23606798]
Transformed constant: 4.0
この特殊なケースでは、固有状態はスレイター行列式と呼ばれ、より効率的なアルゴリズムを使用してそれらを準備します。このアルゴリズムには、 FermionicGaussianState の代わりに SlaterDeterminant クラスを使用してアクセスします。 SlaterDeterminant は、占有軌道を入力として受け取りません。代わりに、変換行列の形状を変更できます。 これは \(\eta \times N\) 行列である必要があります。ここで、 \(\eta\) は粒子の数です。
[7]:
from qiskit_nature.second_q.circuit.library import SlaterDeterminant
occupied_orbitals = (0, 2)
eig = np.sum(orbital_energies[list(occupied_orbitals)]) + transformed_constant
print(f"Eigenvalue: {eig}")
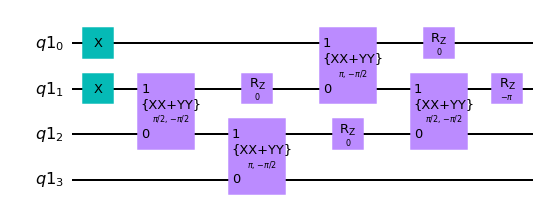
circuit = SlaterDeterminant(transformation_matrix[list(occupied_orbitals)])
circuit.draw("mpl")
Eigenvalue: 4.000000000000001
[7]:
時間発展#
二次ハミルトニアンの下での時間発展は、ハミルトニアンの対角基底に変化することによって容易に実行できます。上記の状態の準備回路は、この基底の変化を反映しますが、計算基底状態 ( すべてゼロの状態と仮定 ) からの状態の準備に最適化され、任意の状態では動作しません。任意の状態で動作する一般ユニタリ基底の変化はBogoliubov変換と呼ばれ、 Qiskit ネイチャーにも実装されています。
以下のコードブロックは、二次ハミルトニアンの時間発展を実装するためのBogoliubov変換の使用法を示しています。
[8]:
from qiskit_nature.second_q.circuit.library import BogoliubovTransform
from qiskit import QuantumCircuit, QuantumRegister
from qiskit.quantum_info import random_hermitian, random_statevector, state_fidelity
from scipy.linalg import expm
# create Hamiltonian
n_modes = 5
hermitian_part = np.array(random_hermitian(n_modes))
hamiltonian = QuadraticHamiltonian(hermitian_part=hermitian_part)
# diagonalize Hamiltonian
(
transformation_matrix,
orbital_energies,
_,
) = hamiltonian.diagonalizing_bogoliubov_transform()
# set simulation time and construct time evolution circuit
time = 1.0
register = QuantumRegister(n_modes)
circuit = QuantumCircuit(register)
bog_circuit = BogoliubovTransform(transformation_matrix)
# change to the diagonal basis of the Hamiltonian
circuit.append(bog_circuit.inverse(), register)
# perform time evolution by applying z rotations
for q, energy in zip(register, orbital_energies):
circuit.rz(-energy * time, q)
# change back to the original basis
circuit.append(bog_circuit, register)
# simulate the circuit
initial_state = random_statevector(2**n_modes)
final_state = initial_state.evolve(circuit)
# compute the correct state by direct exponentiation
hamiltonian_jw = JordanWignerMapper().map(hamiltonian.second_q_op()).to_matrix()
exact_evolution_op = expm(-1j * time * hamiltonian_jw)
expected_state = exact_evolution_op @ np.array(initial_state)
# check that the simulated state is correct
fidelity = state_fidelity(final_state, expected_state)
np.testing.assert_allclose(fidelity, 1.0, atol=1e-8)
[9]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.21.0.dev0+cbc801e |
qiskit-aer | 0.11.0 |
qiskit-nature | 0.4.0 |
| System information | |
| Python version | 3.9.6 |
| Python compiler | GCC 8.5.0 20210514 (Red Hat 8.5.0-3) |
| Python build | default, Aug 11 2021 06:39:25 |
| OS | Linux |
| CPUs | 4 |
| Memory (Gb) | 15.314849853515625 |
| Thu Jun 09 11:38:02 2022 EDT | |
This code is a part of Qiskit
© Copyright IBM 2017, 2022.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.