注釈
このページは docs/tutorials/10_lattice_models.ipynb から生成されました。
格子モデル#
はじめに#
量子物理学(物性物理学や高エネルギー物理学を含む)では、格子上のモデルを研究することがよくあります。たとえば、固体中の電子の振る舞いを考えるとき、原子の位置を格子点として考えることで、格子上に定義されたモデルを研究することができます。このノートブックは、 Lattice クラスを利用して、 LineLattice 、 SquareLattice 、 HyperCubicLattice 、 TriangularLattice 、および一般的な格子などのさまざまな格子システムを生成する方法を示しています。また、格子モデルの例であるフェルミ・ハバードモデルも含まれています。 FermiHubbardModel クラスを使用して、特定の格子の フェルミ・ハバードモデルモデルのハミルトニアンを定義する方法を確認します。
[1]:
from math import pi
import numpy as np
import rustworkx as rx
from qiskit_nature.second_q.hamiltonians.lattices import (
BoundaryCondition,
HyperCubicLattice,
Lattice,
LatticeDrawStyle,
LineLattice,
SquareLattice,
TriangularLattice,
)
from qiskit_nature.second_q.hamiltonians import FermiHubbardModel
LineLattice#
LineLattice は、一次元の格子を提供します。次のように一次元格子を構築することができます。
[2]:
num_nodes = 11
boundary_condition = BoundaryCondition.OPEN
line_lattice = LineLattice(num_nodes=num_nodes, boundary_condition=boundary_condition)
ここでは、それが視覚化されています。
[3]:
line_lattice.draw()

また、 boundary_condition の引数として BoundaryCondition.PERIODIC を指定することにより、周期境界条件を使用して一次元格子を構築することもできます。
[4]:
num_nodes = 11
boundary_condition = BoundaryCondition.PERIODIC
line_lattice = LineLattice(num_nodes=num_nodes, boundary_condition=boundary_condition)
line_lattice.draw()
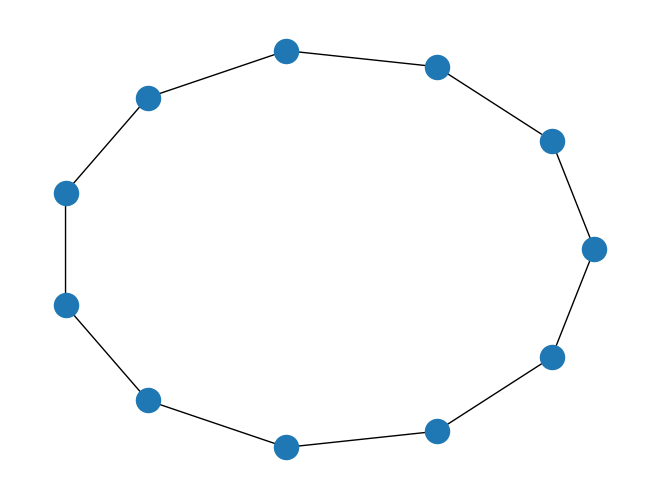
境界条件を無視して格子を描画する場合は、メソッド draw_without_boundary を使用します。
[5]:
line_lattice.draw_without_boundary()

格子のエッジに実数または複素数の重みを定義できます。これは、引数 edge_parameter に値を与えることによって行われます。 onsite_parameter の値を渡すことにより、格子の自己ループの値を指定することもできます。
[6]:
num_nodes = 11
boundary_condition = BoundaryCondition.PERIODIC
edge_parameter = 1.0 + 1.0j
onsite_parameter = 1.0
line_lattice = LineLattice(
num_nodes=num_nodes,
edge_parameter=edge_parameter,
onsite_parameter=onsite_parameter,
boundary_condition=boundary_condition,
)
set(line_lattice.graph.weighted_edge_list())
[6]:
{(0, 0, 1.0),
(0, 1, (1+1j)),
(0, 10, (1-1j)),
(1, 1, 1.0),
(1, 2, (1+1j)),
(2, 2, 1.0),
(2, 3, (1+1j)),
(3, 3, 1.0),
(3, 4, (1+1j)),
(4, 4, 1.0),
(4, 5, (1+1j)),
(5, 5, 1.0),
(5, 6, (1+1j)),
(6, 6, 1.0),
(6, 7, (1+1j)),
(7, 7, 1.0),
(7, 8, (1+1j)),
(8, 8, 1.0),
(8, 9, (1+1j)),
(9, 9, 1.0),
(9, 10, (1+1j)),
(10, 10, 1.0)}
格子の接続性は、 to_adjacency_matrix によって実行される隣接行列と見なすことができます。
[7]:
line_lattice.to_adjacency_matrix()
[7]:
array([[1., 1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
[1., 1., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 1., 1., 1., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 1., 1., 1., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 1., 1., 1., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 1., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 1., 1., 1., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1.]])
weighted=True を設定することにより、行列要素が重みとなっているエルミート行列を取得します。
[8]:
line_lattice.to_adjacency_matrix(weighted=True)
[8]:
array([[1.+0.j, 1.+1.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j,
0.+0.j, 0.+0.j, 1.-1.j],
[1.-1.j, 1.+0.j, 1.+1.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j,
0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 1.-1.j, 1.+0.j, 1.+1.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j,
0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 1.-1.j, 1.+0.j, 1.+1.j, 0.+0.j, 0.+0.j, 0.+0.j,
0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 1.-1.j, 1.+0.j, 1.+1.j, 0.+0.j, 0.+0.j,
0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 1.-1.j, 1.+0.j, 1.+1.j, 0.+0.j,
0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 1.-1.j, 1.+0.j, 1.+1.j,
0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 1.-1.j, 1.+0.j,
1.+1.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 1.-1.j,
1.+0.j, 1.+1.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j,
1.-1.j, 1.+0.j, 1.+1.j],
[1.+1.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j,
0.+0.j, 1.-1.j, 1.+0.j]])
SquareLattice#
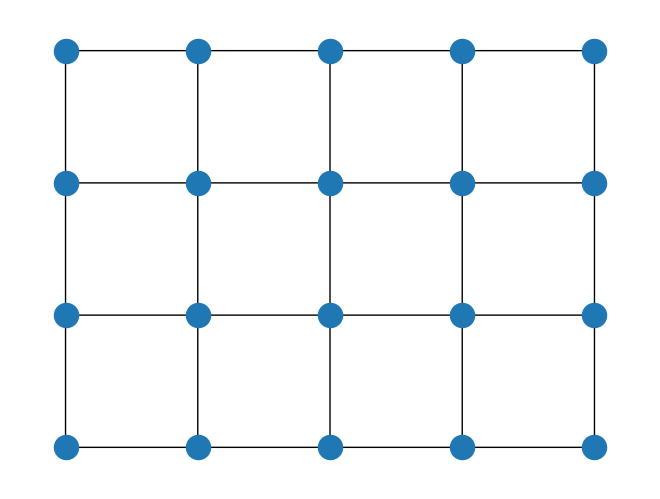
SquareLattice は二次元の格子を提供します。ここでは、開いた境界条件で二次元格子を作成します。
[9]:
rows = 5
cols = 4
boundary_condition = BoundaryCondition.OPEN
square_lattice = SquareLattice(rows=rows, cols=cols, boundary_condition=boundary_condition)
square_lattice.draw()
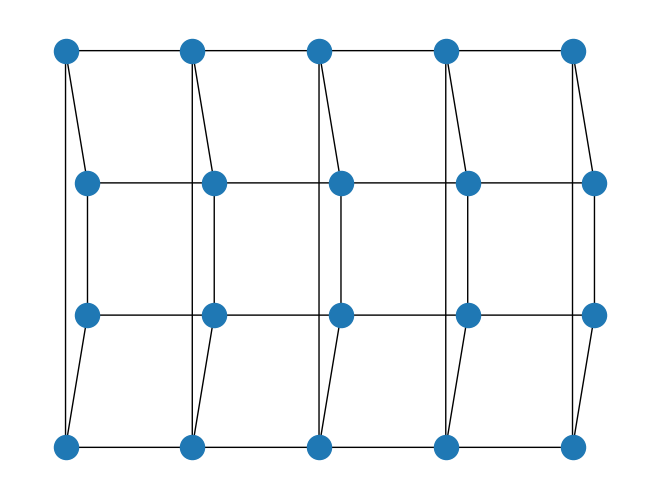
border_condition をタプルとして設定することにより、各方向の境界条件を指定できます。
[10]:
rows = 5
cols = 4
boundary_condition = (
BoundaryCondition.OPEN,
BoundaryCondition.PERIODIC,
) # open in the x-direction, periodic in the y-direction
square_lattice = SquareLattice(rows=rows, cols=cols, boundary_condition=boundary_condition)
square_lattice.draw()
ここでも、格子のエッジと自己ループに重みを付けることができます。ここでは、各方向にタプルとして重みを付けることができます。
[11]:
rows = 5
cols = 4
edge_parameter = (1.0, 1.0 + 1.0j)
boundary_condition = (
BoundaryCondition.OPEN,
BoundaryCondition.PERIODIC,
) # open in the x-direction, periodic in the y-direction
onsite_parameter = 1.0
square_lattice = SquareLattice(
rows=rows,
cols=cols,
edge_parameter=edge_parameter,
onsite_parameter=onsite_parameter,
boundary_condition=boundary_condition,
)
set(square_lattice.graph.weighted_edge_list())
[11]:
{(0, 0, 1.0),
(0, 1, 1.0),
(0, 5, (1+1j)),
(0, 15, (1-1j)),
(1, 1, 1.0),
(1, 2, 1.0),
(1, 6, (1+1j)),
(1, 16, (1-1j)),
(2, 2, 1.0),
(2, 3, 1.0),
(2, 7, (1+1j)),
(2, 17, (1-1j)),
(3, 3, 1.0),
(3, 4, 1.0),
(3, 8, (1+1j)),
(3, 18, (1-1j)),
(4, 4, 1.0),
(4, 9, (1+1j)),
(4, 19, (1-1j)),
(5, 5, 1.0),
(5, 6, 1.0),
(5, 10, (1+1j)),
(6, 6, 1.0),
(6, 7, 1.0),
(6, 11, (1+1j)),
(7, 7, 1.0),
(7, 8, 1.0),
(7, 12, (1+1j)),
(8, 8, 1.0),
(8, 9, 1.0),
(8, 13, (1+1j)),
(9, 9, 1.0),
(9, 14, (1+1j)),
(10, 10, 1.0),
(10, 11, 1.0),
(10, 15, (1+1j)),
(11, 11, 1.0),
(11, 12, 1.0),
(11, 16, (1+1j)),
(12, 12, 1.0),
(12, 13, 1.0),
(12, 17, (1+1j)),
(13, 13, 1.0),
(13, 14, 1.0),
(13, 18, (1+1j)),
(14, 14, 1.0),
(14, 19, (1+1j)),
(15, 15, 1.0),
(15, 16, 1.0),
(16, 16, 1.0),
(16, 17, 1.0),
(17, 17, 1.0),
(17, 18, 1.0),
(18, 18, 1.0),
(18, 19, 1.0),
(19, 19, 1.0)}
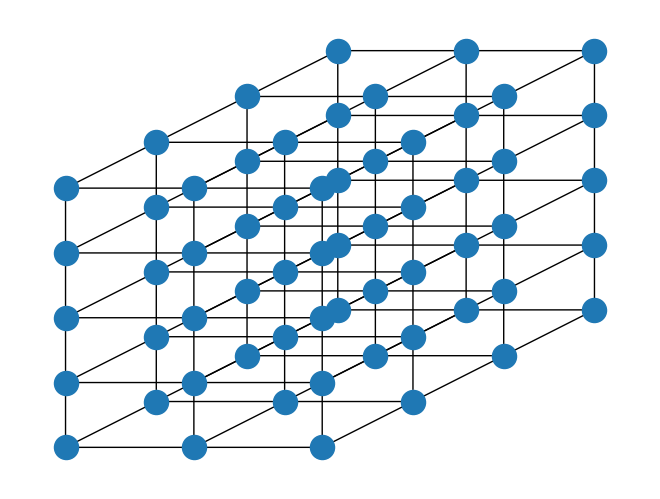
HyperCubicLattice#
HyperCubicLattice は、 LineLattice と SquareLattice を一般化したものです。任意のd次元格子を提供します。ここでは、例としてサイズ 3 x 4 x5 の三次元格子を作成します。サイズはタプルとして指定され、境界条件は方向ごとに指定することもできます。この例では、境界条件は開いています。
[12]:
size = (3, 4, 5)
boundary_condition = (
BoundaryCondition.OPEN,
BoundaryCondition.OPEN,
BoundaryCondition.OPEN,
)
cubic_lattice = HyperCubicLattice(size=size, boundary_condition=boundary_condition)
格子点の位置を指定して立方格子を描画します。
[13]:
# function for setting the positions
def indextocoord_3d(index: int, size: tuple, angle) -> list:
z = index // (size[0] * size[1])
a = index % (size[0] * size[1])
y = a // size[0]
x = a % size[0]
vec_x = np.array([1, 0])
vec_y = np.array([np.cos(angle), np.sin(angle)])
vec_z = np.array([0, 1])
return_coord = x * vec_x + y * vec_y + z * vec_z
return return_coord.tolist()
pos = dict([(index, indextocoord_3d(index, size, angle=pi / 4)) for index in range(np.prod(size))])
cubic_lattice.draw(style=LatticeDrawStyle(pos=pos))
TriangularLattice#
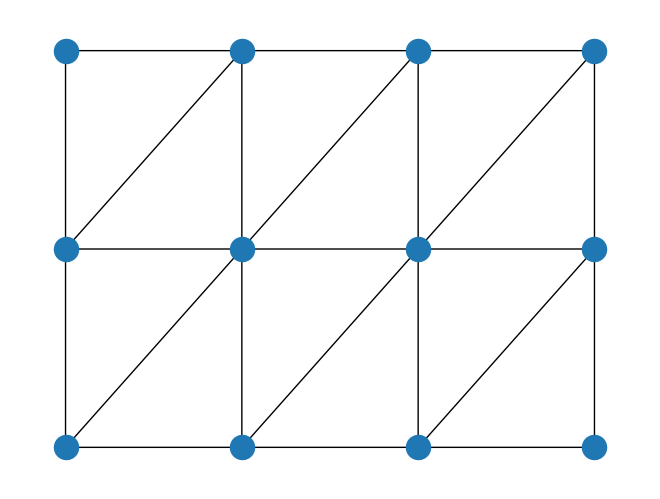
TriangularLattice は三角形の格子を提供します。これは、対角線のエッジを持つ二次元の格子と見なすことができます。引数 boundary_condition は、 「open」 または 「periodic」 のいずれかを取ることができます。
[14]:
rows = 4
cols = 3
boundary_condition = BoundaryCondition.OPEN
triangular_lattice = TriangularLattice(rows=rows, cols=cols, boundary_condition=boundary_condition)
triangular_lattice.draw()
[15]:
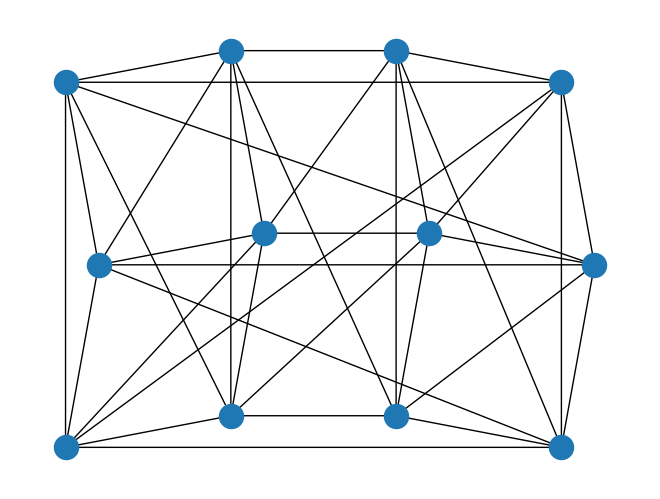
rows = 4
cols = 3
boundary_condition = BoundaryCondition.PERIODIC
triangular_lattice = TriangularLattice(rows=rows, cols=cols, boundary_condition=boundary_condition)
triangular_lattice.draw()
一般的な格子#
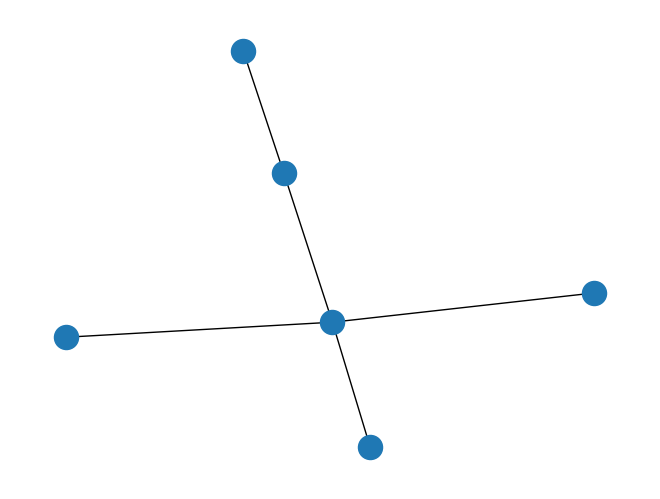
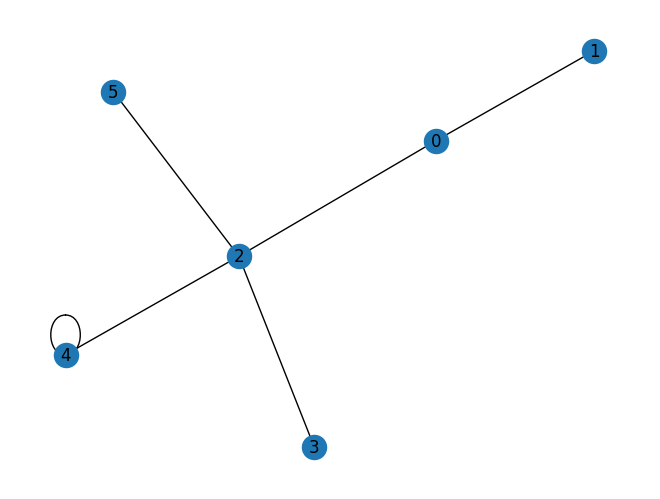
上記では、並進不変格子を見てきました。ここでは、一般的な格子について考えます。PyGraph のインスタンスを使用して、ノードとエッジで構成される一般的な格子を構築できます。
[16]:
graph = rx.PyGraph(multigraph=False) # multigraph shoud be False
graph.add_nodes_from(range(6))
weighted_edge_list = [
(0, 1, 1.0 + 1.0j),
(0, 2, -1.0),
(2, 3, 2.0),
(4, 2, -1.0 + 2.0j),
(4, 4, 3.0),
(2, 5, -1.0),
]
graph.add_edges_from(weighted_edge_list)
# make a lattice
general_lattice = Lattice(graph)
set(general_lattice.graph.weighted_edge_list())
[16]:
{(0, 1, (1+1j)),
(0, 2, -1.0),
(2, 3, 2.0),
(2, 5, -1.0),
(4, 2, (-1+2j)),
(4, 4, 3.0)}
これがその可視化です。
[17]:
general_lattice.draw()
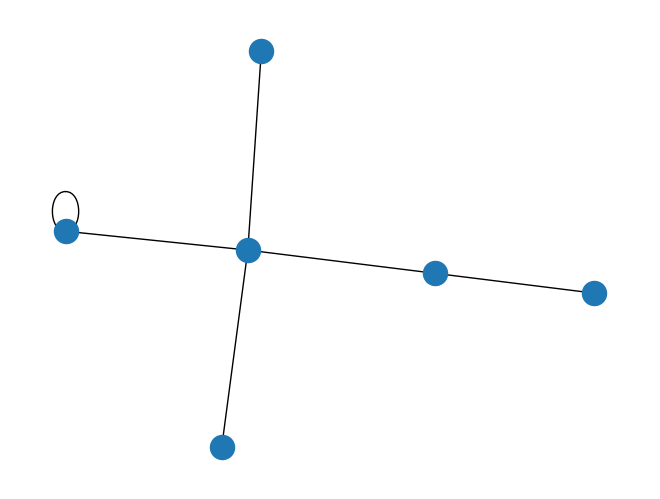
格子内の自己ループを視覚化する場合は、 self_loop を True に設定します。
[18]:
general_lattice.draw(self_loop=True)
with_labels が True の場合、格子サイトのラベルが描画されます。
[19]:
general_lattice.draw(self_loop=True, style=LatticeDrawStyle(with_labels=True))
フェルミ・ハバードモデル#
フェルミ・ハバードモデルは、格子上を移動する電子と同じサイトでの相互作用を表す最も単純なモデルです。ハミルトニアンは次のように与えられます。
ここで、 \(c_{i, \sigma}^\dagger\) と \(c_{i, \sigma}\) は、スピン \(\sigma\) を伴うサイト \(i\) でのフェルミ粒子の生成および消滅演算子です。演算子 \(n_{i, \sigma}\) は、 \(n_{i, \sigma} = c_{i, \sigma}^\dagger c_{i, \sigma}\) で定義される個数演算子です。 行列 \(t_{i, j}\) は、相互作用行列と呼ばれるエルミート行列です。 パラメータ \(U\) は、相互作用の強さを表します。
FermiHubbardModel クラスを使用して、特定の格子の対応するハミルトニアンを生成できます。ここでは、二次元格子上に均一な相互作用と相互作用パラメーターを持つハミルトニアンを構築します。
[20]:
square_lattice = SquareLattice(rows=5, cols=4, boundary_condition=BoundaryCondition.PERIODIC)
t = -1.0 # the interaction parameter
v = 0.0 # the onsite potential
u = 5.0 # the interaction parameter U
fhm = FermiHubbardModel(
square_lattice.uniform_parameters(
uniform_interaction=t,
uniform_onsite_potential=v,
),
onsite_interaction=u,
)
フェルミ粒子演算子の観点からハミルトニアンを取得するには、 second_q_ops メソッドを使用します。ハミルトニアンは FermionicOp のインスタンスとして返されます。
注記
スピンの自由度のため、必要なフェルミ粒子演算子の数は格子サイトの数の2倍です。
実装では、偶数インデックスはアップスピンに対応し、奇数インデックスはダウンスピンに対応します。
[21]:
ham = fhm.second_q_op().simplify()
print(ham)
Fermionic Operator
number spin orbitals=40, number terms=180
(-1+0j) * ( +_0 -_2 )
+ (1+0j) * ( -_0 +_2 )
+ (-1+0j) * ( +_0 -_10 )
+ (1+0j) * ( -_0 +_10 )
+ (-1+0j) * ( +_10 -_12 )
+ (1+0j) * ( -_10 +_12 )
+ (-1+0j) * ( +_10 -_20 )
+ (1+0j) * ( -_10 +_20 )
+ (-1+0j) * ( +_20 -_22 )
+ (1+0j) * ( -_20 +_22 )
+ (-1+0j) * ( +_20 -_30 )
+ (1+0j) * ( -_20 +_30 )
+ (-1+0j) * ( +_30 -_32 )
+ (1+0j) * ( -_30 +_32 )
+ (-1+0j) * ( +_2 -_4 )
+ (1+0j) * ( -_2 +_4 )
+ (-1+0j) * ( +_2 -_12 )
+ (1+0j) * ( -_2 +_12 )
+ (-1+0j) * ( +_12 -_14 )
+ (1+0j) * ( -_12 +_14 )
+ (-1+0j) * ( +_12 -_22 )
+ (1+0j) * ( -_12 +_22 )
+ (-1+0j) * ( +_22 -_24 )
+ (1+0j) * ( -_22 +_24 )
+ (-1+0j) * ( +_22 -_32 )
+ (1+0j) * ( -_22 +_32 )
+ (-1+0j) * ( +_32 -_34 )
+ (1+0j) * ( -_32 +_34 )
+ (-1+0j) * ( +_4 -_6 )
+ (1+0j) * ( -_4 +_6 )
+ (-1+0j) * ( +_4 -_14 )
+ (1+0j) * ( -_4 +_14 )
+ (-1+0j) * ( +_14 -_16 )
+ (1+0j) * ( -_14 +_16 )
+ (-1+0j) * ( +_14 -_24 )
+ (1+0j) * ( -_14 +_24 )
+ (-1+0j) * ( +_24 -_26 )
+ (1+0j) * ( -_24 +_26 )
+ (-1+0j) * ( +_24 -_34 )
+ (1+0j) * ( -_24 +_34 )
+ (-1+0j) * ( +_34 -_36 )
+ (1+0j) * ( -_34 +_36 )
+ (-1+0j) * ( +_6 -_8 )
+ (1+0j) * ( -_6 +_8 )
+ (-1+0j) * ( +_6 -_16 )
+ (1+0j) * ( -_6 +_16 )
+ (-1+0j) * ( +_16 -_18 )
+ (1+0j) * ( -_16 +_18 )
+ (-1+0j) * ( +_16 -_26 )
+ (1+0j) * ( -_16 +_26 )
+ (-1+0j) * ( +_26 -_28 )
+ (1+0j) * ( -_26 +_28 )
+ (-1+0j) * ( +_26 -_36 )
+ (1+0j) * ( -_26 +_36 )
+ (-1+0j) * ( +_36 -_38 )
+ (1+0j) * ( -_36 +_38 )
+ (-1+0j) * ( +_8 -_18 )
+ (1+0j) * ( -_8 +_18 )
+ (-1+0j) * ( +_18 -_28 )
+ (1+0j) * ( -_18 +_28 )
+ (-1+0j) * ( +_28 -_38 )
+ (1+0j) * ( -_28 +_38 )
+ (-1+0j) * ( +_0 -_8 )
+ (1+0j) * ( -_0 +_8 )
+ (-1+0j) * ( +_10 -_18 )
+ (1+0j) * ( -_10 +_18 )
+ (-1+0j) * ( +_20 -_28 )
+ (1+0j) * ( -_20 +_28 )
+ (-1+0j) * ( +_30 -_38 )
+ (1+0j) * ( -_30 +_38 )
+ (-1+0j) * ( +_0 -_30 )
+ (1+0j) * ( -_0 +_30 )
+ (-1+0j) * ( +_2 -_32 )
+ (1+0j) * ( -_2 +_32 )
+ (-1+0j) * ( +_4 -_34 )
+ (1+0j) * ( -_4 +_34 )
+ (-1+0j) * ( +_6 -_36 )
+ (1+0j) * ( -_6 +_36 )
+ (-1+0j) * ( +_8 -_38 )
+ (1+0j) * ( -_8 +_38 )
+ (-1+0j) * ( +_1 -_3 )
+ (1+0j) * ( -_1 +_3 )
+ (-1+0j) * ( +_1 -_11 )
+ (1+0j) * ( -_1 +_11 )
+ (-1+0j) * ( +_11 -_13 )
+ (1+0j) * ( -_11 +_13 )
+ (-1+0j) * ( +_11 -_21 )
+ (1+0j) * ( -_11 +_21 )
+ (-1+0j) * ( +_21 -_23 )
+ (1+0j) * ( -_21 +_23 )
+ (-1+0j) * ( +_21 -_31 )
+ (1+0j) * ( -_21 +_31 )
+ (-1+0j) * ( +_31 -_33 )
+ (1+0j) * ( -_31 +_33 )
+ (-1+0j) * ( +_3 -_5 )
+ (1+0j) * ( -_3 +_5 )
+ (-1+0j) * ( +_3 -_13 )
+ (1+0j) * ( -_3 +_13 )
+ (-1+0j) * ( +_13 -_15 )
+ (1+0j) * ( -_13 +_15 )
+ (-1+0j) * ( +_13 -_23 )
+ (1+0j) * ( -_13 +_23 )
+ (-1+0j) * ( +_23 -_25 )
+ (1+0j) * ( -_23 +_25 )
+ (-1+0j) * ( +_23 -_33 )
+ (1+0j) * ( -_23 +_33 )
+ (-1+0j) * ( +_33 -_35 )
+ (1+0j) * ( -_33 +_35 )
+ (-1+0j) * ( +_5 -_7 )
+ (1+0j) * ( -_5 +_7 )
+ (-1+0j) * ( +_5 -_15 )
+ (1+0j) * ( -_5 +_15 )
+ (-1+0j) * ( +_15 -_17 )
+ (1+0j) * ( -_15 +_17 )
+ (-1+0j) * ( +_15 -_25 )
+ (1+0j) * ( -_15 +_25 )
+ (-1+0j) * ( +_25 -_27 )
+ (1+0j) * ( -_25 +_27 )
+ (-1+0j) * ( +_25 -_35 )
+ (1+0j) * ( -_25 +_35 )
+ (-1+0j) * ( +_35 -_37 )
+ (1+0j) * ( -_35 +_37 )
+ (-1+0j) * ( +_7 -_9 )
+ (1+0j) * ( -_7 +_9 )
+ (-1+0j) * ( +_7 -_17 )
+ (1+0j) * ( -_7 +_17 )
+ (-1+0j) * ( +_17 -_19 )
+ (1+0j) * ( -_17 +_19 )
+ (-1+0j) * ( +_17 -_27 )
+ (1+0j) * ( -_17 +_27 )
+ (-1+0j) * ( +_27 -_29 )
+ (1+0j) * ( -_27 +_29 )
+ (-1+0j) * ( +_27 -_37 )
+ (1+0j) * ( -_27 +_37 )
+ (-1+0j) * ( +_37 -_39 )
+ (1+0j) * ( -_37 +_39 )
+ (-1+0j) * ( +_9 -_19 )
+ (1+0j) * ( -_9 +_19 )
+ (-1+0j) * ( +_19 -_29 )
+ (1+0j) * ( -_19 +_29 )
+ (-1+0j) * ( +_29 -_39 )
+ (1+0j) * ( -_29 +_39 )
+ (-1+0j) * ( +_1 -_9 )
+ (1+0j) * ( -_1 +_9 )
+ (-1+0j) * ( +_11 -_19 )
+ (1+0j) * ( -_11 +_19 )
+ (-1+0j) * ( +_21 -_29 )
+ (1+0j) * ( -_21 +_29 )
+ (-1+0j) * ( +_31 -_39 )
+ (1+0j) * ( -_31 +_39 )
+ (-1+0j) * ( +_1 -_31 )
+ (1+0j) * ( -_1 +_31 )
+ (-1+0j) * ( +_3 -_33 )
+ (1+0j) * ( -_3 +_33 )
+ (-1+0j) * ( +_5 -_35 )
+ (1+0j) * ( -_5 +_35 )
+ (-1+0j) * ( +_7 -_37 )
+ (1+0j) * ( -_7 +_37 )
+ (-1+0j) * ( +_9 -_39 )
+ (1+0j) * ( -_9 +_39 )
+ (5+0j) * ( +_0 -_0 +_1 -_1 )
+ (5+0j) * ( +_2 -_2 +_3 -_3 )
+ (5+0j) * ( +_4 -_4 +_5 -_5 )
+ (5+0j) * ( +_6 -_6 +_7 -_7 )
+ (5+0j) * ( +_8 -_8 +_9 -_9 )
+ (5+0j) * ( +_10 -_10 +_11 -_11 )
+ (5+0j) * ( +_12 -_12 +_13 -_13 )
+ (5+0j) * ( +_14 -_14 +_15 -_15 )
+ (5+0j) * ( +_16 -_16 +_17 -_17 )
+ (5+0j) * ( +_18 -_18 +_19 -_19 )
+ (5+0j) * ( +_20 -_20 +_21 -_21 )
+ (5+0j) * ( +_22 -_22 +_23 -_23 )
+ (5+0j) * ( +_24 -_24 +_25 -_25 )
+ (5+0j) * ( +_26 -_26 +_27 -_27 )
+ (5+0j) * ( +_28 -_28 +_29 -_29 )
+ (5+0j) * ( +_30 -_30 +_31 -_31 )
+ (5+0j) * ( +_32 -_32 +_33 -_33 )
+ (5+0j) * ( +_34 -_34 +_35 -_35 )
+ (5+0j) * ( +_36 -_36 +_37 -_37 )
+ (5+0j) * ( +_38 -_38 +_39 -_39 )
Lattice のエッジには重みがあるため、格子インスタンスを使用して一般的な相互作用行列を定義できます。ここでは、不均一な相互作用パラメータが与えられている一般的な格子上のフェルミ・ハバードモデルを検討します。この場合、格子の重みは相互作用行列と見なされます。ハミルトニアン( second_q_ops )を生成した後、量子ビットマッパーを使用して量子ビット演算子を生成したり、使用可能なアルゴリズムのいずれかを使用して対応する格子問題を解決したりできます。
[22]:
graph = rx.PyGraph(multigraph=False) # multiigraph shoud be False
graph.add_nodes_from(range(6))
weighted_edge_list = [
(0, 1, 1.0 + 1.0j),
(0, 2, -1.0),
(2, 3, 2.0),
(4, 2, -1.0 + 2.0j),
(4, 4, 3.0),
(2, 5, -1.0),
]
graph.add_edges_from(weighted_edge_list)
general_lattice = Lattice(graph) # the lattice whose weights are seen as the interaction matrix.
u = 5.0 # the interaction parameter U
fhm = FermiHubbardModel(lattice=general_lattice, onsite_interaction=u)
ham = fhm.second_q_op().simplify()
print(ham)
Fermionic Operator
number spin orbitals=12, number terms=28
(1+1j) * ( +_0 -_2 )
+ (-1+1j) * ( -_0 +_2 )
+ (-1+0j) * ( +_0 -_4 )
+ (1+0j) * ( -_0 +_4 )
+ (2+0j) * ( +_4 -_6 )
+ (-2+0j) * ( -_4 +_6 )
+ (-1-2j) * ( +_4 -_8 )
+ (1-2j) * ( -_4 +_8 )
+ (3+0j) * ( +_8 -_8 )
+ (-1+0j) * ( +_4 -_10 )
+ (1+0j) * ( -_4 +_10 )
+ (1+1j) * ( +_1 -_3 )
+ (-1+1j) * ( -_1 +_3 )
+ (-1+0j) * ( +_1 -_5 )
+ (1+0j) * ( -_1 +_5 )
+ (2+0j) * ( +_5 -_7 )
+ (-2+0j) * ( -_5 +_7 )
+ (-1-2j) * ( +_5 -_9 )
+ (1-2j) * ( -_5 +_9 )
+ (3+0j) * ( +_9 -_9 )
+ (-1+0j) * ( +_5 -_11 )
+ (1+0j) * ( -_5 +_11 )
+ (5+0j) * ( +_0 -_0 +_1 -_1 )
+ (5+0j) * ( +_2 -_2 +_3 -_3 )
+ (5+0j) * ( +_4 -_4 +_5 -_5 )
+ (5+0j) * ( +_6 -_6 +_7 -_7 )
+ (5+0j) * ( +_8 -_8 +_9 -_9 )
+ (5+0j) * ( +_10 -_10 +_11 -_11 )
格子モデル問題#
Qiskit Natureには、 LatticeModelProblem クラスもあります。これにより、 GroundStateEigensolver を使用して、特定の格子の基底状態エネルギーを計算できます。このクラスは次のように使用できます。
[23]:
from qiskit_nature.second_q.problems import LatticeModelProblem
num_nodes = 4
boundary_condition = BoundaryCondition.OPEN
line_lattice = LineLattice(num_nodes=num_nodes, boundary_condition=boundary_condition)
fhm = FermiHubbardModel(
line_lattice.uniform_parameters(
uniform_interaction=t,
uniform_onsite_potential=v,
),
onsite_interaction=u,
)
lmp = LatticeModelProblem(fhm)
[24]:
from qiskit_algorithms import NumPyMinimumEigensolver
from qiskit_nature.second_q.algorithms import GroundStateEigensolver
from qiskit_nature.second_q.mappers import JordanWignerMapper
numpy_solver = NumPyMinimumEigensolver()
qubit_mapper = JordanWignerMapper()
calc = GroundStateEigensolver(qubit_mapper, numpy_solver)
res = calc.solve(lmp)
print(res)
=== GROUND STATE ===
* Lattice ground state energy : -2.566350190841
[25]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.24.0.dev0+2b3686f |
qiskit-aer | 0.11.2 |
qiskit-ibmq-provider | 0.19.2 |
qiskit-nature | 0.6.0 |
| System information | |
| Python version | 3.9.16 |
| Python compiler | GCC 12.2.1 20221121 (Red Hat 12.2.1-4) |
| Python build | main, Dec 7 2022 00:00:00 |
| OS | Linux |
| CPUs | 8 |
| Memory (Gb) | 62.50002670288086 |
| Thu Apr 06 09:13:58 2023 CEST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.