নোট
This page was generated from docs/tutorials/10_lattice_models.ipynb.
Lattice models#
Introduction#
In quantum physics (including condensed matter physics and high energy physics) we often study models on lattices. For example, when we think about behavior of electrons in a solid, we can study a model defined on a lattice by considering the positions of atoms as lattice points. This notebook demonstrates how we can utilize Lattice classes to generate various lattice systems such as LineLattice, SquareLattice, HyperCubicLattice, TriangularLattice, and a general lattice. It
also includes an example of a lattice model, the Fermi-Hubbard model. We see how we can define the Hamiltonian of the Fermi-Hubbard model for a given lattice using FermiHubbardModel class.
[1]:
from math import pi
import numpy as np
import rustworkx as rx
from qiskit_nature.second_q.hamiltonians.lattices import (
BoundaryCondition,
HyperCubicLattice,
Lattice,
LatticeDrawStyle,
LineLattice,
SquareLattice,
TriangularLattice,
)
from qiskit_nature.second_q.hamiltonians import FermiHubbardModel
LineLattice#
LineLattice provides a one-dimensional lattice. We can construct a one-dimensional lattice as follows.
[2]:
num_nodes = 11
boundary_condition = BoundaryCondition.OPEN
line_lattice = LineLattice(num_nodes=num_nodes, boundary_condition=boundary_condition)
Here, it is visualized.
[3]:
line_lattice.draw()

We can also construct a one-dimensional lattice with the periodic boundary conditions by specifying BoundaryCondition.PERIODIC as the argument of boundary_condition.
[4]:
num_nodes = 11
boundary_condition = BoundaryCondition.PERIODIC
line_lattice = LineLattice(num_nodes=num_nodes, boundary_condition=boundary_condition)
line_lattice.draw()
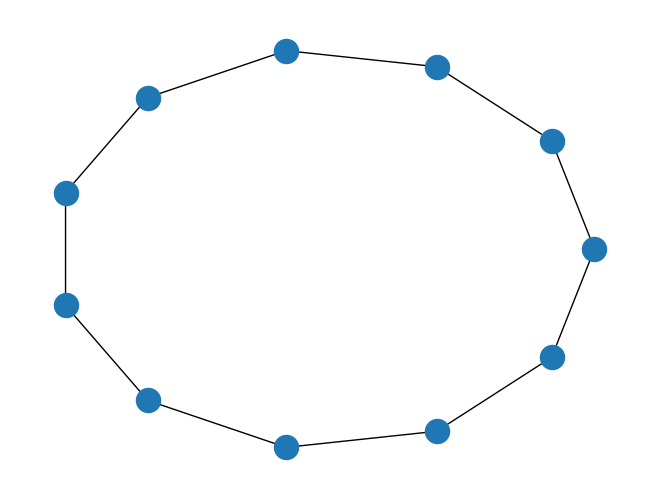
When we want to draw the lattice ignoring the boundary conditions, we use the method draw_without_boundary.
[5]:
line_lattice.draw_without_boundary()

We can define real or complex weights for the edges of the lattice. This is done by giving a value to the argument edge_parameter. We can also give a value for the self-loops of the lattice by passing the value for onsite_parameter.
[6]:
num_nodes = 11
boundary_condition = BoundaryCondition.PERIODIC
edge_parameter = 1.0 + 1.0j
onsite_parameter = 1.0
line_lattice = LineLattice(
num_nodes=num_nodes,
edge_parameter=edge_parameter,
onsite_parameter=onsite_parameter,
boundary_condition=boundary_condition,
)
set(line_lattice.graph.weighted_edge_list())
[6]:
{(0, 0, 1.0),
(0, 1, (1+1j)),
(0, 10, (1-1j)),
(1, 1, 1.0),
(1, 2, (1+1j)),
(2, 2, 1.0),
(2, 3, (1+1j)),
(3, 3, 1.0),
(3, 4, (1+1j)),
(4, 4, 1.0),
(4, 5, (1+1j)),
(5, 5, 1.0),
(5, 6, (1+1j)),
(6, 6, 1.0),
(6, 7, (1+1j)),
(7, 7, 1.0),
(7, 8, (1+1j)),
(8, 8, 1.0),
(8, 9, (1+1j)),
(9, 9, 1.0),
(9, 10, (1+1j)),
(10, 10, 1.0)}
The connectivity of the lattice can be seen as the adjacency matrix, which is done by to_adjacency_matrix.
[7]:
line_lattice.to_adjacency_matrix()
[7]:
array([[1., 1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
[1., 1., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 1., 1., 1., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 1., 1., 1., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 1., 1., 1., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 1., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 1., 1., 1., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1.]])
By setting weighted=True, we obtain a Hermitian matrix whose matrix elements are the weights.
[8]:
line_lattice.to_adjacency_matrix(weighted=True)
[8]:
array([[1.+0.j, 1.+1.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j,
0.+0.j, 0.+0.j, 1.-1.j],
[1.-1.j, 1.+0.j, 1.+1.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j,
0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 1.-1.j, 1.+0.j, 1.+1.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j,
0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 1.-1.j, 1.+0.j, 1.+1.j, 0.+0.j, 0.+0.j, 0.+0.j,
0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 1.-1.j, 1.+0.j, 1.+1.j, 0.+0.j, 0.+0.j,
0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 1.-1.j, 1.+0.j, 1.+1.j, 0.+0.j,
0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 1.-1.j, 1.+0.j, 1.+1.j,
0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 1.-1.j, 1.+0.j,
1.+1.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 1.-1.j,
1.+0.j, 1.+1.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j,
1.-1.j, 1.+0.j, 1.+1.j],
[1.+1.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j,
0.+0.j, 1.-1.j, 1.+0.j]])
SquareLattice#
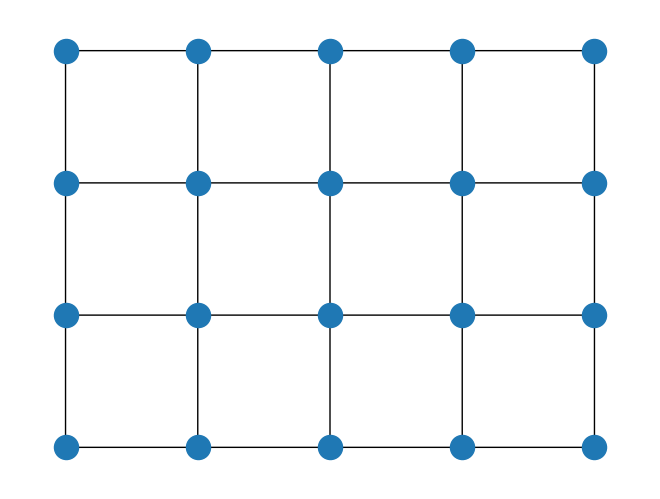
SquareLattice provides a two-dimensional lattice. Here, we make a two-dimensional lattice with the open boundary conditions.
[9]:
rows = 5
cols = 4
boundary_condition = BoundaryCondition.OPEN
square_lattice = SquareLattice(rows=rows, cols=cols, boundary_condition=boundary_condition)
square_lattice.draw()
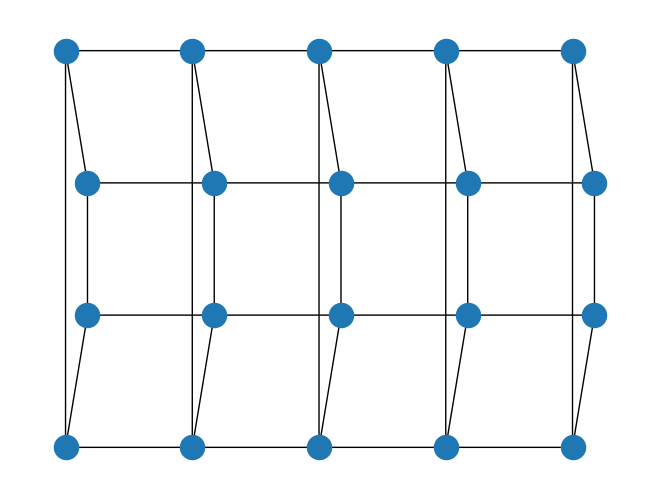
We can specify the boundary conditions for each direction by setting boundary_condition as a tuple.
[10]:
rows = 5
cols = 4
boundary_condition = (
BoundaryCondition.OPEN,
BoundaryCondition.PERIODIC,
) # open in the x-direction, periodic in the y-direction
square_lattice = SquareLattice(rows=rows, cols=cols, boundary_condition=boundary_condition)
square_lattice.draw()
Again, we can give weights on the edges and the self-loops of the lattice. Here, it is possible to give weights for each direction as a tuple.
[11]:
rows = 5
cols = 4
edge_parameter = (1.0, 1.0 + 1.0j)
boundary_condition = (
BoundaryCondition.OPEN,
BoundaryCondition.PERIODIC,
) # open in the x-direction, periodic in the y-direction
onsite_parameter = 1.0
square_lattice = SquareLattice(
rows=rows,
cols=cols,
edge_parameter=edge_parameter,
onsite_parameter=onsite_parameter,
boundary_condition=boundary_condition,
)
set(square_lattice.graph.weighted_edge_list())
[11]:
{(0, 0, 1.0),
(0, 1, 1.0),
(0, 5, (1+1j)),
(0, 15, (1-1j)),
(1, 1, 1.0),
(1, 2, 1.0),
(1, 6, (1+1j)),
(1, 16, (1-1j)),
(2, 2, 1.0),
(2, 3, 1.0),
(2, 7, (1+1j)),
(2, 17, (1-1j)),
(3, 3, 1.0),
(3, 4, 1.0),
(3, 8, (1+1j)),
(3, 18, (1-1j)),
(4, 4, 1.0),
(4, 9, (1+1j)),
(4, 19, (1-1j)),
(5, 5, 1.0),
(5, 6, 1.0),
(5, 10, (1+1j)),
(6, 6, 1.0),
(6, 7, 1.0),
(6, 11, (1+1j)),
(7, 7, 1.0),
(7, 8, 1.0),
(7, 12, (1+1j)),
(8, 8, 1.0),
(8, 9, 1.0),
(8, 13, (1+1j)),
(9, 9, 1.0),
(9, 14, (1+1j)),
(10, 10, 1.0),
(10, 11, 1.0),
(10, 15, (1+1j)),
(11, 11, 1.0),
(11, 12, 1.0),
(11, 16, (1+1j)),
(12, 12, 1.0),
(12, 13, 1.0),
(12, 17, (1+1j)),
(13, 13, 1.0),
(13, 14, 1.0),
(13, 18, (1+1j)),
(14, 14, 1.0),
(14, 19, (1+1j)),
(15, 15, 1.0),
(15, 16, 1.0),
(16, 16, 1.0),
(16, 17, 1.0),
(17, 17, 1.0),
(17, 18, 1.0),
(18, 18, 1.0),
(18, 19, 1.0),
(19, 19, 1.0)}
HyperCubicLattice#
HyperCubicLattice is a generalization of LineLattice and SquareLattice. It provides an arbitrary d-dimensional lattice. Here, we make a three-dimensional lattice of size 3 by 4 by 5 as an example. The size is given as a tuple, and the boundary conditions can be specified for each direction too. In the example, the boundary conditions are open.
[12]:
size = (3, 4, 5)
boundary_condition = (
BoundaryCondition.OPEN,
BoundaryCondition.OPEN,
BoundaryCondition.OPEN,
)
cubic_lattice = HyperCubicLattice(size=size, boundary_condition=boundary_condition)
We draw the cubic lattice specifying the positions of the lattice points.
[13]:
# function for setting the positions
def indextocoord_3d(index: int, size: tuple, angle) -> list:
z = index // (size[0] * size[1])
a = index % (size[0] * size[1])
y = a // size[0]
x = a % size[0]
vec_x = np.array([1, 0])
vec_y = np.array([np.cos(angle), np.sin(angle)])
vec_z = np.array([0, 1])
return_coord = x * vec_x + y * vec_y + z * vec_z
return return_coord.tolist()
pos = dict([(index, indextocoord_3d(index, size, angle=pi / 4)) for index in range(np.prod(size))])
cubic_lattice.draw(style=LatticeDrawStyle(pos=pos))
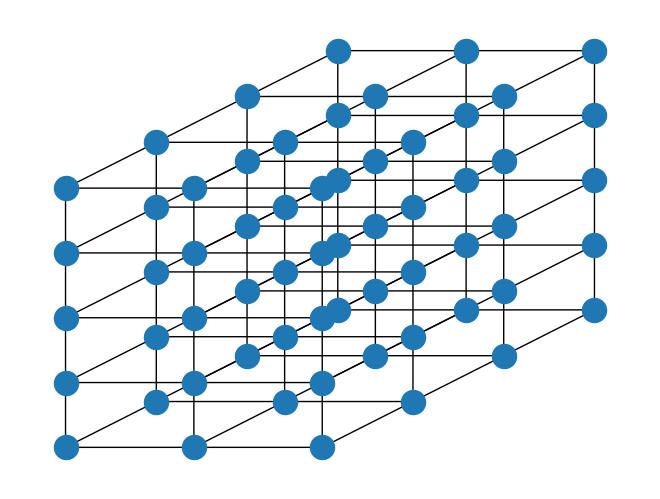
TriangularLattice#
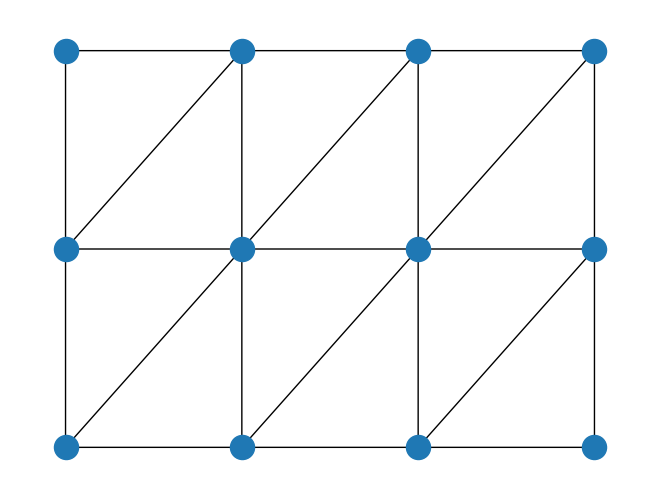
TriangularLattice provides a triangular lattice, which can be seen as a two-dimensional lattice with diagonal edges. The argument boundary_condition can take either "open" or "periodic".
[14]:
rows = 4
cols = 3
boundary_condition = BoundaryCondition.OPEN
triangular_lattice = TriangularLattice(rows=rows, cols=cols, boundary_condition=boundary_condition)
triangular_lattice.draw()
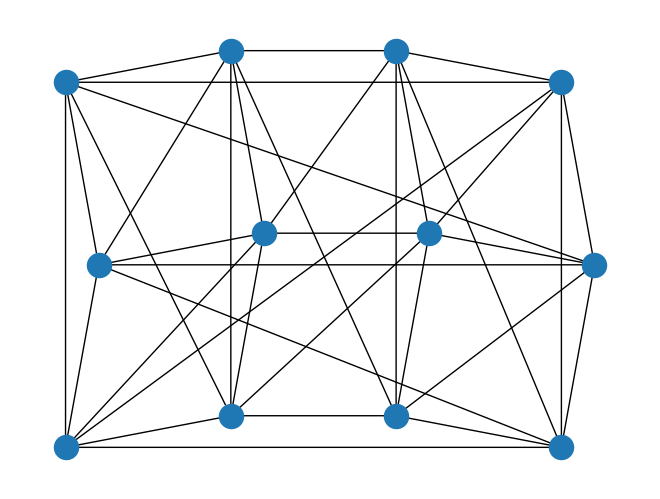
[15]:
rows = 4
cols = 3
boundary_condition = BoundaryCondition.PERIODIC
triangular_lattice = TriangularLattice(rows=rows, cols=cols, boundary_condition=boundary_condition)
triangular_lattice.draw()
General Lattice#
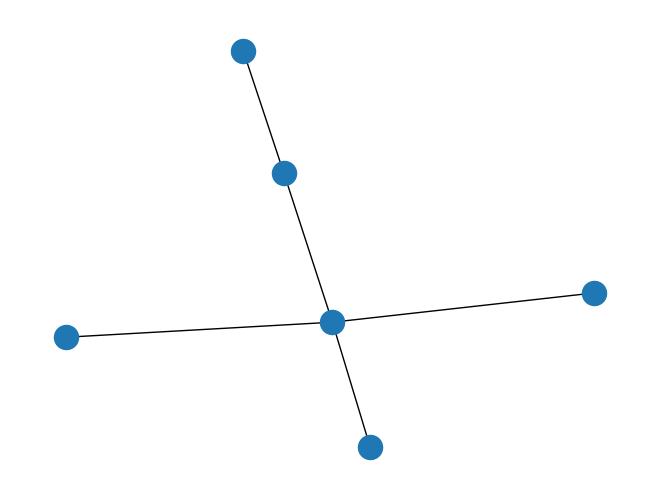
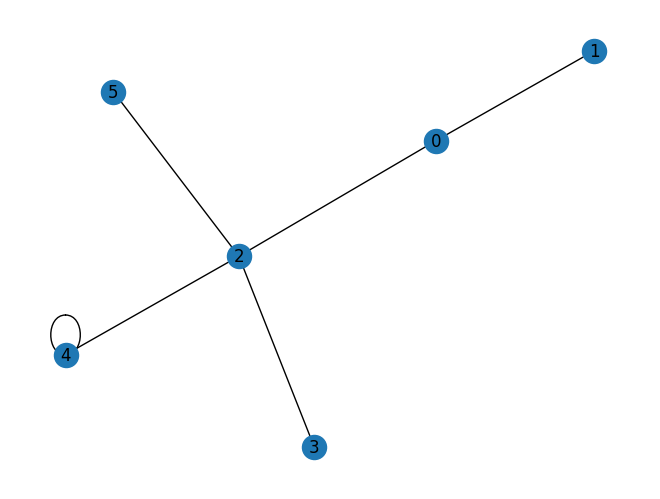
Above, we have seen translational invariant lattices. Here, we consider a general lattice. We can construct a general lattice consisting of nodes and edges using an instance of PyGraph.
[16]:
graph = rx.PyGraph(multigraph=False) # multigraph shoud be False
graph.add_nodes_from(range(6))
weighted_edge_list = [
(0, 1, 1.0 + 1.0j),
(0, 2, -1.0),
(2, 3, 2.0),
(4, 2, -1.0 + 2.0j),
(4, 4, 3.0),
(2, 5, -1.0),
]
graph.add_edges_from(weighted_edge_list)
# make a lattice
general_lattice = Lattice(graph)
set(general_lattice.graph.weighted_edge_list())
[16]:
{(0, 1, (1+1j)),
(0, 2, -1.0),
(2, 3, 2.0),
(2, 5, -1.0),
(4, 2, (-1+2j)),
(4, 4, 3.0)}
Here is its visualization.
[17]:
general_lattice.draw()
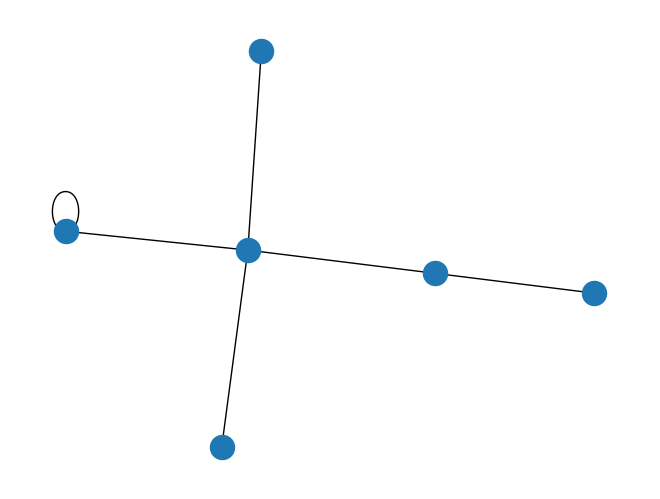
When we want to visualize the self-loops in the lattice, we set self_loop to True.
[18]:
general_lattice.draw(self_loop=True)
The labels of the lattice sites are drawn when with_labels is True.
[19]:
general_lattice.draw(self_loop=True, style=LatticeDrawStyle(with_labels=True))
The Fermi-Hubbard model#
The Fermi-Hubbard model is the simplest model describing electrons moving on a lattice and interaction with each other at the same site. The Hamiltonian is given as follows:
where \(c_{i, \sigma}^\dagger\) and \(c_{i, \sigma}\) are creation and annihilation operators of fermion at the site \(i\) with spin \(\sigma\). The operator \(n_{i, \sigma}\) is the number operator, which is defined by \(n_{i, \sigma} = c_{i, \sigma}^\dagger c_{i, \sigma}\). The matrix \(t_{i, j}\) is a Hermitian matrix called interaction matrix. The parameter \(U\) represents the strength of the interaction.
We can generate the corresponding Hamiltonian of a given lattice using FermiHubbardModel class. Here, we construct the Hamiltonian with uniform interaction and interaction parameters on a two-dimensional lattice.
[20]:
square_lattice = SquareLattice(rows=5, cols=4, boundary_condition=BoundaryCondition.PERIODIC)
t = -1.0 # the interaction parameter
v = 0.0 # the onsite potential
u = 5.0 # the interaction parameter U
fhm = FermiHubbardModel(
square_lattice.uniform_parameters(
uniform_interaction=t,
uniform_onsite_potential=v,
),
onsite_interaction=u,
)
To obtain the Hamiltonian in terms of the fermionic operators, we use second_q_ops method. The Hamiltonian is returned as an instance of FermionicOp.
Note
The number of fermionic operators required is twice the number of lattice sites because of the spin degrees of freedom.
In the implementation, even indexes correspond to up-spin and odd indexes to down-spin.
[21]:
ham = fhm.second_q_op().simplify()
print(ham)
Fermionic Operator
number spin orbitals=40, number terms=180
(-1+0j) * ( +_0 -_2 )
+ (1+0j) * ( -_0 +_2 )
+ (-1+0j) * ( +_0 -_10 )
+ (1+0j) * ( -_0 +_10 )
+ (-1+0j) * ( +_10 -_12 )
+ (1+0j) * ( -_10 +_12 )
+ (-1+0j) * ( +_10 -_20 )
+ (1+0j) * ( -_10 +_20 )
+ (-1+0j) * ( +_20 -_22 )
+ (1+0j) * ( -_20 +_22 )
+ (-1+0j) * ( +_20 -_30 )
+ (1+0j) * ( -_20 +_30 )
+ (-1+0j) * ( +_30 -_32 )
+ (1+0j) * ( -_30 +_32 )
+ (-1+0j) * ( +_2 -_4 )
+ (1+0j) * ( -_2 +_4 )
+ (-1+0j) * ( +_2 -_12 )
+ (1+0j) * ( -_2 +_12 )
+ (-1+0j) * ( +_12 -_14 )
+ (1+0j) * ( -_12 +_14 )
+ (-1+0j) * ( +_12 -_22 )
+ (1+0j) * ( -_12 +_22 )
+ (-1+0j) * ( +_22 -_24 )
+ (1+0j) * ( -_22 +_24 )
+ (-1+0j) * ( +_22 -_32 )
+ (1+0j) * ( -_22 +_32 )
+ (-1+0j) * ( +_32 -_34 )
+ (1+0j) * ( -_32 +_34 )
+ (-1+0j) * ( +_4 -_6 )
+ (1+0j) * ( -_4 +_6 )
+ (-1+0j) * ( +_4 -_14 )
+ (1+0j) * ( -_4 +_14 )
+ (-1+0j) * ( +_14 -_16 )
+ (1+0j) * ( -_14 +_16 )
+ (-1+0j) * ( +_14 -_24 )
+ (1+0j) * ( -_14 +_24 )
+ (-1+0j) * ( +_24 -_26 )
+ (1+0j) * ( -_24 +_26 )
+ (-1+0j) * ( +_24 -_34 )
+ (1+0j) * ( -_24 +_34 )
+ (-1+0j) * ( +_34 -_36 )
+ (1+0j) * ( -_34 +_36 )
+ (-1+0j) * ( +_6 -_8 )
+ (1+0j) * ( -_6 +_8 )
+ (-1+0j) * ( +_6 -_16 )
+ (1+0j) * ( -_6 +_16 )
+ (-1+0j) * ( +_16 -_18 )
+ (1+0j) * ( -_16 +_18 )
+ (-1+0j) * ( +_16 -_26 )
+ (1+0j) * ( -_16 +_26 )
+ (-1+0j) * ( +_26 -_28 )
+ (1+0j) * ( -_26 +_28 )
+ (-1+0j) * ( +_26 -_36 )
+ (1+0j) * ( -_26 +_36 )
+ (-1+0j) * ( +_36 -_38 )
+ (1+0j) * ( -_36 +_38 )
+ (-1+0j) * ( +_8 -_18 )
+ (1+0j) * ( -_8 +_18 )
+ (-1+0j) * ( +_18 -_28 )
+ (1+0j) * ( -_18 +_28 )
+ (-1+0j) * ( +_28 -_38 )
+ (1+0j) * ( -_28 +_38 )
+ (-1+0j) * ( +_0 -_8 )
+ (1+0j) * ( -_0 +_8 )
+ (-1+0j) * ( +_10 -_18 )
+ (1+0j) * ( -_10 +_18 )
+ (-1+0j) * ( +_20 -_28 )
+ (1+0j) * ( -_20 +_28 )
+ (-1+0j) * ( +_30 -_38 )
+ (1+0j) * ( -_30 +_38 )
+ (-1+0j) * ( +_0 -_30 )
+ (1+0j) * ( -_0 +_30 )
+ (-1+0j) * ( +_2 -_32 )
+ (1+0j) * ( -_2 +_32 )
+ (-1+0j) * ( +_4 -_34 )
+ (1+0j) * ( -_4 +_34 )
+ (-1+0j) * ( +_6 -_36 )
+ (1+0j) * ( -_6 +_36 )
+ (-1+0j) * ( +_8 -_38 )
+ (1+0j) * ( -_8 +_38 )
+ (-1+0j) * ( +_1 -_3 )
+ (1+0j) * ( -_1 +_3 )
+ (-1+0j) * ( +_1 -_11 )
+ (1+0j) * ( -_1 +_11 )
+ (-1+0j) * ( +_11 -_13 )
+ (1+0j) * ( -_11 +_13 )
+ (-1+0j) * ( +_11 -_21 )
+ (1+0j) * ( -_11 +_21 )
+ (-1+0j) * ( +_21 -_23 )
+ (1+0j) * ( -_21 +_23 )
+ (-1+0j) * ( +_21 -_31 )
+ (1+0j) * ( -_21 +_31 )
+ (-1+0j) * ( +_31 -_33 )
+ (1+0j) * ( -_31 +_33 )
+ (-1+0j) * ( +_3 -_5 )
+ (1+0j) * ( -_3 +_5 )
+ (-1+0j) * ( +_3 -_13 )
+ (1+0j) * ( -_3 +_13 )
+ (-1+0j) * ( +_13 -_15 )
+ (1+0j) * ( -_13 +_15 )
+ (-1+0j) * ( +_13 -_23 )
+ (1+0j) * ( -_13 +_23 )
+ (-1+0j) * ( +_23 -_25 )
+ (1+0j) * ( -_23 +_25 )
+ (-1+0j) * ( +_23 -_33 )
+ (1+0j) * ( -_23 +_33 )
+ (-1+0j) * ( +_33 -_35 )
+ (1+0j) * ( -_33 +_35 )
+ (-1+0j) * ( +_5 -_7 )
+ (1+0j) * ( -_5 +_7 )
+ (-1+0j) * ( +_5 -_15 )
+ (1+0j) * ( -_5 +_15 )
+ (-1+0j) * ( +_15 -_17 )
+ (1+0j) * ( -_15 +_17 )
+ (-1+0j) * ( +_15 -_25 )
+ (1+0j) * ( -_15 +_25 )
+ (-1+0j) * ( +_25 -_27 )
+ (1+0j) * ( -_25 +_27 )
+ (-1+0j) * ( +_25 -_35 )
+ (1+0j) * ( -_25 +_35 )
+ (-1+0j) * ( +_35 -_37 )
+ (1+0j) * ( -_35 +_37 )
+ (-1+0j) * ( +_7 -_9 )
+ (1+0j) * ( -_7 +_9 )
+ (-1+0j) * ( +_7 -_17 )
+ (1+0j) * ( -_7 +_17 )
+ (-1+0j) * ( +_17 -_19 )
+ (1+0j) * ( -_17 +_19 )
+ (-1+0j) * ( +_17 -_27 )
+ (1+0j) * ( -_17 +_27 )
+ (-1+0j) * ( +_27 -_29 )
+ (1+0j) * ( -_27 +_29 )
+ (-1+0j) * ( +_27 -_37 )
+ (1+0j) * ( -_27 +_37 )
+ (-1+0j) * ( +_37 -_39 )
+ (1+0j) * ( -_37 +_39 )
+ (-1+0j) * ( +_9 -_19 )
+ (1+0j) * ( -_9 +_19 )
+ (-1+0j) * ( +_19 -_29 )
+ (1+0j) * ( -_19 +_29 )
+ (-1+0j) * ( +_29 -_39 )
+ (1+0j) * ( -_29 +_39 )
+ (-1+0j) * ( +_1 -_9 )
+ (1+0j) * ( -_1 +_9 )
+ (-1+0j) * ( +_11 -_19 )
+ (1+0j) * ( -_11 +_19 )
+ (-1+0j) * ( +_21 -_29 )
+ (1+0j) * ( -_21 +_29 )
+ (-1+0j) * ( +_31 -_39 )
+ (1+0j) * ( -_31 +_39 )
+ (-1+0j) * ( +_1 -_31 )
+ (1+0j) * ( -_1 +_31 )
+ (-1+0j) * ( +_3 -_33 )
+ (1+0j) * ( -_3 +_33 )
+ (-1+0j) * ( +_5 -_35 )
+ (1+0j) * ( -_5 +_35 )
+ (-1+0j) * ( +_7 -_37 )
+ (1+0j) * ( -_7 +_37 )
+ (-1+0j) * ( +_9 -_39 )
+ (1+0j) * ( -_9 +_39 )
+ (5+0j) * ( +_0 -_0 +_1 -_1 )
+ (5+0j) * ( +_2 -_2 +_3 -_3 )
+ (5+0j) * ( +_4 -_4 +_5 -_5 )
+ (5+0j) * ( +_6 -_6 +_7 -_7 )
+ (5+0j) * ( +_8 -_8 +_9 -_9 )
+ (5+0j) * ( +_10 -_10 +_11 -_11 )
+ (5+0j) * ( +_12 -_12 +_13 -_13 )
+ (5+0j) * ( +_14 -_14 +_15 -_15 )
+ (5+0j) * ( +_16 -_16 +_17 -_17 )
+ (5+0j) * ( +_18 -_18 +_19 -_19 )
+ (5+0j) * ( +_20 -_20 +_21 -_21 )
+ (5+0j) * ( +_22 -_22 +_23 -_23 )
+ (5+0j) * ( +_24 -_24 +_25 -_25 )
+ (5+0j) * ( +_26 -_26 +_27 -_27 )
+ (5+0j) * ( +_28 -_28 +_29 -_29 )
+ (5+0j) * ( +_30 -_30 +_31 -_31 )
+ (5+0j) * ( +_32 -_32 +_33 -_33 )
+ (5+0j) * ( +_34 -_34 +_35 -_35 )
+ (5+0j) * ( +_36 -_36 +_37 -_37 )
+ (5+0j) * ( +_38 -_38 +_39 -_39 )
Lattice has weights on its edges, so we can define a general interaction matrix using a Lattice instance. Here, we consider the Fermi-Hubbard model on a general lattice on which non-uniform interaction parameters are given. In this case, the weights of the lattice are regarded as the interaction matrix. After generating the Hamiltonian (second_q_ops) we can use a qubit mapper to generate the qubit operators and/or use any of the available algorithms to solver the corresponding lattice
problem.
[22]:
graph = rx.PyGraph(multigraph=False) # multiigraph shoud be False
graph.add_nodes_from(range(6))
weighted_edge_list = [
(0, 1, 1.0 + 1.0j),
(0, 2, -1.0),
(2, 3, 2.0),
(4, 2, -1.0 + 2.0j),
(4, 4, 3.0),
(2, 5, -1.0),
]
graph.add_edges_from(weighted_edge_list)
general_lattice = Lattice(graph) # the lattice whose weights are seen as the interaction matrix.
u = 5.0 # the interaction parameter U
fhm = FermiHubbardModel(lattice=general_lattice, onsite_interaction=u)
ham = fhm.second_q_op().simplify()
print(ham)
Fermionic Operator
number spin orbitals=12, number terms=28
(1+1j) * ( +_0 -_2 )
+ (-1+1j) * ( -_0 +_2 )
+ (-1+0j) * ( +_0 -_4 )
+ (1+0j) * ( -_0 +_4 )
+ (2+0j) * ( +_4 -_6 )
+ (-2+0j) * ( -_4 +_6 )
+ (-1-2j) * ( +_4 -_8 )
+ (1-2j) * ( -_4 +_8 )
+ (3+0j) * ( +_8 -_8 )
+ (-1+0j) * ( +_4 -_10 )
+ (1+0j) * ( -_4 +_10 )
+ (1+1j) * ( +_1 -_3 )
+ (-1+1j) * ( -_1 +_3 )
+ (-1+0j) * ( +_1 -_5 )
+ (1+0j) * ( -_1 +_5 )
+ (2+0j) * ( +_5 -_7 )
+ (-2+0j) * ( -_5 +_7 )
+ (-1-2j) * ( +_5 -_9 )
+ (1-2j) * ( -_5 +_9 )
+ (3+0j) * ( +_9 -_9 )
+ (-1+0j) * ( +_5 -_11 )
+ (1+0j) * ( -_5 +_11 )
+ (5+0j) * ( +_0 -_0 +_1 -_1 )
+ (5+0j) * ( +_2 -_2 +_3 -_3 )
+ (5+0j) * ( +_4 -_4 +_5 -_5 )
+ (5+0j) * ( +_6 -_6 +_7 -_7 )
+ (5+0j) * ( +_8 -_8 +_9 -_9 )
+ (5+0j) * ( +_10 -_10 +_11 -_11 )
LatticeModelProblem#
Qiskit Nature also has a LatticeModelProblem class which allows the usage of the GroundStateEigensolver to calculate the ground state energy of a given lattice. You can use this class as follows:
[23]:
from qiskit_nature.second_q.problems import LatticeModelProblem
num_nodes = 4
boundary_condition = BoundaryCondition.OPEN
line_lattice = LineLattice(num_nodes=num_nodes, boundary_condition=boundary_condition)
fhm = FermiHubbardModel(
line_lattice.uniform_parameters(
uniform_interaction=t,
uniform_onsite_potential=v,
),
onsite_interaction=u,
)
lmp = LatticeModelProblem(fhm)
[24]:
from qiskit_algorithms import NumPyMinimumEigensolver
from qiskit_nature.second_q.algorithms import GroundStateEigensolver
from qiskit_nature.second_q.mappers import JordanWignerMapper
numpy_solver = NumPyMinimumEigensolver()
qubit_mapper = JordanWignerMapper()
calc = GroundStateEigensolver(qubit_mapper, numpy_solver)
res = calc.solve(lmp)
print(res)
=== GROUND STATE ===
* Lattice ground state energy : -2.566350190841
[25]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.24.0.dev0+2b3686f |
qiskit-aer | 0.11.2 |
qiskit-ibmq-provider | 0.19.2 |
qiskit-nature | 0.6.0 |
| System information | |
| Python version | 3.9.16 |
| Python compiler | GCC 12.2.1 20221121 (Red Hat 12.2.1-4) |
| Python build | main, Dec 7 2022 00:00:00 |
| OS | Linux |
| CPUs | 8 |
| Memory (Gb) | 62.50002670288086 |
| Thu Apr 06 09:13:58 2023 CEST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.