Nota

Esta página fue generada a partir de docs/tutorials/07_leveraging_qiskit_runtime.ipynb.

Aprovechando Qiskit Runtime#

Advertencia

El VQEClient discutido en este tutorial está OBSOLETO a partir de la versión 0.6 de Qiskit Nature y se eliminará no antes de los 3 meses posteriores a la liberación. En su lugar, debes utilizar el nuevo VQE basado en primitivas con la primitiva Estimator de Qiskit IBM Runtime. Para obtener más detalles sobre cómo migrar, consulta esta guía aquí.

Los algoritmos iterativos, como el Solucionador Propio Variacional Cuántico (Variational Quantum Eigensolver, VQE), tradicionalmente envían un lote de circuitos (un «trabajo» o «job») para ser ejecutados en el dispositivo cuántico en cada iteración. Mandar un trabajo implica una cierta sobrecarga, principalmente

el tiempo para procesar las solicitudes y enviar los datos (sobrecarga de API, generalmente alrededor de 10s)
el tiempo de espera del trabajo, es decir, cuánto tienes que esperar antes que sea tu turno de ejecutar en el dispositivo (por lo general unos 2min)

Si enviamos cientos de trabajos iterativamente, esta sobrecarga rápidamente domina el tiempo de ejecución de nuestro algoritmo. Qiskit Runtime nos permite abordar estos problemas y significativamente acelerar (especialmente) algoritmos iterativos. Con Qiskit Runtime, un trabajo no contiene solo un lote de circuitos, sino el algoritmo entero. ¡Esto significa que solamente experimentamos la sobrecarga de la API y el tiempo de espera una vez en lugar de en cada iteración! Podrás cargar parámetros para el algoritmo y delegar toda la complejidad a la nube, donde tu programa es ejecutado, o directamente cargar tu propio algoritmo.

Para el VQE, la integración de Qiskit Runtime en tu código existente es pan comido. Hay un (casi) reemplazo directo, llamado VQEClient para la clase VQE.

Veamos como puedes aprovechar el runtime en un ejemplo simple de química: Encontrar la energía del estado fundamental de la molécula de hidrato de litio (LiH) a una distancia de enlace dada.

Especificación del problema: molécula de LiH#

En primer lugar, especificamos la molécula de la cual buscamos su energía del estado fundamental. Aquí, trabajamos con LiH con una distancia de enlace de 2.5 Å.

[1]:

from qiskit_nature.units import DistanceUnit
from qiskit_nature.second_q.drivers import PySCFDriver
from qiskit_nature.second_q.mappers import ParityMapper
from qiskit_nature.second_q.properties import ParticleNumber
from qiskit_nature.second_q.transformers import ActiveSpaceTransformer

[2]:

bond_distance = 2.5  # in Angstrom

# specify driver
driver = PySCFDriver(
    atom=f"Li 0 0 0; H 0 0 {bond_distance}",
    basis="sto3g",
    charge=0,
    spin=0,
    unit=DistanceUnit.ANGSTROM,
)
problem = driver.run()

# specify active space transformation
active_space_trafo = ActiveSpaceTransformer(
    num_electrons=problem.num_particles, num_spatial_orbitals=3
)

# transform the electronic structure problem
problem = active_space_trafo.transform(problem)

# construct the parity mapper with 2-qubit reduction
qubit_mapper = ParityMapper(num_particles=problem.num_particles)

Solución clásica de referencia#

Como solución de referencia podemos resolver este sistema clásicamente con el NumPyEigensolver.

[3]:

from qiskit_algorithms import NumPyMinimumEigensolver
from qiskit_nature.second_q.algorithms.ground_state_solvers import GroundStateEigensolver

np_solver = NumPyMinimumEigensolver()
np_groundstate_solver = GroundStateEigensolver(qubit_mapper, np_solver)

np_result = np_groundstate_solver.solve(problem)

[19]:

target_energy = np_result.total_energies[0]
print(np_result)

=== GROUND STATE ENERGY ===

* Electronic ground state energy (Hartree): -8.408630641972
  - computed part:      -8.408630641972
  - ActiveSpaceTransformer extracted energy part: 0.0
~ Nuclear repulsion energy (Hartree): 0.635012653104
> Total ground state energy (Hartree): -7.773617988868

=== MEASURED OBSERVABLES ===

  0:  # Particles: 4.000 S: 0.000 S^2: 0.000 M: 0.000

=== DIPOLE MOMENTS ===

~ Nuclear dipole moment (a.u.): [0.0  0.0  4.72431531]

  0:
  * Electronic dipole moment (a.u.): [0.0  0.0  6.45025807]
    - computed part:      [0.0  0.0  6.45025807]
    - ActiveSpaceTransformer extracted energy part: [0.0  0.0  0.0]
  > Dipole moment (a.u.): [0.0  0.0  -1.72594276]  Total: 1.72594276
                 (debye): [0.0  0.0  -4.38690851]  Total: 4.38690851

VQE#

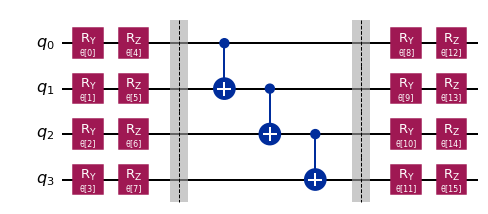
Para ejecutar el VQE tenemos que seleccionar un circuito cuántico parametrizado que actúe como ansatz y un optimizador clásico. Aquí escogeremos un ansatz heurístico, eficiente en hardware y el optimizador SPSA.

[5]:

from qiskit.circuit.library import EfficientSU2

ansatz = EfficientSU2(num_qubits=4, reps=1, entanglement="linear", insert_barriers=True)
ansatz.decompose().draw("mpl", style="iqx")

[5]:

../_images/tutorials_07_leveraging_qiskit_runtime_11_0.png

[6]:

import numpy as np
from qiskit.utils import algorithm_globals

# fix random seeds for reproducibility

np.random.seed(5)
algorithm_globals.random_seed = 5

[7]:

from qiskit_algorithms.optimizers import SPSA

optimizer = SPSA(maxiter=100)

initial_point = np.random.random(ansatz.num_parameters)

Antes de ejecutar el VQE en la nube usando Qiskit Runtime, ejecutemos primero un VQE local.

[8]:

from qiskit_algorithms import VQE
from qiskit.primitives import Estimator

estimator = Estimator()

local_vqe = VQE(
    estimator,
    ansatz,
    optimizer,
    initial_point=initial_point,
)

local_vqe_groundstate_solver = GroundStateEigensolver(qubit_mapper, local_vqe)

local_vqe_result = local_vqe_groundstate_solver.solve(problem)

[9]:

print(local_vqe_result)

=== GROUND STATE ENERGY ===

* Electronic ground state energy (Hartree): -8.223473551005
  - computed part:      -8.223473551005
  - ActiveSpaceTransformer extracted energy part: 0.0
~ Nuclear repulsion energy (Hartree): 0.635012653104
> Total ground state energy (Hartree): -7.588460897901

=== MEASURED OBSERVABLES ===

  0:  # Particles: 3.997 S: 0.438 S^2: 0.631 M: 0.001

=== DIPOLE MOMENTS ===

~ Nuclear dipole moment (a.u.): [0.0  0.0  4.72431531]

  0:
  * Electronic dipole moment (a.u.): [0.0  0.0  1.41136787]
    - computed part:      [0.0  0.0  1.41136787]
    - ActiveSpaceTransformer extracted energy part: [0.0  0.0  0.0]
  > Dipole moment (a.u.): [0.0  0.0  3.31294744]  Total: 3.31294744
                 (debye): [0.0  0.0  8.42067168]  Total: 8.42067168

VQE de Runtime#

Cambiemos el solucionador propio de un algoritmo VQE local a un VQE ejecutado usando Qiskit Runtime, simplemente intercambiando la clase VQE por el qiskit_nature.runtime.VQEClient.

Primero, tendremos que cargar un proveedor para acceder a Qiskit Runtime. Nota: Tienes que reemplazar la siguiente celda con tu proveedor.

[10]:

from qiskit import IBMQ

IBMQ.load_account()
provider = IBMQ.get_provider(group="open")  # replace by your runtime provider

backend = provider.get_backend("ibmq_qasm_simulator")  # select a backend that supports the runtime

Ahora podemos configurar el VQEClient. En esta primera versión, el optimizador debe proporcionarse como un diccionario; en versiones futuras, podrás pasar el mismo objeto optimizador que en el VQE tradicional.

[11]:

from qiskit_nature.runtime import VQEClient

runtime_vqe = VQEClient(
    ansatz=ansatz,
    optimizer=optimizer,
    initial_point=initial_point,
    provider=provider,
    backend=backend,
    shots=1024,
    measurement_error_mitigation=True,
)  # use a complete measurement fitter for error mitigation

[12]:

runtime_vqe_groundstate_solver = GroundStateEigensolver(qubit_mapper, runtime_vqe)
runtime_vqe_result = runtime_vqe_groundstate_solver.solve(problem)

[13]:

print(runtime_vqe_result)

=== GROUND STATE ENERGY ===

* Electronic ground state energy (Hartree): -8.172591259069
  - computed part:      -8.172591259069
  - ActiveSpaceTransformer extracted energy part: 0.0
~ Nuclear repulsion energy (Hartree): 0.635012653104
> Total ground state energy (Hartree): -7.537578605965

=== MEASURED OBSERVABLES ===

  0:  # Particles: 3.988 S: 0.596 S^2: 0.951 M: 0.002

=== DIPOLE MOMENTS ===

~ Nuclear dipole moment (a.u.): [0.0  0.0  4.72431531]

  0:
  * Electronic dipole moment (a.u.): [0.0  0.0  1.25645131]
    - computed part:      [0.0  0.0  1.25645131]
    - ActiveSpaceTransformer extracted energy part: [0.0  0.0  0.0]
  > Dipole moment (a.u.): [0.0  0.0  3.467864]  Total: 3.467864
                 (debye): [0.0  0.0  8.81443024]  Total: 8.81443024

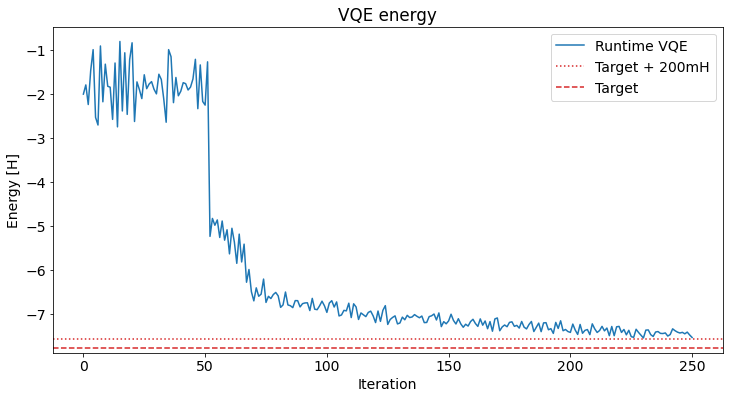
Si estamos interesados en el desarrollo de la energía, el VQEClient permite acceder al historial del optimizador, que contiene la pérdida por iteración (junto con los parámetros y una marca de tiempo). Ten en cuenta que esto solo es válido para los optimizadores SPSA y QN-SPSA. De lo contrario, debes usar una devolución de llamada (callback) al VQEClient, similar al VQE normal.

Podemos acceder a estos datos a través del atributo raw_result del solucionador de estado fundamental.

[17]:

runtime_result = runtime_vqe_result.raw_result
history = runtime_result.optimizer_history
loss = history["energy"]

[20]:

import matplotlib.pyplot as plt

plt.rcParams["font.size"] = 14

# plot loss and reference value
plt.figure(figsize=(12, 6))
plt.plot(loss + runtime_vqe_result.nuclear_repulsion_energy, label="Runtime VQE")
plt.axhline(y=target_energy + 0.2, color="tab:red", ls=":", label="Target + 200mH")
plt.axhline(y=target_energy, color="tab:red", ls="--", label="Target")

plt.legend(loc="best")
plt.xlabel("Iteration")
plt.ylabel("Energy [H]")
plt.title("VQE energy");

../_images/tutorials_07_leveraging_qiskit_runtime_25_0.png

[21]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
`qiskit-terra`	0.23.0.dev0+f339f71
`qiskit-aer`	0.11.1
`qiskit-ibmq-provider`	0.19.2
`qiskit-nature`	0.6.0
System information
Python version	3.9.15
Python compiler	GCC 12.2.1 20220819 (Red Hat 12.2.1-2)
Python build	main, Oct 12 2022 00:00:00
OS	Linux
CPUs	8
Memory (Gb)	62.499855041503906
Wed Dec 07 11:09:57 2022 CET

This code is a part of Qiskit

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.