Nota
Esta página fue generada a partir de docs/tutorials/06_qubit_mappers.ipynb.
Mapear al Espacio de Qubit#
Los problemas y operadores con los que interactúas en Qiskit Nature (por lo general) deben mapearse al espacio de qubits antes de que puedan resolverse con nuestros algoritmos cuánticos. Esta tarea es manejada por varias clases QubitMapper.
En este tutorial, aprenderás acerca de las diversas opciones disponibles para ti.
Mapeadores Fermiónicos#
Esta sección trata sobre mapeadores fermiónicos, que transforman operadores fermiónicos en el espacio de qubits. Esto es utilizado principalmente por la pila de estructura electrónica, pero también encuentra aplicación para el `FermiHubbardModel <TODO>`__.
Existen diferentes tipos de mapeo con diferentes propiedades. Qiskit Nature ya admite los siguientes mapeos fermiónicos:
Jordan-Wigner (Zeitschrift für Physik, 47, 631-651 (1928))
Parity (The Journal of chemical physics, 137(22), 224109 (2012))
Bravyi-Kitaev (Annals of Physics, 298(1), 210-226 (2002))
Discutiremos algunos de estos en las siguientes secciones. Debes aprender toda la información necesaria para trabajar cómodamente con cualquiera de los mapeadores disponibles.
Para discutir los diversos mapeos, usaremos el Hamiltoniano de la estructura electrónica de la molécula H2. Para obtener más información sobre cómo obtener esto, consulta el tutorial de estructura electrónica.
[1]:
from qiskit_nature.second_q.drivers import PySCFDriver
driver = PySCFDriver()
problem = driver.run()
fermionic_op = problem.hamiltonian.second_q_op()
El Mapeo de Jordan-Wigner#
El mapeo de Jordan-Wigner es el mapeo más directo con la interpretación física más simple, porque mapea la ocupación de un orbital de espín a la ocupación de un qubit.
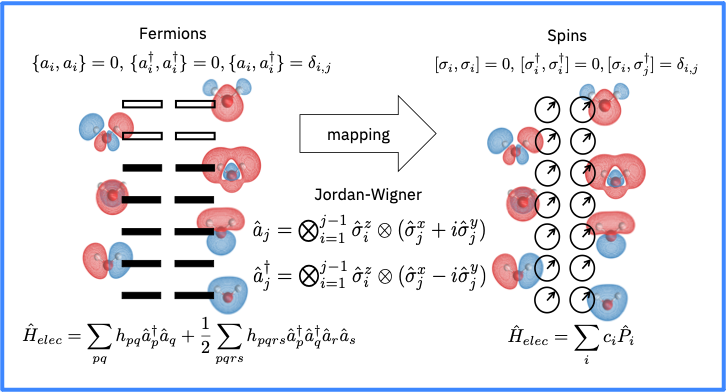
Puedes construirlo así:
[2]:
from qiskit_nature.second_q.mappers import JordanWignerMapper
mapper = JordanWignerMapper()
[3]:
qubit_jw_op = mapper.map(fermionic_op)
print(qubit_jw_op)
-0.8105479805373283 * IIII
+ 0.17218393261915543 * IIIZ
- 0.2257534922240237 * IIZI
+ 0.12091263261776633 * IIZZ
+ 0.17218393261915543 * IZII
+ 0.16892753870087907 * IZIZ
+ 0.045232799946057826 * YYYY
+ 0.045232799946057826 * XXYY
+ 0.045232799946057826 * YYXX
+ 0.045232799946057826 * XXXX
- 0.22575349222402363 * ZIII
+ 0.1661454325638241 * ZIIZ
+ 0.16614543256382408 * IZZI
+ 0.1746434306830045 * ZIZI
+ 0.12091263261776633 * ZZII
True
El Mapeo de Paridad#
El mapeo de Paridad (parity) es el mapeo dual del de Jordan-Wigner, en el sentido de que codifica la información de paridad localmente en un qubit, mientras que la información de ocupación se deslocaliza en todos los qubits.
[4]:
from qiskit_nature.second_q.mappers import ParityMapper
mapper = ParityMapper()
[5]:
qubit_p_op = mapper.map(fermionic_op)
print(qubit_p_op)
-0.8105479805373283 * IIII
+ 0.17218393261915543 * IIIZ
- 0.2257534922240237 * IIZZ
+ 0.12091263261776633 * IIZI
+ 0.17218393261915543 * IZZI
+ 0.16892753870087907 * IZZZ
+ 0.045232799946057826 * ZXIX
- 0.045232799946057826 * IXZX
- 0.045232799946057826 * ZXZX
+ 0.045232799946057826 * IXIX
- 0.22575349222402363 * ZZII
+ 0.1661454325638241 * ZZIZ
+ 0.16614543256382408 * IZIZ
+ 0.1746434306830045 * ZZZZ
+ 0.12091263261776633 * ZIZI
Esto tiene un gran beneficio para el caso de problemas en los que queremos preservar el número de partículas de cada especie de espín; nos permite eliminar 2 qubits, porque la información en ellos se vuelve redundante. Dado que Qiskit Nature organiza los qubits en orden de bloque, de modo que la primera mitad codifica el espín alfa y la segunda mitad la información del espín beta, esto significa que podemos eliminar el N/2-ésimo y N-ésimo qubit.
Para hacer esto, debes especificar el número de partículas en tu sistema, así:
[6]:
mapper = ParityMapper(num_particles=problem.num_particles)
[7]:
qubit_op = mapper.map(fermionic_op)
print(qubit_op)
-1.0523732457728605 * II
+ 0.39793742484317896 * IZ
- 0.39793742484317896 * ZI
- 0.01128010425623538 * ZZ
+ 0.18093119978423122 * XX
Reducciones de qubits más avanzadas#
También es posible realizar reducciones de qubits más avanzadas, que se basan en encontrar simetrías Z2 en el espacio de Hilbert del qubit. Un requisito para que esto sea útil es que sepas en qué subespacio de simetría necesitas buscar tu solución real de interés. Esto puede ser un poco complicado, pero afortunadamente las clases de problemas de Qiskit Nature te brindan una utilidad para determinar automáticamente ese subespacio correcto.
Así es como puedes usar esto a tu favor:
[8]:
tapered_mapper = problem.get_tapered_mapper(mapper)
print(type(tapered_mapper))
<class 'qiskit_nature.second_q.mappers.tapered_qubit_mapper.TaperedQubitMapper'>
[9]:
qubit_op = tapered_mapper.map(fermionic_op)
print(qubit_op)
-1.041093141516625 * I
- 0.7958748496863577 * Z
- 0.1809311997842312 * X
¡Como puedes ver aquí, la molécula H2 es un sistema tan simple que podemos simularla completamente en un solo qubit!
Orden intercalado#
Como se mencionó anteriormente, Qiskit Nature organiza las partes fermiónicas de espín arriba y espín abajo del registro de qubit en orden de bloques. Sin embargo, a veces uno puede desear intercalar los registros en su lugar. Esto se puede lograr con InterleavedQubitMapper. Esto se puede mostrar mejor al inspeccionar el circuito del estado inicial HarteeFock:
[10]:
from qiskit_nature.second_q.circuit.library import HartreeFock
[11]:
hf_state = HartreeFock(2, (1, 1), JordanWignerMapper())
hf_state.draw()
[11]:
┌───┐
q_0: ┤ X ├
└───┘
q_1: ─────
┌───┐
q_2: ┤ X ├
└───┘
q_3: ─────
[12]:
from qiskit_nature.second_q.mappers import InterleavedQubitMapper
[13]:
interleaved_mapper = InterleavedQubitMapper(JordanWignerMapper())
[14]:
hf_state = HartreeFock(2, (1, 1), interleaved_mapper)
hf_state.draw()
[14]:
┌───┐
q_0: ┤ X ├
├───┤
q_1: ┤ X ├
└───┘
q_2: ─────
q_3: ─────
[15]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.24.0.dev0+2b3686f |
qiskit-aer | 0.11.2 |
qiskit-ibmq-provider | 0.19.2 |
qiskit-nature | 0.6.0 |
| System information | |
| Python version | 3.9.16 |
| Python compiler | GCC 12.2.1 20221121 (Red Hat 12.2.1-4) |
| Python build | main, Dec 7 2022 00:00:00 |
| OS | Linux |
| CPUs | 8 |
| Memory (Gb) | 62.50002670288086 |
| Thu Apr 06 09:11:44 2023 CEST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.