Nota

Esta página fue generada a partir de docs/tutorials/12_deuteron_binding_energy.ipynb.

Energía de Enlace entre el protón y el neutrón en el núcleo del Deuterón#

En la etapa actual de la computación cuántica, los procesadores cuánticos que tenemos disponibles aún no tienen códigos de corrección de errores implementados y, por lo tanto, todavía tienen ruido con el que deben lidiar. Este ruido puede afectar negativamente a los resultados y, en consecuencia, puede limitar el tipo de problemas que podemos abordar actualmente cuando, debido al ruido, no se puede esperar un alto nivel de confianza y precisión de los resultados.

Sin embargo, hay algunos problemas que requieren solo unos pocos qubits para ser resueltos, como el cálculo de la energía de enlace entre el protón y el neutrón en el núcleo del Deuterón [1]. Este problema es un ejemplo de un escenario en el que podemos lograr buenos resultados a pesar de los desafíos mencionados anteriormente.

Paso 1: Importar de los paquetes que necesitamos para abordar el problema#

[1]:

import numpy as np
import matplotlib.pyplot as plt
from IPython.display import display, clear_output
from qiskit.primitives import Estimator
from qiskit_algorithms import VQE
from qiskit_algorithms.observables_evaluator import estimate_observables
from qiskit_algorithms.optimizers import COBYLA, SLSQP
from qiskit.circuit import QuantumCircuit, Parameter
from qiskit.circuit.library import TwoLocal
from qiskit.quantum_info import Pauli, SparsePauliOp
from qiskit.utils import algorithm_globals
from qiskit_nature.second_q.operators import FermionicOp
from qiskit_nature.second_q.mappers import JordanWignerMapper

Paso 2: Definir algunas funciones que usaremos#

Antes de comenzar la definición del Hamiltoniano del Deuterón, debemos definir una función de utilidad que implemente la delta de Kronecker, que se define de la siguiente manera:

\(\delta_{n,m} = \bigg\{\begin{array}{c}0, \ \textrm{si} \ n \neq m \\1, \ \textrm{si } \ n = m.\end{array}\).

Esta función aparece en la definición del Hamiltoniano del Deuterón dada en [1]. A continuación tenemos un fragmento de código que define la función de la delta de Kronecker.

[2]:

def kronecker_delta_function(n: int, m: int) -> int:
    """An implementation of the Kronecker delta function.

    Args:
        n (int): The first integer argument.
        m (int): The second integer argument.

    Returns:
        Returns 1 if n = m, else returns 0.
    """
    return int(n == m)

En [1] podemos encontrar la siguiente expresión para el Hamiltoniano del Deuterón \(H_N = \sum_{n,m=0}^{N-1}\langle m|(T+V)|n\rangle a_{m}^\dagger a_n\), donde \(|n\rangle\) y \(|m\rangle\) representan estados cuánticos en la base del oscilador armónico, y \(a_m^\dagger\) y \(a_n\) representan los operadores de creación y aniquilación, respectivamente.

Para crear el código que define a \(H_N\), necesitamos los elementos de la matriz de energía cinética y potencial. De nuevo, encontramos estas expresiones en [1]:

\(\langle m|T|n\rangle = \frac{\hbar\omega}{2}\left[\left(2n+\frac{3}{2}\right)\delta_{n,m}-\sqrt{n(n+\frac{1}{2})}\delta_{n,m+1}-\sqrt{(n+1)(n+\frac{3}{2})}\delta_{n,m-1}\right],\) \(\langle m|V|n\rangle = V_0\delta_{n,0}\delta_{n,m}.\)

Donde \(V_0 = -5.68658111 \ \textrm{MeV}\) y \(\hbar\omega = 7 \ \textrm{MeV}\). Sin embargo, el Hamiltoniano escrito de esta manera no se puede procesar directamente en una computadora cuántica, porque una computadora cuántica manipula qubits a través de compuertas basadas en matrices de Pauli. Por lo tanto, necesitamos convertir los operadores de creación y aniquilación en operadores de Pauli. Para hacer eso, podemos hacer uso de la transformación de Jordan-Wigner

\(a_n^\dagger \ \rightarrow \ \frac{1}{2}\left[\prod_{j=0}^{n-1}-Z_j\right](X_n-iY_n),\)

\(a_n \ \rightarrow \ \frac{1}{2}\left[\prod_{j=0}^{n-1}-Z_j\right](X_n+iY_n).\)

Afortunadamente, en Qiskit Nature disponemos de herramientas para definir operadores fermiónicos y convertir este tipo de operadores en operadores de Pauli mediante la transformación de Jordan-Wigner. Inicialmente, usamos un bucle for para construir y almacenar las etiquetas y los coeficientes en una tupla y, después de esto, agregamos la tupla en una lista. Cada etiqueta de cadena y cada coeficiente definen un elemento cinético \(\langle m|T|n\rangle\) y un elemento potencial \(\langle m|V|n\rangle\) del Hamiltoniano. Al final del bucle for, tenemos que pasar la lista con las tuplas con etiquetas y coeficientes a FermionicOp, para crear un Hamiltoniano en términos de los operadores de creación y aniquilación. Necesitamos reescribir este Hamiltoniano en términos de operadores de Pauli, para hacer esto usamos JordanWignerMapper(). Para obtener más información sobre las herramientas de Qiskit Nature, recomendamos leer la documentación de Qiskit Nature [2].

[3]:

def create_deuteron_hamiltonian(
    N: int, hbar_omega: float = 7.0, V_0: float = -5.68658111
) -> SparsePauliOp:
    """Creates a version of the Deuteron Hamiltonian as a qubit operator.

    Args:
        N (int): An integer number that represents the dimension of the
            basis.
        hbar_omega (float, optional): The value of the product of hbar and omega. Defaults to 7.0.
        V_0 (float, optional): The value of the potential energy. Defaults to -5.68658111.

    Returns:
        SparsePauliOp: The qubit-space Hamiltonian that represents the Deuteron.
    """
    hamiltonian_terms = {}
    for m in range(N):
        for n in range(N):

            label = "+_{} -_{}".format(str(n), str(m))
            coefficient_kinect = (hbar_omega / 2) * (
                (2 * n + 3 / 2) * kronecker_delta_function(n, m)
                - np.sqrt(n * (n + (1 / 2))) * kronecker_delta_function(n, m + 1)
                - np.sqrt((n + 1) * (n + (3 / 2)) * kronecker_delta_function(n, m - 1))
            )
            hamiltonian_terms[label] = coefficient_kinect

            coefficient_potential = (
                V_0 * kronecker_delta_function(n, 0) * kronecker_delta_function(n, m)
            )
            hamiltonian_terms[label] += coefficient_potential

    hamiltonian = FermionicOp(hamiltonian_terms, num_spin_orbitals=N)
    mapper = JordanWignerMapper()
    qubit_hamiltonian = mapper.map(hamiltonian)
    if not isinstance(qubit_hamiltonian, SparsePauliOp):
        qubit_hamiltonian = qubit_hamiltonian.primitive

    return qubit_hamiltonian

Ahora, tenemos una idea de cómo usar algunas de las herramientas de Qiskit Nature para construir un Hamiltoniano en términos de operadores de Pauli. Sin embargo, este no es el final, necesitamos construir un ansatz a través de un circuito cuántico parametrizado y usarlo en el VQE para calcular el valor propio mínimo del Hamiltoniano del Deuterón (energía de enlace).

Paso 3: Usar las herramientas de Qiskit para calcular la energía de enlace entre el protón y el neutrón en el núcleo del Deuterón#

En el paso anterior hemos definido las funciones que nos serán útiles en la tarea de calcular la energía de enlace entre el protón y el neutrón en el núcleo del Deuterón. Por lo tanto, ahora es el momento de comenzar el proceso de resolución del problema con las herramientas que construimos.

Ahora es el momento de crear el Hamiltoniano, comenzaremos con \(H_1\), que es la forma más simple del Hamiltoniano del deuterón (\(N = 1\)). En [1], los autores calcularon la energía del estado fundamental para \(N = 1,2,3\) y usaron esos valores para extrapolar la energía e intentar alcanzar \(-2.22 \ MeV\), el valor de la energía del estado fundamental del deuterón. Aquí crearemos una lista para almacenar los Hamiltonianos \(H_1\), \(H_2\), \(H_3\) y \(H_4\), porque usaremos estos Hamiltonianos más adelante para calcular el estado fundamental. Para ello, podemos hacer una lista por comprensión con la función create_deuteron_hamiltonian que definimos anteriormente.

[4]:

deuteron_hamiltonians = [create_deuteron_hamiltonian(i) for i in range(1, 5)]

En la referencia [1], podemos encontrar las expresiones exactas para el Hamiltoniano del Deuterón de tamaño N = 1, 2 y 3 como se indica a continuación.

\(H_1 = 0.218291(Z_0-I_0)\)

\(H_2 = 5.906709I_1\otimes I_0 + 0.218291I_1\otimes Z_0 - 6.215Z_1\otimes I_0 - 2.143304(X_1\otimes X_0 + Y_1 \otimes Y_0)\)

\(H_3 = I_2\otimes H_2 + 9.625(I_2\otimes I_1\otimes I_0 - Z_2\otimes I_1\otimes I_0) - 3.913119(X_2\otimes X_1\otimes I_0 + Y_2\otimes Y_1\otimes I_0)\)

Si queremos saber si nuestro create_deuteron_hamiltonian nos da el resultado correcto, tenemos que comparar con las expresiones presentadas anteriormente. Para este propósito, imprimimos los Hamiltonianos generados por la función create_deuteron_hamiltonian en la celda de abajo.

[5]:

for i, hamiltonian in enumerate(deuteron_hamiltonians):
    print("Deuteron Hamiltonian: H_{}".format(i + 1))
    print(hamiltonian)
    print("\n")

Deuteron Hamiltonian: H_1
SparsePauliOp(['I', 'Z'],
              coeffs=[-0.21829055+0.j,  0.21829055+0.j])


Deuteron Hamiltonian: H_2
SparsePauliOp(['II', 'IZ', 'XX', 'YY', 'ZI'],
              coeffs=[ 5.90670945+0.j,  0.21829055+0.j, -2.14330352+0.j, -2.14330352+0.j,
 -6.125     +0.j])


Deuteron Hamiltonian: H_3
SparsePauliOp(['III', 'IIZ', 'IXX', 'IYY', 'IZI', 'XXI', 'YYI', 'ZII'],
              coeffs=[15.53170945+0.j,  0.21829055+0.j, -2.14330352+0.j, -2.14330352+0.j,
 -6.125     +0.j, -3.91311896+0.j, -3.91311896+0.j, -9.625     +0.j])


Deuteron Hamiltonian: H_4
SparsePauliOp(['IIII', 'IIIZ', 'IIXX', 'IIYY', 'IIZI', 'IXXI', 'IYYI', 'IZII', 'XXII', 'YYII', 'ZIII'],
              coeffs=[ 28.65670945+0.j,   0.21829055+0.j,  -2.14330352+0.j,  -2.14330352+0.j,
  -6.125     +0.j,  -3.91311896+0.j,  -3.91311896+0.j,  -9.625     +0.j,
  -5.67064811+0.j,  -5.67064811+0.j, -13.125     +0.j])

Al inspeccionar, podemos ver que nuestra función nos está dando el resultado correcto para \(H_1\), \(H_2\) y \(H_3\). Sin embargo, no tenemos una expresión para \(H_4\) en [1], pero es posible decir, por inducción, que el resultado debe ser correcto una vez que los resultados anteriores coincidan con las expresiones dadas en [1].

En [1], los autores trabajaron con ansatze de baja profundidad, porque querían calcular cosas en un dispositivo cuántico real. Esos circuitos cuánticos se pueden encontrar en [1]. Como ya comentamos al comienzo de este tutorial, el hardware cuántico actualmente disponible tiene que trabajar con circuitos cuánticos de baja profundidad para lograr buenos resultados, mientras que aún tengan una cantidad significativa de ruido y no tengan implementada la corrección de errores cuánticos.

Necesitamos definir dos parámetros para construir los circuitos presentados en [1], \(\theta\) (theta) y \(\eta\) (eta), que podemos lograr usando Parameter() como se muestra en el código de la celda a continuación.

[6]:

theta = Parameter(r"$\theta$")
eta = Parameter(r"$\eta$")

Usando los parámetros definidos anteriormente y siguiendo las instrucciones para construir los circuitos presentados en [1], obtenemos los siguientes circuitos:

[7]:

wavefunction = QuantumCircuit(1)
wavefunction.ry(theta, 0)
wavefunction.draw("mpl")

[7]:

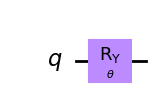
../_images/tutorials_12_deuteron_binding_energy_21_0.png

[8]:

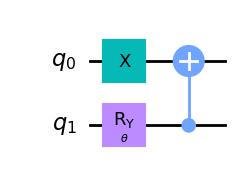
wavefunction2 = QuantumCircuit(2)
wavefunction2.x(0)
wavefunction2.ry(theta, 1)
wavefunction2.cx(1, 0)
wavefunction2.draw("mpl")

[8]:

../_images/tutorials_12_deuteron_binding_energy_22_0.png

[9]:

wavefunction3 = QuantumCircuit(3)
wavefunction3.x(0)
wavefunction3.ry(eta, 1)
wavefunction3.ry(theta, 2)
wavefunction3.cx(2, 0)
wavefunction3.cx(0, 1)
wavefunction3.ry(-eta, 1)
wavefunction3.cx(0, 1)
wavefunction3.cx(1, 0)
wavefunction3.draw("mpl")

[9]:

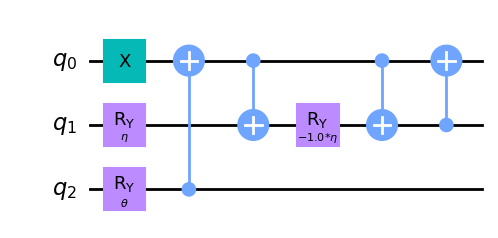
../_images/tutorials_12_deuteron_binding_energy_23_0.png

Desafortunadamente, en [1] no podemos encontrar un circuito de poca profundidad para el ansatz para \(H_4\). Entonces, por ahora no vamos a trabajar con \(N = 4\), pero luego volveremos a este problema usando TwoLocal como ansatz.

Ahora, podemos almacenar estos circuitos en la lista de ansatz para la organización de las pruebas.

[10]:

ansatz = [wavefunction, wavefunction2, wavefunction3]

El tamaño bastante pequeño de nuestros operadores generados nos permite usar funciones de numpy (métodos clásicos) para obtener la energía de enlace para \(H_1\), \(H_2\), \(H_3\) y \(H_4\) a través del proceso de encontrar el valor propio más bajo de las matrices Hamiltonianas. Esta tarea se realiza en el bucle for de la celda de código siguiente.

[11]:

reference_values = []
print("Exact binding energies calculated through numpy.linalg.eigh \n")
for i, hamiltonian in enumerate(deuteron_hamiltonians):
    eigenvalues, eigenstates = np.linalg.eigh(hamiltonian.to_matrix())
    reference_values.append(eigenvalues[0])
    print("Exact binding energy for H_{}: {}".format(i + 1, eigenvalues[0]))

Exact binding energies calculated through numpy.linalg.eigh

Exact binding energy for H_1: -0.43658110999999966
Exact binding energy for H_2: -1.7491598763215301
Exact binding energy for H_3: -2.045670898406441
Exact binding energy for H_4: -2.143981030799862

Los resultados obtenidos anteriormente se utilizarán como nuestros valores de referencia. Así, podemos usarlos para ver si el Estimator nos da buenos resultados. En la siguiente celda de código, ejecutamos el algoritmo VQE para cada par de ansatz y Hamiltoniano, usando el Estimator y el optimizador SLSQP.

[12]:

print(
    "Results using Estimator for H_1, H_2 and H_3 with the ansatz given in the reference paper \n"
)
for i in range(3):
    seed = 42
    algorithm_globals.random_seed = seed
    vqe = VQE(Estimator(), ansatz=ansatz[i], optimizer=SLSQP())
    vqe_result = vqe.compute_minimum_eigenvalue(deuteron_hamiltonians[i])
    binding_energy = vqe_result.optimal_value
    print("Binding energy for H_{}: {} MeV".format(i + 1, binding_energy))

Results using Estimator for H_1, H_2 and H_3 with the ansatz given in the reference paper

Binding energy for H_1: -0.4365811096105766 MeV
Binding energy for H_2: -1.7491595316575452 MeV
Binding energy for H_3: -2.045670898257444 MeV

Podemos ver que nuestros resultados están de acuerdo con los valores de referencia obtenidos por métodos clásicos. También probamos algunas opciones diferentes de optimizadores provistos en Qiskit, porque queríamos saber cuál se comporta mejor. Para ello, hacemos uso de la opción callback en VQE que nos permite almacenar la lista de conteos y valores. Con esta información es posible hacer una gráfica para ver si el optimizador converge al valor de referencia y, si converge, qué tan rápido lo hace. Sin embargo, en la celda de código a continuación, estamos trabajando solo con el optimizador COBYLA en aras de la simplicidad.

[13]:

def callback(eval_count, parameters, mean, std):
    # Overwrites the same line when printing
    display("Evaluation: {}, Energy: {}, Std: {}".format(eval_count, mean, std))
    clear_output(wait=True)
    counts.append(eval_count)
    values.append(mean)
    params.append(parameters)
    deviation.append(std)

[14]:

plots = []

for i in range(3):

    counts = []
    values = []
    params = []
    deviation = []
    seed = 42
    algorithm_globals.random_seed = seed
    vqe = VQE(Estimator(), ansatz=ansatz[i], optimizer=COBYLA(), callback=callback)
    vqe_result = vqe.compute_minimum_eigenvalue(deuteron_hamiltonians[i])
    plots.append([counts, values])

'Evaluation: 45, Energy: -2.045670636012936, Std: {}'

Graficar los resultados obtenidos con la ejecución de VQE sobre la celda de código anterior.

[15]:

fig, ax = plt.subplots(nrows=3, ncols=1)
fig.set_size_inches((12, 12))
for i, plot in enumerate(plots):
    ax[i].plot(plot[0], plot[1], "o-", label="COBYLA")
    ax[i].axhline(
        y=reference_values[i],
        color="k",
        linestyle="--",
        label=f"Reference Value: {reference_values[i]}",
    )
    ax[i].legend()
    ax[i].set_xlabel("Cost Function Evaluations", fontsize=15)
    ax[i].set_ylabel(r"$\langle H_{} \rangle$ - Energy (MeV)".format(i + 1), fontsize=15)
plt.show()

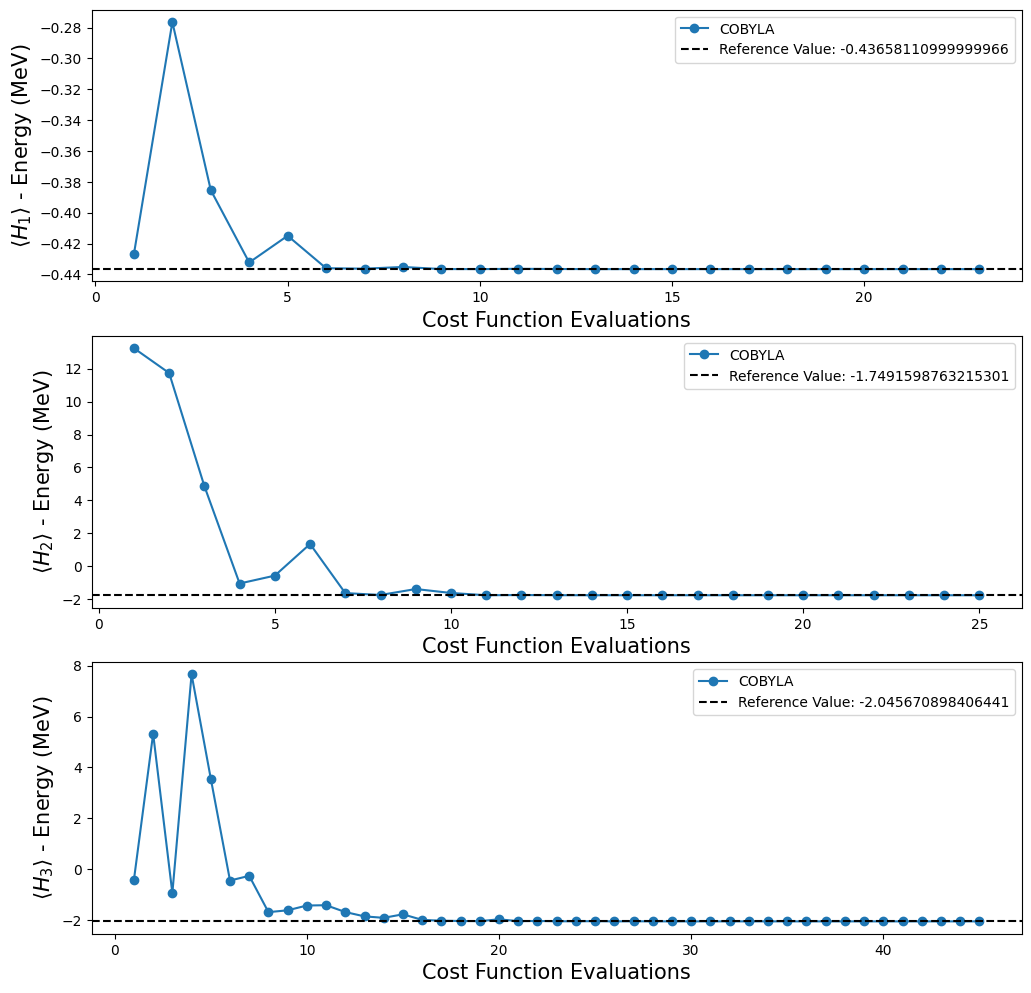
../_images/tutorials_12_deuteron_binding_energy_35_0.png

Ten en cuenta que con los circuitos cuánticos dados en [1], no podemos probar si podemos alcanzar el valor de referencia para \(H_4\), porque, como se mencionó antes, no tenemos un ansatz para este Hamiltoniano. Afortunadamente, ese no es el final de nuestros experimentos, porque Qiskit proporciona algunas funciones que crean un ansatz para nosotros. Para nuestros propósitos, decidimos usar la función TwoLocal para construir nuestro nuevo ansatz. En la siguiente celda de código, usamos un bucle for para crear una lista con el ansatz TwoLocal para cada Hamiltoniano.

[16]:

twolocal_ansatzes = []
for i in range(1, 5):
    ansatz = TwoLocal(
        deuteron_hamiltonians[i - 1].num_qubits,
        ["rz", "ry"],
        "cx",
        entanglement="full",
        reps=i,
        initial_state=None,
    )
    twolocal_ansatzes.append(ansatz)

Ahora podemos comprobar si con este nuevo tipo de ansatz podemos alcanzar los valores de referencia obtenidos por métodos clásicos. Para hacer esta verificación, tenemos que repetir los experimentos hechos anteriormente, pero ahora usando el ansatz definido mediante el uso de la función TwoLocal.

[17]:

print("Results using Estimator for H_1, H_2, H_3 and H_4 with TwoLocal ansatz \n")
seed = 42
algorithm_globals.random_seed = seed
for i in range(4):
    vqe = VQE(Estimator(), ansatz=twolocal_ansatzes[i], optimizer=SLSQP())
    vqe_result = vqe.compute_minimum_eigenvalue(deuteron_hamiltonians[i])
    binding_energy = vqe_result.optimal_value
    print("Binding energy for H_{}:".format(i + 1), binding_energy, "MeV")

Results using Estimator for H_1, H_2, H_3 and H_4 with TwoLocal ansatz

Binding energy for H_1: -0.4365806560191138 MeV
Binding energy for H_2: -1.7491598681936242 MeV
Binding energy for H_3: -2.045670763548605 MeV
Binding energy for H_4: -2.1439130048015045 MeV

[18]:

seed = 42
algorithm_globals.random_seed = seed

plots_tl = []
for i in range(4):

    counts = []
    values = []
    params = []
    deviation = []
    vqe = VQE(
        Estimator(),
        ansatz=twolocal_ansatzes[i],
        optimizer=SLSQP(),
        callback=callback,
    )
    vqe_result = vqe.compute_minimum_eigenvalue(deuteron_hamiltonians[i])
    plots_tl.append([counts, values])

'Evaluation: 4149, Energy: -2.143913004801629, Std: {}'

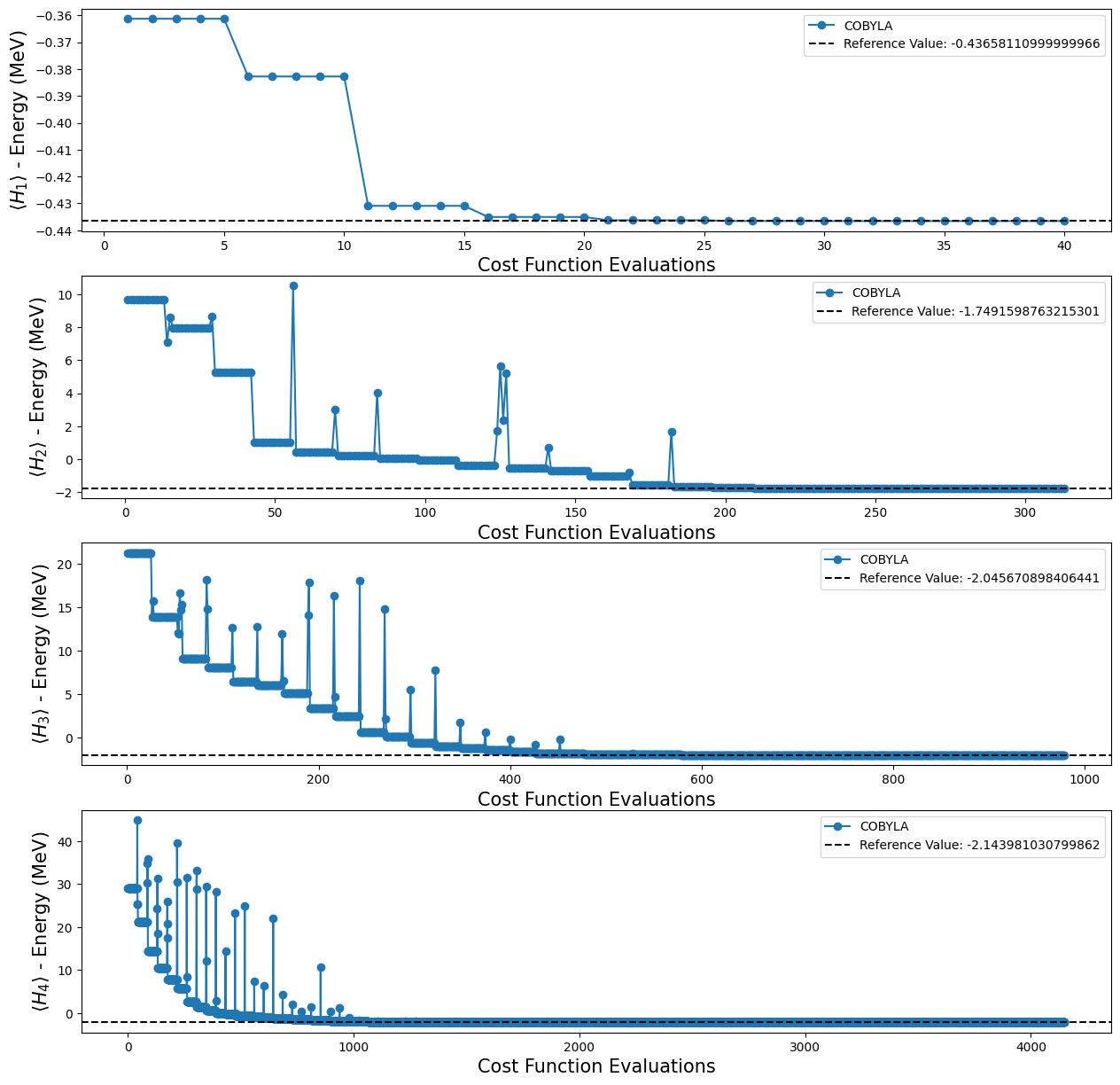
Usando los cuatro ansatze TwoLocal diferentes, obtuvimos los siguientes resultados:

[19]:

fig, ax = plt.subplots(nrows=4, ncols=1)
fig.set_size_inches((15, 15))
for i, plot in enumerate(plots_tl):
    ax[i].plot(plot[0], plot[1], "o-", label="COBYLA")
    ax[i].axhline(
        y=reference_values[i],
        color="k",
        linestyle="--",
        label=f"Reference Value: {reference_values[i]}",
    )
    ax[i].legend()
    ax[i].set_xlabel("Cost Function Evaluations", fontsize=15)
    ax[i].set_ylabel(r"$\langle H_{} \rangle$ - Energy (MeV)".format(i + 1), fontsize=15)
plt.show()

../_images/tutorials_12_deuteron_binding_energy_42_0.png

Paso 4: Calcular los valores esperados de los observables#

Uno de nuestros objetivos en el proyecto Qiskit Advocate Mentorship Program era mostrar que es posible calcular los valores esperados de algunos observables de interés y mostrar cómo se comportan cuando variamos un parámetro en el circuito ansatz. En nuestro caso, los observables de interés fueron \(I_1 \otimes Z_0\), \(Z_1 \otimes I_0\), \(X_1 \otimes X_0\), \(Y_1 \otimes Y_0\) y \(H_2\), luego investigamos su comportamiento cuando el parámetro \(\theta\) fue variado dentro del intervalo \([-\pi,\pi]\).

En la notación de Dirac (bra-ket), la definición del valor esperado de un observable \(\hat{O}\) es igual a [3] [4]:

\(\langle \hat{O} \rangle_\psi = \langle \psi(\vec{\theta})|\hat{O}|\psi(\vec{\theta}) \rangle\).

El siguiente código define una función que calcula los valores esperados de los observables, dado un circuito cuántico parametrizado y una lista con algunos valores para estos parámetros (ángulos).

[20]:

def calculate_observables_exp_values(
    quantum_circuit: QuantumCircuit, observables: list, angles: list
) -> list:
    """Calculate the expectation value of an observable given the quantum
    circuit that represents the wavefunction and a list of parameters.

        Args:
            quantum_circuit (QuantumCircuit): A parameterized quantum circuit
            that represents the wavefunction of the system.

            observables (list): A list containing the observables that we want
            to know the expectation values.

            angles (list): A list with the values that will be used in the
            'bind_parameters' method.

        Returns:
            list_exp_values (list): A list containing the expectation values
            of the observables given as input.
    """
    list_exp_values = []
    for observable in observables:
        exp_values = []
        for angle in angles:
            qc = quantum_circuit.bind_parameters({theta: angle})
            result = estimate_observables(
                Estimator(),
                quantum_state=qc,
                observables=[observable],
            )

            exp_values.append(result[0][0])
        list_exp_values.append(exp_values)

    return list_exp_values

Cálculo del valor esperado de los observables de interés utilizando la función definida anteriormente:

[21]:

angles = list(np.linspace(-np.pi, np.pi, 100))
observables = [
    Pauli("IZ"),
    Pauli("ZI"),
    Pauli("XX"),
    Pauli("YY"),
    deuteron_hamiltonians[1],
]
h2_observables_exp_values = calculate_observables_exp_values(wavefunction2, observables, angles)

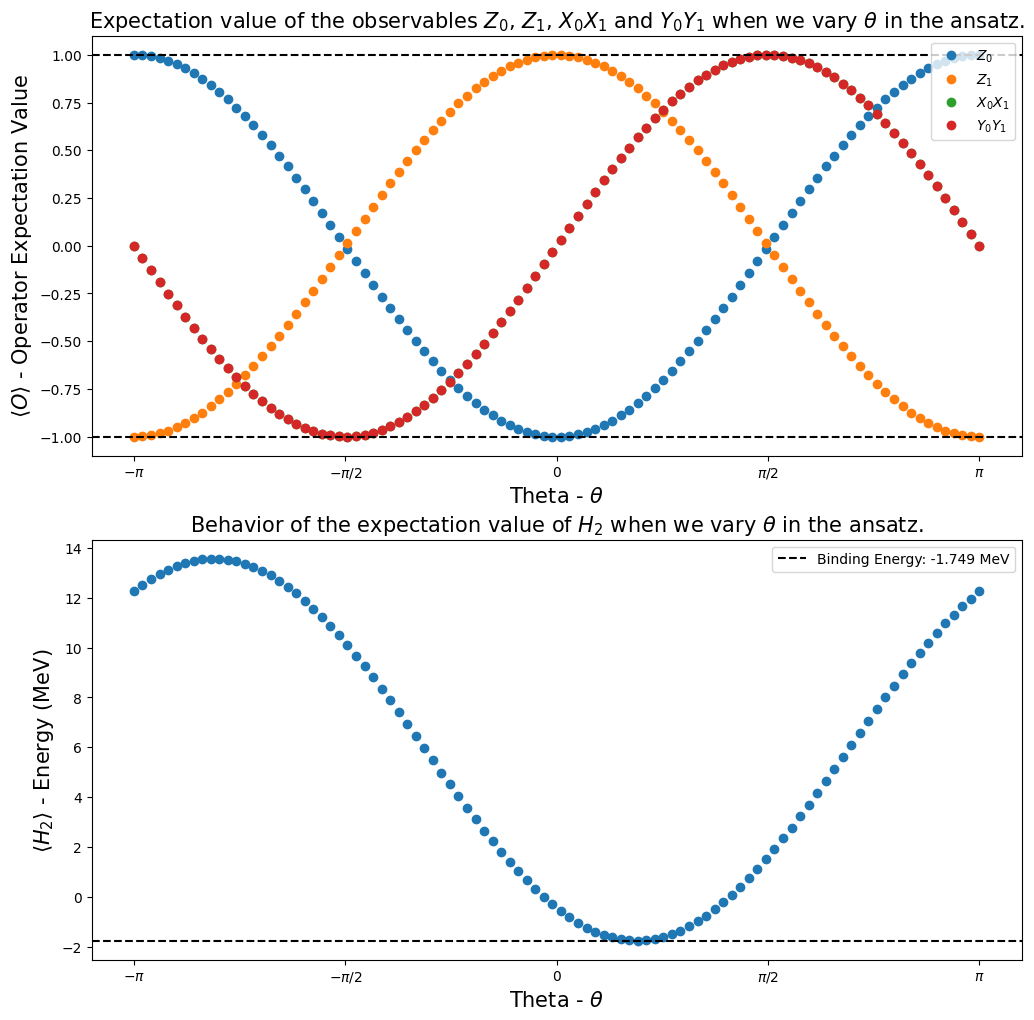
Usando la función calculate_observables_exp_values (la definimos en el Paso 2), obtuvimos las gráficas que se presentan a continuación. Nos mostraron que podíamos reproducir los resultados de [1].

[22]:

fig, ax = plt.subplots(nrows=2, ncols=1)
fig.set_size_inches((12, 12))
ax[0].plot(angles, h2_observables_exp_values[0], "o", label=r"$Z_0$")
ax[0].plot(angles, h2_observables_exp_values[1], "o", label=r"$Z_1$")
ax[0].plot(angles, h2_observables_exp_values[2], "o", label=r"$X_0X_1$")
ax[0].plot(angles, h2_observables_exp_values[3], "o", label=r"$Y_0Y_1$")
ax[0].axhline(
    y=1,
    color="k",
    linestyle="--",
)
ax[0].axhline(y=-1, color="k", linestyle="--")
ax[0].legend()
ax[0].set_xlabel(r"Theta - $\theta$", fontsize=15)
ax[0].set_ylabel(r"$\langle O \rangle $ - Operator Expectation Value", fontsize=15)
ax[0].set_xticks(
    [-np.pi, -np.pi / 2, 0, np.pi / 2, np.pi],
    labels=[r"$-\pi$", r"$-\pi/2$", "0", r"$\pi/2$", r"$\pi$"],
)
ax[0].set_title(
    r"Expectation value of the observables $Z_0$, $Z_1$, $X_0X_1$ and $Y_0Y_1$ when we vary $\theta$ in the ansatz.",
    fontsize=15,
)
ax[1].plot(angles, h2_observables_exp_values[4], "o")
ax[1].axhline(
    y=reference_values[1],
    color="k",
    linestyle="--",
    label="Binding Energy: {} MeV".format(np.round(reference_values[1], 3)),
)
ax[1].legend()
ax[1].set_xlabel(r"Theta - $\theta$", fontsize=15)
ax[1].set_ylabel(r"$\langle H_2 \rangle $ - Energy (MeV)", fontsize=15)
ax[1].set_xticks(
    [-np.pi, -np.pi / 2, 0, np.pi / 2, np.pi],
    labels=[r"$-\pi$", r"$-\pi/2$", "0", r"$\pi/2$", r"$\pi$"],
)
ax[1].set_title(
    r"Behavior of the expectation value of $H_2$ when we vary $\theta$ in the ansatz.", fontsize=15
)

plt.show()

../_images/tutorials_12_deuteron_binding_energy_50_0.png

Reconocimiento#

Me gustaría agradecer a Steve Wood, Soham Pal y Siddhartha Morales por los debates en nuestras reuniones durante el Qiskit Advocate Mentorship Program 2021 - Fall, fueron muy importantes para la construcción de este tutorial.

Referencias#

[1] Dumitrescu, Eugene F., et al. «Cloud quantum computing of an atomic nucleus.» Physical review letters 120.21 (2018): 210501. Arxiv version: https://arxiv.org/pdf/1801.03897.pdf

[2] Qiskit Nature Documentation. https://qiskit.org/documentation/nature/

[3] Feynman, R. P., Robert B. Leighton, and Matthew Sands. «The Feynman Lectures on Physics, Volume III: Quantum Mechanics, vol. 3.» (2010). https://www.feynmanlectures.caltech.edu/III_toc.html

[4] Expectation value (quantum mechanics) Wikipedia article. https://en.wikipedia.org/wiki/Expectation_value_(quantum_mechanics)

[23]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
`qiskit-terra`	0.24.0.dev0+2b3686f
`qiskit-aer`	0.11.2
`qiskit-ibmq-provider`	0.19.2
`qiskit-nature`	0.6.0
System information
Python version	3.9.16
Python compiler	GCC 12.2.1 20221121 (Red Hat 12.2.1-4)
Python build	main, Dec 7 2022 00:00:00
OS	Linux
CPUs	8
Memory (Gb)	62.50002670288086
Thu Apr 06 09:19:48 2023 CEST

This code is a part of Qiskit

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.