Nota
Esta página fue generada a partir de docs/tutorials/03_ground_state_solvers.ipynb.
Solucionadores de estado fundamental#
Introducción#
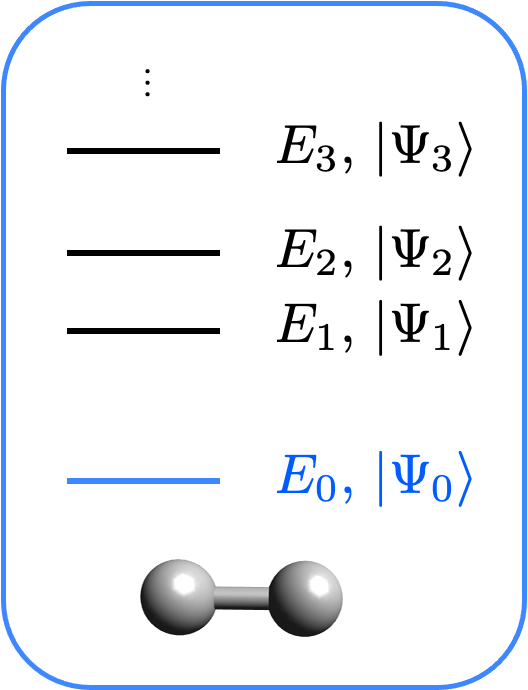
En este tutorial vamos a discutir la interfaz del cálculo del estado fundamental de Qiskit Nature. El objetivo es calcular el estado fundamental de un Hamiltoniano molecular. Este Hamiltoniano puede ser electrónico o vibracional. Para saber más sobre la preparación del Hamiltoniano, consulta los tutoriales de Estructura electrónica y Estructura vibracional.
Debe decirse que, en el caso electrónico, en realidad estamos calculando puramente la parte electrónica. Al usar la pila de Qiskit Nature como se presenta en este tutorial, la energía de repulsión nuclear se agregará automáticamente para obtener la energía del estado fundamental total.
El primer paso es definir el sistema molecular. A continuación, pedimos la parte electrónica de una molécula de hidrógeno.
[1]:
from qiskit_nature.units import DistanceUnit
from qiskit_nature.second_q.drivers import PySCFDriver
driver = PySCFDriver(
atom="H 0 0 0; H 0 0 0.735",
basis="sto3g",
charge=0,
spin=0,
unit=DistanceUnit.ANGSTROM,
)
es_problem = driver.run()
También nos apegaremos al mapeo de Jordan-Wigner. Para obtener más información sobre los diversos mapeadores disponibles en Qiskit Nature, consulta el Tutorial de Mapeadores de Qubit.
[2]:
from qiskit_nature.second_q.mappers import JordanWignerMapper
mapper = JordanWignerMapper()
El Solucionador#
Después de estos pasos, necesitamos definir un solucionador. El solucionador es el algoritmo a través del cual se calcula el estado fundamental.
Comencemos primero con un ejemplo puramente clásico: el NumPyMinimumEigensolver. Este algoritmo diagonaliza exactamente al Hamiltoniano. Aunque escala mal, se puede usar en sistemas pequeños para verificar los resultados de los algoritmos cuánticos.
[3]:
from qiskit_algorithms import NumPyMinimumEigensolver
numpy_solver = NumPyMinimumEigensolver()
Para encontrar el estado fundamental también podríamos usar el algoritmo de Solucionador Propio Cuántico Variacional (Variational Quantum Eigensolver, VQE). El algoritmo VQE funciona intercambiando información entre una computadora clásica y una computadora cuántica, cómo se muestra en la siguiente figura.
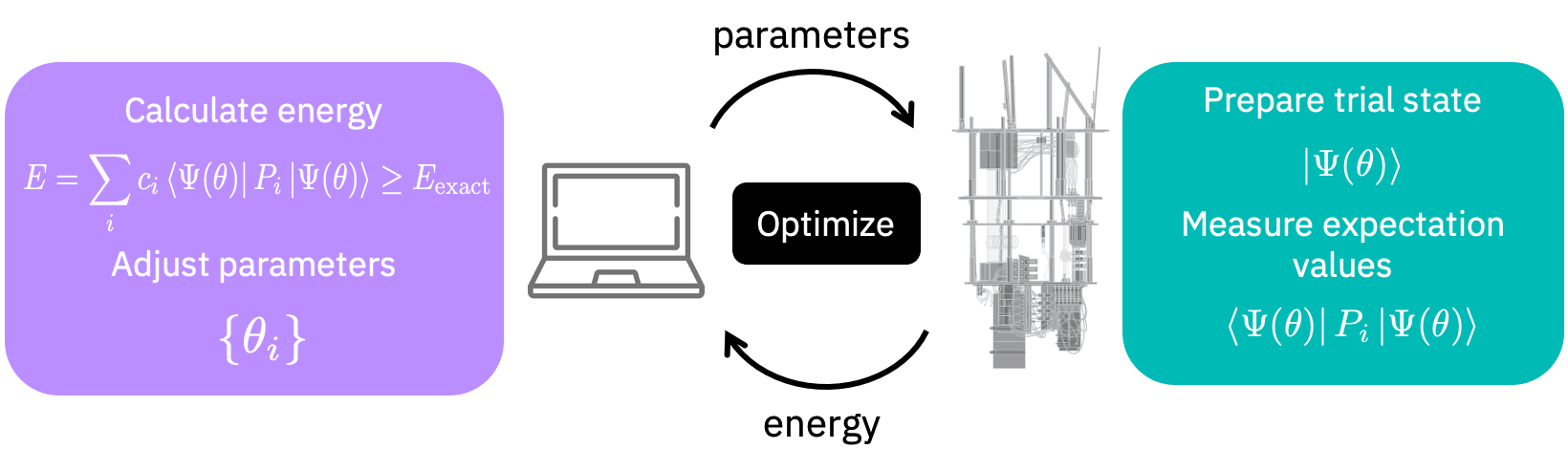
Inicialicemos un solucionador de VQE.
[4]:
from qiskit_algorithms import VQE
from qiskit_algorithms.optimizers import SLSQP
from qiskit.primitives import Estimator
from qiskit_nature.second_q.circuit.library import HartreeFock, UCCSD
ansatz = UCCSD(
es_problem.num_spatial_orbitals,
es_problem.num_particles,
mapper,
initial_state=HartreeFock(
es_problem.num_spatial_orbitals,
es_problem.num_particles,
mapper,
),
)
vqe_solver = VQE(Estimator(), ansatz, SLSQP())
vqe_solver.initial_point = [0.0] * ansatz.num_parameters
Para definir el solucionador de VQE necesitamos tres elementos esenciales:
Una primitiva de Estimator: estas se lanzaron como parte de Qiskit Terra 0.22. Para obtener más información sobre las primitivas, consulta este recurso.
Una forma variacional: aquí usamos el ansatz Clúster Acoplado Unitario (Unitary Coupled Cluster, UCC) (ver por ejemplo [Physical Review A 98.2 (2018): 022322]). Dado que es un estándar de química, ya está disponible una fábrica que permite una inicialización rápida de un VQE con UCC. El valor predeterminado es usar todas las excitaciones simples y dobles. Sin embargo, se puede seleccionar el tipo de excitación (S, D, SD) así como otros parámetros. También anteponemos la forma variacional
UCCSDcon un estado inicialHartreeFock, que inicializa la ocupación de nuestros qubits de acuerdo con el problema que estamos tratando de resolver.Un optimizador: este es el clásico fragmento de código encargado de optimizar los parámetros en nuestra forma variacional. Consulta la documentación correspondiente para obtener más información.
Uno podría usar cualquier ansatz / estado inicial disponible, o incluso definir uno propio. Por ejemplo,
[5]:
from qiskit_algorithms import VQE
from qiskit.circuit.library import TwoLocal
tl_circuit = TwoLocal(
rotation_blocks=["h", "rx"],
entanglement_blocks="cz",
entanglement="full",
reps=2,
parameter_prefix="y",
)
another_solver = VQE(Estimator(), tl_circuit, SLSQP())
El cálculo y los resultados#
Ahora estamos listos para juntar todo para calcular el estado fundamental de nuestro problema. Hacerlo requiere que empaquetemos nuestro mapper y el algoritmo cuántico en un solo GroundStateEigensolver de la siguiente manera:
[6]:
from qiskit_nature.second_q.algorithms import GroundStateEigensolver
calc = GroundStateEigensolver(mapper, vqe_solver)
Esto ahora tomará todo el flujo de trabajo: 1. generar los operadores de segunda cuantización almacenados en nuestro problema (aquí referido como es_problem) 2. mapear (y potencialmente reducir) los operadores en el espacio de qubits 3. ejecutar el algoritmo cuántico en el Hamiltoniano del operador de qubit 4. una vez convergido, evaluar los observables adicionales en el estado fundamental determinado
[7]:
res = calc.solve(es_problem)
print(res)
=== GROUND STATE ENERGY ===
* Electronic ground state energy (Hartree): -1.857275030145
- computed part: -1.857275030145
~ Nuclear repulsion energy (Hartree): 0.719968994449
> Total ground state energy (Hartree): -1.137306035696
=== MEASURED OBSERVABLES ===
0: # Particles: 2.000 S: 0.000 S^2: 0.000 M: 0.000
=== DIPOLE MOMENTS ===
~ Nuclear dipole moment (a.u.): [0.0 0.0 1.3889487]
0:
* Electronic dipole moment (a.u.): [0.0 0.0 1.38894893]
- computed part: [0.0 0.0 1.38894893]
> Dipole moment (a.u.): [0.0 0.0 -0.00000023] Total: 0.00000023
(debye): [0.0 0.0 -0.00000058] Total: 0.00000058
Podemos comparar los resultados de VQE con el solucionador exacto de NumPy y ver que sí coinciden.
[8]:
calc = GroundStateEigensolver(mapper, numpy_solver)
res = calc.solve(es_problem)
print(res)
=== GROUND STATE ENERGY ===
* Electronic ground state energy (Hartree): -1.857275030202
- computed part: -1.857275030202
~ Nuclear repulsion energy (Hartree): 0.719968994449
> Total ground state energy (Hartree): -1.137306035753
=== MEASURED OBSERVABLES ===
0: # Particles: 2.000 S: 0.000 S^2: 0.000 M: 0.000
=== DIPOLE MOMENTS ===
~ Nuclear dipole moment (a.u.): [0.0 0.0 1.3889487]
0:
* Electronic dipole moment (a.u.): [0.0 0.0 1.3889487]
- computed part: [0.0 0.0 1.3889487]
> Dipole moment (a.u.): [0.0 0.0 0.0] Total: 0.0
(debye): [0.0 0.0 0.0] Total: 0.0
Usar una función de filtro#
A veces el verdadero estado fundamental del Hamiltoniano no es de interés, ya que yace en un sector de simetría distinto del espacio de Hilbert. En este caso, el NumPyEigensolver puede tomar una función filtro para devolver solo los estados propios con, por ejemplo, el número correcto de partículas. Esto es de particular importancia en el caso de los cálculos de estructuras vibracionales donde el verdadero estado fundamental del Hamiltoniano es el estado de vacío cuántico. Una función de filtro predeterminada para revisar el número de partículas es implementada en los diferentes problemas y puede ser usada como sigue:
[9]:
from qiskit_algorithms import NumPyMinimumEigensolver
from qiskit_nature.second_q.drivers import GaussianForcesDriver
from qiskit_nature.second_q.mappers import DirectMapper
from qiskit_nature.second_q.problems import HarmonicBasis
driver = GaussianForcesDriver(logfile="aux_files/CO2_freq_B3LYP_631g.log")
basis = HarmonicBasis([2, 2, 2, 2])
vib_problem = driver.run(basis=basis)
vib_problem.hamiltonian.truncation_order = 2
mapper = DirectMapper()
solver_without_filter = NumPyMinimumEigensolver()
solver_with_filter = NumPyMinimumEigensolver(
filter_criterion=vib_problem.get_default_filter_criterion()
)
gsc_wo = GroundStateEigensolver(mapper, solver_without_filter)
result_wo = gsc_wo.solve(vib_problem)
gsc_w = GroundStateEigensolver(mapper, solver_with_filter)
result_w = gsc_w.solve(vib_problem)
print(result_wo)
print("\n\n")
print(result_w)
=== GROUND STATE ===
* Vibrational ground state energy (cm^-1): -8e-12
The number of occupied modals for each mode is:
- Mode 0: 0.0
- Mode 1: 0.0
- Mode 2: 0.0
- Mode 3: 0.0
=== GROUND STATE ===
* Vibrational ground state energy (cm^-1): 2432.106954036546
The number of occupied modals for each mode is:
- Mode 0: 1.0
- Mode 1: 1.0
- Mode 2: 1.0
- Mode 3: 1.0
[10]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.24.0.dev0+2b3686f |
qiskit-aer | 0.11.2 |
qiskit-ibmq-provider | 0.19.2 |
qiskit-nature | 0.6.0 |
| System information | |
| Python version | 3.9.16 |
| Python compiler | GCC 12.2.1 20221121 (Red Hat 12.2.1-4) |
| Python build | main, Dec 7 2022 00:00:00 |
| OS | Linux |
| CPUs | 8 |
| Memory (Gb) | 62.50002670288086 |
| Thu Apr 06 08:55:38 2023 CEST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.