Randomized measurements¶
This tutorial shows the different randomized measurements of the povm_toolbox.
[1]:
%load_ext autoreload
%autoreload 2
Circuit and Observables¶
We first look at a random the 2-qubit circuit, with depth 3.
[2]:
from qiskit.circuit import ClassicalRegister, QuantumCircuit
from qiskit.circuit.library import XXMinusYYGate
num_qubits = 2
# circuit originally generated by
# `random_circuit(num_qubits=num_qubits, depth=3, measure=False, seed=0)`
qc_random = QuantumCircuit(2)
qc_random.append(XXMinusYYGate(1.7, 0.257), [0, 1])
qc_random.rx(5.74, qubit=0)
qc_random.id(qubit=1)
qc_random.ch(control_qubit=1, target_qubit=0)
creg = ClassicalRegister(1)
qc_random.add_register(creg)
qc_random.draw("mpl", style="iqp")
[2]:
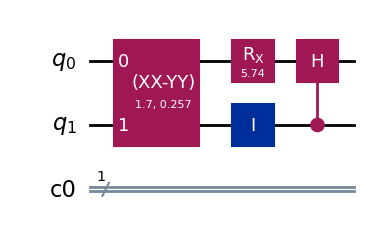
We also draw 3 random observables.
[3]:
from qiskit.quantum_info import SparsePauliOp
set_observables = [
SparsePauliOp(["II", "XX", "YY", "ZY"], coeffs=[1, 1, -4, 1]),
SparsePauliOp(["XI", "ZX", "YI"], coeffs=[1, -1, 2.5]),
SparsePauliOp(["II", "XI", "ZI", "IX", "IY", "YX"], coeffs=[0.4, 4, -1, 1, -0.5, 1.8]),
]
For reference, we compute the true final state and the exact expectation values for the different observables.
[4]:
import numpy as np
from qiskit.quantum_info import Statevector
exact_state = Statevector(qc_random)
exp_val = np.real_if_close(
np.array([exact_state.expectation_value(obs) for obs in set_observables])
)
Classical Shadows¶
We now look at the implementation of Classical Shadows measurement.
[5]:
from povm_toolbox.library import ClassicalShadows
# By default, the Classical Shadows (CS) measurement uses Z-,X-,Y-measurements with equal probability.
cs_implementation = ClassicalShadows(num_qubits=num_qubits, seed=23)
# Define the default shot budget.
cs_shots = 4096
# Construct the `POVMSamplerPub`.
cs_pub = (qc_random, None, cs_shots, cs_implementation)
Locally-Biased Classical Shadows¶
We now look at Classical Shadows that can be locally-biased.
[6]:
from povm_toolbox.library import LocallyBiasedClassicalShadows
# Set the distributions of the shots among the Z-,X-,Y-measurements (in this order).
bias = np.array(
[
[
0.0000000028, # bias for Z-measurements on first qubit
0.4408677642, # bias for X-measurements on first qubit
0.5591322330, # bias for Y-measurements on first qubit
],
[
0.1989721524, # bias for Z-measurements on second qubit
0.3190601952, # bias for X-measurements on second qubit
0.4819676524, # bias for Y-measurements on second qubit
],
]
)
# The Locally-Biased Classical Shadows (LBCS) measurement uses Z-,X-,Y-measurements with different probabilities.
lbcs_implementation = LocallyBiasedClassicalShadows(num_qubits=num_qubits, bias=bias, seed=24)
# Define the default shot budget.
lbcs_shots = 4096
# Construct the `POVMSamplerPub`.
lbcs_pub = (qc_random, None, lbcs_shots, lbcs_implementation)
Mutually-Unbiased-Bases POVM¶
We now look at POVMs that are rotated locally-biased Classical Shadows.
[7]:
from povm_toolbox.library import MutuallyUnbiasedBasesMeasurements
# Define the Euler angles to rotate the measurement.
angles = np.array(
[
[0.0000027222, 0.0000000910, 0.3],
[0.0000022917, 0.0000002655, 0.0],
]
)
# Set the distributions of the shots among the PMs.
bias = np.array(
[
[0.0000372719, 0.4377084332, 0.5622542949],
[0.2002136793, 0.3192036469, 0.4805826738],
]
)
# Define the PM-simulable POVM.
mub_implementation = MutuallyUnbiasedBasesMeasurements(
num_qubits=num_qubits, bias=bias, angles=angles, seed=12
)
# Define the default shot budget.
mub_shots = 4100
# Construct the `POVMSamplerPub`.
mub_pub = (qc_random, None, mub_shots, mub_implementation)
PM-simulable POVM¶
We now look at POVMs that are simulable (through randomization) with only single-qubit projective measurements (PMs).
[8]:
from povm_toolbox.library import RandomizedProjectiveMeasurements
# Define our projective measurements acting on each qubit.
angles = np.array(
[
[0.0000027222, 0.0000000910, 1.5707688831, 0.0000235665, 1.5707519773, 1.5707694998],
[0.0000022917, 0.0000002655, 1.5707961328, 0.0000069500, 1.5707958682, 1.5708006931],
]
)
# Set the distributions of the shots among the PMs.
bias = np.array(
[
[0.0000372719, 0.4377084332, 0.5622542949],
[0.2002136793, 0.3192036469, 0.4805826738],
]
)
# Define the PM-simulable POVM.
pmsim_implementation = RandomizedProjectiveMeasurements(
num_qubits=num_qubits, bias=bias, angles=angles, seed=25
)
# Define the default shot budget.
pmsim_shots = 4100
# Construct the `POVMSamplerPub`.
pmsim_pub = (qc_random, None, pmsim_shots, pmsim_implementation)
POVM Sampler¶
We now instantiate the POVMSampler that will use the different POVM measurements.
[9]:
from numpy.random import default_rng
from povm_toolbox.sampler.povm_sampler import POVMSampler
from qiskit.primitives import StatevectorSampler
# First define a standard sampler (that will be used under the hood).
sampler = StatevectorSampler(seed=default_rng(0))
# Then define the POVM sampler, which takes BaseSampler as an argument.
povm_sampler = POVMSampler(sampler)
# Submit the job by specifying which POVM to use, which circuit(s) to measure and the shot budget.
job = povm_sampler.run([cs_pub, lbcs_pub, mub_pub, pmsim_pub])
Results¶
We retrieve the result object, which contains the POVM used and from which we can query the counts of each outcome.
[10]:
from povm_toolbox.post_processor.povm_post_processor import POVMPostProcessor
# Retrieve the `PrimitiveResult` object, which contains 3 `POVMPubResult` objects.
result = job.result()
print(f"\n{'-':-<85}-\n")
# Loop through the different PUB results
for k, pub_result in enumerate(result):
# Instantiate the post-processor from the PUB result.
post_processor = POVMPostProcessor(pub_result)
print(f"PUB number : {k}")
# If one wants to explicitly retrieve the POVM used for a specific PUB,
# it can be accessed through the metadata of the PUB result.
print(f"POVM class: {pub_result.metadata.povm_implementation}")
print(f"Number of shots : {sum(post_processor.counts[0].values())}\n")
print(" Exact Estimate Error Estimated std z-score")
for i, obs in enumerate(set_observables):
cs_est_exp_val, std = post_processor.get_expectation_value(obs)
print(
f" {np.real(exp_val[i]):>10.3e} {cs_est_exp_val:>12.3e} {abs(cs_est_exp_val - np.real(exp_val[i])) / abs(np.real(exp_val[i])):>8.1%}",
end=" ",
)
print(f" {std:> 8.5f} {(cs_est_exp_val - np.real(exp_val[i])) / std:> 11.2f}")
print(f"\n{'-':-<85}-\n")
--------------------------------------------------------------------------------------
PUB number : 0
POVM class: ClassicalShadows(num_qubits=2)
Number of shots : 4096
Exact Estimate Error Estimated std z-score
1.470e+00 1.347e+00 8.4% 0.19243 -0.64
-1.420e+00 -1.294e+00 8.8% 0.08414 1.49
2.947e+00 3.072e+00 4.2% 0.12670 0.98
--------------------------------------------------------------------------------------
PUB number : 1
POVM class: LocallyBiasedClassicalShadows(num_qubits=2, bias=array([[2.80000000e-09, 4.40867764e-01, 5.59132233e-01],
[1.98972152e-01, 3.19060195e-01, 4.81967652e-01]]))
Number of shots : 4096
Exact Estimate Error Estimated std z-score
1.470e+00 1.533e+00 4.3% 0.13764 0.46
-1.420e+00 -1.532e+00 7.9% 0.07798 -1.44
2.947e+00 2.920e+00 0.9% 0.11659 -0.24
--------------------------------------------------------------------------------------
PUB number : 2
POVM class: MutuallyUnbiasedBasesMeasurements(num_qubits=2, bias=array([[3.72719000e-05, 4.37708433e-01, 5.62254295e-01],
[2.00213679e-01, 3.19203647e-01, 4.80582674e-01]]), angles=array([[2.7222e-06, 9.1000e-08, 3.0000e-01],
[2.2917e-06, 2.6550e-07, 0.0000e+00]]))
Number of shots : 4100
Exact Estimate Error Estimated std z-score
1.470e+00 1.495e+00 1.7% 0.13698 0.18
-1.420e+00 -1.497e+00 5.5% 0.07997 -0.97
2.947e+00 2.826e+00 4.1% 0.11678 -1.04
--------------------------------------------------------------------------------------
PUB number : 3
POVM class: RandomizedProjectiveMeasurements(num_qubits=2, bias=array([[3.72719000e-05, 4.37708433e-01, 5.62254295e-01],
[2.00213679e-01, 3.19203647e-01, 4.80582674e-01]]), angles=array([[[2.72220000e-06, 9.10000000e-08],
[1.57076888e+00, 2.35665000e-05],
[1.57075198e+00, 1.57076950e+00]],
[[2.29170000e-06, 2.65500000e-07],
[1.57079613e+00, 6.95000000e-06],
[1.57079587e+00, 1.57080069e+00]]]))
Number of shots : 4100
Exact Estimate Error Estimated std z-score
1.470e+00 1.521e+00 3.4% 0.13332 0.38
-1.420e+00 -1.495e+00 5.3% 0.07798 -0.97
2.947e+00 3.054e+00 3.6% 0.11699 0.91
--------------------------------------------------------------------------------------
[11]:
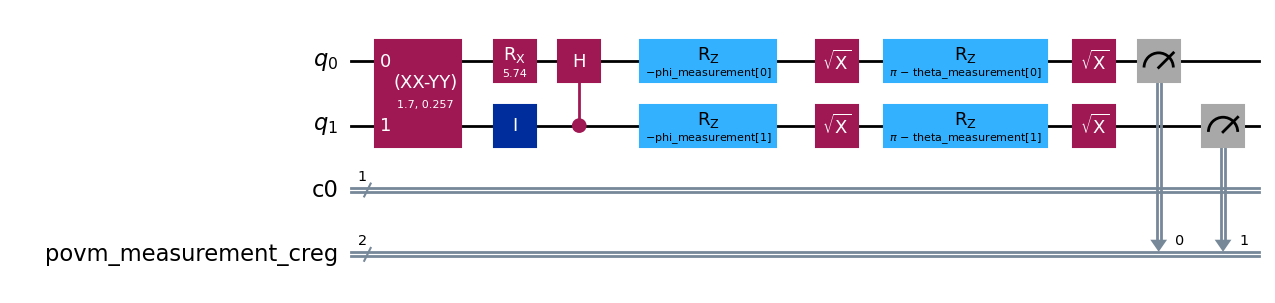
# Inspect one of the circuit sent to the internal `BaseSamplerV2` sampler:
lbcs_composed_circuit = result[1].metadata.composed_circuit
lbcs_composed_circuit.draw("mpl", style="iqp")
[11]: