SingleQubitPOVM

class SingleQubitPOVM(list_operators: list[Operator])

Bases: MultiQubitPOVM

A convenience class to represent a single-qubit MultiQubitPOVM instance.

Below is a simple example showing how you define a symmetric and informationally-complete POVM (SIC-POVM):

>>> import cmath
>>> import numpy as np
>>> from povm_toolbox.quantum_info import SingleQubitPOVM
>>> vecs = np.sqrt(1.0 / 2.0) * np.array(
...     [
...         [1, 0],
...         [np.sqrt(1.0 / 3.0), np.sqrt(2.0 / 3.0)],
...         [np.sqrt(1.0 / 3.0), np.sqrt(2.0 / 3.0) * cmath.exp(2.0j * np.pi / 3)],
...         [np.sqrt(1.0 / 3.0), np.sqrt(2.0 / 3.0) * cmath.exp(4.0j * np.pi / 3)],
...     ]
... )
>>> sic_povm = SingleQubitPOVM.from_vectors(vecs)
>>> print(sic_povm)
SingleQubitPOVM<4> at 0x...

Initialize from explicit operators.

Parameters:

list_operators (list[Operator]) – list that contains the explicit frame operators. The length of the list is the number of operators of the frame.

Raises:

ValueError – if the frame operators do not have a correct shape. They should all be hermitian and of the same dimension.

Inherited Attributes

dimension

The dimension of the Hilbert space on which the effects act.

informationally_complete

If the frame spans the entire Hilbert space.

num_operators

The number of effects of the frame.

num_outcomes

The number of outcomes of the POVM.

num_subsystems

The number of subsystems which the frame operators act on.

For qubits, this is always ${\log }_2($dimension$)$.

operators

Return the list of frame operators.

pauli_operators

Convert the internal frame operators to Pauli form.

Warning

The conversion to Pauli form can be computationally intensive.

Returns:

The frame operators in Pauli form. Each frame operator is returned as a dictionary mapping Pauli labels to coefficients.

Raises:

QiskitError – when the frame operators could not be converted to Pauli form (e.g. when they are not N-qubit operators).

Methods

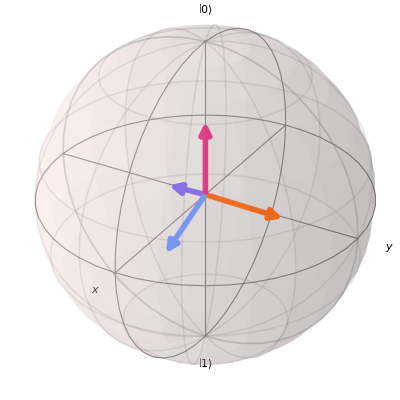
draw_bloch(*, title: str = '', figure: Figure | None = None, axes: Axes | list[Axes] | None = None, figsize: tuple[float, float] | None = None, font_size: float | None = None, colorbar: bool = False) → Figure

Plot the Bloch vector of each effect of the POVM.

>>> import cmath
>>> import numpy as np
>>> from povm_toolbox.quantum_info import SingleQubitPOVM
>>> vecs = np.sqrt(1.0 / 2.0) * np.array(
...     [
...         [1, 0],
...         [np.sqrt(1.0 / 3.0), np.sqrt(2.0 / 3.0)],
...         [np.sqrt(1.0 / 3.0), np.sqrt(2.0 / 3.0) * cmath.exp(2.0j * np.pi / 3)],
...         [np.sqrt(1.0 / 3.0), np.sqrt(2.0 / 3.0) * cmath.exp(4.0j * np.pi / 3)],
...     ]
... )
>>> sic_povm = SingleQubitPOVM.from_vectors(vecs)
>>> sic_povm.draw_bloch()
<Figure size 500x500 with 1 Axes>

(Source code, png, hires.png, pdf)

Parameters:

• title (str) – A string that represents the plot title.

• figure (Figure | None) – User supplied Matplotlib Figure instance for plotting Bloch sphere.

• axes (Axes | list[Axes] | None) – User supplied Matplotlib axes to render the bloch sphere.

• figsize (tuple[float, float] | None) – Figure size in inches. Has no effect if passing ax.

• font_size (float | None) – Size of font used for Bloch sphere labels.

• colorbar (bool) – If True, normalize the vectors on the Bloch sphere and add a colormap to keep track of the norm of the vectors. It can help to visualize the vector if they have a small norm.

Returns:

The resulting figure.

Return type:

Figure

get_bloch_vectors() → ndarray

Compute the Bloch vector of each effect of the POVM.

For a rank-1 POVM, each effect $M_k$ can be written as

$$M_k={\gamma }_k|{\psi }_k⟩⟨{\psi }_k|={\gamma }_k\frac{1}{2}(\mathbb{I}+{\overrightarrow{a}}_k\cdot \overrightarrow{\sigma })$$

where $\overrightarrow{\sigma }$ is the usual Pauli vector and $||{\overrightarrow{a}}_k|{|}^2=1$. We then define the Bloch vector of a rank-1 effect as ${\overrightarrow{r}}_k={\gamma }_k{\overrightarrow{a}}_k$, which uniquely defines the rank-1 effect.

Example:

>>> import cmath
>>> import numpy as np
>>> from povm_toolbox.quantum_info import SingleQubitPOVM
>>> vecs = np.sqrt(1.0 / 2.0) * np.array(
...     [
...         [1, 0],
...         [np.sqrt(1.0 / 3.0), np.sqrt(2.0 / 3.0)],
...         [np.sqrt(1.0 / 3.0), np.sqrt(2.0 / 3.0) * cmath.exp(2.0j * np.pi / 3)],
...         [np.sqrt(1.0 / 3.0), np.sqrt(2.0 / 3.0) * cmath.exp(4.0j * np.pi / 3)],
...     ]
... )
>>> sic_povm = SingleQubitPOVM.from_vectors(vecs)
>>> bloch_vectors = sic_povm.get_bloch_vectors()
>>> print(bloch_vectors)  
[[ 0.          0.          0.5       ]
 [ 0.47140452  0.         -0.16666667]
 [-0.23570226  0.40824829 -0.16666667]
 [-0.23570226 -0.40824829 -0.16666667]]

Returns:

The Bloch vector of all POVM effects.

Raises:

ValueError – if any effect of this POVM has a rank greater than 1.

Return type:

ndarray

Inherited Methods

analysis(hermitian_op: SparsePauliOp | Operator, frame_op_idx: int | set[int] | None = None) → float | dict[int, float] | ndarray

Return the frame coefficients of hermitian_op.

This method implements the analysis operator $A$ of the frame $\{F_k{\}}_k$:

$$A:\mathcal{O}\mapsto \{\mathrm{Tr}\left[F_k\mathcal{O}\right]{\}}_k,$$

where $c_k=\mathrm{Tr}\left[F_k\mathcal{O}\right]$ are called the frame coefficients of the Hermitian operator $\mathcal{O}$.

Parameters:

• hermitian_op (SparsePauliOp | Operator) – a hermitian operator whose frame coefficients to compute.

• frame_op_idx (int | set[int] | None) – label or set of labels indicating which coefficients are queried. If None, all coefficients are queried.

Returns:

Frame coefficients, specified by frame_op_idx, of the Hermitian operator hermitian_op. If a specific coefficient was queried, a float is returned. If a specific set of coefficients was queried, a dictionary mapping labels to coefficients is returned. If all coefficients were queried, an array with all coefficients is returned.

Raises:

• TypeError – when the provided single or sequence of labels frame_op_idx does not have a valid type.

• ValueError – when the dimension of the provided hermitian_op does not match the dimension of the frame operators.

Return type:

float | dict[int, float] | ndarray

classmethod from_vectors(frame_vectors: ndarray) → Self

Initialize a frame from non-normalized bloch vectors.

The non-normalized Bloch vectors are given by $|{\tilde{\psi }}_k⟩=\sqrt{{\gamma }_k}|{\psi }_k⟩$. The resulting frame operators are $F_k={\gamma }_k|{\psi }_k⟩⟨{\psi }_k|$ where ${\gamma }_k$ is the trace of the $k$’th frame operator.

Parameters:

frame_vectors (ndarray) – list of vectors $|\widetilde{{\psi }_k}⟩$. The length of the list corresponds to the number of operators of the frame. Each vector is of shape $(\dim ,)$ where $\dim$ is the dimension of the Hilbert space on which the frame acts.

Returns:

The frame corresponding to the vectors.

Return type:

Self

get_prob(rho: SparsePauliOp | DensityMatrix | Statevector, outcome_idx: LabelT | set[LabelT] | None = None) → float | dict[LabelT, float] | ndarray

Return the outcome probabilities given a state, $\rho$.

Each outcome $k$ is associated with an effect $M_k$ of the POVM. The probability of obtaining the outcome $k$ when measuring a state rho is given by $p_k=\text{Tr}\left[M_k\rho \right]$.

Note

In the frame theory formalism, the mapping $A:\rho \mapsto \{\text{Tr}\left[M_k\rho \right]{\}}_k$ is referred to as the analysis operator, which is implemented by the analysis() method.

Parameters:

• rho (SparsePauliOp | DensityMatrix | Statevector) – the state for which to compute the outcome probabilities.

• outcome_idx (LabelT | set[LabelT] | None) – label or set of labels indicating which outcome probabilities are queried. If None, all outcome probabilities are queried.

Returns:

Probabilities of obtaining the outcome(s) specified by outcome_idx over the state rho. If a specific outcome was queried, a float is returned. If a specific set of outcomes was queried, a dictionary mapping outcomes to probabilities is returned. If all outcomes were queried, an array with all probabilities is returned.

Return type:

float | dict[LabelT, float] | ndarray