Non-IC Measurements¶
This document shows you how to use measurements that are not informationally complete.
Note:
By definition, non-IC POVMs do not span the entire space of Hermitian operators. This means that there exist some observables that are not covered by such POVMs. At present, the post-processor does not check for this when estimating expectation values. This means it is up to the user to ensure that they submits observables compatible with the non-IC POVM.
If the user submits an observable that is not in the span of the POVM, the post-processor will return the expectation value of the observable projected into the span of the POVM. More specifically, this will not give rise to any errors and may go unnoticed by the user.
[1]:
%load_ext autoreload
%autoreload 2
Examples of non-IC POVMs¶
Example of a 4-outcome non-IC POVM¶
[2]:
import numpy as np
from povm_toolbox.library import RandomizedProjectiveMeasurements
# parameters that define a randomized measurement which is not IC. It mixes `Z` and `X` measurements.
angles = np.array(
[0.0, 0.0, np.pi / 2, 0.0],
)
bias = np.array([0.5, 0.5])
ZX_measurement = RandomizedProjectiveMeasurements(
num_qubits=1, angles=angles, bias=bias, seed=592634
)
ZX_measurement.definition().draw_bloch()
[2]:
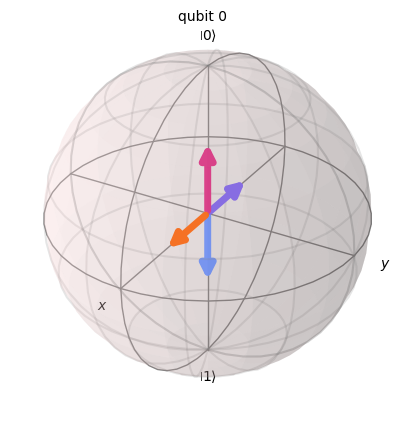
Example of a POVM with some null effects¶
Some POVMs that are usually informationally complete can become non-IC in special cases.
For instance, setting some biases to zero for a randomized measurement will result into some effects being null. This can make the POVM non-IC. The null effects are still being stored, which can prove useful if you follow a convention for the indexing of the outcomes (see the example below).
[3]:
from povm_toolbox.library import LocallyBiasedClassicalShadows
# Define a biased classical shadow measurement with only `Z` and `Y` measurements.
bias = np.array([0.5, 0.0, 0.5]) # order is Z,X,Y
ZY_measurement = LocallyBiasedClassicalShadows(num_qubits=1, bias=bias, seed=587202)
ZY_measurement.definition().draw_bloch()
[3]:
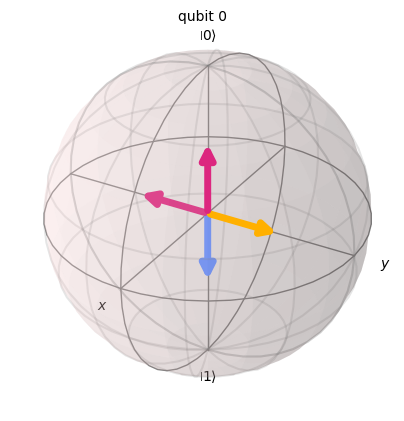
We assume in general that a (locally-biased) classical shadow measurement has 6 outcomes. Therefore, even if we set the bias of a measurement basis to zero, we keep track of the resulting null effects to preserve the number of outcomes and their order.
[4]:
povm = ZY_measurement.definition()[(0,)]
print("Number of outcomes:", povm.num_outcomes)
print("\nPOVM effects:")
for op in povm.operators:
print(op)
Number of outcomes: 6
POVM effects:
Operator([[0.5+0.j, 0. +0.j],
[0. +0.j, 0. +0.j]],
input_dims=(2,), output_dims=(2,))
Operator([[0. +0.j, 0. +0.j],
[0. -0.j, 0.5+0.j]],
input_dims=(2,), output_dims=(2,))
Operator([[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
input_dims=(2,), output_dims=(2,))
Operator([[0.+0.j, 0.+0.j],
[0.-0.j, 0.+0.j]],
input_dims=(2,), output_dims=(2,))
Operator([[2.5000000e-01+0.j , 1.5308085e-17-0.25j],
[1.5308085e-17+0.25j, 2.5000000e-01+0.j ]],
input_dims=(2,), output_dims=(2,))
Operator([[ 2.5000000e-01+0.j , -1.5308085e-17+0.25j],
[-1.5308085e-17-0.25j, 2.5000000e-01+0.j ]],
input_dims=(2,), output_dims=(2,))
Standard IC-POVM¶
For reference, we also consider a standard classical shadows measurement:
[5]:
from povm_toolbox.library import ClassicalShadows
ZXY_measurement = ClassicalShadows(num_qubits=1, seed=301438)
ZXY_measurement.definition().draw_bloch()
[5]:
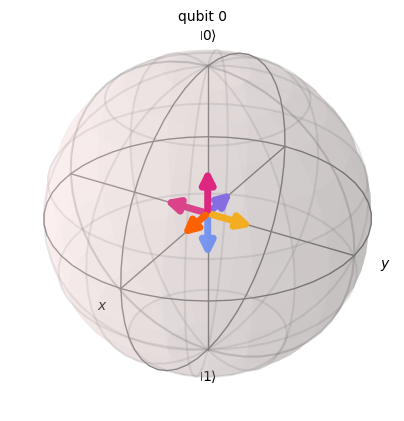
Run experiments¶
Define quantum circuit¶
[6]:
from qiskit.circuit import QuantumCircuit
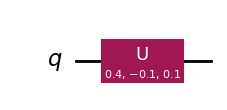
qc = QuantumCircuit(1)
qc.u(0.4, -0.1, 0.1, qubit=0)
qc.draw("mpl")
[6]:
Run the job¶
[7]:
from numpy.random import default_rng
from povm_toolbox.sampler import POVMSampler
from qiskit.primitives import StatevectorSampler as Sampler
sampler = Sampler(seed=default_rng(734567))
povm_sampler = POVMSampler(sampler)
job = povm_sampler.run(
[
(qc, None, None, ZXY_measurement),
(qc, None, None, ZX_measurement),
(qc, None, None, ZY_measurement),
],
shots=4096,
)
Define observable¶
Note that this observable is not fully covered by the ZY_measurement.
[8]:
from qiskit.quantum_info import SparsePauliOp
observable = SparsePauliOp(["X", "Z"], coeffs=[3, 1])
Get the expected value¶
[9]:
from povm_toolbox.post_processor import POVMPostProcessor, dual_from_empirical_frequencies
from qiskit.quantum_info import DensityMatrix
print("Observable: Z + 3*X")
exact_expectation_value = np.real_if_close(DensityMatrix(qc).expectation_value(observable))
print(f"Exact value: {exact_expectation_value}\n")
print("Measurement Estimated value Estimated std Actual error")
print("-------------------------------------------------------------------")
results = job.result()
msmt_strings = [
"Classical shadows",
"Z/X measurement",
"Z/Y measurement",
]
for msmt, pub_result in zip(msmt_strings, results, strict=True):
post_processor = POVMPostProcessor(pub_result)
post_processor.dual = dual_from_empirical_frequencies(post_processor)
exp_value, std = post_processor.get_expectation_value(observable)
print(
f"{msmt:<17} {exp_value:>18.6f} {std:>15.6f}"
f"{abs(exp_value - exact_expectation_value):>15.6f}"
)
Observable: Z + 3*X
Exact value: 2.083479611901199
Measurement Estimated value Estimated std Actual error
-------------------------------------------------------------------
Classical shadows 2.168970 0.076433 0.085491
Z/X measurement 2.064918 0.062295 0.018562
Z/Y measurement 0.925842 0.008414 1.157638
As the observable is not in the span ZY_measurement, it returns an incorrect value (without warning).
To be more specific, the observable \(\mathcal{O} = Z+3*X\) projected into the span of ZY_measurement is \(\hat{\mathcal{O}} = Z\). Therefore, the value returned is the expectation of \(\hat{\mathcal{O}}\).
We can check the value returned by ZY_measurement is actually an estimate of \(\langle Z \rangle_{\rho}\).
[10]:
observable = SparsePauliOp("Z")
print("Observable: Z")
exact_expectation_value = np.real_if_close(DensityMatrix(qc).expectation_value(observable))
print(f"Exact value: {exact_expectation_value}\n")
print("Measurement Estimated value Estimated std Actual error")
print("-------------------------------------------------------------------")
for msmt, pub_result in zip(msmt_strings, results, strict=True):
post_processor = POVMPostProcessor(pub_result)
post_processor.dual = dual_from_empirical_frequencies(post_processor)
exp_value, std = post_processor.get_expectation_value(observable)
print(
f"{msmt:<17} {exp_value:>18.6f} {std:>15.6f}"
f"{abs(exp_value - exact_expectation_value):>15.6f}"
)
Observable: Z
Exact value: 0.9210609940028851
Measurement Estimated value Estimated std Actual error
-------------------------------------------------------------------
Classical shadows 0.914818 0.010650 0.006243
Z/X measurement 0.920608 0.008564 0.000453
Z/Y measurement 0.925842 0.008414 0.004781