注釈

このページは docs/tutorials/11_quantum_convolutional_neural_networks.ipynb から生成されました。

量子畳み込みニューラル・ネットワーク#

1. はじめに#

このチュートリアルでは、Convolutional Neural Network(QCNN)の量子畳み込みニューラルネットワークについて説明します。[1]. 量子回路を使用して畳み込み層とプール層の両方をモデリングすることによって、QiskitにこのようなQCNNを実装します。 このようなネットワークを構築した後、ピクセル化された画像から水平線と垂直線を区別するように学習します。以下のチュートリアルはそれに応じて分割されます。

  1. QCNNとCCNNの違い

  2. QCNN の構成要素

  3. データ生成

  4. QCNN のビルド

  5. QCNNのトレーニング

  6. QCNNのテスト

  7. 参考文献

まず始めに、このチュートリアルで必要となるライブラリーおよびパッケージをインポートします。

[1]:

import json
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
from qiskit import QuantumCircuit
from qiskit.circuit import ParameterVector
from qiskit.circuit.library import ZFeatureMap
from qiskit.quantum_info import SparsePauliOp
from qiskit_algorithms.optimizers import COBYLA
from qiskit_algorithms.utils import algorithm_globals
from qiskit_machine_learning.algorithms.classifiers import NeuralNetworkClassifier
from qiskit_machine_learning.neural_networks import EstimatorQNN
from sklearn.model_selection import train_test_split

algorithm_globals.random_seed = 12345

1. QCNNとCCNNの違い#

1.1 古典的な畳み込みニューラル・ネットワーク#

Classical Convolutional Neural Networks (CCNNs) は、人工のニューラルネットワークのサブクラスであり、与えられた入力の特徴やパターンを決定することができます。 このため、画像認識処理や音声処理などで一般的に使用されています。

フィーチャーを決定するのは 、CCNN で使われている畳み込み層とプーリング層の２種類の層の結果です。

CCNN の例を図 1 に示します。CCNN は、入力画像に猫と犬のどちらが含まれているかを判断するようにトレーニングされています。 そのために、入力画像は一連の畳み込み層 (C) とプーリング層 (P) を交互に通過します。すべての層でパターンが検出され、各パターンが猫または犬に関連付けられます。 全結合層 (FC) は、入力画像が猫か犬かを判断できる出力を提供します。

畳み込み層はカーネルを利用し、特定の入力の特徴量やパターンを決定することができます。この例は画像の特徴量検出であり、異なる層が入力画像中の特定のパターンを検出します。これは図1に示されており、 \(l^{th}\) 層は \(ij\) 平面に沿って特徴やパターンを認識します。そして、学習プロセスにおいて、そのような特徴量を与えられた出力と関連付けることができ、このプロセスを用いてデータセットを学習させることができます。

一方、プーリング層は入力データの次元を減らし、CCNNの計算コストと学習パラメーターの量を減らすことができます。CCNNの模式図を以下に示します。

CCNNの詳細については、 [2] を参照してください。

Screenshot%202022-08-09%20at%2017.03.09.png 図1. 猫と犬の画像の間を分類するためにCCNNを使用する概略的なデモンストレーション。ここでは、いくつかの畳み込み層とプーリング層が適用されており、プーリング層の使用により、すべての次元が減少していることがわかります。CCNNの出力は、入力画像が猫であるか犬であるかを決定します。画像は[1]の形から得られました。

1.2 量子畳み込みニューラル・ネットワーク#

量子畳み込みニューラルネットワーク（QCNN）は、CCNNと同様の動作をします。まず、QiskitのZFeatureMapやZZFeatureMapなど、circuit ライブラリーにある所定の特徴量マップを用いて、画素化した画像を量子回路にエンコードします。

画像を符号化した後、次のセクションで定義するように、畳み込み層とプーリング層を交互に適用します。これらの層を交互に適用することで、回路の次元を減らし、1つの量子ビットを残すことができます。そして、この残った1つの量子ビットの出力を測定することで、入力画像を分類することができます。

量子畳み込み層は一連の2量子ビットユニタリー演算子で構成され、回路内の量子ビットの関係を認識し決定します。このユニタリーゲートは次のセクションで定義されます。

量子プーリング層では、古典的に行われているような、回路の次元、すなわち量子ビットの数を減らすようなことはできません。その代わりに、ある時点まで各量子ビットの演算を行い、特定の層で特定の量子ビットを無視することによって、量子ビット数を減らします。特定の量子ビットの演算を停止するこれらの層を、私たちは「プーリング層」と呼んでいます。プーリング層の詳細については、次のセクションでさらに説明します。

QCNNでは各層にパラメーター化された回路があり、各層のパラメーターを調整することで出力結果を変化させられます。QCNNを学習する際には、これらのパラメーターを調整し、QCNNの損失関数を減少させます。

4量子ビットのQCNNの簡単な例を以下に示します。

figure2.png

図2: 4つの量子ビットを含むQCNNの例。最初の畳み込み層は全ての量子ビットに作用します。これに最初のプーリング層が続き、最初の2量子ビットを無視することによって、QCNNの次元を4量子ビットから2量子ビットに削減します。次に2番目の畳み込み層が、QCNNでまだ使用されている2つの量子ビットの間の特徴を検出し、続いて別のプーリング層が次元を2量子ビットから1量子ビットに削減し、これが我々の出力量子ビットとなります。

2. QCNN の構成要素#

このチュートリアルのセクション 1 で議論したように、CCNN は畳み込み層とプーリング層の両方を含むことになります。ここでは、量子回路に適用されるゲートという観点から QCNN のためにこれらの層を定義し、4量子ビットのための各層の例を示します。

これらの各層は、損失関数を最小化し、QCNNが水平線と垂直線を分類するように学習プロセスを通じて調整されるパラメーターを含んでいます。

理論的には、我々のネットワークの畳み込み層とプーリング層の両方に、任意のパラメーター化された回路を適用することができます。例えば、[2] では、Gellmann行列(Pauli行列の3次元一般化) が、1組の量子ビットに作用する各ユニタリーゲートの生成子として使用されています。

ここでは、異なるアプローチとして、[3]で提案された2量子ビットのユニタリーに基づいてパラメーター化された回路を構成します。これは、 \(U(4)\) のすべてのユニタリー行列が、以下のように分解できることを述べています。

\[U = (A_1 \otimes A_2) \cdot N(\alpha, \beta, \gamma) \cdot (A_3 \otimes A_4)\]

ここで、 \(A_j \in \text{SU}(2)\) 、 \(\otimes\) はテンソル積、 \(N(\alpha, \beta, \gamma) = exp(i [\alpha \sigma_x\sigma_x + \beta \sigma_y\sigma_y + \gamma \sigma_z\sigma_z ])\) 、ここで \(\alpha, \beta, \gamma\) は調整できるパラメーターです。

このことから、各ユニタリーは15個のパラメーターに依存しており、QCNNがHilbert空間全体をカバーするためには、我々のQCNNの各ユニタリーはそれぞれ15個のパラメーターを含んでいなければならないことがわかります。

この大量のパラメーターを調整するのは難しく、学習時間が長くなってしまいます。この問題を克服するために、私たちはansatzをヒルベルト空間の特定の部分空間に制限し、2量子ビットユニタリーゲートを \(N(\alpha, \beta, \gamma)\) として定義します。これらの2量子ビットのユニタリーは[3]に見られるように、QCNNの各層で隣接するすべての量子ビットに適用されるもので、以下のようになります。

QCNN を特定の部分空間に限定することで、最適解が含まれない可能性があり、QCNN の精度が低下することに注意してください。このチュートリアルの目的では、このパラメーター化された回路を使ってQCNNの学習時間を短縮することにします。

circuit2.png

図 3: \(N(\alpha, \beta, \gamma) = exp(i[\alpha \sigma_x\sigma_x + \beta \sigma_y\sigma_y + \gamma \sigma_z\sigma_z ] )\) のパラメーター化された 2 量子ビット ユニタリー回路。 [3] に見られるように、ここで \(\alpha = \frac{\pi}{2} - 2\theta\), \(\beta = 2\phi - \frac{\pi}{2}\) と \(\gamma = \frac{\pi}{2} - 2\lambda\) が回路に見られます。 この 2 量子ビットユニタリーは、特徴量マップ内の隣接するすべての量子ビットに適用されます。

2.1 畳み込み層#

このチュートリアルの次のステップは、QCNNの畳み込み層を定義することです。これらの層は、データが特徴量マップの使用によりエンコードされた後、量子ビットに適用されます。

そのためには、まず、畳み込み層とプーリング層の作成に使用するパラメーター化されたユニタリーゲートを決定する必要があります。

[2]:

# We now define a two qubit unitary as defined in [3]
def conv_circuit(params):
    target = QuantumCircuit(2)
    target.rz(-np.pi / 2, 1)
    target.cx(1, 0)
    target.rz(params[0], 0)
    target.ry(params[1], 1)
    target.cx(0, 1)
    target.ry(params[2], 1)
    target.cx(1, 0)
    target.rz(np.pi / 2, 0)
    return target


# Let's draw this circuit and see what it looks like
params = ParameterVector("θ", length=3)
circuit = conv_circuit(params)
circuit.draw("mpl", style="clifford")

[2]:
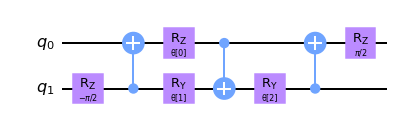
../_images/tutorials_11_quantum_convolutional_neural_networks_19_0.png

さて、これらのユニタリーを定義したところで、QCNNの畳み込み層の関数を作成することにします。これを行うには、以下の conv_layer 関数で見られるように、隣接する量子ビットに2量子ビットのユニタリーを適用します。

最初に 2 量子ビットユニタリーをすべての偶数量子ビットのペアに適用し、続いて循環結合方式で奇数の量子ビットのペアに適用することに注意してください。つまり、隣接する量子ビットが結合されるのと同様に、最初と最後の量子ビットもユニタリーゲートを通して結合されるのです。

なお、プロットする際の便宜上、量子回路にバリアーを追加していますが、実際のQCNNでは不要であり、以下の回路から削除することが可能です。

[3]:

def conv_layer(num_qubits, param_prefix):
    qc = QuantumCircuit(num_qubits, name="Convolutional Layer")
    qubits = list(range(num_qubits))
    param_index = 0
    params = ParameterVector(param_prefix, length=num_qubits * 3)
    for q1, q2 in zip(qubits[0::2], qubits[1::2]):
        qc = qc.compose(conv_circuit(params[param_index : (param_index + 3)]), [q1, q2])
        qc.barrier()
        param_index += 3
    for q1, q2 in zip(qubits[1::2], qubits[2::2] + [0]):
        qc = qc.compose(conv_circuit(params[param_index : (param_index + 3)]), [q1, q2])
        qc.barrier()
        param_index += 3

    qc_inst = qc.to_instruction()

    qc = QuantumCircuit(num_qubits)
    qc.append(qc_inst, qubits)
    return qc


circuit = conv_layer(4, "θ")
circuit.decompose().draw("mpl", style="clifford")

[3]:
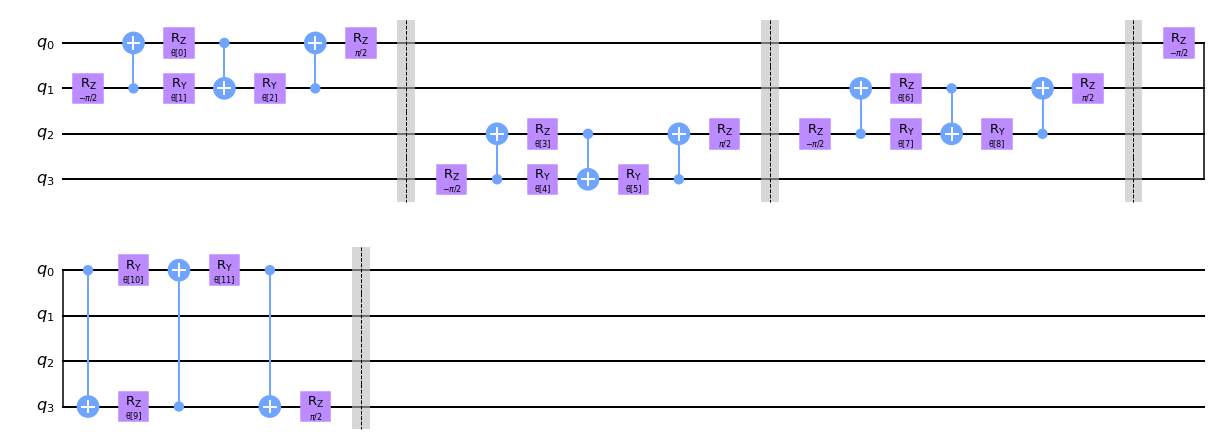
../_images/tutorials_11_quantum_convolutional_neural_networks_21_0.png

2.2 プーリング層#

プーリング層の目的は、以前に学習したデータからできるだけ多くの情報を保持しながら、量子回路の次元を小さくすること、すなわち回路の量子ビットの数を減らすことです。量子ビットの数を減らすことは、QCNNが学習する必要のあるパラメーターの数が減るため、回路全体の計算コストも減らすことができます。

しかし、量子回路に含まれる量子ビットの数を単純に減らすことはできません。このため、古典的なアプローチとは異なる方法でプーリング層を定義する必要があります。

回路内の量子ビットの数を「人為的に」減らすために、まずシステム内の \(N\) 個の量子ビットのペアを作ることから始めます。

最初にすべての量子ビットをペアリングした後、前述のように一般化された2量子ビットユニタリーを各ペアに適用します。この2量子ビットのユニタリーを適用した後、ニューラルネットワークの残りの部分では、各ペアの量子ビットから1つの量子ビットを無視します。

この層は、まずユニタリー回路を適用して、1つの量子ビットの情報を別の量子ビットに符号化し、残りの回路では一方の量子ビットを無視し、それに対していかなる演算や測定も行わないことで、2つの量子ビットの情報を1つに「結合」する全体効果を持ちます。

プーリング層の次元を減らすために動的回路を適用することも可能であることに留意してください。これは、回路内の特定の量子ビットの測定を行い、我々のプーリング層に中間的な古典的なフィードバック・ループを持たせることになります。これらの測定を適用することによって、回路の次元を減らすこともできるでしょう。

このチュートリアルでは、前者のアプローチを適用し、各プーリング層の量子ビットを無視します。このアプローチを用いて、私たちは \(N\) 量子回路の次元を \(N/2\) に変換するQCNNプーリング層を作成します。

そのために、まず、2量子ビット系を1量子ビットに変換する2量子ビットユニタリーを定義します。

[4]:

def pool_circuit(params):
    target = QuantumCircuit(2)
    target.rz(-np.pi / 2, 1)
    target.cx(1, 0)
    target.rz(params[0], 0)
    target.ry(params[1], 1)
    target.cx(0, 1)
    target.ry(params[2], 1)

    return target


params = ParameterVector("θ", length=3)
circuit = pool_circuit(params)
circuit.draw("mpl", style="clifford")

[4]:
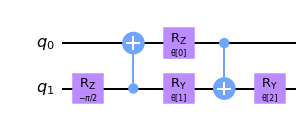
../_images/tutorials_11_quantum_convolutional_neural_networks_24_0.png

この2量子ビットのユニタリー回路を適用した後、その後の層では第1量子ビット (q0) を無視し、第2量子ビット (q1) のみをQCNNで使用します。

この2量子ビットのプーリング層を異なる量子ビットのペアに適用し、N量子ビットのプーリング層を作成します。例として、4つの量子ビットについてプロットしてみます。

[5]:

def pool_layer(sources, sinks, param_prefix):
    num_qubits = len(sources) + len(sinks)
    qc = QuantumCircuit(num_qubits, name="Pooling Layer")
    param_index = 0
    params = ParameterVector(param_prefix, length=num_qubits // 2 * 3)
    for source, sink in zip(sources, sinks):
        qc = qc.compose(pool_circuit(params[param_index : (param_index + 3)]), [source, sink])
        qc.barrier()
        param_index += 3

    qc_inst = qc.to_instruction()

    qc = QuantumCircuit(num_qubits)
    qc.append(qc_inst, range(num_qubits))
    return qc


sources = [0, 1]
sinks = [2, 3]
circuit = pool_layer(sources, sinks, "θ")
circuit.decompose().draw("mpl", style="clifford")

[5]:
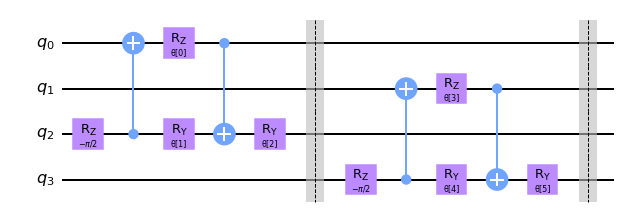
../_images/tutorials_11_quantum_convolutional_neural_networks_26_0.png

この特定の例では、4つの量子ビット回路の次元を最後の2つの量子ビットにまで縮小します。これらの量子ビットは次の層で使用され、最初の2つはQCNNの残りの部分では無視されます。

3. データ生成#

CCNN の一般的な用途の 1 つは画像分類器です。CCNNは、畳み込み層の特徴量マップを利用して、ピクセル化された画像の特定の特徴やパターン (直線や曲線など) を検出することができます。これらの特徴量間の関係を学習することで、手書きの数字を簡単に分類し、ラベル付けすることができます。

古典的なCNNは特徴やパターンを簡単に認識できるため、QCNNも与えられた画素画像のパターンや特徴を判断し、2つの異なるパターンの間で分類できるように訓練します。

データセットを単純化するために、我々は2×4ピクセルの画像のみを考慮します。QCNNが識別するために訓練するパターンは、水平または垂直の線であり、画像内のどこにでも配置でき、ノイズの多い背景と一緒に配置できます。

まず、このデータセットを生成することから始めます。 「水平」または「垂直」な線を作成するために、ピクセル値を \(\frac{\pi}{2}\) に割り当てます。これは、ピクセル化された画像中の線を表現します。他のピクセルには \(0\) から \(\frac{\pi}{4}\) の間のランダムな値を割り当てて、ノイズの多い背景を作成します。

なお、データセットを作成する際には、画像のトレーニングセットとテストセットに分割する必要があり、それぞれニューラルネットワークのトレーニングとテストを行うデータセットとなります。

また、QCNNが2つのパターンを区別することを学習できるように、データセットにラベル付けする必要があります。この例では、横線のある画像に-1、縦線のある画像に+1のラベルを付けます。

[6]:

def generate_dataset(num_images):
    images = []
    labels = []
    hor_array = np.zeros((6, 8))
    ver_array = np.zeros((4, 8))

    j = 0
    for i in range(0, 7):
        if i != 3:
            hor_array[j][i] = np.pi / 2
            hor_array[j][i + 1] = np.pi / 2
            j += 1

    j = 0
    for i in range(0, 4):
        ver_array[j][i] = np.pi / 2
        ver_array[j][i + 4] = np.pi / 2
        j += 1

    for n in range(num_images):
        rng = algorithm_globals.random.integers(0, 2)
        if rng == 0:
            labels.append(-1)
            random_image = algorithm_globals.random.integers(0, 6)
            images.append(np.array(hor_array[random_image]))
        elif rng == 1:
            labels.append(1)
            random_image = algorithm_globals.random.integers(0, 4)
            images.append(np.array(ver_array[random_image]))

        # Create noise
        for i in range(8):
            if images[-1][i] == 0:
                images[-1][i] = algorithm_globals.random.uniform(0, np.pi / 4)
    return images, labels

Let’s now create our dataset below and split it into our test and training datasets. We pass a random_state so the split will be the same each time this notebook is run so the final results do not vary.

[7]:

images, labels = generate_dataset(50)

train_images, test_images, train_labels, test_labels = train_test_split(
    images, labels, test_size=0.3, random_state=246
)

データセットでいくつかの例を見てみましょう。

[8]:

fig, ax = plt.subplots(2, 2, figsize=(10, 6), subplot_kw={"xticks": [], "yticks": []})
for i in range(4):
    ax[i // 2, i % 2].imshow(
        train_images[i].reshape(2, 4),  # Change back to 2 by 4
        aspect="equal",
    )
plt.subplots_adjust(wspace=0.1, hspace=0.025)
../_images/tutorials_11_quantum_convolutional_neural_networks_34_0.png

見ての通り、各画像には縦線と横線があり、QCNNはそれを区別する方法を学習します。さて、データセットが構築できたので、次はQCNNの構成要素について議論し、モデルを構築する番です。

4. QCNNのモデリング#

さて、両方の畳み込み層を定義したので、次は QCNN を構築する番であり、プーリング層と畳み込み層を交互に構成します。

データセットの画像は8ピクセルであるため、QCNNでは8個の量子ビットを使用することにします。

我々は、特徴量マップを適用することによってデータセットをQCNNにエンコードします。特徴量マップは、ZFeatureMapやZZFeatureMapなど、Qiskitに組み込まれている特徴量マップのいずれかを使用して作成することができます。

このデータセットに対していくつかの異なる特徴量マップを分析した結果、QCNN は Z feature mapを使用した場合に最も高い精度が得られることがわかりました。したがって、このチュートリアルの残りの部分では、以下に示すZ feature map を使用することにします。

[9]:

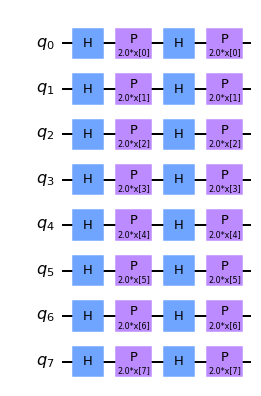
feature_map = ZFeatureMap(8)
feature_map.decompose().draw("mpl", style="clifford")

[9]:
../_images/tutorials_11_quantum_convolutional_neural_networks_38_0.png

QCNNの関数を作成します。この関数は、以下の概略図に見られるように、畳み込み層とプーリング層を3つ交互に含みます。プーリング層の使用により、我々はQCNNの次元を8量子ビットから1量子ビットに減少させることができます。

Screenshot%202022-08-10%20at%2021.42.39.png

水平線と垂直線の画像データセットを分類するために、最後の量子ビットのパウリZ演算子の期待値を測定します。得られた値が+1または-1であることに基づいて、入力画像に水平または垂直な線が含まれていると結論付けることができます。

5. QCNNのトレーニング#

次のステップは、学習データを使ってモデルを構築することです。

このシステムを分類するために、出力回路から計測を行います。この測定値により、入力データが縦線か横線かを分類します。

このチュートリアルで選んだ測定値は \(<Z>\) 、すなわち、最終的な量子ビットに対するPauli Z量子ビットの期待値です。この期待値を測定すると、+1または-1が得られ、それぞれ垂直線または水平線に対応します。

[10]:

feature_map = ZFeatureMap(8)

ansatz = QuantumCircuit(8, name="Ansatz")

# First Convolutional Layer
ansatz.compose(conv_layer(8, "c1"), list(range(8)), inplace=True)

# First Pooling Layer
ansatz.compose(pool_layer([0, 1, 2, 3], [4, 5, 6, 7], "p1"), list(range(8)), inplace=True)

# Second Convolutional Layer
ansatz.compose(conv_layer(4, "c2"), list(range(4, 8)), inplace=True)

# Second Pooling Layer
ansatz.compose(pool_layer([0, 1], [2, 3], "p2"), list(range(4, 8)), inplace=True)

# Third Convolutional Layer
ansatz.compose(conv_layer(2, "c3"), list(range(6, 8)), inplace=True)

# Third Pooling Layer
ansatz.compose(pool_layer([0], [1], "p3"), list(range(6, 8)), inplace=True)

# Combining the feature map and ansatz
circuit = QuantumCircuit(8)
circuit.compose(feature_map, range(8), inplace=True)
circuit.compose(ansatz, range(8), inplace=True)

observable = SparsePauliOp.from_list([("Z" + "I" * 7, 1)])

# we decompose the circuit for the QNN to avoid additional data copying
qnn = EstimatorQNN(
    circuit=circuit.decompose(),
    observables=observable,
    input_params=feature_map.parameters,
    weight_params=ansatz.parameters,
)

[11]:

circuit.draw("mpl", style="clifford")

[11]:
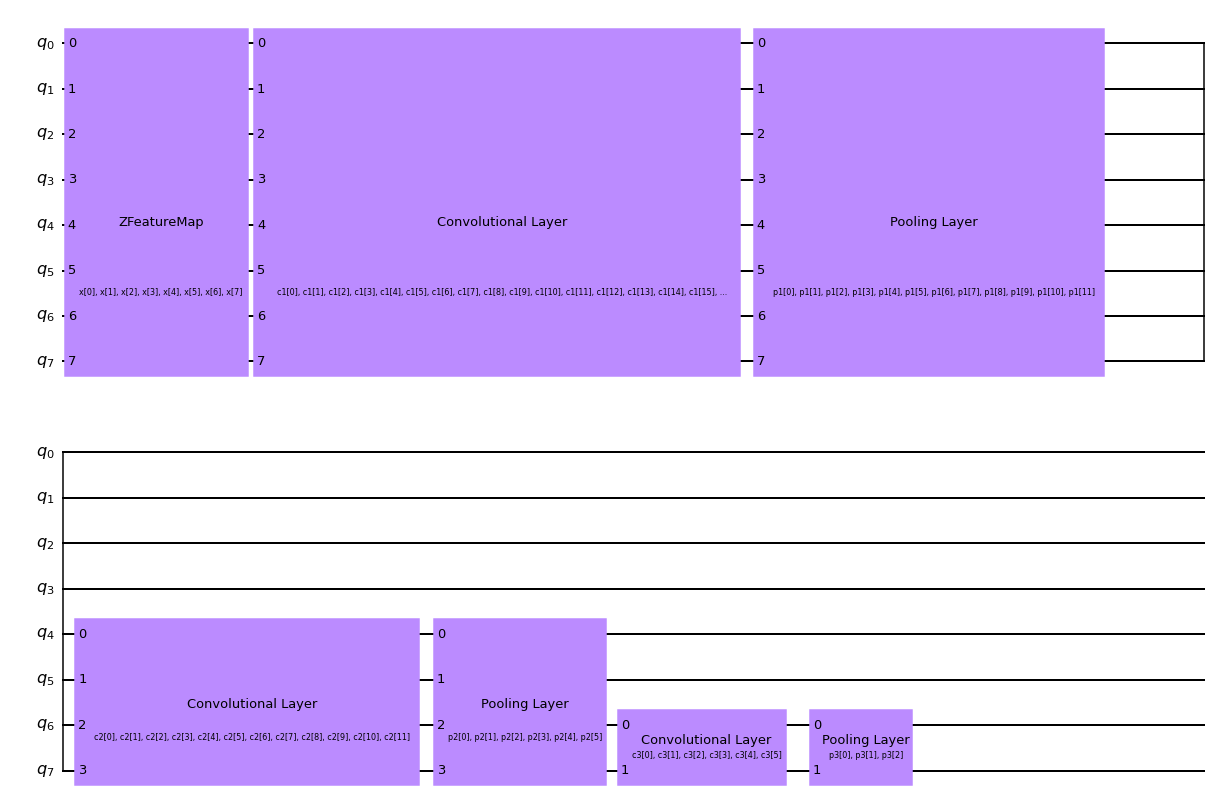
../_images/tutorials_11_quantum_convolutional_neural_networks_45_0.png

また、モデルの学習時に使用するコールバック関数も定義します。これにより、学習過程における各反復ごとの損失関数を表示し、プロットすることができます。

[12]:

def callback_graph(weights, obj_func_eval):
    clear_output(wait=True)
    objective_func_vals.append(obj_func_eval)
    plt.title("Objective function value against iteration")
    plt.xlabel("Iteration")
    plt.ylabel("Objective function value")
    plt.plot(range(len(objective_func_vals)), objective_func_vals)
    plt.show()

この例では、分類器の学習にCOBYLAオプティマイザーを使用します。これは、分類機械学習アルゴリズムによく使用される数値最適化手法です。

そして、上記で作成したQCNNのコールバック関数、オプティマイザー、演算子をQiskit Machine Learningに内蔵されたニューラルネットワーク分類器に配置し、それを使ってモデルの学習を行います。

モデルの学習には長い時間がかかる可能性があるため、すでにいくつかの反復で事前学習したモデルがあり、事前学習済みの重みを保存してあります。 initial_point に学習済みの重みのベクトルを設定することで、その時点から学習を継続することにします。

[13]:

with open("11_qcnn_initial_point.json", "r") as f:
    initial_point = json.load(f)

classifier = NeuralNetworkClassifier(
    qnn,
    optimizer=COBYLA(maxiter=200),  # Set max iterations here
    callback=callback_graph,
    initial_point=initial_point,
)

この分類器を作成した後、学習データセットと各画像に対応するラベルを用いてQCNNを学習することができます。コールバック関数を定義したので、反復ごとのシステムの全体的な損失をプロットします。

QCNNの学習には時間がかかるので、気長に待ちましょう。

[14]:

x = np.asarray(train_images)
y = np.asarray(train_labels)

objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
classifier.fit(x, y)

# score classifier
print(f"Accuracy from the train data : {np.round(100 * classifier.score(x, y), 2)}%")
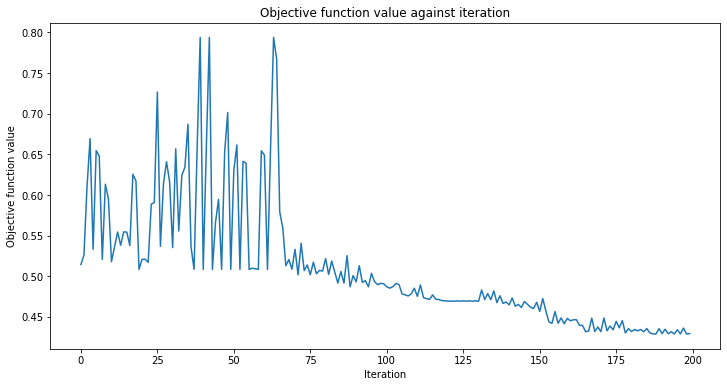
../_images/tutorials_11_quantum_convolutional_neural_networks_51_0.png 
Accuracy from the train data : 97.14%

上図からわかるように、QCNN はゆっくりと収束するので、initial_point は既に最適解に近いものでした。次のステップは、このQCNNがテスト画像データセットに見られるデータを分類できるかどうかを判断することです。

6. QCNNのテスト#

データセットの構築と学習が完了したら、今度はQCNNがテストデータセット以外の画像を予測できるかどうかをテストしてみましょう。

[15]:

y_predict = classifier.predict(test_images)
x = np.asarray(test_images)
y = np.asarray(test_labels)
print(f"Accuracy from the test data : {np.round(100 * classifier.score(x, y), 2)}%")

# Let's see some examples in our dataset
fig, ax = plt.subplots(2, 2, figsize=(10, 6), subplot_kw={"xticks": [], "yticks": []})
for i in range(0, 4):
    ax[i // 2, i % 2].imshow(test_images[i].reshape(2, 4), aspect="equal")
    if y_predict[i] == -1:
        ax[i // 2, i % 2].set_title("The QCNN predicts this is a Horizontal Line")
    if y_predict[i] == +1:
        ax[i // 2, i % 2].set_title("The QCNN predicts this is a Vertical Line")
plt.subplots_adjust(wspace=0.1, hspace=0.5)

Accuracy from the test data : 93.33%
../_images/tutorials_11_quantum_convolutional_neural_networks_55_1.png

上図から、私たちのQCNNは水平線と垂直線を分類できることがわかります。おめでとうございます。量子回路と量子畳み込み層と量子プーリング層を使って、あなたは量子畳み込みニューラルネットワークを構築しました!

7. 参考文献#

[1] Cong, I., Choi, S. & Lukin, M.D. Quantum convolutional neural networks. Nat. Phys. 15, 1273–1278 (2019). https://doi.org/10.1038/s41567-019-0648-8

[2] IBM Convolutional Neural Networks https://www.ibm.com/cloud/learn/convolutional-neural-networks

[3] Vatan, Farrokh, and Colin Williams. “Optimal quantum circuits for general two-qubit gates.” Physical Review A 69.3 (2004): 032315.

[16]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

SoftwareVersion
qiskit1.0.0.dev0+737f21b
qiskit_algorithms0.3.0
qiskit_machine_learning0.8.0
System information
Python version3.9.7
Python compilerGCC 7.5.0
Python builddefault, Sep 16 2021 13:09:58
OSLinux
CPUs2
Memory (Gb)5.792198181152344
Thu Dec 14 13:53:25 2023 EST

This code is a part of Qiskit

© Copyright IBM 2017, 2023.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.