Note

Cette page a été générée à partir de docs/tutorials/11_quantum_convolutional_neural_networks.ipynb.

Le réseau neuronal convolutif quantique

1. Introduction

Tout au long de ce tutoriel, nous discutons d’un réseau neuronal convolutif quantique (QCNN), proposé pour la première fois par Cong et. al. [1]. Nous implémentons un tel QCNN sur Qiskit en modélisant à la fois les neurones convolutionnels et les neurones de mise en commun à l’aide d’un circuit quantique. Après avoir construit un tel réseau, nous l’entraînons pour différencier les lignes horizontales et verticales d’une image pixélisée. Le tutoriel suivant est donc divisé en conséquence;

1. Différences entre un QCNN et un CCNN

2. Éléments d’un QCNN

3. Génération de données

4. Construction d’un QCNN

5. Entraîner notre QCNN

6. Tester notre QCNN

7. Références

Nous commençons par importer les bibliothèques et les paquets dont nous aurons besoin pour ce tutoriel.

import json
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
from qiskit import QuantumCircuit
from qiskit.circuit import ParameterVector
from qiskit.circuit.library import ZFeatureMap
from qiskit.quantum_info import SparsePauliOp
from qiskit_algorithms.optimizers import COBYLA
from qiskit_algorithms.utils import algorithm_globals
from qiskit_machine_learning.algorithms.classifiers import NeuralNetworkClassifier
from qiskit_machine_learning.neural_networks import EstimatorQNN
from sklearn.model_selection import train_test_split

algorithm_globals.random_seed = 12345

1. Différences entre un QCNN et un CCNN

1.1 Réseau neuronal convolutif classique

Les réseaux neuronaux convolutifs classiques (CCNNs) sont une sous-classe des réseaux de neurones artificiels qui ont la capacité de déterminer des caractéristiques et des motifs particuliers pour une entrée donnée. De ce fait, ils sont couramment utilisés pour la reconnaissance d’images et le traitement audio.

La capacité de déterminer les caractéristiques est le résultat des deux types de couches utilisées dans un CCNN, la couche convolutive et la couche de mise en commun.

On peut voir un exemple de CCNN dans la Figure 1, où un CCNN est entraîné pour déterminer si une image contient soit un chat, soit un chien. Pour cela, l’image passe à travers une série alernante de couches convolutives (C) et de mise en commun (P), qui permettent de détecter des motifs et de les associer à un chat ou à un chien. La couche entièrement connectée (FC) nous fournit un résultat qui nous permet de déterminer si l’image était un chat ou un chien.

La couche convolutionnaire utilise un noyau qui peut déterminer les caractéristiques et les motifs d’une entrée particulière. Un exemple de cette fonction est la détection des fonctions dans une image, où différentes couches détectant des motifs particuliers dans l’image d’entrée. Ceci est illustré à la figure 1, où la couche :math:` l ^{th}` reconnaît les caractéristiques et les motifs le long du plan :math:` ij. Il peut ensuite associer de telles fonctions à une sortie donnée dans le processus de formation, et peut utiliser ce processus pour entraîner le jeu de données.

D’autre part, une couche de mise en commun réduit la dimensionnalité des données, ce qui réduit le coût de calcul et la quantité de paramètres d’apprentissage dans le CCNN. On peut voir ci-dessous le schéma d’un CCNN.

Pour plus d’informations sur les CCNN, voir [2].

Figure 1. Une démonstration schématique de l’utilisation d’un CCNN pour différencier les images d’un chat et d’un chien. Ici, nous voyons l’application de plusieurs couches convolutives et de mise en commun, qui diminuent en dimension à cause des couches de mise en commun. Le résultat du CCNN détermine si l’image était un chat ou un chien. Image originelle [1].

1.2. Réseau neuronal convolutif quantique

Les réseaux neuronaux convolutifs quantiques (QCNN) se comportent de la même manière que les CCNNs. Tout d’abord, nous encodons notre image pixelée dans un circuit quantique à l’aide d’une carte de fonction, telle que ZFeatureMap, ZZFeatureMap ou d’autres disponibles dans la bibliothèque de circuits Qiskit.

Après avoir encodé notre image, nous appliquons des couches alternatives de convolution et de mise en commun, comme décrit dans la section suivante. En appliquant ces couches alternées, nous réduisons la dimensionnalité de notre circuit jusqu’à ce qu’il nous reste un seul qubit. Nous pouvons alors classifier notre image en mesurant le qubit restant.

La couche convolutive quantique se compose d’une série de deux opérateurs quantiques unitaires, qui reconnaissent et déterminent les relations entre les qubits de notre circuit. Ces opérateurs unitaires sont défini ci-dessous dans la section suivante.

Pour la couche de mise en commun quantique, nous ne pouvons pas faire de même, comme c’est fait classiquement pour réduire la dimension, c’est-à-dire le nombre de qubits dans notre circuit. Au lieu de cela, nous réduisons le nombre de qubits en effectuant des opérations sur chacun d’entre eux jusqu’à un point spécifique, puis nous ignorons certains qubits dans une couche spécifique. Ce sont ces couches où nous arrêtons les opérations sur certains qubits que nous appelons notre « couche de mise en commun ». Les détails de la mise en commun sont discutés plus en détail dans la section suivante.

Dans un QCNN, chaque couche contient des circuits paramétrés, ce qui signifie que nous modifions nos résultats en ajustant les paramètres de chaque couche. Lors de l’apprentissage de notre QCNN, ce sont ces paramètres qui sont ajustés pour réduire la fonction de perte du QCNN.

Un exemple simple d’un QCNN à quatre qubits peut être vu ci-dessous.

Figure 2: Exemple QCNN contenant quatre qubits. La première couche convolutionnaire agit sur tous les qubits. Ceci est suivi par la première couche de mise en commun, ce qui réduit la dimensionnalité de QCNN de quatre qubits à deux qubits en disconcernant les deux premiers. La seconde couche Convolutionnaire détecte alors les caractéristiques entre les deux qubits toujours en cours d’utilisation sur la QCNN, suivie d’une autre couche de mise en commun, ce qui réduit la dimensionnalité de deux qubits à un, ce qui sera notre qubit de sortie.

2. Éléments d’un QCNN

Comme nous l’avons vu à la section 1 de ce tutoriel, un NCCNN contiendra à la fois des couches convolutionnaires et des couches de mise en commun. Ici, nous définissons ces couches pour QCNN en termes de portes appliquées à un circuit quantique et montrons un exemple pour chaque couche pour 4 qubits.

Chacune de ces couches contiendra des paramètres qui seront réglés tout au long du processus de formation afin de minimiser la fonction de perte et de former la QCNN à classer entre les lignes horizontales et verticales.

En théorie, on pourrait appliquer n’importe quel circuit paramétré pour les couches conévolutionnaires et de mise en commun de notre réseau. Par exemple, en [2], les matrices de Gellmann (qui sont la généralisation tridimensionnelle des matrices de Pauli) sont utilisées comme générateurs pour chaque porte unitaire agissant sur une paire de qubits.

Here, we take a different approach and form our parametrized circuit based on the two qubit unitary as proposed in [3]. This states that every unitary matrix in \(U(4)\) can be decomposed such that

\[U = (A_1 \otimes A_ 2) \cdot N (\alpha, \beta, \gamma) \cdot (A_3 \otimes A_ 4)\]

where \(A_j \in \text{SU}(2)\), \(\otimes\) is the tensor product, and \(N(\alpha, \beta, \gamma) = exp(i[\alpha \sigma_x\sigma_x + \beta \sigma_y\sigma_y + \gamma \sigma_z\sigma_z ])\), where \(\alpha, \beta, \gamma\) are the parameters that we can adjust.

A partir de cela, il est évident que chaque unitaire dépend de 15 paramètres et implique que pour que le QCNN puisse couvrir l’ensemble de l’espace de Hilbert, chaque unitaire de notre QCNN doit contenir 15 paramètres chacun.

L’optimisation de cette grande quantité de paramètres serait difficile et mènerait à de longues périodes de formation. Pour surmonter ce problème, nous limitons notre ansatz à un sous-espace particulier de l’espace de Hilbert et nous définissons la porte unitaire de deux qubits sous le nom de :math:` N (alpha, beta, gamma) `. Ces deux groupes de qubit, comme on peut le voir dans le [3] , peuvent être vus ci-dessous et sont appliqués à tous les qubits voisins de chacune des couches de la QCNN.

Note that by only using \(N(\alpha, \beta, \gamma)\) as our two qubit unitary for the parametrized layers, we are restricting our QCNN to a particular subspace, one in which the optimal solution may not be contained in and reducing the accuracy of the QCNN. For the purpose of this tutorial, we will use this parametrized circuit to decrease the training time of our QCNN.

Figure 3: Parametrized two qubit unitary circuit for \(N(\alpha, \beta, \gamma) = exp(i[\alpha \sigma_x\sigma_x + \beta \sigma_y\sigma_y + \gamma \sigma_z\sigma_z ])\) as seen in [3], where \(\alpha = \frac{\pi}{2} - 2\theta\), \(\beta = 2\phi - \frac{\pi}{2}\) and \(\gamma = \frac{\pi}{2} - 2\lambda\) as seen in the circuit. This two qubit unitary will be applied to all neighboring qubits in our feature map.

2.1 Convolutional Layer

L’étape suivante de ce tutoriel est de définir les couches convolutionnelles de notre QCNN. Ces couches sont ensuite appliquées aux qubits après que les données ont été encodées à l’aide de la carte de fonction.

Pour ce faire, nous devons d’abord déterminer une grille unitaire paramétrée, qui sera utilisée pour créer nos couches convolutionnaires et de mise en commun.

# We now define a two qubit unitary as defined in [3]
def conv_circuit(params):
    target = QuantumCircuit(2)
    target.rz(-np.pi / 2, 1)
    target.cx(1, 0)
    target.rz(params[0], 0)
    target.ry(params[1], 1)
    target.cx(0, 1)
    target.ry(params[2], 1)
    target.cx(1, 0)
    target.rz(np.pi / 2, 0)
    return target


# Let's draw this circuit and see what it looks like
params = ParameterVector("θ", length=3)
circuit = conv_circuit(params)
circuit.draw("mpl", style="clifford")

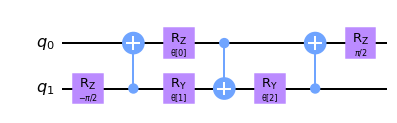
Now that we have defined these unitaries, it is time to create a function for the convolutional layer in our QCNN. To do so, we apply the two qubit unitary to neighboring qubits as seen in the conv_layer function below.

Note that we first apply the two qubit unitary to all even pairs of qubits followed by applying to odd pairs of qubits in a circular coupling manner, i.e. the as well as neighboring qubits being coupled, the first and final qubit are also coupled through a unitary gate.

Note that we add barriers into our quantum circuits for convenience when plotting, however they are not required for the actual QCNN and can be extracted from the following circuits.

def conv_layer(num_qubits, param_prefix):
    qc = QuantumCircuit(num_qubits, name="Convolutional Layer")
    qubits = list(range(num_qubits))
    param_index = 0
    params = ParameterVector(param_prefix, length=num_qubits * 3)
    for q1, q2 in zip(qubits[0::2], qubits[1::2]):
        qc = qc.compose(conv_circuit(params[param_index : (param_index + 3)]), [q1, q2])
        qc.barrier()
        param_index += 3
    for q1, q2 in zip(qubits[1::2], qubits[2::2] + [0]):
        qc = qc.compose(conv_circuit(params[param_index : (param_index + 3)]), [q1, q2])
        qc.barrier()
        param_index += 3

    qc_inst = qc.to_instruction()

    qc = QuantumCircuit(num_qubits)
    qc.append(qc_inst, qubits)
    return qc


circuit = conv_layer(4, "θ")
circuit.decompose().draw("mpl", style="clifford")

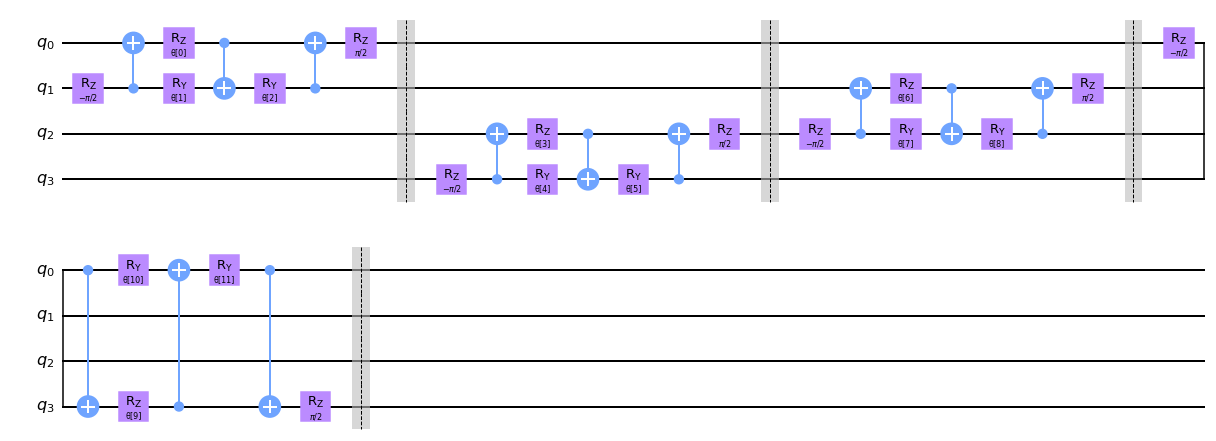
2.2 Pooling Layer

The purpose of a pooling layer is to reduce the dimensions of our Quantum Circuit, i.e. reduce the number of qubits in our circuit, while retaining as much information as possible from previously learned data. Reducing the amount of qubits also reduces the computational cost of the overall circuit, as the number of parameters that the QCNN needs to learn decreases.

However, one cannot simply decrease the amount of qubits in our quantum circuit. Because of this, we must define the pooling layer in a different manner compared with the classical approach.

To “artificially” reduce the number of qubits in our circuit, we first begin by creating pairs of the \(N\) qubits in our system.

After initially pairing all the qubits, we apply our generalized 2 qubit unitary to each pair, as described previously. After applying this two qubit unitary, we then ignore one qubit from each pair of qubits for the remainder of the neural network.

This layer therefore has the overall effect of “combining” the information of the two qubits into one qubit by first applying the unitary circuit, encoding information from one qubit into another, before disregarding one of qubits for the remainder of the circuit and not performing any operations or measurements on it.

We note that one could also apply a dynamic circuit to reduce the dimensionality in the pooling layers. This would involve performing measurements on certain qubits in the circuit and having an intermediate classical feedback loop in our pooling layers. By applying these measurements, one would also be reducing the dimensionality of the circuit.

In this tutorial, we apply the former approach, and disregard qubits in each pooling layer. Using this approach, we thus create a QCNN Pooling Layer which transforms the dimensions of our \(N\) qubit Quantum Circuit to \(N/2\).

To do so, we first define a two qubit unitary, which transforms the two qubit system to one.

def pool_circuit(params):
    target = QuantumCircuit(2)
    target.rz(-np.pi / 2, 1)
    target.cx(1, 0)
    target.rz(params[0], 0)
    target.ry(params[1], 1)
    target.cx(0, 1)
    target.ry(params[2], 1)

    return target


params = ParameterVector("θ", length=3)
circuit = pool_circuit(params)
circuit.draw("mpl", style="clifford")

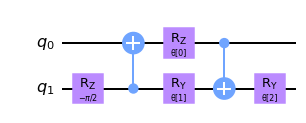
After applying this two qubit unitary circuit, we neglect the first qubit (q0) in future layers and only use the second qubit (q1) in our QCNN

We apply this two qubit pooling layer to different pairs of qubits to create our pooling layer for N qubits. As an example we then plot it for four qubits.

def pool_layer(sources, sinks, param_prefix):
    num_qubits = len(sources) + len(sinks)
    qc = QuantumCircuit(num_qubits, name="Pooling Layer")
    param_index = 0
    params = ParameterVector(param_prefix, length=num_qubits // 2 * 3)
    for source, sink in zip(sources, sinks):
        qc = qc.compose(pool_circuit(params[param_index : (param_index + 3)]), [source, sink])
        qc.barrier()
        param_index += 3

    qc_inst = qc.to_instruction()

    qc = QuantumCircuit(num_qubits)
    qc.append(qc_inst, range(num_qubits))
    return qc


sources = [0, 1]
sinks = [2, 3]
circuit = pool_layer(sources, sinks, "θ")
circuit.decompose().draw("mpl", style="clifford")

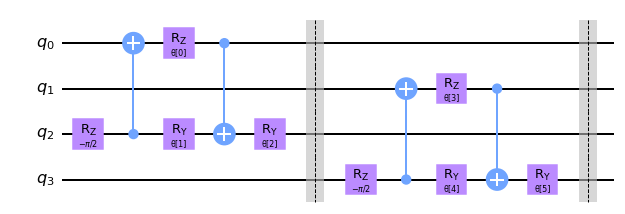
In this particular example, we reduce the dimensionality of our four qubit circuit to the last two qubits, i.e. the last two qubits in this particular example. These qubits are then used in the next layer, while the first two are neglected for the remainder of the QCNN.

3. Data Generation

One common use of a CCNN is an image classifier, where a CCNN detects particular features and patterns (such as straight lines or curves) of the pixelated images through the use of the feature maps in the convolutional layer. By learning the relationship between these features, it can then classify and label handwritten digits with ease.

Because of a classical CNN’s ability to recognize features and patterns easily, we will train our QCNN to also determine patterns and features of a given set of pixelated images, and classify between two different patterns.

To simplify the dataset, we only consider 2 x 4 pixelated images. The patterns we will train the QCNN to distinguish will be a horizontal or vertical line, which can be placed anywhere in the image, alongside a noisy background.

We first begin by generating this dataset. To create a “horizontal” or “vertical” line, we assign pixels value to be \(\frac{\pi}{2}\) which will represent the line in our pixelated image. We create a noisy background by assigning every other pixel a random value between \(0\) and \(\frac{\pi}{4}\) which will create a noisy background.

Note that when we create our dataset, we need to split it into the training set and testing set of images, the datasets we train and test our neural network respectively.

We also need to label our datasets such that the QCNN can learn to differentiate between the two patterns. In this example we label images with a horizontal line with -1 and images with a vertical line +1.

def generate_dataset(num_images):
    images = []
    labels = []
    hor_array = np.zeros((6, 8))
    ver_array = np.zeros((4, 8))

    j = 0
    for i in range(0, 7):
        if i != 3:
            hor_array[j][i] = np.pi / 2
            hor_array[j][i + 1] = np.pi / 2
            j += 1

    j = 0
    for i in range(0, 4):
        ver_array[j][i] = np.pi / 2
        ver_array[j][i + 4] = np.pi / 2
        j += 1

    for n in range(num_images):
        rng = algorithm_globals.random.integers(0, 2)
        if rng == 0:
            labels.append(-1)
            random_image = algorithm_globals.random.integers(0, 6)
            images.append(np.array(hor_array[random_image]))
        elif rng == 1:
            labels.append(1)
            random_image = algorithm_globals.random.integers(0, 4)
            images.append(np.array(ver_array[random_image]))

        # Create noise
        for i in range(8):
            if images[-1][i] == 0:
                images[-1][i] = algorithm_globals.random.uniform(0, np.pi / 4)
    return images, labels

Let’s now create our dataset below and split it into our test and training datasets. We pass a random_state so the split will be the same each time this notebook is run so the final results do not vary.

images, labels = generate_dataset(50)

train_images, test_images, train_labels, test_labels = train_test_split(
    images, labels, test_size=0.3, random_state=246
)

Let’s see some examples in our dataset

fig, ax = plt.subplots(2, 2, figsize=(10, 6), subplot_kw={"xticks": [], "yticks": []})
for i in range(4):
    ax[i // 2, i % 2].imshow(
        train_images[i].reshape(2, 4),  # Change back to 2 by 4
        aspect="equal",
    )
plt.subplots_adjust(wspace=0.1, hspace=0.025)

As we can see each image contains either a vertical or horizontal line, that the QCNN will learn how to differentiate. Now that we have built our dataset, it is time to discuss the components of the QCNN and build our model.

4. Modeling our QCNN

Now that we have defined both the convolutional layers it is now time to build our QCNN, which will consist of alternating pooling and convolutional layers.

As the images in our dataset contains 8 pixels, we will use 8 qubits in our QCNN.

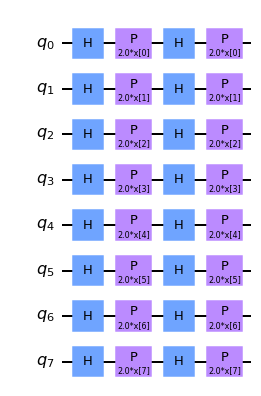
We encode our dataset into our QCNN by applying a feature map. One can create a feature map using one of Qiskit’s built in feature maps, such as ZFeatureMap or ZZFeatureMap.

After analyzing several different Feature maps for this dataset, it was found that QCNN obtains the greatest accuracy when the Z feature map is used. Therefore, throughout the remainder of the tutorial we will use the Z feature Map, of which can be seen below.

feature_map = ZFeatureMap(8)
feature_map.decompose().draw("mpl", style="clifford")

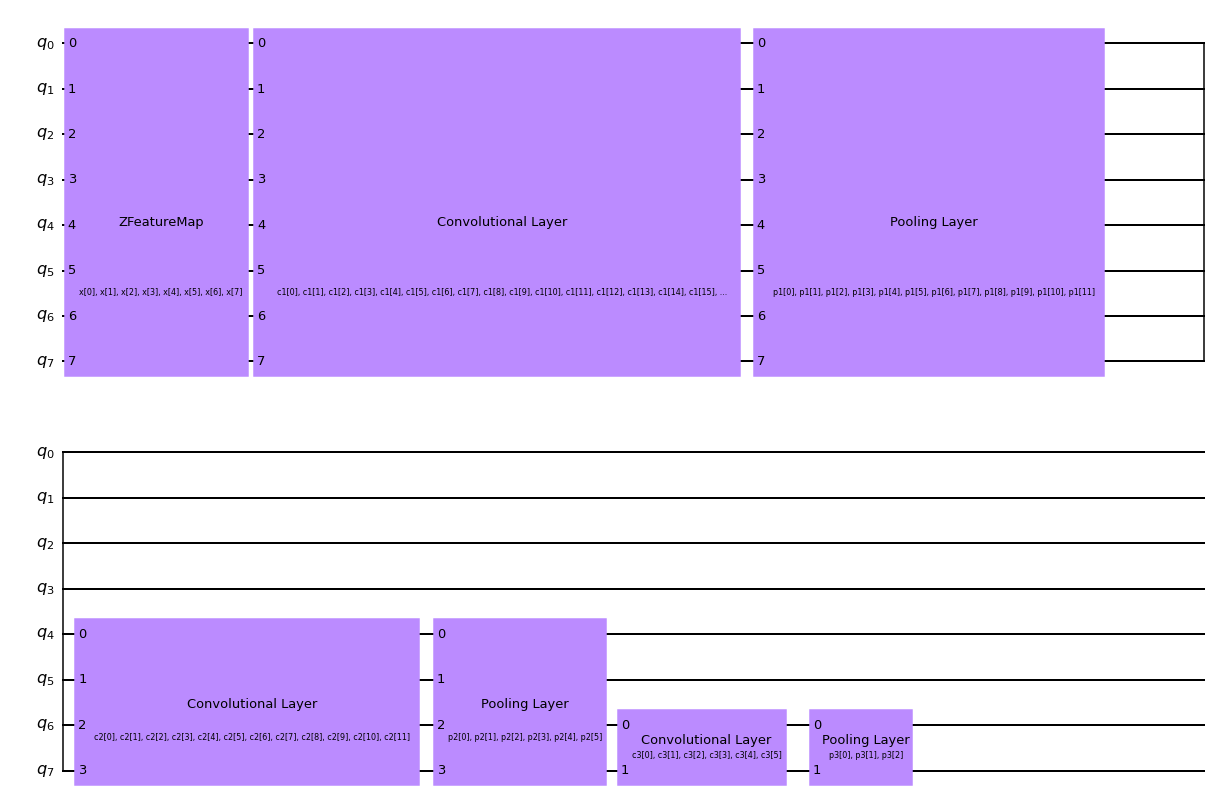
We create a function for our QCNN, which will contain three sets of alternating convolutional and pooling layers, which can be seen in the schematic below. Through the use of the pooling layers, we thus reduce the dimensionality of our QCNN from eight qubits to one.

To classify our image dataset of horizontal and vertical lines, we measure the expectation value of the Pauli Z operator of the final qubit. Based on the obtained value being +1 or -1, we can conclude that the input image contained either a horizontal or vertical line.

5. Training our QCNN

The next step is to build our model using our training data.

To classify our system, we perform a measurement from the output circuit. The value we obtain will thus classify whether our input data contains either a vertical line or horizontal line.

The measurement we have chosen in this tutorial is \(<Z>\), i.e. the expectation value of the Pauli Z qubit for the final qubit. Measuring this expectation value, we obtain +1 or -1, which correspond to a vertical or horizontal line respectively.

feature_map = ZFeatureMap(8)

ansatz = QuantumCircuit(8, name="Ansatz")

# First Convolutional Layer
ansatz.compose(conv_layer(8, "c1"), list(range(8)), inplace=True)

# First Pooling Layer
ansatz.compose(pool_layer([0, 1, 2, 3], [4, 5, 6, 7], "p1"), list(range(8)), inplace=True)

# Second Convolutional Layer
ansatz.compose(conv_layer(4, "c2"), list(range(4, 8)), inplace=True)

# Second Pooling Layer
ansatz.compose(pool_layer([0, 1], [2, 3], "p2"), list(range(4, 8)), inplace=True)

# Third Convolutional Layer
ansatz.compose(conv_layer(2, "c3"), list(range(6, 8)), inplace=True)

# Third Pooling Layer
ansatz.compose(pool_layer([0], [1], "p3"), list(range(6, 8)), inplace=True)

# Combining the feature map and ansatz
circuit = QuantumCircuit(8)
circuit.compose(feature_map, range(8), inplace=True)
circuit.compose(ansatz, range(8), inplace=True)

observable = SparsePauliOp.from_list([("Z" + "I" * 7, 1)])

# we decompose the circuit for the QNN to avoid additional data copying
qnn = EstimatorQNN(
    circuit=circuit.decompose(),
    observables=observable,
    input_params=feature_map.parameters,
    weight_params=ansatz.parameters,
)

circuit.draw("mpl", style="clifford")

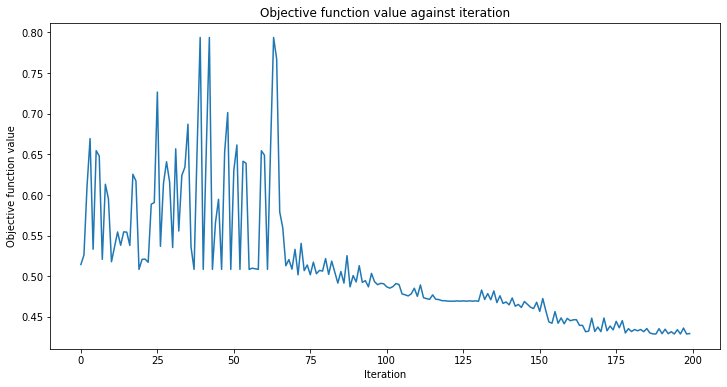
We will also define a callback function to use when training our model. This allows us to view and plot the loss function per each iteration in our training process.

def callback_graph(weights, obj_func_eval):
    clear_output(wait=True)
    objective_func_vals.append(obj_func_eval)
    plt.title("Objective function value against iteration")
    plt.xlabel("Iteration")
    plt.ylabel("Objective function value")
    plt.plot(range(len(objective_func_vals)), objective_func_vals)
    plt.show()

In this example, we will use the COBYLA optimizer to train our classifier, which is a numerical optimization method commonly used for classification machine learning algorithms.

We then place the the callback function, optimizer and operator of our QCNN created above into Qiskit Machine Learning’s built in Neural Network Classifier, which we can then use to train our model.

Since model training may take a long time we have already pre-trained the model for some iterations and saved the pre-trained weights. We’ll continue training from that point by setting initial_point to a vector of pre-trained weights.

with open("11_qcnn_initial_point.json", "r") as f:
    initial_point = json.load(f)

classifier = NeuralNetworkClassifier(
    qnn,
    optimizer=COBYLA(maxiter=200),  # Set max iterations here
    callback=callback_graph,
    initial_point=initial_point,
)

After creating this classifier, we can train our QCNN using our training dataset and each image’s corresponding label. Because we previously defined the callback function, we plot the overall loss of our system per iteration.

It may take some time to train the QCNN so be patient!

x = np.asarray(train_images)
y = np.asarray(train_labels)

objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
classifier.fit(x, y)

# score classifier
print(f"Accuracy from the train data : {np.round(100 * classifier.score(x, y), 2)}%")

Accuracy from the train data : 97.14%

As we can see from above, the QCNN converges slowly, hence our initial_point was already close to an optimal solution. The next step is to determine whether our QCNN can classify data seen in our test image data set.

6. Testing our QCNN

After building and training our dataset we now test whether our QCNN can predict images that are not from our test data set.

y_predict = classifier.predict(test_images)
x = np.asarray(test_images)
y = np.asarray(test_labels)
print(f"Accuracy from the test data : {np.round(100 * classifier.score(x, y), 2)}%")

# Let's see some examples in our dataset
fig, ax = plt.subplots(2, 2, figsize=(10, 6), subplot_kw={"xticks": [], "yticks": []})
for i in range(0, 4):
    ax[i // 2, i % 2].imshow(test_images[i].reshape(2, 4), aspect="equal")
    if y_predict[i] == -1:
        ax[i // 2, i % 2].set_title("The QCNN predicts this is a Horizontal Line")
    if y_predict[i] == +1:
        ax[i // 2, i % 2].set_title("The QCNN predicts this is a Vertical Line")
plt.subplots_adjust(wspace=0.1, hspace=0.5)

Accuracy from the test data : 93.33%

From above, we can indeed see that our QCNN can classify horizontal and vertical lines! Congratulations! Through the use of quantum circuits and quantum convolutional and pooling layers, you have built a Quantum Convolutional Neural Network!

7. References

[1] Cong, I., Choi, S. & Lukin, M.D. Quantum convolutional neural networks. Nat. Phys. 15, 1273–1278 (2019). https://doi.org/10.1038/s41567-019-0648-8

[2] IBM Convolutional Neural Networks https://www.ibm.com/cloud/learn/convolutional-neural-networks

[3] Vatan, Farrokh, and Colin Williams. « Optimal quantum circuits for general two-qubit gates. » Physical Review A 69.3 (2004): 032315.

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Software	Version
qiskit	1.0.0.dev0+737f21b
qiskit_algorithms	0.3.0
qiskit_machine_learning	0.8.0
System information
Python version	3.9.7
Python compiler	GCC 7.5.0
Python build	default, Sep 16 2021 13:09:58
OS	Linux
CPUs	2
Memory (Gb)	5.792198181152344
Thu Dec 14 13:53:25 2023 EST

This code is a part of Qiskit

© Copyright IBM 2017, 2023.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.