Note
Cette page a été générée à partir de ` docs/tutorials/07_pegasos_qsvc.ipynb ` __.
Classificateur de vecteur de support quantique Pegasos Quantum#
Il y a un autre algorithme basé sur SVM qui bénéficie de la méthode du noyau quantique. Ici, nous introduisons une implémentation d’un autre algorithme de classification, qui est une version alternative au ` ` QSVC ` ` disponible dans Qiskit Machine Learning et montré dans le tutoriel « Quantum Kernel Machine Learning » <./03_quantum_kernel.ipynb> ` __ tutorial. Cet algorithme de classification implémente l’algorithme de Pegasos à partir de l’article « Pegasos: Primal Estimated sub-GrAdient SOlver for SVM » de Shalev-Shwartz et al., voir: https://home.ttic.edu/ ~ nati/Publications/PegasosMPB.pdf.
Cet algorithme est une alternative à la double optimisation du paquet scikit-learn, bénéficie de l’astuce du noyau et donne une complexité de formation qui est indépendante de la taille de l’ensemble de formation. Ainsi, le PegasosQSVC devrait s’entraîner plus rapidement que le QSVC pour des formations suffisamment grandes.
L’algorithme peut être utilisé comme remplacement direct de QSVC avec une hyper-paramétrisation.
Nous allons générer quelques données :
[1]:
from sklearn.datasets import make_blobs
# example dataset
features, labels = make_blobs(n_samples=20, n_features=2, centers=2, random_state=3, shuffle=True)
Nous pré-traitons les données pour assurer la compatibilité avec l’encodage de rotation et le divisons en jeux de données de formation et de test.
[2]:
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
features = MinMaxScaler(feature_range=(0, np.pi)).fit_transform(features)
train_features, test_features, train_labels, test_labels = train_test_split(
features, labels, train_size=15, shuffle=False
)
Nous avons deux fonctionnalités dans le jeu de données, donc nous avons défini un certain nombre de qubits sur le nombre de fonctionnalités dans le jeu de données.
Ensuite, nous avons fixé \(\tau\) au nombre d’étapes effectuées au cours de la procédure de formation. Veuillez noter qu’il n’y a pas de critère d’arrêt anticipé dans l’algorithme. L’algorithme itère sur toutes les étapes \(\tau\).
Et le dernier est le paramètre hyperparamètre \(C\). Il s’agit d’un paramètre de régularisation positif. La force de la régularisation est inversement proportionnelle à \(C\). Smaller \(C\) induise des poids plus petits qui aident généralement à prévenir le surajustement. Cependant, en raison de la nature de cet algorithme, certaines des étapes de calcul deviennent triviales pour les plus gros \(C\). Ainsi, les plus grands \(C\) améliorent considérablement la performance de l’algorithme. Si les données sont séparables linéairement dans l’espace de fonctions, :math:`C`doit être choisi comme étant grand. Si la séparation n’est pas parfaite, le :math:`C`doit être choisi plus petit pour éviter le surajustement.
[3]:
# number of qubits is equal to the number of features
num_qubits = 2
# number of steps performed during the training procedure
tau = 100
# regularization parameter
C = 1000
L’algorithme s’exécutera à l’aide de :
The default fidelity instantiated in
FidelityQuantumKernelA quantum kernel created from
ZFeatureMap
[4]:
from qiskit import BasicAer
from qiskit.circuit.library import ZFeatureMap
from qiskit_algorithms.utils import algorithm_globals
from qiskit_machine_learning.kernels import FidelityQuantumKernel
algorithm_globals.random_seed = 12345
feature_map = ZFeatureMap(feature_dimension=num_qubits, reps=1)
qkernel = FidelityQuantumKernel(feature_map=feature_map)
The implementation PegasosQSVC is compatible with the scikit-learn interfaces and has a pretty standard way of training a model. In the constructor we pass parameters of the algorithm, in this case there are a regularization hyper-parameter \(C\) and a number of steps.
Then we pass training features and labels to the fit method, which trains a models and returns a fitted classifier.
Afterwards, we score our model using test features and labels.
[5]:
from qiskit_machine_learning.algorithms import PegasosQSVC
pegasos_qsvc = PegasosQSVC(quantum_kernel=qkernel, C=C, num_steps=tau)
# training
pegasos_qsvc.fit(train_features, train_labels)
# testing
pegasos_score = pegasos_qsvc.score(test_features, test_labels)
print(f"PegasosQSVC classification test score: {pegasos_score}")
PegasosQSVC classification test score: 1.0
For visualization purposes we create a mesh grid of a predefined step that spans our minimum and maximum values we applied in MinMaxScaler. We also add some margin to the grid for better representation of the training and test samples.
[6]:
grid_step = 0.2
margin = 0.2
grid_x, grid_y = np.meshgrid(
np.arange(-margin, np.pi + margin, grid_step), np.arange(-margin, np.pi + margin, grid_step)
)
We convert the grid to the shape compatible with the model, the shape should be (n_samples, n_features). Then for each grid point we predict a label. In our case predicted labels will be used for coloring the grid.
[7]:
meshgrid_features = np.column_stack((grid_x.ravel(), grid_y.ravel()))
meshgrid_colors = pegasos_qsvc.predict(meshgrid_features)
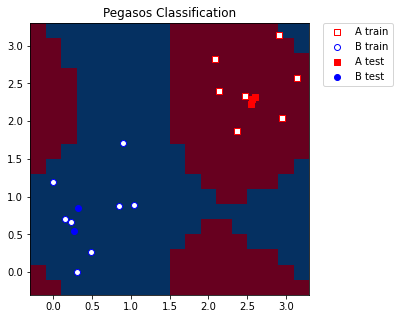
Finally, we plot our grid according to the labels/colors we obtained from the model. We also plot training and test samples.
[8]:
import matplotlib.pyplot as plt
plt.figure(figsize=(5, 5))
meshgrid_colors = meshgrid_colors.reshape(grid_x.shape)
plt.pcolormesh(grid_x, grid_y, meshgrid_colors, cmap="RdBu", shading="auto")
plt.scatter(
train_features[:, 0][train_labels == 0],
train_features[:, 1][train_labels == 0],
marker="s",
facecolors="w",
edgecolors="r",
label="A train",
)
plt.scatter(
train_features[:, 0][train_labels == 1],
train_features[:, 1][train_labels == 1],
marker="o",
facecolors="w",
edgecolors="b",
label="B train",
)
plt.scatter(
test_features[:, 0][test_labels == 0],
test_features[:, 1][test_labels == 0],
marker="s",
facecolors="r",
edgecolors="r",
label="A test",
)
plt.scatter(
test_features[:, 0][test_labels == 1],
test_features[:, 1][test_labels == 1],
marker="o",
facecolors="b",
edgecolors="b",
label="B test",
)
plt.legend(bbox_to_anchor=(1.05, 1), loc="upper left", borderaxespad=0.0)
plt.title("Pegasos Classification")
plt.show()
[9]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.22.0 |
qiskit-aer | 0.11.0 |
qiskit-ignis | 0.7.0 |
qiskit | 0.33.0 |
qiskit-machine-learning | 0.5.0 |
| System information | |
| Python version | 3.7.9 |
| Python compiler | MSC v.1916 64 bit (AMD64) |
| Python build | default, Aug 31 2020 17:10:11 |
| OS | Windows |
| CPUs | 4 |
| Memory (Gb) | 31.837730407714844 |
| Thu Oct 13 10:42:49 2022 GMT Daylight Time | |
This code is a part of Qiskit
© Copyright IBM 2017, 2022.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.