注釈
このページは docs/tutorials/01_neural_networks.ipynb から生成されました。
量子ニューラル・ネットワーク#
概要#
このノートブックでは、 qiskit-machine-learning で提供されるさまざまな量子ニューラルネットワーク (QNN) の実装と、それらを基本的な量子機械学習 (QML) ワークフローに統合する方法について説明します。
このチュートリアルの構造は以下のとおりです。
はじめに
QNNをインスタンス化する方法
フォワード・パスの実行方法
バックワード・パスの実行方法
拡張機能
結論
1. はじめに#
1.1. 量子対古典的ニューラルネットワーク#
古典的なニューラルネットワークは、人間の脳に触発されたアルゴリズム・モデルで、データのパターンを認識し、複雑な問題の解決を学習できます。 一連の相互接続されたノード (ニューロン) が基礎となり、層構造で構成され、機械学習や深層学習の戦略を適用することで学習できるパラメーターから成ります。
量子機械学習 (QML) の背後にある動機は、量子コンピューティングと古典的機械学習からの概念を統合し、新しくかつ改良された学習スキームの方法を開くことです。QNN は、古典的なニューラルネットワークとパラメーター化された量子回路を結合することにより、この一般的な原理を適用します。2 つの分野間の交差点に位置するため、 QNN は次の 2 つの観点から見ることができます。
機械学習の観点 から言うと、 QNN は、改めて、古典的なものと同様にデータの隠れたパターンを見つけるために訓練できるアルゴリズム・モデルです。 これらのモデルは、古典データ (入力) を量子状態に 読み込む ことができ、訓練可能な重み によりパラメーター化された量子ゲートとともに 処理 されます。 図1は、データの読み込みおよび処理のステップを含む、汎用 QNN の例を示しています。 この状態を測定した出力を損失関数に差し込んで、誤差逆伝播法を通して重みを訓練することができます。
量子コンピューティングの観点 から言うと、QNNはパラメーター化された量子回路に基づいた量子アルゴリズムで、古典的なオプティマイザーを使用して変分法で訓練することができます。 これらの回路には、図1に示すように フィーチャーマップ (入力パラメーター付き) と ansatz (訓練可能な重み付き) が含まれています。
図1. 一般的な量子ニューラルネットワーク(QNN) の構造
ご覧の通り、これらの 2 つの視点は補完なものであり、必ずしも「量子ニューロン」や QNNの「層」といった概念の厳密な定義に依存するわけではありません。
1.2. qiskit-machine-learning での実装#
qiskit-machine-learning の QNN は、さまざまなユースケースで使用できるアプリケーションに依存しない計算ユニットとして使用されます。 それらの設定は必要なアプリケーションによって異なります このモジュールには、QNNのインターフェースと 2 つの特定の実装が含まれています。
NeuralNetwork: ニューラルネットワークのインターフェイス。これは全ての QNN が継承する抽象クラスです。
EstimatorQNN: 量子力学的観測可能量の評価に基づくネットワーク。
SamplerQNN: 量子回路の測定から得られたサンプルを基にしたネットワーク。
これらの実装は qiskit primitive に基づいています。 primitiveは、シミュレーターまたは実際の量子ハードウェア上で QNN を実行するエントリー・ポイントです。 それぞれの実装である EstimatorQNN と SamplerQNN は、対応するprimitive (BaseEstimator と BaseSampler の任意のサブクラス) のオプション・インスタンスを取り込みます。
qiskit.primitives モジュールは、状態ベクトル・シミュレーションを実行するための Sampler と Estimator クラスの参照実装を提供します。 デフォルトでは、QNNクラスにインスタンスが渡されていない場合、対応する参照primitiveのインスタンス (Sampler または Estimator) は、ネットワークによって自動的に作成されます。 primitiveについての詳細は、 primitiveドキュメント を参照してください。
NeuralNetwork クラスは、qiskit-machine-learning で利用可能なすべての QNN のインターフェイスです。 これは、データ・サンプルと訓練可能な重みを入力として取るフォワードおよびバックワード・パスを公開します。
NeuralNetwork は「ステートレス」であることに注意する必要があります。学習能力を有さず (学習能力は実際のアルゴリズムやアプリケーションに任されます: 分類器, 回帰器, など) 、訓練可能ウェイトの値を保持しません。
では、2 つの NeuralNetwork 実装の具体的な例を見てみましょう。 しかし、まず、実行間で結果が変わらないようにアルゴリズムのシードを設定しましょう。
[25]:
from qiskit_algorithms.utils import algorithm_globals
algorithm_globals.random_seed = 42
2. QNNをインスタンス化する方法#
2.1. EstimatorQNN#
EstimatorQNN は、オプションの量子力学的観測可能量と同様に、パラメーター化された量子回路を入力として取り込み、フォワード・パスの期待値計算を出力します。 EstimatorQNN は、より複雑な QNN を構築するために観測量のリストも受け入れます。
簡単な例を使って、 EstimatorQNN の動きを見てみましょう。パラメーター化回路の構築から始めます。この量子回路には2つのパラメータがあります。1つはQNNの入力を表し、もう1つは訓練可能な重みを表します。
[26]:
from qiskit.circuit import Parameter
from qiskit import QuantumCircuit
params1 = [Parameter("input1"), Parameter("weight1")]
qc1 = QuantumCircuit(1)
qc1.h(0)
qc1.ry(params1[0], 0)
qc1.rx(params1[1], 0)
qc1.draw("mpl")
[26]:
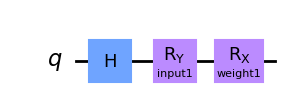
これで、期待値計算を定義するための観測量を作成できるようになりました。 設定していない場合、 EstimatorQNN は自動的にデフォルトの観測量 \(Z^{\otimes n}\) :math:を作成します。 ここで、\(n\) は量子回路の量子ビット数です。
この例では、一転して \(Y^{\otimes n}\) 観測量を使用します。
[27]:
from qiskit.quantum_info import SparsePauliOp
observable1 = SparsePauliOp.from_list([("Y" * qc1.num_qubits, 1)])
上記で定義された量子回路と作成した観測量と共に、 EstimatorQNN のコンストラクタは次のキーワード引数を取ります。
estimator: オプションのprimitiveインスタンスinput_params: 「ネットワーク入力」として扱うべき量子回路パラメーターのリストweight_params:「ネットワークの重み」として扱われるべき量子回路パラメーターのリスト
この例では、params1 の最初のパラメーターを入力とし、2番目のパラメーターを重みとしました。 ローカルの状態ベクトル・シミュレーションを実行しているので、estimator パラメーターを設定しません。ネットワークは、参照 Estimator primitiveのインスタンスを作成します。 クラウド・リソースや Aer シミュレーターにアクセスする必要がある場合は、それぞれの Estimator インスタンスを定義し、それらを EstimatorQNN に渡す必要があります。
[28]:
from qiskit_machine_learning.neural_networks import EstimatorQNN
estimator_qnn = EstimatorQNN(
circuit=qc1, observables=observable1, input_params=[params1[0]], weight_params=[params1[1]]
)
estimator_qnn
[28]:
<qiskit_machine_learning.neural_networks.estimator_qnn.EstimatorQNN at 0x7fd668ca0e80>
次のセクションでQNNの使い方を見ていきますが、その前に SamplerQNN クラスを見てみましょう。
2.2. SamplerQNN#
SamplerQNN は、EstimatorQNN と同様にインスタンス化されます。 しかし、量子回路の測定から直接サンプルを吸収するので、カスタム観測量を必要としません。
これらの出力サンプルは、デフォルトでは、ビット文字列に対応する整数インデックスを測定する確率として解釈されます。 しかし、SamplerQNN ではサンプルを後処理するための interpret 関数を指定することもできます。 この関数は (ビット文字列から) 測定された整数を取って、それを新しい値、すなわち非負の整数にマップするように定義する必要があります。
(!) カスタムの interpret 関数が定義されている場合、 output_shape はネットワークでは推論できないので、 明示的に提供する必要がある ことに注意してください。
(!) interpret 関数を使用しない場合、確率ベクトルの次元は量子ビット数に応じて指数関数的に増加することにも注意してください。 カスタム interpret 関数を使用する場合、この増加を変更できます。例えば、インデックスが対応するビット文字列のパリティにマッピングされる場合、つまり0または1にマッピングされる場合、結果は量子ビット数に関係なく長さ2の確率ベクトルになります。
SamplerQNN 用に別の量子回路を作成しましょう。 この場合、2 つの入力パラメーターと 4 つの訓練可能な重みを持ち、Two-local 回路をパラメーター化します。
[29]:
from qiskit.circuit import ParameterVector
inputs2 = ParameterVector("input", 2)
weights2 = ParameterVector("weight", 4)
print(f"input parameters: {[str(item) for item in inputs2.params]}")
print(f"weight parameters: {[str(item) for item in weights2.params]}")
qc2 = QuantumCircuit(2)
qc2.ry(inputs2[0], 0)
qc2.ry(inputs2[1], 1)
qc2.cx(0, 1)
qc2.ry(weights2[0], 0)
qc2.ry(weights2[1], 1)
qc2.cx(0, 1)
qc2.ry(weights2[2], 0)
qc2.ry(weights2[3], 1)
qc2.draw(output="mpl")
input parameters: ['input[0]', 'input[1]']
weight parameters: ['weight[0]', 'weight[1]', 'weight[2]', 'weight[3]']
[29]:
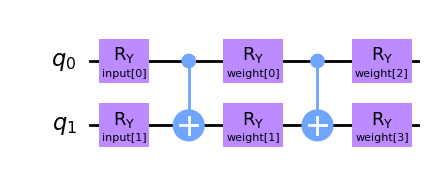
EstimatorQNN と同様に、SamplerQNN をインスタンス化する際に入力と重みを指定する必要があります。 この場合、キーワード引数は以下のようになります: - sampler: オプションのprimitiveインスタンス - input_params: 「ネットワーク入力」として扱われるべき量子回路パラメーターのリスト - weight_params: 「ネットワーク重み」として扱われるべき量子回路パラメーターのリスト
再び、Sampler インスタンスを QNN に設定しないことを選択し、デフォルトに依存していることに注意してください。
[30]:
from qiskit_machine_learning.neural_networks import SamplerQNN
sampler_qnn = SamplerQNN(circuit=qc2, input_params=inputs2, weight_params=weights2)
sampler_qnn
[30]:
<qiskit_machine_learning.neural_networks.sampler_qnn.SamplerQNN at 0x7fd659264880>
上記の基本的な引数に加えて、SamplerQNN は input_gradients と interpret と output_shape の 3 つの設定を受け付けます。 これらはセクション4とセクション5で紹介されます。
3. フォワード・パスの実行方法#
3.1. セットアップ#
実際の設定では、入力はデータセットによって定義され、重みは学習アルゴリズムや学習済みモデルの一部として定義されます。しかし、このチュートリアルのために、適切な次元の入力と重みのランダムなセットを指定します。
3.1.1. EstimatorQNN の例#
[31]:
estimator_qnn_input = algorithm_globals.random.random(estimator_qnn.num_inputs)
estimator_qnn_weights = algorithm_globals.random.random(estimator_qnn.num_weights)
[32]:
print(
f"Number of input features for EstimatorQNN: {estimator_qnn.num_inputs} \nInput: {estimator_qnn_input}"
)
print(
f"Number of trainable weights for EstimatorQNN: {estimator_qnn.num_weights} \nWeights: {estimator_qnn_weights}"
)
Number of input features for EstimatorQNN: 1
Input: [0.77395605]
Number of trainable weights for EstimatorQNN: 1
Weights: [0.43887844]
3.1.2. SamplerQNN の例#
[33]:
sampler_qnn_input = algorithm_globals.random.random(sampler_qnn.num_inputs)
sampler_qnn_weights = algorithm_globals.random.random(sampler_qnn.num_weights)
[34]:
print(
f"Number of input features for SamplerQNN: {sampler_qnn.num_inputs} \nInput: {sampler_qnn_input}"
)
print(
f"Number of trainable weights for SamplerQNN: {sampler_qnn.num_weights} \nWeights: {sampler_qnn_weights}"
)
Number of input features for SamplerQNN: 2
Input: [0.85859792 0.69736803]
Number of trainable weights for SamplerQNN: 4
Weights: [0.09417735 0.97562235 0.7611397 0.78606431]
入力と重みを設定したら、バッチパスと非バッチパスの結果を確認しましょう。
3.2. 非バッチ・フォワード・パス#
3.2.1. EstimatorQNN の例#
EstimatorQNN では、フォワード・パスの期待される出力形状は (1, num_qubits * num_observables) です。ここで 1 はサンプル数です:
[35]:
estimator_qnn_forward = estimator_qnn.forward(estimator_qnn_input, estimator_qnn_weights)
print(
f"Forward pass result for EstimatorQNN: {estimator_qnn_forward}. \nShape: {estimator_qnn_forward.shape}"
)
Forward pass result for EstimatorQNN: [[0.2970094]].
Shape: (1, 1)
3.2.2. SamplerQNN の例#
SamplerQNN (カスタム interpret 関数なし) では、フォワード・パスの期待される出力形状は (1, 2**num_qubits) になります。 カスタム interpret 関数を使用すると、出力形状は (1, output_shape) になります。ここで、1 はサンプル数です。
[36]:
sampler_qnn_forward = sampler_qnn.forward(sampler_qnn_input, sampler_qnn_weights)
print(
f"Forward pass result for SamplerQNN: {sampler_qnn_forward}. \nShape: {sampler_qnn_forward.shape}"
)
Forward pass result for SamplerQNN: [[0.01826527 0.25735654 0.5267981 0.19758009]].
Shape: (1, 4)
3.3. バッチ・フォワード・パス#
3.3.1. EstimatorQNN の例#
EstimatorQNN では、フォワード・パスの期待される出力形状は``(batch_size, num_qubits * num_observables)`` になります。
[37]:
estimator_qnn_forward_batched = estimator_qnn.forward(
[estimator_qnn_input, estimator_qnn_input], estimator_qnn_weights
)
print(
f"Forward pass result for EstimatorQNN: {estimator_qnn_forward_batched}. \nShape: {estimator_qnn_forward_batched.shape}"
)
Forward pass result for EstimatorQNN: [[0.2970094]
[0.2970094]].
Shape: (2, 1)
3.3.2. SamplerQNN の例#
SamplerQNN (カスタム interpret 関数なし) では、フォワード・パスの期待される出力形状は (batch_size, 2**num_qubits) になります。 カスタム interpret 関数を使用すると、出力形状は (batch_size, output_shape) になります。
[38]:
sampler_qnn_forward_batched = sampler_qnn.forward(
[sampler_qnn_input, sampler_qnn_input], sampler_qnn_weights
)
print(
f"Forward pass result for SamplerQNN: {sampler_qnn_forward_batched}. \nShape: {sampler_qnn_forward_batched.shape}"
)
Forward pass result for SamplerQNN: [[0.01826527 0.25735654 0.5267981 0.19758009]
[0.01826527 0.25735654 0.5267981 0.19758009]].
Shape: (2, 4)
4. バックワード・パスの実行方法#
上記で定義した入力と重みを利用して、バックワード・パスの動作を示しましょう。このパスはタプル (input_gradients, weight_gradients) を返します。 デフォルトでは、バックワード・パスは重みパラメーターに対する勾配のみを計算します。
入力パラメーターに対して勾配を有効にする場合は、QNN インスタンスを作成するときに次のフラグを設定する必要があります。
qnn = ...QNN(..., input_gradients=True)
PyTorchとの統合に TorchConnector を使用するには、入力勾配が 必要 であることを忘れないでください。
4.1. 入力勾配のないバックワード・パス#
4.1.1. EstimatorQNN の例#
EstimatorQNN では、重み勾配の期待される出力形状は (batch_size, num_qubits * num_observables, num_weights) になります。
[39]:
estimator_qnn_input_grad, estimator_qnn_weight_grad = estimator_qnn.backward(
estimator_qnn_input, estimator_qnn_weights
)
print(
f"Input gradients for EstimatorQNN: {estimator_qnn_input_grad}. \nShape: {estimator_qnn_input_grad}"
)
print(
f"Weight gradients for EstimatorQNN: {estimator_qnn_weight_grad}. \nShape: {estimator_qnn_weight_grad.shape}"
)
Input gradients for EstimatorQNN: None.
Shape: None
Weight gradients for EstimatorQNN: [[[0.63272767]]].
Shape: (1, 1, 1)
4.1.2. SamplerQNN の例#
SamplerQNN (カスタム interpret 関数なし) では、フォワード・パスの期待される出力形状は (batch_size, 2**num_qubits, num_weights) になります。 カスタム interpret 関数を使用すると、出力形状は (batch_size, output_shape, num_weights) になります。
[40]:
sampler_qnn_input_grad, sampler_qnn_weight_grad = sampler_qnn.backward(
sampler_qnn_input, sampler_qnn_weights
)
print(
f"Input gradients for SamplerQNN: {sampler_qnn_input_grad}. \nShape: {sampler_qnn_input_grad}"
)
print(
f"Weight gradients for SamplerQNN: {sampler_qnn_weight_grad}. \nShape: {sampler_qnn_weight_grad.shape}"
)
Input gradients for SamplerQNN: None.
Shape: None
Weight gradients for SamplerQNN: [[[ 0.00606238 -0.1124595 -0.06856156 -0.09809236]
[ 0.21167414 -0.09069775 0.06856156 -0.22549618]
[-0.48846674 0.32499215 -0.32262178 0.09809236]
[ 0.27073021 -0.12183491 0.32262178 0.22549618]]].
Shape: (1, 4, 4)
4.2. 入力勾配のあるバックワード・パス#
input_gradients を有効にして、このオプションで期待される出力サイズを表示しましょう。
[41]:
estimator_qnn.input_gradients = True
sampler_qnn.input_gradients = True
4.2.1. EstimatorQNN の例#
EstimatorQNN では、重み勾配の期待される出力形状は (batch_size, num_qubits * num_observables, num_inputs) になります。
[42]:
estimator_qnn_input_grad, estimator_qnn_weight_grad = estimator_qnn.backward(
estimator_qnn_input, estimator_qnn_weights
)
print(
f"Input gradients for EstimatorQNN: {estimator_qnn_input_grad}. \nShape: {estimator_qnn_input_grad.shape}"
)
print(
f"Weight gradients for EstimatorQNN: {estimator_qnn_weight_grad}. \nShape: {estimator_qnn_weight_grad.shape}"
)
Input gradients for EstimatorQNN: [[[0.3038852]]].
Shape: (1, 1, 1)
Weight gradients for EstimatorQNN: [[[0.63272767]]].
Shape: (1, 1, 1)
4.2.2. SamplerQNN の例#
SamplerQNN (カスタム interpret 関数なし) では、入力勾配に対する期待される出力形状は (batch_size, 2**num_qubits, num_inputs) になります。 カスタム interpret 関数を使用すると、出力形状は (batch_size, output_shape, num_inputs) になります。
[43]:
sampler_qnn_input_grad, sampler_qnn_weight_grad = sampler_qnn.backward(
sampler_qnn_input, sampler_qnn_weights
)
print(
f"Input gradients for SamplerQNN: {sampler_qnn_input_grad}. \nShape: {sampler_qnn_input_grad.shape}"
)
print(
f"Weight gradients for SamplerQNN: {sampler_qnn_weight_grad}. \nShape: {sampler_qnn_weight_grad.shape}"
)
Input gradients for SamplerQNN: [[[-0.05844702 -0.10621091]
[ 0.38798796 -0.19544083]
[-0.34561132 0.09459601]
[ 0.01607038 0.20705573]]].
Shape: (1, 4, 2)
Weight gradients for SamplerQNN: [[[ 0.00606238 -0.1124595 -0.06856156 -0.09809236]
[ 0.21167414 -0.09069775 0.06856156 -0.22549618]
[-0.48846674 0.32499215 -0.32262178 0.09809236]
[ 0.27073021 -0.12183491 0.32262178 0.22549618]]].
Shape: (1, 4, 4)
5. 拡張機能#
5.1. 複数の観測量を持つ EstimatorQNN#
EstimatorQNN では、より複雑な QNN アーキテクチャーのために観測量のリストを渡すことができます。例えば (出力形状の変化に注意してください)
[44]:
observable2 = SparsePauliOp.from_list([("Z" * qc1.num_qubits, 1)])
estimator_qnn2 = EstimatorQNN(
circuit=qc1,
observables=[observable1, observable2],
input_params=[params1[0]],
weight_params=[params1[1]],
)
[45]:
estimator_qnn_forward2 = estimator_qnn2.forward(estimator_qnn_input, estimator_qnn_weights)
estimator_qnn_input_grad2, estimator_qnn_weight_grad2 = estimator_qnn2.backward(
estimator_qnn_input, estimator_qnn_weights
)
print(f"Forward output for EstimatorQNN1: {estimator_qnn_forward.shape}")
print(f"Forward output for EstimatorQNN2: {estimator_qnn_forward2.shape}")
print(f"Backward output for EstimatorQNN1: {estimator_qnn_weight_grad.shape}")
print(f"Backward output for EstimatorQNN2: {estimator_qnn_weight_grad2.shape}")
Forward output for EstimatorQNN1: (1, 1)
Forward output for EstimatorQNN2: (1, 2)
Backward output for EstimatorQNN1: (1, 1, 1)
Backward output for EstimatorQNN2: (1, 2, 1)
5.2. カスタム interpret 付き SamplerQNN#
SamplerQNN の一般的な interpret メソッドの 1 つは parity 関数で、バイナリ分類を行うことができます。 インスタンス作成のセクションで説明したように、interpret 関数を使うことで、フォワードとバックワード・パスの出力形状が変更されます。 パリティinterpret関数の場合、output_shape は 2 に固定されます。 そこで期待される前方および重み勾配の形状は、おそれぞれ (batch_size, 2) と (batch_size, 2, num_weights) です。
[46]:
parity = lambda x: "{:b}".format(x).count("1") % 2
output_shape = 2 # parity = 0, 1
sampler_qnn2 = SamplerQNN(
circuit=qc2,
input_params=inputs2,
weight_params=weights2,
interpret=parity,
output_shape=output_shape,
)
[47]:
sampler_qnn_forward2 = sampler_qnn2.forward(sampler_qnn_input, sampler_qnn_weights)
sampler_qnn_input_grad2, sampler_qnn_weight_grad2 = sampler_qnn2.backward(
sampler_qnn_input, sampler_qnn_weights
)
print(f"Forward output for SamplerQNN1: {sampler_qnn_forward.shape}")
print(f"Forward output for SamplerQNN2: {sampler_qnn_forward2.shape}")
print(f"Backward output for SamplerQNN1: {sampler_qnn_weight_grad.shape}")
print(f"Backward output for SamplerQNN2: {sampler_qnn_weight_grad2.shape}")
Forward output for SamplerQNN1: (1, 4)
Forward output for SamplerQNN2: (1, 2)
Backward output for SamplerQNN1: (1, 4, 4)
Backward output for SamplerQNN2: (1, 2, 4)
6. 結論#
このチュートリアルでは、qiskit-machine-learning によって提供される2つのニューラルネットワーク・クラス、つまり EstimatorQNN と SamplerQNN について紹介しました。 QNN初期化のための重要なステップ、フォワードおよびバックワード・パスでの基本的な使用法、および高度な機能のいくつかの理論的背景を提供しました。
この問題設定を扱って、さまざまな回路のサイズ、入力、重みパラメーターの長さが、出力形状にどのように影響を与えるか確認することをお勧めします。
[48]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.22.3 |
qiskit-machine-learning | 0.6.0 |
| System information | |
| Python version | 3.9.15 |
| Python compiler | Clang 14.0.6 |
| Python build | main, Nov 24 2022 08:29:02 |
| OS | Darwin |
| CPUs | 8 |
| Memory (Gb) | 64.0 |
| Mon Jan 23 11:57:49 2023 CET | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.