注釈
このページは docs/tutorials/12_quantum_autoencoder.ipynb から生成されました。
量子オートエンコーダー#
このチュートリアルの目的は、量子オートエンコーダを作ることです。量子オートエンコーダーは、初期状態からの情報を保持しながら、より少ない量子ビットに量子状態を圧縮できる回路です。
このチュートリアルでは、量子オートエンコーダーのアーキテクチャーと、情報を圧縮し符号化するためにどのように設計し訓練できるかを説明します。この議論に続いて、このようなシステムが異なる量子状態を圧縮する能力と、0と1の画像を圧縮する能力を示すために、2つの例を挙げます。
目次#
チュートリアルは、以下のように構成されています。
オートエンコーダーとは何か?
量子オートエンコーダー
量子オートエンコーダーの構成要素
損失関数の選択
オートエンコーダーの構築
簡単な例:領域の壁
ノイズがある数字の画像のための量子オートエンコーダー
量子オートエンコーダーの応用
参考文献
1. オートエンコーダーとは何か?#
古典的オートエンコーダー (CAE) はニューラルネットワークの一種で、表現学習を利用して入力から情報を効率的に圧縮し、符号化するためによく使われるアーキテクチャーです。圧縮した後、デコーダーを使ってデータを復元することができます
一般的なオートエンコーダーは、図 1に示すように 3 つの層に分けられています。
Figure 1: Example of a Classical Autoencoder which includes the input, bottleneck and output layer.
最初の層は入力層 (1)と呼ばれ、長さ \(n\) のデータを入力する層です。
入力データはエンコーダーを通過し、次の層に移動します。この層はノード数が少ないか、次元が小さく、ボトルネック層 (2) と呼ばれます。入力層は、このプロセスを通じて圧縮されます。一般的なCAEでは、いくつかの層を持つことがあります。
最後の層は出力層 (3) と呼ばれます。ここでは、圧縮されたデータから、デコーダーの処理によって元のサイズである \(n\) に復元されます。
このように、入力データをCAEに通すことで、入力データからできるだけ多くの情報を保持したまま、ボトルネック層に見られるように入力データの次元を小さくできるのです。この特徴から、CAEの一般的な用途としては、画像ノイズ除去、異常検出、顔認識装置などが挙げられます。古典的なオートエンコーダの詳細については、[1] を参照してください。
2. 量子オートエンコーダー#
CAEに対応する量子オートエンコーダーを定義することもできます。CAEと同様に、量子オートエンコーダーはニューラルネットワークの入力(この場合は量子状態)の次元を小さくすることを目的としています。図2にそのイメージを示します。
図2:量子オートエンコーダの図解。ここでは、回路が入力状態、ボトルネック状態、出力状態を持つという、CAEとの類似性を見ることができます。
古典的なものと同じように、この回路は3つの層で構成されています。まず、圧縮したい状態 \(|psi>\) (これは \(n\) 個の量子ビットを含む) を入力します。これが入力層 (1) です。
この回路はエンコーダーとして働き、量子状態を「圧縮」し、量子ビットの次元を \(n-k\) まで減少させます。圧縮された新しい状態は \(|psi_{comp}> \otimes |0>^{\otimes k}\) という形式で、ここで \(|psi_{comp}>\) は \(n-k\) 個の量子ビットを含みます。
このパラメーター化された回路は、量子オートエンコーダーのノードとなるパラメーターのセットに依存します。学習プロセスを通じて、これらのパラメーターは損失関数を最適化するために更新されます。
残りの \(k\) 量子ビットは無視します。これがボトルネック層(2)であり、入力状態は圧縮された状態です。
最後の層は \(k\) 個の量子ビット (全て \(|0\rangle\) 状態) を追加し、圧縮された状態と新しい量子ビットの間に別のパラメーター化された回路を適用します。このパラメーター化された回路はデコーダーとして機能し、新しい量子ビットを使って圧縮された状態から入力状態を再構成します。デコーダーの後、状態が出力層 (3) に移動する際に元の状態を保持します。
3. 量子オートエンコーダーの構成要素#
量子オートエンコーダーを構築する前に、いくつかの微妙な点について注意しなければなりません。
まず、Qiskitを使ってオートエンコーダーを実装するとき、量子回路の途中で量子ビットを導入したり無視したりできないことに注意します。
このため、回路の最初に参照状態と補助量子ビット (その役割は後のセクションで説明します) を含めなければなりません。
したがって、入力状態は、入力状態、参照状態、1つの補助量子ビット、そして測定を行うための古典的なレジスター (次のセクションで説明します) で構成されることになります。これを絵で表したのが図3です。
図3:量子オートエンコーダーの入力状態の図解。補助量子ビット、参照状態、古典レジスターも、回路の後半まで使用されないにもかかわらず、回路の最初に含めなければならないことに注意してください。
4. 損失関数の選択#
量子オートエンコーダーの訓練に使用する、入力状態を返すためのコスト関数を定義します。ここで少し数学が絡んでくるので、興味のない方はこのセクションを飛ばしてください。
この関数は、量子オートエンコーダーの入力と出力の状態の間の忠実度を最大化しようとするもので、[2] で定義されているように、コスト関数を取ります。
まず、サブシステム \(A\) と \(B\) を定義し、それぞれ \(n\) と \(k\) の量子ビットを格納することにします。\(B'\) は参照空間です。我々は、サブシステム \(A\) を潜在空間と呼び、圧縮された量子ビットの状態を格納します。また、 \(B\) をゴミ空間と呼び、圧縮時に無視された量子ビットを格納します。
したがって、入力状態 \(|psi_{AB}>\) は \(n + k\) 個の量子ビットを含んでいます。参照状態 \(|a>_{B'}\) を含む参照空間 \(B'\) を定義します。この空間には、デコーダーで使用する追加の \(k\) 量子ビットが含まれます。これらの全てのサブシステムを図3に示します。
パラメーター化された回路を \(U(\theta)\) と定義し、これをエンコーダーとして使用することにします。しかし、パラメーター化された回路の構造やパラメーターは今のところ不明であり、異なる入力状態に対して変化する可能性があります。入力状態を圧縮するためのパラメーターを決定するために、パラメーター \(\theta\) の値を調整することによって、状態を最大限に圧縮するようにデバイスを訓練する必要があります。デコーダーには \(U^{\dagger}(\theta)\) を使用します。
したがって、我々の目標は、入力と出力の状態の間の忠実度を最大化すること、つまり、以下を最大化します。
ここで
この忠実度は、パラメーター化された回路のパラメーター \(\theta\) を調整することで最大化することができます。しかし、この忠実度を決定するのは複雑で、2つの状態の忠実度を計算するために大量のゲートを必要とすることがあります。つまり、量子ビットの数が大きくなればなるほど、より多くのゲートが必要となり、結果として回路が深くなってしまいます。そこで私たちは、入力と出力の状態を比較する別の方法を探します。
[2] で示したように、最適な圧縮状態を決定するより簡単な方法は、ゴミ状態と参照状態との間でスワップゲートを実行することです。これらの状態は通常、より少ない数の量子ビットを持ち、したがって、必要なゲートの量が少ないため、比較しやすくなっています。[2] で示したように、これら2つの状態の忠実度を最大化することは、入力と出力の状態の忠実度を最大化することと等しく、したがって、入力回路の最適な圧縮を決定できるのです。
参照状態を固定すると、コスト関数はゴミ状態の関数となり、次のように示されます。
学習プロセスを通して、エンコーダーのパラメーター \(\theta\) を調整し、スワップテスト (後述) を行い、ゴミ状態と参照状態の間の忠実度を決定します。その際、補助量子ビットを追加する必要があります。この量子ビットはスワップテストの間中使用され、ゴミ状態と参照状態の全体的な忠実度を決定するために測定されます。これが、前節で回路の初期化時に補助量子ビットと古典レジスターの両方を含めた理由です。
SWAP テスト#
SWAPテストとは、各量子ビットに対してCNOTゲートを適用し、2つの状態を比較するためによく使われる手順です (詳しくは[3]を参照してください)。回路を \(M\) 回走らせ、SWAPテストを適用し、次に補助量子ビットを測定します。このとき、状態 \(|1\rangle\) である状態の数を使って計算します:
ここで、 \(L\) は \(|1\rangle\) 状態の数です。[3]で示したように、この関数を最大化することは、比較する2つの状態が同一であることに対応します。したがって、この関数を最大化すること、すなわち \(\frac{2}{M}L\) を最小化することを目指します。したがって、この値が我々のコスト関数となります。
5. 量子オートエンコーダーAnsatz の構築#
まず、IBMのQiskitを実装して、量子オートエンコーダーを構築します。まず、必要なライブラリーをインポートし、シードを指定するところから始めます。
[1]:
import json
import time
import warnings
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
from qiskit import ClassicalRegister, QuantumRegister
from qiskit import QuantumCircuit
from qiskit.circuit.library import RealAmplitudes
from qiskit.quantum_info import Statevector
from qiskit_algorithms.optimizers import COBYLA
from qiskit_algorithms.utils import algorithm_globals
from qiskit_machine_learning.circuit.library import RawFeatureVector
from qiskit_machine_learning.neural_networks import SamplerQNN
algorithm_globals.random_seed = 42
まず、量子オートエンコーダーのためのパラメーター化されたansatzを定義することから始めます。この回路はパラメーターを調整することで、ゴミ状態と参照状態の間の忠実度を最大にできる、パラメーター化された回路となります。
パラメーター化された回路#
私たちのエンコーダーに使用するパラメーター化された回路は、Qiskitで利用可能なRealAmplitude Ansatzです。この回路を選んだ理由の1つは、2ローカル回路であり、準備された量子状態は実振幅のみを持ち、実装が困難で深い回路になってしまう各量子ビット間の完全な接続性に依存しないからです。
この回路では、繰り返しパラメーターを reps=5 とし、パラメーター数を増やすことでより柔軟な回路を実現しています。
[2]:
def ansatz(num_qubits):
return RealAmplitudes(num_qubits, reps=5)
このansatzを \(5\) 量子ビットで描いて見ましょう。
[3]:
num_qubits = 5
circ = ansatz(num_qubits)
circ.decompose().draw("mpl")
[3]:

次に、このエンコーダーを圧縮したい状態に適用します。この例では、最初の \(5\) 個の量子ビットの状態を \(3\) 個の量子ビット潜在状態 (\(n = 3\)) と \(2\) 個の量子ビットゴミ空間 (\(k = 2\)) に分割しています。
前のセクションで説明したように、私たちの回路には \(2\) 量子ビットの参照空間と、参照状態とゴミ状態の間でスワップテストを行うための補助量子ビットも含める必要があります。したがって、私たちの回路には合計で \(2 + 3 + 2 + 1 = 8\) 個の量子ビットと \(1\) 個の古典レジスターが含まれることになります。
状態を初期化した後、パラメーター化された回路を適用します。
続いて、初期状態を潜在空間 (圧縮された状態) とゴミ空間 (無視する部分) に分割し、参照状態とゴミ空間とのスワップテストを行います。そして、最後の量子ビットを測定して、参照状態とゴミ状態の間の忠実度を決定します。これを絵で表したのが、以下の図4です。
図4:学習過程における量子オートエンコーダーの例。ゴミ空間と参照空間の間の忠実度を判断するためにスワップテストを用います。
ここでは、 \(5\) 量子ビットのドメインウォール状態 \(|00111\rangle\) に対して上記の回路を実装するための関数を定義し、その例を以下に示します。ここで、量子ビット \(5\) と \(6\) は参照状態、 \(0, 1, 2, 3, 4\) は圧縮したい初期状態、量子ビット \(7\) はスワップテストに使用する補助的な量子ビットです。また、スワップテストにおける量子ビット \(7\) の結果を測定するための古典的なレジスターも含まれています。
[4]:
def auto_encoder_circuit(num_latent, num_trash):
qr = QuantumRegister(num_latent + 2 * num_trash + 1, "q")
cr = ClassicalRegister(1, "c")
circuit = QuantumCircuit(qr, cr)
circuit.compose(ansatz(num_latent + num_trash), range(0, num_latent + num_trash), inplace=True)
circuit.barrier()
auxiliary_qubit = num_latent + 2 * num_trash
# swap test
circuit.h(auxiliary_qubit)
for i in range(num_trash):
circuit.cswap(auxiliary_qubit, num_latent + i, num_latent + num_trash + i)
circuit.h(auxiliary_qubit)
circuit.measure(auxiliary_qubit, cr[0])
return circuit
num_latent = 3
num_trash = 2
circuit = auto_encoder_circuit(num_latent, num_trash)
circuit.draw("mpl")
[4]:
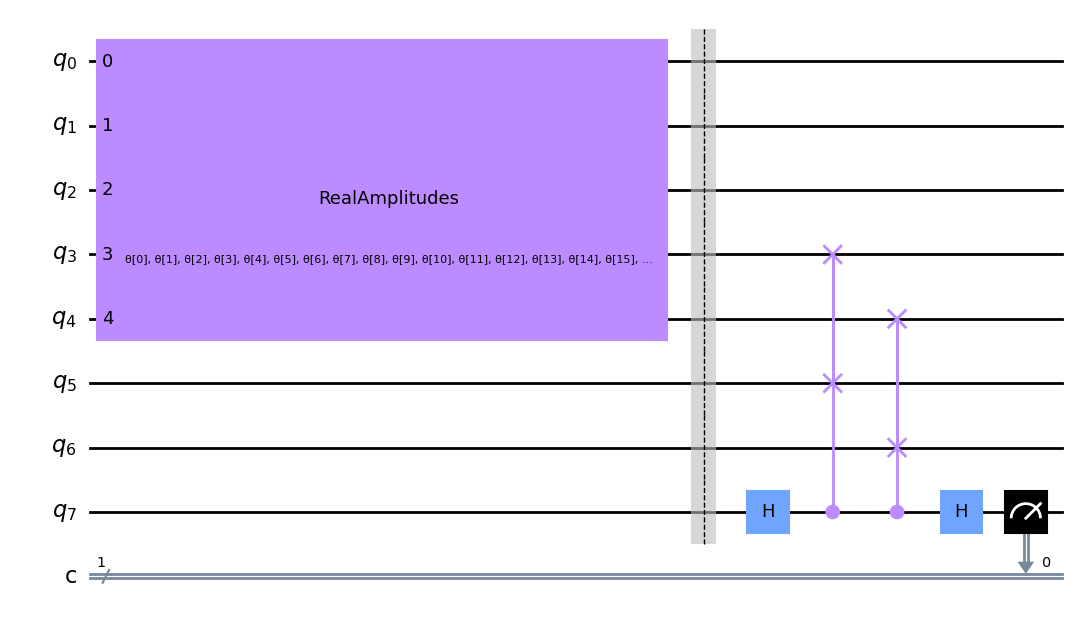
元の入力状態を復元するためには、スワップテスト後にパラメーター化された回路の随伴行列を適用する必要があります。しかし、学習中はゴミ状態と参照状態にしか興味がありません。したがって、最初の入力を再構成したいときまで、圧縮後のゲートを除外することができます。
量子オートエンコーダーを構築したら、次は量子オートエンコーダーを訓練して状態を圧縮し、コスト関数を最大化し、パラメータ \(\theta\) を決定する必要があります。
6. 簡単な例:ドメインウォール・オートエンコーダー#
まず、簡単な例から始めましょう。ドメインウォールとして知られる状態は、 \(5\) 量子ビットに対して \(|00111\rangle\) によって与えられます。ここで、この状態を \(5\) 量子ビットから \(3\) 量子ビットに圧縮しようと試み、残りの量子ビットはゴミ状態 \(|00\rangle\) に入れましょう。 以下のドメインウォール状態を構築する関数を作成できます。
[5]:
def domain_wall(circuit, a, b):
# Here we place the Domain Wall to qubits a - b in our circuit
for i in np.arange(int(b / 2), int(b)):
circuit.x(i)
return circuit
domain_wall_circuit = domain_wall(QuantumCircuit(5), 0, 5)
domain_wall_circuit.draw("mpl")
[5]:
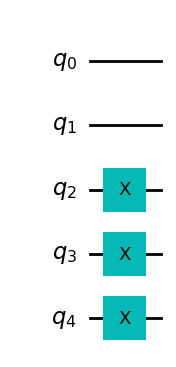
さて、この状態を5量子ビットから3量子ビット (量子ビット0、1、2) に圧縮し、ゴミ空間の残りの量子ビット (量子ビット3、4) は |00> 状態になるようにオートエンコーダーを学習させましょう。
我々は、セクション4で説明するように、損失関数で使用する回路を作成し、我々の特定のAutoEncoder関数に対するスワップテストを使用して、以下の2つの状態間の忠実度を決定します。スワップテストの詳細については、[1] を参照してください。
[6]:
ae = auto_encoder_circuit(num_latent, num_trash)
qc = QuantumCircuit(num_latent + 2 * num_trash + 1, 1)
qc = qc.compose(domain_wall_circuit, range(num_latent + num_trash))
qc = qc.compose(ae)
qc.draw("mpl")
[6]:

次に、量子ニューラルネットワークを作成し、その回路をパラメーターとして渡します。このネットワークは、ネットワークの出力をどのように出力形状にマッピングするかを決定する、解釈関数を受け取らなければならないことに注意してください。量子ビットは1つだけなので、ネットワークの出力は \(0\) か \(1\) のビット列となり、出力形状は \(2\) となります (これは可能な結果の数です)。次に、恒等写像を導入します。ネットワークの出力は、解釈マッピングされたビット文字列を得る確率のベクトルです。つまり、 \(0\) や \(1\) を得る確率が得られ、これはまさに我々が求めているものです。コスト関数では、\(1\) を得る確率を利用し、 \(1\) につながる結果にペナルティを与えることで、ゴミ空間と参照空間の間の忠実度を最大化します。
[7]:
# Here we define our interpret for our SamplerQNN
def identity_interpret(x):
return x
qnn = SamplerQNN(
circuit=qc,
input_params=[],
weight_params=ae.parameters,
interpret=identity_interpret,
output_shape=2,
)
次に、コスト関数を作成します。前のセクションで説明したように、我々の目的は:math:frac{2}{M}L を最小化することで、これは最終的に量子ビットが \(|1\rangle\) 状態となる確率の2倍です。したがって、量子ビット7で \(|1\rangle\) を得る確率を最小にしたいのです。
また、コスト関数は、各コスト関数評価時の目的値をプロットすることになります。
[8]:
def cost_func_domain(params_values):
probabilities = qnn.forward([], params_values)
# we pick a probability of getting 1 as the output of the network
cost = np.sum(probabilities[:, 1])
# plotting part
clear_output(wait=True)
objective_func_vals.append(cost)
plt.title("Objective function value against iteration")
plt.xlabel("Iteration")
plt.ylabel("Objective function value")
plt.plot(range(len(objective_func_vals)), objective_func_vals)
plt.show()
return cost
ここでは、Hilbert空間の次元を \(5\) 量子ビットから \(3\) に減らし、ゴミ空間は \(|00\rangle\) の状態のままにして、オートエンコーダーを学習させます。パラメーター \(\theta\) をランダムな値に初期設定し、COBYLAオプティマイザーを使用してコスト関数を最小化するようにこれらのパラメーターをチューニングします。
[9]:
opt = COBYLA(maxiter=150)
initial_point = algorithm_globals.random.random(ae.num_parameters)
objective_func_vals = []
# make the plot nicer
plt.rcParams["figure.figsize"] = (12, 6)
start = time.time()
opt_result = opt.minimize(cost_func_domain, initial_point)
elapsed = time.time() - start
print(f"Fit in {elapsed:0.2f} seconds")
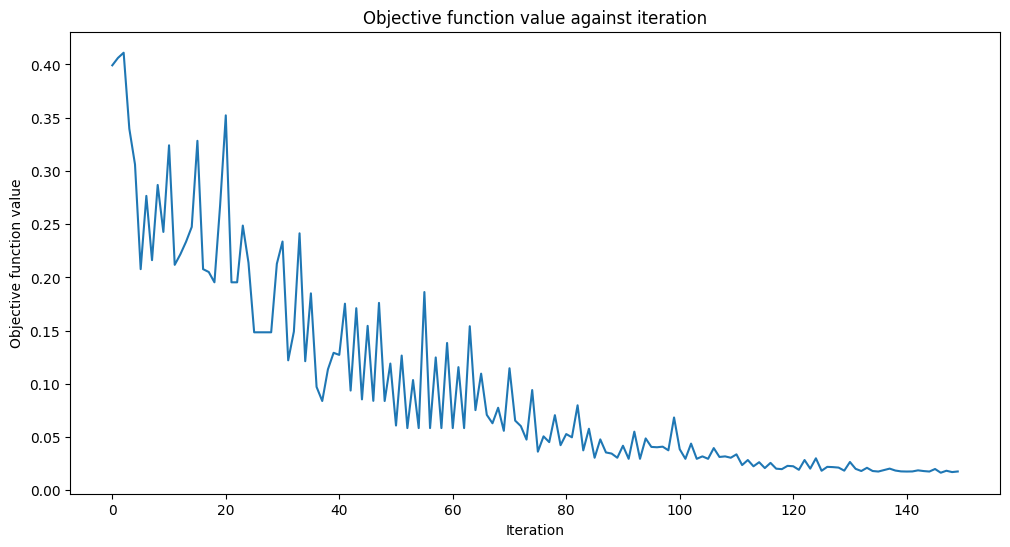
Fit in 18.48 seconds
どうやら収束したようです! 量子オートエンコーダーを学習させた後、それを構築し、状態をどれだけ圧縮できるかを見てみましょう。
これを行うには、まずオートエンコーダーを \(5\) 量子ビット・ドメインウォール状態に適用します。この状態を適用した後、圧縮された状態は \(|00\rangle\) のような形になるはずです。したがって、最後の2つの量子ビットをリセットしても、全体的な状態に影響を与えることはありません。
リセット後、デコーダー (エンコーダーのエルミート共役) を適用し、忠実度を決定することによって初期状態と比較します。忠実度が1であれば、オートエンコーダーはドメインウォールのすべての情報をより小さな量子ビットの集合に効率的にエンコードしたことになり、デコード時には元の状態を保持することになります!
まず、量子オートエンコーダのトレーニングで得たパラメータを用いて、ドメインウォールの状態に我々の回路を適用してみましょう (この回路にはバリアーが含まれていますが、これは量子オートエンコーダーの実装には必要なく、回路の異なるセクションの間を決定するために使用されます) 。
[10]:
test_qc = QuantumCircuit(num_latent + num_trash)
test_qc = test_qc.compose(domain_wall_circuit)
ansatz_qc = ansatz(num_latent + num_trash)
test_qc = test_qc.compose(ansatz_qc)
test_qc.barrier()
test_qc.reset(4)
test_qc.reset(3)
test_qc.barrier()
test_qc = test_qc.compose(ansatz_qc.inverse())
test_qc.draw("mpl")
[10]:
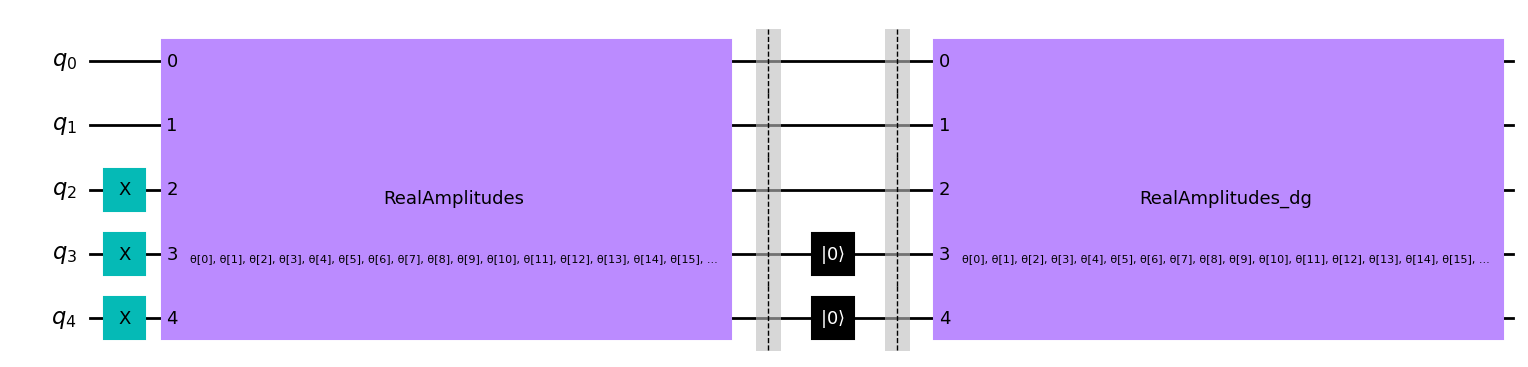
ここで、学習で得られたパラメーター値を代入します。
[11]:
test_qc = test_qc.assign_parameters(opt_result.x)
それでは、ドメインウォール状態と出力回路の状態ベクトルを取得し、忠実度を計算してみましょう!
[12]:
domain_wall_state = Statevector(domain_wall_circuit).data
output_state = Statevector(test_qc).data
fidelity = np.sqrt(np.dot(domain_wall_state.conj(), output_state) ** 2)
print("Fidelity of our Output State with our Input State: ", fidelity.real)
Fidelity of our Output State with our Input State: 0.9832814006314854
このように、オートエンコーダーは入力状態の情報をすべて保持したまま、データセットを圧縮しているのです。
次に、このような量子オートエンコーダーを、ノイズを含むより複雑なデータセット、例えば数字の0と1の画像に適用できるかどうか見てみましょう。
7. デジタル圧縮のための 量子オートエンコーダー#
また、データセットを圧縮するために、手書きの数字の集合のような、より複雑な例にも量子オートエンコーダーを適用することができます。以下では、実際に量子オートエンコーダーを訓練してこのような例を圧縮できることを示し、量子コンピューターでより効率的にデータを保存できるようにします。
このチュートリアルでは、0と1を含むノイズの多いデータセットに対して、量子オートエンコーダーを構築します(下図)。
各画像は \(32\) ピクセルを含み、振幅エンコーディングによって \(5\) 個の量子ビットにエンコードされます。これはQiskit Machine Learning の RawFeatureVector 特徴量マップを使用して行うことができます。
[13]:
def zero_idx(j, i):
# Index for zero pixels
return [
[i, j],
[i - 1, j - 1],
[i - 1, j + 1],
[i - 2, j - 1],
[i - 2, j + 1],
[i - 3, j - 1],
[i - 3, j + 1],
[i - 4, j - 1],
[i - 4, j + 1],
[i - 5, j],
]
def one_idx(i, j):
# Index for one pixels
return [[i, j - 1], [i, j - 2], [i, j - 3], [i, j - 4], [i, j - 5], [i - 1, j - 4], [i, j]]
def get_dataset_digits(num, draw=True):
# Create Dataset containing zero and one
train_images = []
train_labels = []
for i in range(int(num / 2)):
# First we introduce background noise
empty = np.array([algorithm_globals.random.uniform(0, 0.1) for i in range(32)]).reshape(
8, 4
)
# Now we insert the pixels for the one
for i, j in one_idx(2, 6):
empty[j][i] = algorithm_globals.random.uniform(0.9, 1)
train_images.append(empty)
train_labels.append(1)
if draw:
plt.title("This is a One")
plt.imshow(train_images[-1])
plt.show()
for i in range(int(num / 2)):
empty = np.array([algorithm_globals.random.uniform(0, 0.1) for i in range(32)]).reshape(
8, 4
)
# Now we insert the pixels for the zero
for k, j in zero_idx(2, 6):
empty[k][j] = algorithm_globals.random.uniform(0.9, 1)
train_images.append(empty)
train_labels.append(0)
if draw:
plt.imshow(train_images[-1])
plt.title("This is a Zero")
plt.show()
train_images = np.array(train_images)
train_images = train_images.reshape(len(train_images), 32)
for i in range(len(train_images)):
sum_sq = np.sum(train_images[i] ** 2)
train_images[i] = train_images[i] / np.sqrt(sum_sq)
return train_images, train_labels
train_images, __ = get_dataset_digits(2)
Math:5`量子ビットに画像をエンコードした後、この状態を :math:`3 量子ビットに圧縮するために量子オートエンコーダーの学習を開始します。
前の例のステップを繰り返し、再びゴミ空間と潜在空間間のスワップテストに基づいたコスト関数を書きます。入力状態とゴミ空間が同じ量の量子ビットを含むので、前の例で与えられたのと同じオートエンコーダー関数を使用することもできます。
1桁の数字を入力し、オートエンコーダーの回路を以下に示します。
[14]:
num_latent = 3
num_trash = 2
fm = RawFeatureVector(2 ** (num_latent + num_trash))
ae = auto_encoder_circuit(num_latent, num_trash)
qc = QuantumCircuit(num_latent + 2 * num_trash + 1, 1)
qc = qc.compose(fm, range(num_latent + num_trash))
qc = qc.compose(ae)
qc.draw("mpl")
[14]:

ここでも、スワップテストが量子ビット \(3\), \(4\), \(5\), \(6\) に対して行われ、コスト関数の値を決定していることがわかります。
[15]:
def identity_interpret(x):
return x
qnn = SamplerQNN(
circuit=qc,
input_params=fm.parameters,
weight_params=ae.parameters,
interpret=identity_interpret,
output_shape=2,
)
我々は、数字データセットの参照空間とゴミ空間の間のスワップテストに基づいて、コスト関数を構築します。これを行うには、再びQiskit Machine Learning のCircuitQNNネットワークを使用し、最終的な量子ビットが \(|1\rangle\) 状態になる確率を測定しているのと同じ解釈関数を使用します。
[16]:
def cost_func_digits(params_values):
probabilities = qnn.forward(train_images, params_values)
cost = np.sum(probabilities[:, 1]) / train_images.shape[0]
# plotting part
clear_output(wait=True)
objective_func_vals.append(cost)
plt.title("Objective function value against iteration")
plt.xlabel("Iteration")
plt.ylabel("Objective function value")
plt.plot(range(len(objective_func_vals)), objective_func_vals)
plt.show()
return cost
モデルの学習には長い時間がかかる可能性があるため、すでにいくつかの反復で事前学習したモデルがあり、事前学習済みの重みを保存してあります。 initial_point に学習済みの重みのベクトルを設定することで、その時点から学習を継続することにします。
[17]:
with open("12_qae_initial_point.json", "r") as f:
initial_point = json.load(f)
このコスト関数を最小化することで、ノイズの多い画像を圧縮するために必要なパラメーターを決定できるのです。それでは、画像をエンコードしてみましょう。
[18]:
opt = COBYLA(maxiter=150)
objective_func_vals = []
# make the plot nicer
plt.rcParams["figure.figsize"] = (12, 6)
start = time.time()
opt_result = opt.minimize(fun=cost_func_digits, x0=initial_point)
elapsed = time.time() - start
print(f"Fit in {elapsed:0.2f} seconds")
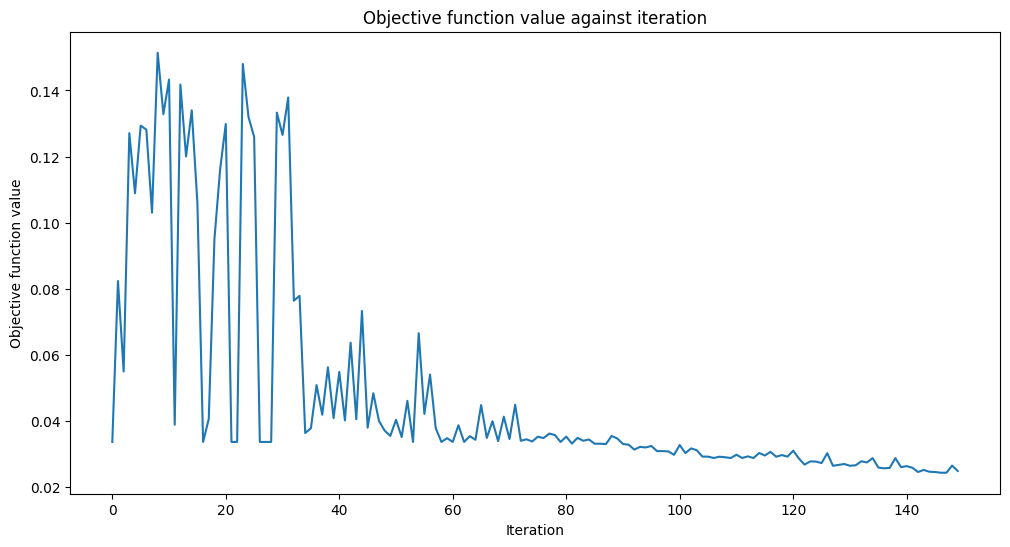
Fit in 40.59 seconds
収束したようです!
では、学習期間中に得られたパラメーターを使って、エンコーダーとデコーダーを構築してみましょう。この回路を新しいデータセットに適用した後、入力データと出力データを比較し、圧縮の間、画像を効率的に保持できたかどうかを確認します!
[19]:
# Test
test_qc = QuantumCircuit(num_latent + num_trash)
test_qc = test_qc.compose(fm)
ansatz_qc = ansatz(num_latent + num_trash)
test_qc = test_qc.compose(ansatz_qc)
test_qc.barrier()
test_qc.reset(4)
test_qc.reset(3)
test_qc.barrier()
test_qc = test_qc.compose(ansatz_qc.inverse())
# sample new images
test_images, test_labels = get_dataset_digits(2, draw=False)
for image, label in zip(test_images, test_labels):
original_qc = fm.assign_parameters(image)
original_sv = Statevector(original_qc).data
original_sv = np.reshape(np.abs(original_sv) ** 2, (8, 4))
param_values = np.concatenate((image, opt_result.x))
output_qc = test_qc.assign_parameters(param_values)
output_sv = Statevector(output_qc).data
output_sv = np.reshape(np.abs(output_sv) ** 2, (8, 4))
fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.imshow(original_sv)
ax1.set_title("Input Data")
ax2.imshow(output_sv)
ax2.set_title("Output Data")
plt.show()
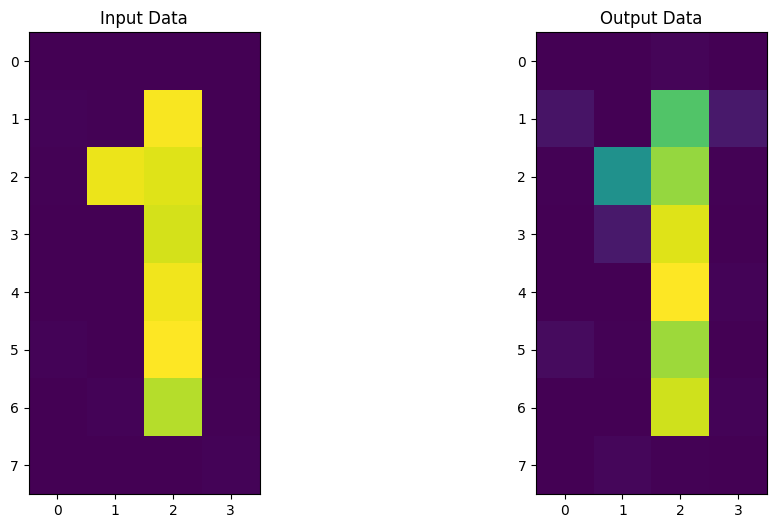
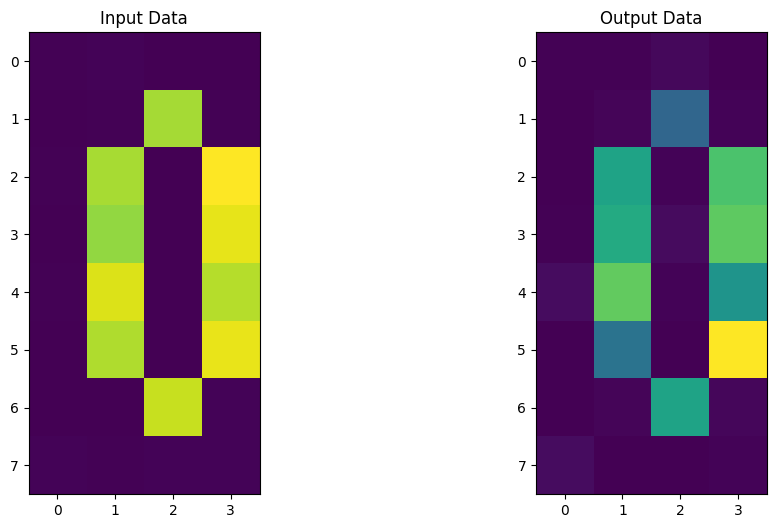
この量子オートエンコーダーは、数字のエンコードもできるようです。さあ、次はあなたが量子オートエンコーダーを作り、圧縮するためのアイデアやデータセットを考える番です。
8. 量子オートエンコーダーの応用#
量子オートエンコーダは、以下のような様々な用途に使用することができます。
デジタル圧縮: 情報をより少ない量の量子ビットにエンコードすることができます。これは、より小さな量子ビットのシステムは、ノイズの影響を受けにくいので、近い将来の量子デバイスに非常に有益です。
ノイズ除去: 量子オートエンコーダーを使って、初期量子状態や符号化されたデータから関連する特徴を抽出し、追加されているノイズを無視することができます。
量子化学: 量子オートエンコーダーは、ハバードモデルのようなシステムのAnsatzとして使用することができます。これは、分子内の電子-電子相互作用を記述するために一般的に使用されます。
9. 参考文献#
A wikipedia page on Autoencoder: https://en.wikipedia.org/wiki/Autoencoder
Romero, Jonathan, Jonathan P. Olson, and Alan Aspuru-Guzik. “Quantum autoencoders for efficient compression of quantum data.” Quantum Science and Technology 2.4 (2017): 045001.
Swap Test Algorithm: https://en.wikipedia.org/wiki/Swap_test
[20]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.22.2 |
qiskit-aer | 0.11.1 |
qiskit-machine-learning | 0.6.0 |
| System information | |
| Python version | 3.8.13 |
| Python compiler | Clang 12.0.0 |
| Python build | default, Oct 19 2022 17:54:22 |
| OS | Darwin |
| CPUs | 10 |
| Memory (Gb) | 64.0 |
| Thu Nov 10 23:26:05 2022 GMT | |
This code is a part of Qiskit
© Copyright IBM 2017, 2022.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.