注釈

このページは docs/tutorials/03_quantum_kernel.ipynb から生成されました。

量子カーネル法機械学習#

概要#

機械学習の一般的なタスクは、データのパターンを見つけて学習することです。多くのデータセットでは、データポイントは高次元の特徴空間でよりよく理解されます。これは、 カーネル・メソッド として知られる一連の機械学習アルゴリズムの背後にある基本原理です。

このノートブックでは、 qiskit-machine-learning を使用して量子カーネルを定義する方法と、これらをさまざまなアルゴリズムにプラグインして分類とクラスタリングの問題を解決する方法を学習します。

このチュートリアルで使用されているすべての例は、次のリファレンスペーパーに基づいています。 Supervised learning with quantum enhanced feature spaces

このコンテンツの構造は以下のとおりです。

はじめに
分類
クラスタリング
カーネル主成分解析
結論

1. はじめに#

1.1. 機械学習のカーネル・メソッド#

カーネル法は、高次元特徴量空間で動作するカーネル関数を使用するパターン分析アルゴリズムのコレクションです。カーネル法の最もよく知られた応用は サポートベクターマシン（SVM） で、分類タスクによく使われる教師あり学習アルゴリズムです。SVMの主な目的は、与えられたデータ・ポイントをクラスに分離するための決定境界を見つけることです。このデータ空間が線形分離可能でない場合、SVMはこれらの境界を見つけるためにカーネルを使用することで利益を得ることができます。

形式的には、決定境界は高次元空間の超平面です。カーネル関数は、入力データをこの高次元空間に暗黙的にマッピングし、与えられた問題をより簡単に解くことがでます。言い換えれば、カーネルは元々非線形分離可能であったデータ分布を線形分離可能な問題にすることができます。これは「カーネル・トリック」として知られる効果です。

カーネルベースの教師なしアルゴリズムにも、例えばクラスタリングの文脈で使われるケースがあります。 スペクトル・クラスタリング は、データ点をグラフのノードとして扱う手法であり、クラスタリング・タスクは、ノードがクラスタを形成するために容易に分離できる空間にマッピングされるグラフ分割問題として見なされます。

1.2 . カーネル関数#

数学的には、カーネル関数は次のとおりです：

\(k(\vec{x}_i, \vec{x}_j) = \langle f(\vec{x}_i), f(\vec{x}_j) \rangle\)

ここで、 * \(k\) はカーネル関数、 * \(\vec{x}_i, \vec{x}_j\) は \(n\) 次元の入力、 * \(f\) は \(n\) 次元から \(m\) 次元の空間への写像、 * \(\langle a,b \rangle\) は内積を表します。

有限データを考慮する場合、カーネル関数は次のような行列として表現することができます。

\(K_{ij} = k(\vec{x}_i,\vec{x}_j)\).

1.3 量子カーネル#

量子カーネル機械学習の背後にある主なアイデアは、量子特徴量マップを活用してカーネルトリックを実行することです。この場合、量子カーネルは、量子特徴量マップ \(\phi(\vec{x})\) を使用して古典的特徴量ベクトル \(\vec{x}\) をヒルベルト空間にマッピングすることによって作成されます。数学的には以下です:

\(K_{ij} = \left| \langle \phi(\vec{x}_i)| \phi(\vec{x}_j) \rangle \right|^{2}\)

ここで、 * \(K_{ij}\) はカーネル行列、 * \(\vec{x}_i, \vec{x}_j\) は \(n\) 次元の入力、 * \(\phi(\vec{x})\) は量子特徴量マップ、 * \(\left| \langle a|b \rangle \right|^{2}\) は 2 つの量子状態 \(a\) と \(b\) の重なりを表します。

以下の例でわかるように、量子カーネルは、SVM やクラスタリングアルゴリズムなどの一般的な古典的なカーネル学習アルゴリズムに接続できます。これらは、このチュートリアルで説明する qiskit-machine-learning によって提供される QSVC class のような新しい量子カーネルメソッドや、後のペガソス QSVC および量子カーネルトレーニングで示される他のメソッドでも利用できます。

例を紹介する前に、再現性を確保するためにグローバル・シードをセットアップします。

[1]:

from qiskit_algorithms.utils import algorithm_globals

algorithm_globals.random_seed = 12345

2.分類#

このセクションでは、 qiskit-machine-learning を使用した量子カーネル分類ワークフローについて説明します。

2.1. データセットの定義#

この例では、 paper の中で説明されているように、 ad hoc dataset を使用します。

データセットの次元を定義し、訓練とテストのサブセットを取得します。

[2]:

from qiskit_machine_learning.datasets import ad_hoc_data

adhoc_dimension = 2
train_features, train_labels, test_features, test_labels, adhoc_total = ad_hoc_data(
    training_size=20,
    test_size=5,
    n=adhoc_dimension,
    gap=0.3,
    plot_data=False,
    one_hot=False,
    include_sample_total=True,
)

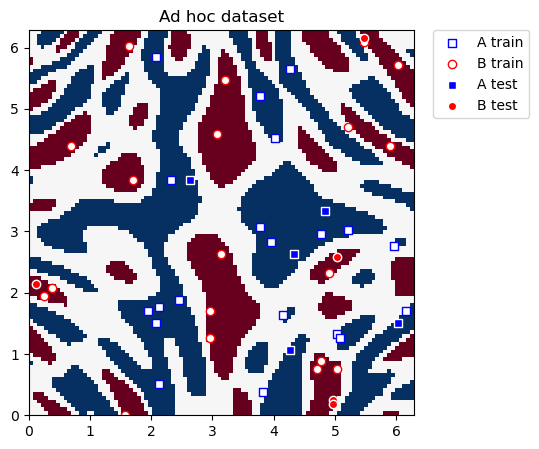
このデータセットは2次元で、 \(x\) と \(y\) 座標で表されます。 AとBの2つのクラスラベルがあります。データセットをプロットするためのユーティリティ関数を定義します。

[3]:

import matplotlib.pyplot as plt
import numpy as np


def plot_features(ax, features, labels, class_label, marker, face, edge, label):
    # A train plot
    ax.scatter(
        # x coordinate of labels where class is class_label
        features[np.where(labels[:] == class_label), 0],
        # y coordinate of labels where class is class_label
        features[np.where(labels[:] == class_label), 1],
        marker=marker,
        facecolors=face,
        edgecolors=edge,
        label=label,
    )


def plot_dataset(train_features, train_labels, test_features, test_labels, adhoc_total):

    plt.figure(figsize=(5, 5))
    plt.ylim(0, 2 * np.pi)
    plt.xlim(0, 2 * np.pi)
    plt.imshow(
        np.asmatrix(adhoc_total).T,
        interpolation="nearest",
        origin="lower",
        cmap="RdBu",
        extent=[0, 2 * np.pi, 0, 2 * np.pi],
    )

    # A train plot
    plot_features(plt, train_features, train_labels, 0, "s", "w", "b", "A train")

    # B train plot
    plot_features(plt, train_features, train_labels, 1, "o", "w", "r", "B train")

    # A test plot
    plot_features(plt, test_features, test_labels, 0, "s", "b", "w", "A test")

    # B test plot
    plot_features(plt, test_features, test_labels, 1, "o", "r", "w", "B test")

    plt.legend(bbox_to_anchor=(1.05, 1), loc="upper left", borderaxespad=0.0)
    plt.title("Ad hoc dataset")

    plt.show()

さて分類のためのデータセットを実際にプロットします。

[4]:

plot_dataset(train_features, train_labels, test_features, test_labels, adhoc_total)

../_images/tutorials_03_quantum_kernel_10_0.png

2.2. 量子カーネルの定義#

次のステップは、このデータを分類するのに役立つ量子カーネルインスタンスを作成することです。

FidelityQuantumKernel class を使用し、2つの入力引数をコンストラクターに渡します:

feature_map: この場合、2 qubit の ZZFeatureMap です。
fidelity: この場合、 ComputeUncompute fidelity サブルーチンは、 Sampler primitive を利用します。

注意: Sampler または Fidelity インスタンスを渡さない場合は、Sampler と ComputeUncompute クラス (qiskit.primitives にあります) はデフォルトで作成されます。

[5]:

from qiskit.circuit.library import ZZFeatureMap
from qiskit.primitives import Sampler
from qiskit_algorithms.state_fidelities import ComputeUncompute
from qiskit_machine_learning.kernels import FidelityQuantumKernel

adhoc_feature_map = ZZFeatureMap(feature_dimension=adhoc_dimension, reps=2, entanglement="linear")

sampler = Sampler()

fidelity = ComputeUncompute(sampler=sampler)

adhoc_kernel = FidelityQuantumKernel(fidelity=fidelity, feature_map=adhoc_feature_map)

2.3. SVCによる分類#

量子カーネルは、 scikit-learn の SVC algorithm のような古典的なカーネルメソッドに接続することができます。このアルゴリズムでは、2つの方法でカスタムカーネルを定義することができます：

カーネルを 呼び出し可能な関数 として提供する
カーネル行列 を事前に計算する

呼び出し可能な関数としてのカーネル#

SVC モデルを定義し、量子カーネルの evaluate 関数を呼び出し可能として直接渡します。モデルが作成されたら、トレーニングデータセットに対して fit メソッドを呼び出してモデルをトレーニングし、モデルの精度を score で評価します。

[6]:

from sklearn.svm import SVC

adhoc_svc = SVC(kernel=adhoc_kernel.evaluate)

adhoc_svc.fit(train_features, train_labels)

adhoc_score_callable_function = adhoc_svc.score(test_features, test_labels)

print(f"Callable kernel classification test score: {adhoc_score_callable_function}")

Callable kernel classification test score: 1.0

事前計算されたカーネル行列#

量子カーネルの関数を呼び出し可能として渡す代わりに、 scikit-learn SVC アルゴリズムに渡す前に、トレーニングとテストのカーネル行列を事前計算することもできます。

トレインとテスト行列を抽出するには、以前に定義したカーネルの evaluate を呼び出し、次のようにグラフィカルに視覚化します。

[7]:

adhoc_matrix_train = adhoc_kernel.evaluate(x_vec=train_features)
adhoc_matrix_test = adhoc_kernel.evaluate(x_vec=test_features, y_vec=train_features)

fig, axs = plt.subplots(1, 2, figsize=(10, 5))

axs[0].imshow(
    np.asmatrix(adhoc_matrix_train), interpolation="nearest", origin="upper", cmap="Blues"
)
axs[0].set_title("Ad hoc training kernel matrix")

axs[1].imshow(np.asmatrix(adhoc_matrix_test), interpolation="nearest", origin="upper", cmap="Reds")
axs[1].set_title("Ad hoc testing kernel matrix")

plt.show()

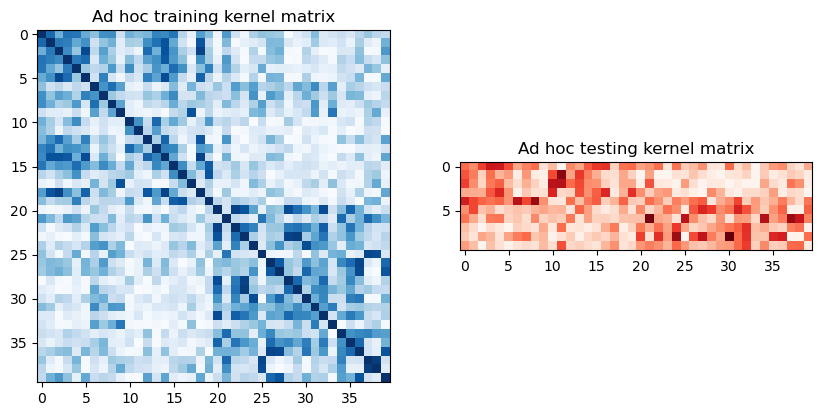
../_images/tutorials_03_quantum_kernel_17_0.png

これらの行列を使用するには、新しい SVC インスタンスの kernel パラメーターを "precomputed" に設定します。トレーニング行列とトレーニングデータセットを使用して fit を呼び出して分類器をトレーニングします。モデルがトレーニングされたら、テストデータセットのテスト行列を使用してモデルを評価します。

[8]:

adhoc_svc = SVC(kernel="precomputed")

adhoc_svc.fit(adhoc_matrix_train, train_labels)

adhoc_score_precomputed_kernel = adhoc_svc.score(adhoc_matrix_test, test_labels)

print(f"Precomputed kernel classification test score: {adhoc_score_precomputed_kernel}")

Precomputed kernel classification test score: 1.0

2.4. SVCによる分類#

QSVC は、便宜上 qiskit-machine-learning によって提供される代替トレーニングアルゴリズムです。これは、前に示した kernel.evaluate メソッドの代わりに量子カーネルを取り込む SVC の拡張機能です。

[9]:

from qiskit_machine_learning.algorithms import QSVC

qsvc = QSVC(quantum_kernel=adhoc_kernel)

qsvc.fit(train_features, train_labels)

qsvc_score = qsvc.score(test_features, test_labels)

print(f"QSVC classification test score: {qsvc_score}")

QSVC classification test score: 1.0

2.5. 分類に使用されるモデルの評価#

[10]:

print(f"Classification Model                    | Accuracy Score")
print(f"---------------------------------------------------------")
print(f"SVC using kernel as a callable function | {adhoc_score_callable_function:10.2f}")
print(f"SVC using precomputed kernel matrix     | {adhoc_score_precomputed_kernel:10.2f}")
print(f"QSVC                                    | {qsvc_score:10.2f}")

Classification Model                    | Accuracy Score
---------------------------------------------------------
SVC using kernel as a callable function |       1.00
SVC using precomputed kernel matrix     |       1.00
QSVC                                    |       1.00

分類データセットが小さいため、3つのモデルが100%の精度を達成していることがわかります。

3. クラスタリング#

このチュートリアルの 2 番目のワークフローは、qiskit-machine-learning を使用したクラスタリングタスクと、scikit-learn からのスペクトルクラスタリングアルゴリズムに焦点を当てています。

3.1. データセットの定義#

再び ad hoc dataset を使用しますが、2つのクラス間で 0.6 (以前の例では ``0.3` `) のギャップで生成されます。

クラスタリングは教師なし機械学習のカテゴリに属するため、テストデータセットは必要ありません。

[11]:

adhoc_dimension = 2
train_features, train_labels, test_features, test_labels, adhoc_total = ad_hoc_data(
    training_size=25,
    test_size=0,
    n=adhoc_dimension,
    gap=0.6,
    plot_data=False,
    one_hot=False,
    include_sample_total=True,
)

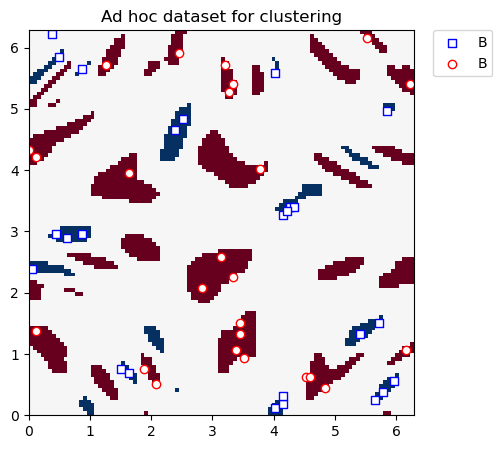
クラスタリングデータセットを以下にプロットします。

[12]:

plt.figure(figsize=(5, 5))
plt.ylim(0, 2 * np.pi)
plt.xlim(0, 2 * np.pi)
plt.imshow(
    np.asmatrix(adhoc_total).T,
    interpolation="nearest",
    origin="lower",
    cmap="RdBu",
    extent=[0, 2 * np.pi, 0, 2 * np.pi],
)

# A label plot
plot_features(plt, train_features, train_labels, 0, "s", "w", "b", "B")

# B label plot
plot_features(plt, train_features, train_labels, 1, "o", "w", "r", "B")

plt.legend(bbox_to_anchor=(1.05, 1), loc="upper left", borderaxespad=0.0)
plt.title("Ad hoc dataset for clustering")

plt.show()

../_images/tutorials_03_quantum_kernel_29_0.png

3.2. 量子カーネルの定義#

分類例と同じセットアップを使用します。 ZZFeatureMap を使用した FidelityQuantumKernel クラスの別のインスタンスを作成します。しかし、この場合、fidelity インスタンスは提供されません。これは、fidelityインスタンスが明示的に提供されていない場合、前のケースで提供されている``ComputeUncompute`` メソッドがデフォルトでインスタンス化されるためです。

[13]:

adhoc_feature_map = ZZFeatureMap(feature_dimension=adhoc_dimension, reps=2, entanglement="linear")

adhoc_kernel = FidelityQuantumKernel(feature_map=adhoc_feature_map)

3.3. スペクトルクラスタリングモデルとクラスタリング#

scikit-learn のスペクトルクラスタリング・アルゴリズムでは、 (SVC のように) 2つの方法でカスタムカーネルを定義することができます：

カーネルを 呼び出し可能な関数 として提供する
カーネル行列 を事前に計算する

qiskit-machine-learning の現在の FidelityQuantumKernel クラスでは、後者のオプションのみを使用できます。カーネル行列を事前に計算し、evaluate を呼び出し、次のように視覚化します。

[14]:

adhoc_matrix = adhoc_kernel.evaluate(x_vec=train_features)

plt.figure(figsize=(5, 5))
plt.imshow(np.asmatrix(adhoc_matrix), interpolation="nearest", origin="upper", cmap="Greens")
plt.title("Ad hoc clustering kernel matrix")
plt.show()

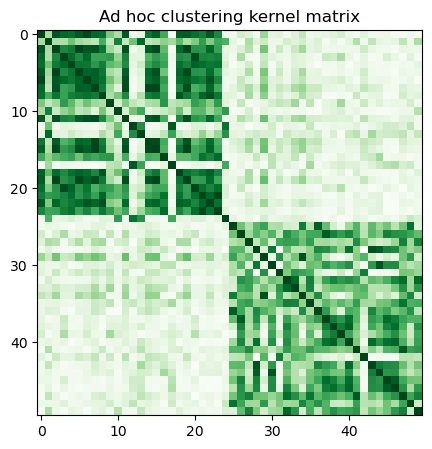
../_images/tutorials_03_quantum_kernel_33_0.png

次に、スペクトルクラスタリングモデルを定義し、あらかじめ計算されたカーネルを使用してそれを適合させます。さらに、正規化された相互情報を使ってラベルをスコアします。クラスのラベルはプリオリ(手前) であることが分かっています。

[15]:

from sklearn.cluster import SpectralClustering
from sklearn.metrics import normalized_mutual_info_score

adhoc_spectral = SpectralClustering(2, affinity="precomputed")

cluster_labels = adhoc_spectral.fit_predict(adhoc_matrix)

cluster_score = normalized_mutual_info_score(cluster_labels, train_labels)

print(f"Clustering score: {cluster_score}")

Clustering score: 0.7287008798015754

4. カーネル主成分解析#

このセクションでは、カーネルPCAアルゴリズムを使用した主成分分析タスクに焦点を当てます。 ZZFeatureMap を使用してカーネルマトリックスを計算し、このアプローチが元の機能を新しい空間に変換することを示します。軸を主成分に沿って選びます。この分野では、SVMではなく単純なモデルで分類作業を行うことができます。

4.1. データセットの定義#

2 つのクラス間の 0.6 のギャップを持つ ad hoc dataset を使用します。このデータセットは、クラスタリングセクションにあるデータセットに似ています。この場合、test_size はゼロではありません。

[16]:

adhoc_dimension = 2
train_features, train_labels, test_features, test_labels, adhoc_total = ad_hoc_data(
    training_size=25,
    test_size=10,
    n=adhoc_dimension,
    gap=0.6,
    plot_data=False,
    one_hot=False,
    include_sample_total=True,
)

トレーニングとテストのデータセットを以下に示します。このセクションの最終目標は、二つのクラスを直線的に分離できる新しい座標を構築することです。

[17]:

plot_dataset(train_features, train_labels, test_features, test_labels, adhoc_total)

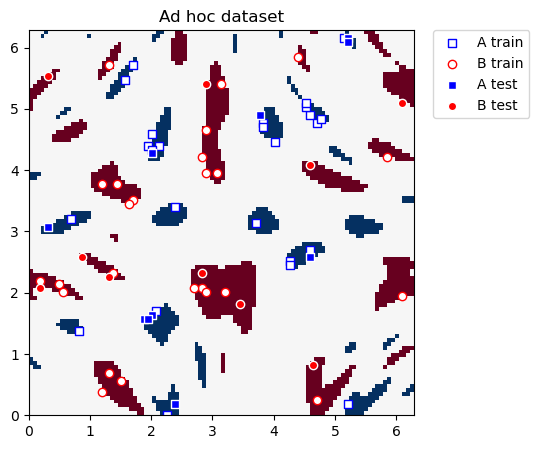
../_images/tutorials_03_quantum_kernel_40_0.png

4.2. 量子カーネルの定義#

分類作業と同じカーネルセットアップを進めます。つまり、特徴量マップとしての ZZFeatureMap 回路と、 FidelityQuantumKernel のインスタンスです。

[18]:

feature_map = ZZFeatureMap(feature_dimension=2, reps=2, entanglement="linear")
qpca_kernel = FidelityQuantumKernel(fidelity=fidelity, feature_map=feature_map)

次に、トレーニングとテスト機能のカーネル行列を評価します。

[19]:

matrix_train = qpca_kernel.evaluate(x_vec=train_features)
matrix_test = qpca_kernel.evaluate(x_vec=test_features, y_vec=train_features)

4.3. ガウシアンのカーネルPCAと量子カーネルの比較#

このセクションでは、scikit-learn から KernelPCA 実装を使用します。 gaussian カーネルの kernel パラメータを「rbf」に、量子カーネルの「precomputed」に設定します。前者は古典的な機械学習モデルで非常に人気がありますが、後者は qpca_kernel として定義された量子カーネルを使用できます。

ガウス系カーネルベースのKernel PCAモデルは、データセットを線形に分離可能にできず、量子カーネルは成功していることがわかります。

通常、PCAはデータセットの特徴量の数を減らすために使用されます。言い換えればデータセットの次元数を減らすために使われますが、ここではそのようには使いません。次元の数を保ち、カーネルPCAを使用するのは、主に可視化目的のためです。変換されたデータセットの分類がロジスティック回帰のような線形手法で容易に扱えることを示します。このメソッドを使用して、主要コンポーネント空間内の 2 つのクラスを scikit-learn の LogisticRegression モデルを使って分離します。いつものように、トレーニングデータセットに fit メソッドを呼び出し、モデルの正確性を score で評価することで訓練します。

[20]:

from sklearn.decomposition import KernelPCA

kernel_pca_rbf = KernelPCA(n_components=2, kernel="rbf")
kernel_pca_rbf.fit(train_features)
train_features_rbf = kernel_pca_rbf.transform(train_features)
test_features_rbf = kernel_pca_rbf.transform(test_features)

kernel_pca_q = KernelPCA(n_components=2, kernel="precomputed")
train_features_q = kernel_pca_q.fit_transform(matrix_train)
test_features_q = kernel_pca_q.transform(matrix_test)

モデルを訓練して得点をつけます。

[21]:

from sklearn.linear_model import LogisticRegression

logistic_regression = LogisticRegression()
logistic_regression.fit(train_features_q, train_labels)

logistic_score = logistic_regression.score(test_features_q, test_labels)
print(f"Logistic regression score: {logistic_score}")

Logistic regression score: 0.9

結果をプロットしてみましょう。まず、量子カーネルで得られる変換されたデータセットをプロットします。同じプロットでは、モデルの結果も追加します。そして、ガウスカーネルで得られる変換されたデータセットをプロットします。

[22]:

fig, (q_ax, rbf_ax) = plt.subplots(1, 2, figsize=(10, 5))


plot_features(q_ax, train_features_q, train_labels, 0, "s", "w", "b", "A train")
plot_features(q_ax, train_features_q, train_labels, 1, "o", "w", "r", "B train")

plot_features(q_ax, test_features_q, test_labels, 0, "s", "b", "w", "A test")
plot_features(q_ax, test_features_q, test_labels, 1, "o", "r", "w", "A test")

q_ax.set_ylabel("Principal component #1")
q_ax.set_xlabel("Principal component #0")
q_ax.set_title("Projection of training and test data\n using KPCA with Quantum Kernel")

# Plotting the linear separation
h = 0.01  # step size in the mesh

# create a mesh to plot in
x_min, x_max = train_features_q[:, 0].min() - 1, train_features_q[:, 0].max() + 1
y_min, y_max = train_features_q[:, 1].min() - 1, train_features_q[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

predictions = logistic_regression.predict(np.c_[xx.ravel(), yy.ravel()])

# Put the result into a color plot
predictions = predictions.reshape(xx.shape)
q_ax.contourf(xx, yy, predictions, cmap=plt.cm.RdBu, alpha=0.2)

plot_features(rbf_ax, train_features_rbf, train_labels, 0, "s", "w", "b", "A train")
plot_features(rbf_ax, train_features_rbf, train_labels, 1, "o", "w", "r", "B train")
plot_features(rbf_ax, test_features_rbf, test_labels, 0, "s", "b", "w", "A test")
plot_features(rbf_ax, test_features_rbf, test_labels, 1, "o", "r", "w", "A test")

rbf_ax.set_ylabel("Principal component #1")
rbf_ax.set_xlabel("Principal component #0")
rbf_ax.set_title("Projection of training data\n using KernelPCA")
plt.show()

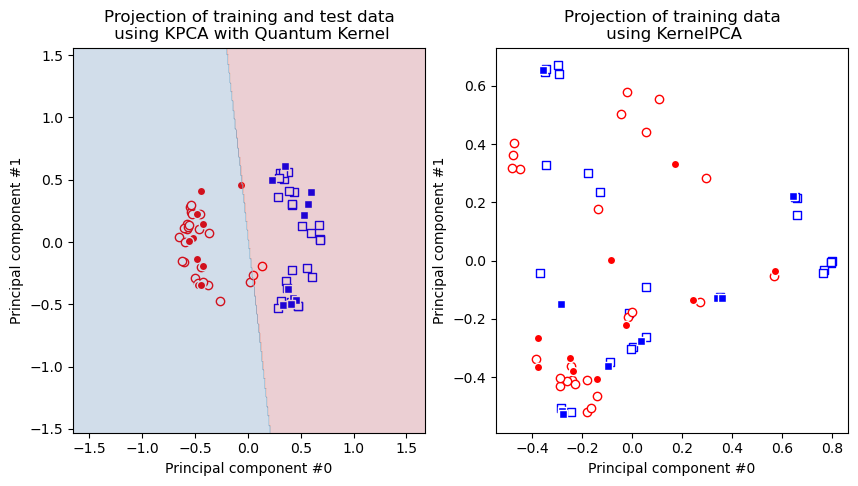
../_images/tutorials_03_quantum_kernel_50_0.png

ご覧のとおり、右の図のデータポイントは分離可能ではありませんが、左の図では分離可能です。したがって、量子カーネルの場合、変換されたデータセットに線形モデルを適用できます。これが、分類セクションで見た ad hoc データセットでSVM 分類器で分離可能である理由です。

5. 結論#

このチュートリアルでは:

量子カーネル学習の基礎をレビューしました
量子カーネルを FidelityQuantumKernel のインスタンスとして定義する方法を理解しました
カスタム量子カーネルを呼び出し可能な関数として使用する手法と、量子カーネル行列を事前計算する手法とで、 scikit-learn SVC アルゴリズムを使用して分類を行う方法を学びました
qiskit-machine-learning の QSVC アルゴリズムで分類器をトレーニングする方法を学びました
予め計算された量子カーネル行列で scikit-learn SpectralClustering アルゴリズムを使用してクラスタリングを行う方法を学びました
量子カーネルを scikit-learn の KernelPCA アルゴリズムに接続し、アドホックデータセットを線形モデルで取り組める新しいデータセットに変換する方法を調査しました

参考までに、 scikit-learn には、以下のような事前計算されたカーネル行列を使用できる他のアルゴリズムがあります。

[23]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
`qiskit-terra`	0.23.1
`qiskit-aer`	0.11.2
`qiskit-ibmq-provider`	0.20.0
`qiskit`	0.41.0
`qiskit-machine-learning`	0.5.0
System information
Python version	3.10.9
Python compiler	GCC 11.2.0
Python build	main, Jan 11 2023 15:21:40
OS	Linux
CPUs	10
Memory (Gb)	7.394691467285156
Wed Feb 22 10:36:16 2023 CET

This code is a part of Qiskit

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.