FineDrag¶

class FineDrag(physical_qubits, gate, backend=None)[source]¶

An experiment that performs fine characterizations of DRAG pulse coefficients.

Overview

FineDrag runs fine DRAG characterization experiments (see RoughDrag for the definition of DRAG pulses). Fine DRAG proceeds by iterating the gate sequence Rp - Rm where Rp is a rotation around an axis and Rm is the same rotation but in the opposite direction and is implemented by the gates Rz - Rp - Rz where the Rz gates are virtual Z-rotations, see Ref. [1]. The executed circuits are of the form

        ┌─────┐┌────┐┌───────┐┌────┐┌───────┐     ┌──────┐ ░ ┌─┐
   q_0: ┤ Pre ├┤ Rp ├┤ Rz(π) ├┤ Rp ├┤ Rz(π) ├ ... ┤ Post ├─░─┤M├
        └─────┘└────┘└───────┘└────┘└───────┘     └──────┘ ░ └╥┘
meas: 1/══════════════════════════════════════════════════════╩═
                                                              0

Here, “Pre” and “Post” designate gates that may be pre-appended and and post-appended, respectively, to the repeated sequence of Rp - Rz - Rp - Rz gates. When calibrating a pulse with a target rotation angle of π the Pre and Post gates are Id and RYGate(π/2), respectively. When calibrating a pulse with a target rotation angle of π/2 the Pre and Post gates are RXGate(π/2) and RYGate(π/2), respectively.

We now describe what this experiment corrects by following Ref. [2]. We follow equations 4.30 and onwards of Ref. [2] which state that the first-order corrections to the control fields are

\[\begin{split}\begin{align} \bar{\Omega}_x^{(1)}(t) = &\, 2\dot{s}^{(1)}_{x,0,1}(t) \\ \bar{\Omega}_y^{(1)}(t) = &\, 2\dot{s}^{(1)}_{y,0,1}(t) - s_{z,1}^{(1)}(t)t_g\Omega_x(t) \\ \bar{\delta}^{(1)}(t) = &\, \dot{s}_{z,1}^{(1)}(t) + 2s^{(1)}_{y,0,1}(t)t_g\Omega_x(t) + \frac{\lambda_1^2 t_g^2 \Omega_x^2(t)}{4} \end{align}\end{split}\]

Here, the \(s\) terms are coefficients of the expansion of an operator \(S(t)\) that generates a transformation that keeps the qubit sub-space isolated from the higher-order states. \(t_g\) is the gate time, \(\Omega_x(t)\) is the pulse envelope on the in-phase component of the drive and \(\lambda_1\) is a parameter of the Hamiltonian. For additional details please see Ref. [2]. As in Ref. [2] we now set \(s^{(1)}_{x,0,1}\) and \(s^{(1)}_{z,1}\) to zero and set \(s^{(1)}_{y,0,1}\) to \(-\lambda_1^2 t_g\Omega_x(t)/8\). This results in a Z angle rotation rate of \(\bar{\delta}^{(1)}(t)=0\) in the equations above and defines the value for the ideal \(\beta\) parameter. In Qiskit pulse, the definition of the DRAG pulse is

\[\Omega(t) = \Omega_x(t) + i\beta\,\dot{\Omega}_x(t)\quad\Longrightarrow\quad \Omega_y(t)= \beta\,\dot{\Omega}_x(t)\]

which implies that \(-\lambda_1^2 t_g/4\) is the ideal \(\beta\) value. We now assume that there is a small error \({\rm d}\beta\) in \(\beta\) such that the instantaneous Z-angle error induced by a single pulse is

\[\bar\delta(t) = {\rm d}\beta\, \Omega^2_x(t)\]

We can integrate \(\bar{\delta}(t)\), i.e. the instantaneous \(Z\)-angle rotation error, to obtain the total rotation angle error per pulse, \({\rm d}\theta\):

\[{\rm d}\theta = \int\bar\delta(t){\rm d}t = {\rm d}\beta \int\Omega^2_x(t){\rm d}t\]

If we assume a Gaussian pulse, i.e. \(\Omega_x(t)=A\exp[-t^2/(2\sigma^2)]\) then the integral of \(\Omega_x^2(t)\) in the equation above results in \(A^2\sigma\sqrt{\pi}\). Furthermore, the integral of \(\Omega_x(t)\) is \(A\sigma\sqrt{\pi/2}=\theta_\text{target}\), where \(\theta_\text{target}\) is the target rotation angle, i.e. the area under the pulse. This last point allows us to rewrite \(A^2\sigma\sqrt{\pi}\) as \(\theta^2_\text{target}/(2\sigma\sqrt{\pi})\). The total \(Z\) angle error per pulse is therefore

\[{\rm d}\theta= \int\bar\delta(t){\rm d}t={\rm d}\beta\,\frac{\theta^2_\text{target}}{2\sigma\sqrt{\pi}}\]

Here, \({\rm d}\theta\) is the \(Z\) angle error per pulse. The qubit population produced by the gate sequence shown above is used to measure \({\rm d}\theta\). Indeed, each gate pair Rp - Rm will produce a small unwanted \(Z\)-rotation out of the \(ZX\) plane with a magnitude \(2\,{\rm d}\theta\). The total rotation out of the \(ZX\) plane is then mapped to a qubit population by the final Post gate. Inverting the relation above after cancelling out the factor of two due to the Rp - Rm pulse pair yields the error in \(\beta\) that produced the rotation error \({\rm d}\theta\) as

\[{\rm d}\beta=\frac{\sqrt{\pi}\,{\rm d}\theta\sigma}{ \theta_\text{target}^2}.\]

This is the correction formula in the FineDRAG Updater.

References

[1] David C. McKay, Christopher J. Wood, Sarah Sheldon, Jerry M. Chow, Jay M. Gambetta, Efficient Z-Gates for Quantum Computing, Phys. Rev. A 96, 022330 (2017), doi: 10.1103/PhysRevA.96.022330 (open)

[2] J. M. Gambetta, F. Motzoi, S. T. Merkel, F. K. Wilhelm, Analytic control methods for high fidelity unitary operations in a weakly nonlinear oscillator, Phys. Rev. A 83, 012308 (2011), doi: 10.1103/PhysRevA.83.012308 (open)

Analysis class reference

ErrorAmplificationAnalysis

Experiment options

These options can be set by the set_experiment_options() method.

Options

Defined in the class FineDrag:
- repetitions (List[int])
  
  Default value: [0, 1, 2, 3, 4, …]
  
  A list of the number of times that Rp - Rm gate sequence is repeated.
- gate (Gate)
  
  Default value: None
  
  This is the gate such as XGate() that will be in the circuits.
Defined in the class BaseExperiment:
- max_circuits (Optional[int])
  
  Default value: None
  
  The maximum number of circuits per job when running an experiment on a backend.

Example

from qiskit.circuit.library import XGate
from qiskit_experiments.library.characterization import FineDrag

exp = FineDrag(physical_qubits=(0,), gate=XGate(), backend=backend)

exp_data = exp.run().block_for_results()
display(exp_data.figure(0))
exp_data.analysis_results(dataframe=True)

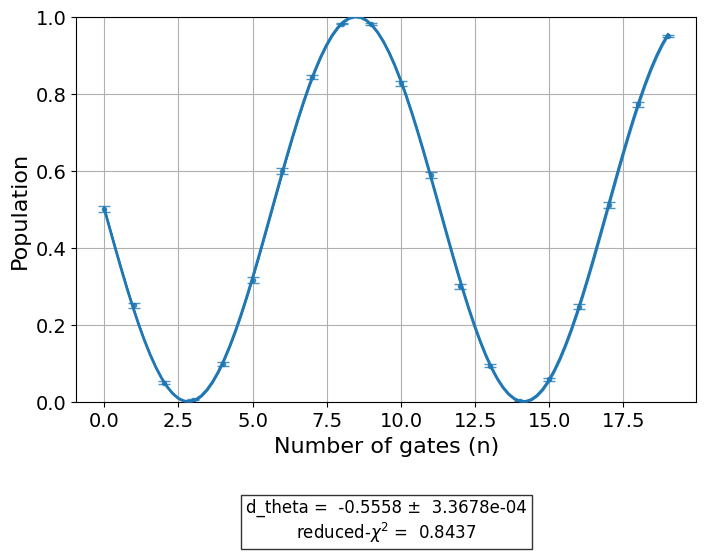
../_images/qiskit_experiments.library.characterization.FineDrag_1_0.png

	name	experiment	components	value	quality	backend	run_time	chisq
aa7728d6	d_theta	FineDrag	[Q0]	0.0092+/-0.0012	good	aer_simulator	None	0.523434

Initialization

Setup a fine amplitude experiment on the given qubit.

Parameters:

physical_qubits (Sequence[int]) – List containing the qubit on which to run the fine amplitude calibration experiment.
gate (Gate) – The gate that will be repeated.
backend (Backend | None) – Optional, the backend to run the experiment on.

Attributes

analysis¶: Return the analysis instance for the experiment

backend¶: Return the backend for the experiment

experiment_options¶: Return the options for the experiment.

experiment_type¶: Return experiment type.

num_qubits¶: Return the number of qubits for the experiment.

physical_qubits¶: Return the device qubits for the experiment.

run_options¶: Return options values for the experiment run() method.

transpile_options¶: Return the transpiler options for the run() method.

Methods

circuits()[source]¶

Create the circuits for the fine DRAG calibration experiment.

Returns:: A list of circuits with a variable number of gates.
Return type:: List[QuantumCircuit]

config()¶

Return the config dataclass for this experiment

Return type:: ExperimentConfig

copy()¶

Return a copy of the experiment

Return type:: BaseExperiment

classmethod from_config(config)¶

Initialize an experiment from experiment config

Return type:: BaseExperiment

job_info(backend=None)¶

Get information about job distribution for the experiment on a specific backend.

Parameters:

backend (Backend) – Optional, the backend for which to get job distribution information. If not specified, the experiment must already have a set backend.

Returns:

A dictionary containing information about job distribution.

”Total number of circuits in the experiment”: Total number of circuits in the experiment.

”Maximum number of circuits per job”: Maximum number of circuits in one job based on backend and experiment settings.

”Total number of jobs”: Number of jobs needed to run this experiment on the currently set backend.

Return type:

dict

Raises:

QiskitError – if backend is not specified.

run(backend=None, sampler=None, analysis='default', timeout=None, backend_run=None, **run_options)¶

Run an experiment and perform analysis.

Parameters:

backend (Backend | None) – Optional, the backend to run on. Will override existing backend settings.
sampler (BaseSamplerV2 | None) – Optional, the sampler to run the experiment on. If None then a sampler will be invoked from previously set backend
analysis (BaseAnalysis | None) – Optional, a custom analysis instance to use for performing analysis. If None analysis will not be run. If "default" the experiments analysis() instance will be used if it contains one.
timeout (float | None) – Time to wait for experiment jobs to finish running before cancelling.
backend_run (bool | None) – Use backend run (temp option for testing)
run_options – backend runtime options used for circuit execution.

Returns:

The experiment data object.

Raises:

QiskitError – If experiment is run with an incompatible existing ExperimentData container.

Return type:

ExperimentData

set_experiment_options(**fields)¶

Set the experiment options.

Parameters:: fields – The fields to update the options
Raises:: AttributeError – If the field passed in is not a supported options

set_run_options(**fields)¶

Set options values for the experiment run() method.

Parameters:: fields – The fields to update the options