Quantum State Tomography

Quantum tomography is an experimental procedure to reconstruct a description of part of a quantum system from the measurement outcomes of a specific set of experiments. In particular, quantum state tomography reconstructs the density matrix of a quantum state by preparing the state many times and measuring them in a tomographically complete basis of measurement operators.

Note

This tutorial requires the qiskit-aer and qiskit-ibm-runtime packages to run simulations. You can install them with python -m pip install qiskit-aer qiskit-ibm-runtime.

We first initialize a simulator to run the experiments on.

from qiskit_aer import AerSimulator
from qiskit_ibm_runtime.fake_provider import FakePerth

backend = AerSimulator.from_backend(FakePerth())

To run a state tomography experiment, we initialize the experiment with a circuit to prepare the state to be measured. We can also pass in an Operator or a Statevector to describe the preparation circuit.

import qiskit
from qiskit_experiments.framework import ParallelExperiment
from qiskit_experiments.library import StateTomography

# GHZ State preparation circuit
nq = 2
qc_ghz = qiskit.QuantumCircuit(nq)
qc_ghz.h(0)
qc_ghz.s(0)
for i in range(1, nq):
    qc_ghz.cx(0, i)

# QST Experiment
qstexp1 = StateTomography(qc_ghz)
qstdata1 = qstexp1.run(backend, seed_simulation=100).block_for_results()

# Print results
display(qstdata1.analysis_results(dataframe=True))
name experiment components value quality backend run_time trace eigvals raw_eigvals rescaled_psd fitter_metadata conditional_probability positive
152f802d state StateTomography [Q0, Q1] DensityMatrix([[ 0.47477214+0.j , 0.00... None aer_simulator_from(fake_perth) None 1.0 [0.9161183509870341, 0.04749004975662149, 0.02... [0.9161183509870341, 0.04749004975662149, 0.02... False {'fitter': 'linear_inversion', 'fitter_time': ... 1.0 True
c310f8e2 state_fidelity StateTomography [Q0, Q1] 0.914551 None aer_simulator_from(fake_perth) None None None None None None None None
ad1fc9d9 positive StateTomography [Q0, Q1] True None aer_simulator_from(fake_perth) None None None None None None None None

Tomography Results

The main result for tomography is the fitted state, which is stored as a DensityMatrix object:

state_result = qstdata1.analysis_results("state", dataframe=True).iloc[0]
print(state_result.value)

DensityMatrix([[ 0.47477214+0.j        ,  0.00683594-0.01611328j,
                 0.00651042+0.02132161j, -0.00732422-0.44726562j],
               [ 0.00683594+0.01611328j,  0.02750651+0.j        ,
                 0.01220703-0.00195312j,  0.00651042-0.00309245j],
               [ 0.00651042-0.02132161j,  0.01220703+0.00195312j,
                 0.03792318+0.j        , -0.02246094+0.00048828j],
               [-0.00732422+0.44726562j,  0.00651042+0.00309245j,
                -0.02246094-0.00048828j,  0.45979818+0.j        ]],
              dims=(2, 2))

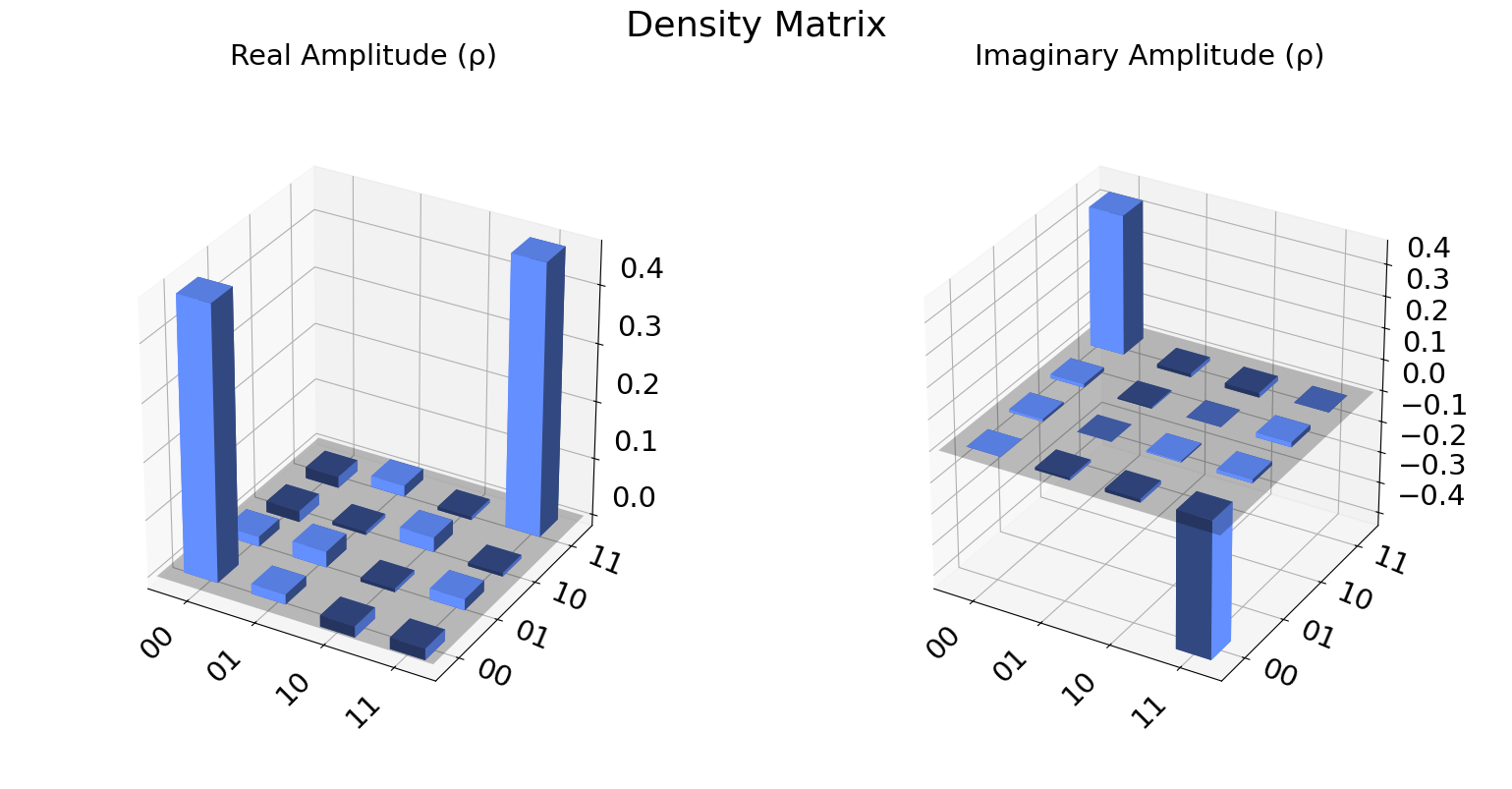
We can also visualize the density matrix:

from qiskit.visualization import plot_state_city
state = qstdata1.analysis_results("state", dataframe=True).iloc[0].value
plot_state_city(state, title='Density Matrix')
../../_images/state_tomography_3_0.png

The state fidelity of the fitted state with the ideal state prepared by the input circuit is stored in the "state_fidelity" result field. Note that if the input circuit contained any measurements the ideal state cannot be automatically generated and this field will be set to None.

fid_result = qstdata1.analysis_results("state_fidelity", dataframe=True).iloc[0]
print("State Fidelity = {:.5f}".format(fid_result.value))

State Fidelity = 0.91455

Additional state metadata

Additional data is stored in the tomography under additional fields. This includes

  • eigvals: the eigenvalues of the fitted state

  • trace: the trace of the fitted state

  • positive: Whether the eigenvalues are all non-negative

If trace rescaling was performed this dictionary will also contain a raw_trace field containing the trace before rescaling. Futhermore, if the state was rescaled to be positive or trace 1 an additional field raw_eigvals will contain the state eigenvalues before rescaling was performed.

for col in ["eigvals", "trace", "positive"]:
    print(f"{col}: {state_result[col]}")

eigvals: [0.91611835 0.04749005 0.02336872 0.01302288]
trace: 1.0000000000000016
positive: True

To see the effect of rescaling, we can perform a “bad” fit with very low counts:

# QST Experiment
bad_data = qstexp1.run(backend, shots=10, seed_simulation=100).block_for_results()
bad_state_result = bad_data.analysis_results("state", dataframe=True).iloc[0]

# Print result
for key, val in bad_state_result.items():
    print(f"{key}: {val}")

name: state
experiment: StateTomography
components: [<Qubit(Q0)>, <Qubit(Q1)>]
value: DensityMatrix([[ 0.44821797+0.00000000e+00j, -0.09640526-1.51481655e-01j,
                 0.00203485-5.31097116e-02j, -0.01100238-3.88870802e-01j],
               [-0.09640526+1.51481655e-01j,  0.11305966+1.73472348e-18j,
                 0.03602698-1.79217234e-02j,  0.15538061+3.31586074e-02j],
               [ 0.00203485+5.31097116e-02j,  0.03602698+1.79217234e-02j,
                 0.03656753+0.00000000e+00j,  0.08989397-8.35621624e-03j],
               [-0.01100238+3.88870802e-01j,  0.15538061-3.31586074e-02j,
                 0.08989397+8.35621624e-03j,  0.40215484+0.00000000e+00j]],
              dims=(2, 2))
quality: None
backend: aer_simulator_from(fake_perth)
run_time: None
trace: 1.0000000000000002
eigvals: [0.89974152 0.10025848 0.         0.        ]
raw_eigvals: [ 0.99273195  0.19324891 -0.0052429  -0.18073796]
rescaled_psd: True
fitter_metadata: {'fitter': 'linear_inversion', 'fitter_time': 0.0036444664001464844}
conditional_probability: 1.0
positive: True

Tomography Fitters

The default fitters is linear_inversion, which reconstructs the state using dual basis of the tomography basis. This will typically result in a non-positive reconstructed state. This state is rescaled to be positive-semidefinite (PSD) by computing its eigen-decomposition and rescaling its eigenvalues using the approach from Ref. [1].

There are several other fitters are included (See API documentation for details). For example, if cvxpy is installed we can use the cvxpy_gaussian_lstsq() fitter, which allows constraining the fit to be PSD without requiring rescaling.

try:
    import cvxpy

    # Set analysis option for cvxpy fitter
    qstexp1.analysis.set_options(fitter='cvxpy_gaussian_lstsq')

    # Re-run experiment
    qstdata2 = qstexp1.run(backend, seed_simulation=100).block_for_results()

    state_result2 = qstdata2.analysis_results("state", dataframe=True).iloc[0]
    for key, val in state_result2.items():
        print(f"{key}: {val}")

except ModuleNotFoundError:
    print("CVXPY is not installed")

name: state
experiment: StateTomography
components: [<Qubit(Q0)>, <Qubit(Q1)>]
value: DensityMatrix([[ 0.45923303+0.j        , -0.0045762 +0.00134729j,
                -0.00565893-0.009983j  , -0.00595507-0.43820044j],
               [-0.0045762 -0.00134729j,  0.02996372+0.j        ,
                -0.01280257+0.00527123j,  0.00645056+0.00853883j],
               [-0.00565893+0.009983j  , -0.01280257-0.00527123j,
                 0.03855425+0.j        , -0.00693283-0.00908521j],
               [-0.00595507+0.43820044j,  0.00645056-0.00853883j,
                -0.00693283+0.00908521j,  0.472249  +0.j        ]],
              dims=(2, 2))
quality: None
backend: aer_simulator_from(fake_perth)
run_time: None
trace: 0.9999999976684613
eigvals: [0.90415892 0.05767847 0.02312496 0.01503765]
raw_eigvals: [0.90415892 0.05767847 0.02312496 0.01503765]
rescaled_psd: False
fitter_metadata: {'fitter': 'cvxpy_gaussian_lstsq', 'cvxpy_solver': 'SCS', 'cvxpy_status': ['optimal'], 'psd_constraint': True, 'trace_preserving': True, 'fitter_time': 0.031495094299316406}
conditional_probability: 1.0
positive: True

Parallel Tomography Experiment

We can also use the ParallelExperiment class to run subsystem tomography on multiple qubits in parallel.

For example if we want to perform 1-qubit QST on several qubits at once:

from math import pi
num_qubits = 5
gates = [qiskit.circuit.library.RXGate(i * pi / (num_qubits - 1))
         for i in range(num_qubits)]

subexps = [
    StateTomography(gate, physical_qubits=(i,))
    for i, gate in enumerate(gates)
]
parexp = ParallelExperiment(subexps)
pardata = parexp.run(backend, seed_simulation=100).block_for_results()

display(pardata.analysis_results(dataframe=True))
name experiment components value quality backend run_time trace eigvals raw_eigvals rescaled_psd fitter_metadata conditional_probability positive
18635584 state StateTomography [Q0] DensityMatrix([[0.9765625 +0.j , 0.0107... None aer_simulator_from(fake_perth) None 1.0 [0.9767325676309926, 0.02326743236900829] [0.9767325676309926, 0.02326743236900829] False {'fitter': 'linear_inversion', 'fitter_time': ... 1.0 True
8daa7697 state_fidelity StateTomography [Q0] 0.976562 None aer_simulator_from(fake_perth) None None None None None None None None
0baaad87 positive StateTomography [Q0] True None aer_simulator_from(fake_perth) None None None None None None None None
b7ad7565 state StateTomography [Q1] DensityMatrix([[0.828125 +0.j , 0.00781... None aer_simulator_from(fake_perth) None 1.0 [0.9781128725994654, 0.021887127400535417] [0.9781128725994654, 0.021887127400535417] False {'fitter': 'linear_inversion', 'fitter_time': ... 1.0 True
7eacf0e5 state_fidelity StateTomography [Q1] 0.97785 None aer_simulator_from(fake_perth) None None None None None None None None
8f5c964d positive StateTomography [Q1] True None aer_simulator_from(fake_perth) None None None None None None None None
9797128a state StateTomography [Q2] DensityMatrix([[ 0.50097656+0.j , -0.00... None aer_simulator_from(fake_perth) None 1.0 [0.9697438195244785, 0.030256180475522476] [0.9697438195244785, 0.030256180475522476] False {'fitter': 'linear_inversion', 'fitter_time': ... 1.0 True
bb73cadf state_fidelity StateTomography [Q2] 0.969727 None aer_simulator_from(fake_perth) None None None None None None None None
1e5e5531 positive StateTomography [Q2] True None aer_simulator_from(fake_perth) None None None None None None None None
54ee8a13 state StateTomography [Q3] DensityMatrix([[0.16601563+0.j , 0.0136... None aer_simulator_from(fake_perth) None 1.0 [0.9569237737544116, 0.04307622624558921] [0.9569237737544116, 0.04307622624558921] False {'fitter': 'linear_inversion', 'fitter_time': ... 1.0 True
b29d408f state_fidelity StateTomography [Q3] 0.956443 None aer_simulator_from(fake_perth) None None None None None None None None
5ca6013e positive StateTomography [Q3] True None aer_simulator_from(fake_perth) None None None None None None None None
c68a4792 state StateTomography [Q4] DensityMatrix([[ 0.02929688+0.j , -0.01... None aer_simulator_from(fake_perth) None 1.0 [0.9709968125545261, 0.02900318744547488] [0.9709968125545261, 0.02900318744547488] False {'fitter': 'linear_inversion', 'fitter_time': ... 1.0 True
c29bbec1 state_fidelity StateTomography [Q4] 0.970703 None aer_simulator_from(fake_perth) None None None None None None None None
2606aa3d positive StateTomography [Q4] True None aer_simulator_from(fake_perth) None None None None None None None None

View experiment analysis results for one component:

results = pardata.analysis_results(dataframe=True)
display(results[results.components.apply(lambda x: x == ["Q0"])])
name experiment components value quality backend run_time trace eigvals raw_eigvals rescaled_psd fitter_metadata conditional_probability positive
18635584 state StateTomography [Q0] DensityMatrix([[0.9765625 +0.j , 0.0107... None aer_simulator_from(fake_perth) None 1.0 [0.9767325676309926, 0.02326743236900829] [0.9767325676309926, 0.02326743236900829] False {'fitter': 'linear_inversion', 'fitter_time': ... 1.0 True
8daa7697 state_fidelity StateTomography [Q0] 0.976562 None aer_simulator_from(fake_perth) None None None None None None None None
0baaad87 positive StateTomography [Q0] True None aer_simulator_from(fake_perth) None None None None None None None None

References

See also