ZZRamsey¶
- class ZZRamsey(physical_qubits, backend=None, **experiment_options)[source]¶
An experiment to characterize the static \(ZZ\) interaction for a qubit pair.
Overview
This experiment assumes a two qubit Hamiltonian of the form
\[H = h \left(\frac{f_0}{2} ZI + \frac{f_1}{2} IZ + \frac{f_{ZZ}}{4} ZZ\right)\]and measures the strength \(f_{ZZ}\) of the \(ZZ\) term. \(f_{ZZ}\) can be described as the difference between the frequency of qubit 0 when qubit 1 is excited and the frequency of qubit 0 when qubit 1 is in the ground state. Because \(f_{ZZ}\) is symmetric in qubit index, it can also be expressed with the roles of 0 and 1 reversed. Experimentally, we measure \(f_{ZZ}\) by performing Ramsey sequences on qubit 0 with qubit 1 in the ground state and again with qubit 1 in the excited state. The standard Ramsey experiment consists of putting a qubit along the \(X\) axis of Bloch sphere, waiting for some time, and then measuring the qubit project along \(X\). By measuring the \(X\) projection versus time the qubit frequency can be inferred. See
T2RamseyandRamseyXY.Because we are interested in the difference in qubit 0 frequency between the two qubit 1 preparations rather than the absolute frequencies of qubit 0 for those preparations, we modify the Ramsey sequences (the circuits for the modified sequences are shown below). First, we add an X gate on qubit 0 to the middle of the Ramsey delay. This would have the effect of echoing out the phase accumulation of qubit 0 (like a Hahn echo sequence as used in
T2Hahn), but we add a simultaneous X gate to qubit 1 as well. Flipping qubit 1 inverts the sign of the \(f_{ZZ}\) term. The net result is that qubit 0 continues to accumulate phase proportional to \(f_{ZZ}\) while the phase due to any ZI term is canceled out. This technique allows \(f_{ZZ}\) to be measured using longer delay times than might otherwise be possible with a qubit with a slow frequency drift (i.e. the measurement is not sensitive to qubit frequency drift from shot to shot, only to drift within a single shot).The resulting excited state population of qubit 0 versus delay time exhibits slow sinusoidal oscillations (assuming \(f_{ZZ}\) is relatively small). To help with distinguishing between qubit decay and a slow oscillation, an extra Z rotation is applied before the final pulse on qubit 0. The angle of this Z rotation is set proportional to the delay time of the sequence. This angle proportional to time behaves similarly to measuring at a fixed angle with the qubit rotating at a constant frequency. This virtual frequency is common to the two qubit 1 preparations. By looking at the difference in frequency fitted for the two cases, this virtual frequency (called \(f\) in the circuits shown below) is removed, leaving only the \(f_{ZZ}\) value. The value of \(f\) in terms of the experiment options is
num_rotations / (max(delays) - min(delays)).This experiment consists of the following two circuits repeated with different
delayvalues.Modified Ramsey sequence with qubit 1 initially in the ground state ┌────┐ ░ ┌─────────────────┐ ░ ┌───┐ ░ ┌─────────────────┐ ░ » q_0: ┤ √X ├─░─┤ Delay(delay[s]) ├─░─┤ X ├─░─┤ Delay(delay[s]) ├─░─» └────┘ ░ └─────────────────┘ ░ ├───┤ ░ └─────────────────┘ ░ » q_1: ───────░─────────────────────░─┤ X ├─░─────────────────────░─» ░ ░ └───┘ ░ ░ » c: 1/═════════════════════════════════════════════════════════════» » « ┌─────────────────────┐┌────┐ ░ ┌─┐ «q_0: ┤ Rz(4*delay*dt*f*pi) ├┤ √X ├─░─┤M├ « └────────┬───┬────────┘└────┘ ░ └╥┘ «q_1: ─────────┤ X ├────────────────░──╫─ « └───┘ ░ ║ «c: 1/═════════════════════════════════╩═ « 0 Modified Ramsey sequence with qubit 1 initially in the excited state ┌────┐ ░ ┌─────────────────┐ ░ ┌───┐ ░ ┌─────────────────┐ ░ » q_0: ┤ √X ├─░─┤ Delay(delay[s]) ├─░─┤ X ├─░─┤ Delay(delay[s]) ├─░─» ├───┬┘ ░ └─────────────────┘ ░ ├───┤ ░ └─────────────────┘ ░ » q_1: ┤ X ├──░─────────────────────░─┤ X ├─░─────────────────────░─» └───┘ ░ ░ └───┘ ░ ░ » c: 1/═════════════════════════════════════════════════════════════» » « ┌─────────────────────┐┌────┐ ░ ┌─┐ «q_0: ┤ Rz(4*delay*dt*f*pi) ├┤ √X ├─░─┤M├ « └─────────────────────┘└────┘ ░ └╥┘ «q_1: ──────────────────────────────░──╫─ « ░ ║ «c: 1/═════════════════════════════════╩═ « 0Analysis class reference
Experiment options
These options can be set by the
set_experiment_options()method.- Options
Defined in the class
ZZRamsey:delays (list[float])
Default value:NoneThe list of delays that will be scanned in the experiment, in seconds. If not set, thennum_delaysevenly spaced delays betweenmin_delayandmax_delayare used. Ifdelaysis set,max_delay,min_delay, andnum_delaysare ignored.max_delay (float)
Default value:1e-05Maximum delay time to use.min_delay (float)
Default value:0.0Minimum delay time to use.num_delays (int)
Default value:50Number of circuits to use per control state preparation.num_rotations (float)
Default value:5The extra rotation added to qubit 0 uses a frequency that gives this many rotations in the case where \(f_{ZZ}\) is 0.
Defined in the class
BaseExperiment:max_circuits (Optional[int])
Default value:NoneThe maximum number of circuits per job when running an experiment on a backend.
Example
from qiskit_experiments.library.characterization import ZZRamsey exp = ZZRamsey(physical_qubits=(0,1), backend=backend) exp_data = exp.run().block_for_results() display(exp_data.figure(0)) exp_data.analysis_results(dataframe=True)
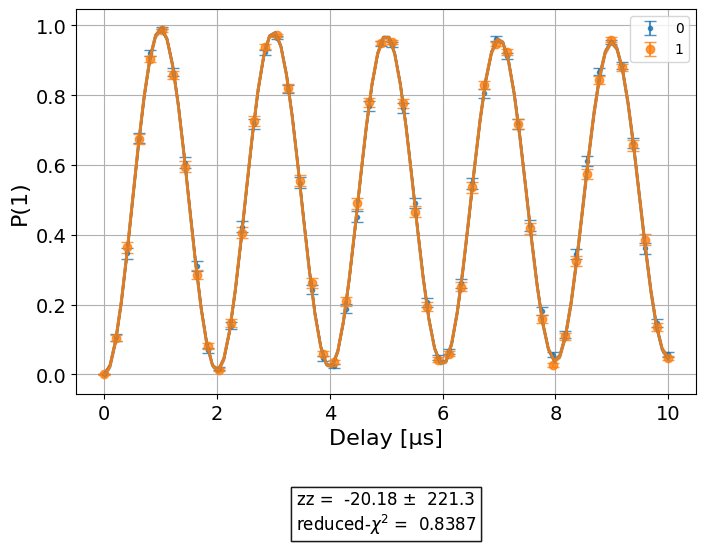
name experiment components value quality backend run_time chisq 5f0cf71e zz ZZRamsey [Q0, Q1] (4.986+/-0.018)e+04 good ZZRamsey_simulator None 7.900207 Initialization
Create new experiment.
- Parameters:
physical_qubits (Tuple[int, int]) – The qubits on which to run the Ramsey XY experiment.
backend (Backend | None) – Optional, the backend to run the experiment on.
experiment_options – experiment options to set
Attributes
- analysis¶
Return the analysis instance for the experiment
- backend¶
Return the backend for the experiment
- experiment_options¶
Return the options for the experiment.
- experiment_type¶
Return experiment type.
- num_qubits¶
Return the number of qubits for the experiment.
- physical_qubits¶
Return the device qubits for the experiment.
Methods
- circuits()[source]¶
Create circuits
- Returns:
A list of circuits with a variable delay.
- Return type:
List[QuantumCircuit]
- config()¶
Return the config dataclass for this experiment
- Return type:
- copy()¶
Return a copy of the experiment
- Return type:
- delays()[source]¶
Delay values to use in circuits
- Returns:
The list of delays to use for the different circuits based on the experiment options.
- Return type:
List[float]
- frequency()[source]¶
Frequency of qubit rotation when ZZ is 0
This method calculates the simulated frequency applied to both sets of circuits. The value is chosen to induce num_rotations number of rotation within the time window that the delay is swept through.
- Returns:
The frequency at which the target qubit will rotate when ZZ is zero based on the current experiment options.
- Return type:
float
- classmethod from_config(config)¶
Initialize an experiment from experiment config
- Return type:
- job_info(backend=None)¶
Get information about job distribution for the experiment on a specific backend.
- Parameters:
backend (Backend) – Optional, the backend for which to get job distribution information. If not specified, the experiment must already have a set backend.
- Returns:
A dictionary containing information about job distribution.
”Total number of circuits in the experiment”: Total number of circuits in the experiment.
”Maximum number of circuits per job”: Maximum number of circuits in one job based on backend and experiment settings.
”Total number of jobs”: Number of jobs needed to run this experiment on the currently set backend.
- Return type:
dict
- Raises:
QiskitError – if backend is not specified.
- parametrized_circuits()[source]¶
Create circuits with parameters for numerical quantities
This method is primarily intended for generating template circuits that visualize well. It inserts
qiskit.circuit.Parameters for \(π\) and dt as well the target qubit rotation frequency f.- Returns:
Parameterized circuits for the case of the control qubit being in 0 and in 1.
- Return type:
Tuple[QuantumCircuit, QuantumCircuit]
- run(backend=None, sampler=None, analysis='default', timeout=None, backend_run=None, **run_options)¶
Run an experiment and perform analysis.
- Parameters:
backend (Backend | None) – Optional, the backend to run on. Will override existing backend settings.
sampler (BaseSamplerV2 | None) – Optional, the sampler to run the experiment on. If None then a sampler will be invoked from previously set backend
analysis (BaseAnalysis | None) – Optional, a custom analysis instance to use for performing analysis. If None analysis will not be run. If
"default"the experimentsanalysis()instance will be used if it contains one.timeout (float | None) – Time to wait for experiment jobs to finish running before cancelling.
backend_run (bool | None) – Use backend run (temp option for testing)
run_options – backend runtime options used for circuit execution.
- Returns:
The experiment data object.
- Raises:
QiskitError – If experiment is run with an incompatible existing ExperimentData container.
- Return type:
- set_experiment_options(**fields)¶
Set the experiment options.
- Parameters:
fields – The fields to update the options
- Raises:
AttributeError – If the field passed in is not a supported options
- set_run_options(**fields)¶
Set options values for the experiment
run()method.- Parameters:
fields – The fields to update the options
See also
The Setting options for your experiment guide for code example.
- set_transpile_options(**fields)¶
Set the transpiler options for
run()method.- Parameters:
fields – The fields to update the options
- Raises:
QiskitError – If initial_layout is one of the fields.
See also
The Setting options for your experiment guide for code example.