Nota
Esta página fue generada a partir de docs/tutorials/08_quantum_kernel_trainer.ipynb.
Entrenamiento de Kernel Cuántico para Aplicaciones de Machine Learning#
En este tutorial, entrenaremos un kernel cuántico sobre un conjunto de datos etiquetado para una aplicación de machine learning. Para ilustrar los pasos básicos, usaremos la Alineación de Kernel Cuántico (Quantum Kernel Alignment, QKA) para una tarea de clasificación binaria. QKA es una técnica que adapta iterativamente un kernel cuántico parametrizado a un conjunto de datos mientras converge al margen máximo de SVM. Se puede encontrar más información sobre QKA en la preimpresión, «Covariant quantum kernels for data with group structure.»
El punto de entrada para entrenar un kernel cuántico es la clase QuantumKernelTrainer. Los pasos básicos son:
Preparar el conjunto de datos
Definir el mapa cuántico de características
Configurar una instancia de los objetos
TrainableKernelyQuantumKernelTrainerUtilizar el método
QuantumKernelTrainer.fitpara entrenar los parámetros del kernel sobre el conjunto de datosPasar el kernel cuántico entrenado a un modelo de machine learning
Importar Paquetes Locales, Externos y de Qiskit y definir una clase de devolución de llamada (callback) para nuestro optimizador#
[1]:
# External imports
from pylab import cm
from sklearn import metrics
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# Qiskit imports
from qiskit import QuantumCircuit
from qiskit.circuit import ParameterVector
from qiskit.visualization import circuit_drawer
from qiskit.circuit.library import ZZFeatureMap
from qiskit_algorithms.optimizers import SPSA
from qiskit_machine_learning.kernels import TrainableFidelityQuantumKernel
from qiskit_machine_learning.kernels.algorithms import QuantumKernelTrainer
from qiskit_machine_learning.algorithms import QSVC
from qiskit_machine_learning.datasets import ad_hoc_data
class QKTCallback:
"""Callback wrapper class."""
def __init__(self) -> None:
self._data = [[] for i in range(5)]
def callback(self, x0, x1=None, x2=None, x3=None, x4=None):
"""
Args:
x0: number of function evaluations
x1: the parameters
x2: the function value
x3: the stepsize
x4: whether the step was accepted
"""
self._data[0].append(x0)
self._data[1].append(x1)
self._data[2].append(x2)
self._data[3].append(x3)
self._data[4].append(x4)
def get_callback_data(self):
return self._data
def clear_callback_data(self):
self._data = [[] for i in range(5)]
Preparar el Conjunto de Datos#
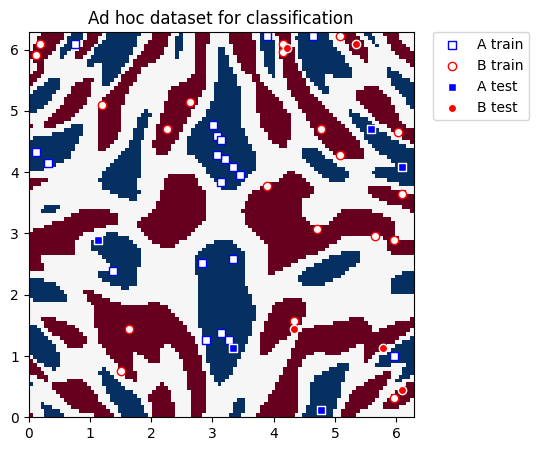
En esta guía, utilizaremos el conjunto de datos ad_hoc.py de Qiskit Machine Learning para demostrar el proceso de entrenamiento del kernel. Consulta la documentación aquí.
[2]:
adhoc_dimension = 2
X_train, y_train, X_test, y_test, adhoc_total = ad_hoc_data(
training_size=20,
test_size=5,
n=adhoc_dimension,
gap=0.3,
plot_data=False,
one_hot=False,
include_sample_total=True,
)
plt.figure(figsize=(5, 5))
plt.ylim(0, 2 * np.pi)
plt.xlim(0, 2 * np.pi)
plt.imshow(
np.asmatrix(adhoc_total).T,
interpolation="nearest",
origin="lower",
cmap="RdBu",
extent=[0, 2 * np.pi, 0, 2 * np.pi],
)
plt.scatter(
X_train[np.where(y_train[:] == 0), 0],
X_train[np.where(y_train[:] == 0), 1],
marker="s",
facecolors="w",
edgecolors="b",
label="A train",
)
plt.scatter(
X_train[np.where(y_train[:] == 1), 0],
X_train[np.where(y_train[:] == 1), 1],
marker="o",
facecolors="w",
edgecolors="r",
label="B train",
)
plt.scatter(
X_test[np.where(y_test[:] == 0), 0],
X_test[np.where(y_test[:] == 0), 1],
marker="s",
facecolors="b",
edgecolors="w",
label="A test",
)
plt.scatter(
X_test[np.where(y_test[:] == 1), 0],
X_test[np.where(y_test[:] == 1), 1],
marker="o",
facecolors="r",
edgecolors="w",
label="B test",
)
plt.legend(bbox_to_anchor=(1.05, 1), loc="upper left", borderaxespad=0.0)
plt.title("Ad hoc dataset for classification")
plt.show()
Definir el Mapa Cuántico de Características#
A continuación, configuramos el mapa cuántico de características, que codifica datos clásicos en el espacio de estados cuánticos. Aquí, usamos un QuantumCircuit para configurar una capa de rotación entrenable y un ZZFeatureMap de Qiskit para representar los datos de entrada.
[3]:
# Create a rotational layer to train. We will rotate each qubit the same amount.
training_params = ParameterVector("θ", 1)
fm0 = QuantumCircuit(2)
fm0.ry(training_params[0], 0)
fm0.ry(training_params[0], 1)
# Use ZZFeatureMap to represent input data
fm1 = ZZFeatureMap(2)
# Create the feature map, composed of our two circuits
fm = fm0.compose(fm1)
print(circuit_drawer(fm))
print(f"Trainable parameters: {training_params}")
┌──────────┐┌──────────────────────────┐
q_0: ┤ Ry(θ[0]) ├┤0 ├
├──────────┤│ ZZFeatureMap(x[0],x[1]) │
q_1: ┤ Ry(θ[0]) ├┤1 ├
└──────────┘└──────────────────────────┘
Trainable parameters: θ, ['θ[0]']
Configurar el Kernel Cuántico y el Entrenador de Kernel Cuántico#
Para entrenar el kernel cuántico, usaremos una instancia de TrainableFidelityQuantumKernel (que contiene el mapa de características y sus parámetros) y de QuantumKernelTrainer (que administra el proceso de entrenamiento).
Entrenaremos usando la técnica Quantum Kernel Alignment seleccionando la función de pérdida de kernel, SVCLoss, como entrada al QuantumKernelTrainer. Dado que esta es una pérdida compatible con Qiskit, podemos utilizar la cadena, "svc_loss"; sin embargo, ten en cuenta que la configuración predeterminada se utiliza cuando se pasa la pérdida como una cadena. Para configuraciones personalizadas, crea una instancia explícitamente con las opciones deseadas y pasa el objeto KernelLoss al QuantumKernelTrainer.
Seleccionaremos SPSA como optimizador e inicializaremos el parámetro entrenable con el argumento initial_point. Nota: La longitud de la lista pasada como el argumento initial_point debe ser igual al número de parámetros entrenables en el mapa de características.
[4]:
# Instantiate quantum kernel
quant_kernel = TrainableFidelityQuantumKernel(feature_map=fm, training_parameters=training_params)
# Set up the optimizer
cb_qkt = QKTCallback()
spsa_opt = SPSA(maxiter=10, callback=cb_qkt.callback, learning_rate=0.05, perturbation=0.05)
# Instantiate a quantum kernel trainer.
qkt = QuantumKernelTrainer(
quantum_kernel=quant_kernel, loss="svc_loss", optimizer=spsa_opt, initial_point=[np.pi / 2]
)
Entrenar el Kernel Cuántico#
Para entrenar el kernel cuántico en el conjunto de datos (muestras y etiquetas), llamamos al método fit de QuantumKernelTrainer.
La salida de QuantumKernelTrainer.fit es un objeto QuantumKernelTrainerResult. El objeto de resultados contiene los siguientes campos de clase:
optimal_parameters: Un diccionario que contiene pares {parameter: optimal value}optimal_point: El valor óptimo del parámetro encontrado en el entrenamientooptimal_value: El valor de la función de pérdida en el punto óptimooptimizer_evals: El número de evaluaciones realizadas por el optimizadoroptimizer_time: La cantidad de tiempo necesario para realizar la optimizaciónquantum_kernel: Un objetoTrainableKernelcon valores opcionales vinculados al mapa de características
[5]:
# Train the kernel using QKT directly
qka_results = qkt.fit(X_train, y_train)
optimized_kernel = qka_results.quantum_kernel
print(qka_results)
{ 'optimal_circuit': None,
'optimal_parameters': {ParameterVectorElement(θ[0]): 2.4745458584261386},
'optimal_point': array([2.47454586]),
'optimal_value': 7.399057680986741,
'optimizer_evals': 30,
'optimizer_result': None,
'optimizer_time': None,
'quantum_kernel': <qiskit_machine_learning.kernels.trainable_fidelity_quantum_kernel.TrainableFidelityQuantumKernel object at 0x7f84c120feb0>}
Ajustar y Probar el Modelo#
Podemos pasar el kernel cuántico entrenado a un modelo de machine learning, luego ajustar el modelo y probar con nuevos datos. Aquí, usaremos el QSVC de Qiskit Machine Learning para la clasificación.
[6]:
# Use QSVC for classification
qsvc = QSVC(quantum_kernel=optimized_kernel)
# Fit the QSVC
qsvc.fit(X_train, y_train)
# Predict the labels
labels_test = qsvc.predict(X_test)
# Evalaute the test accuracy
accuracy_test = metrics.balanced_accuracy_score(y_true=y_test, y_pred=labels_test)
print(f"accuracy test: {accuracy_test}")
accuracy test: 0.9
Visualizar el Proceso de Entrenamiento del Kernel#
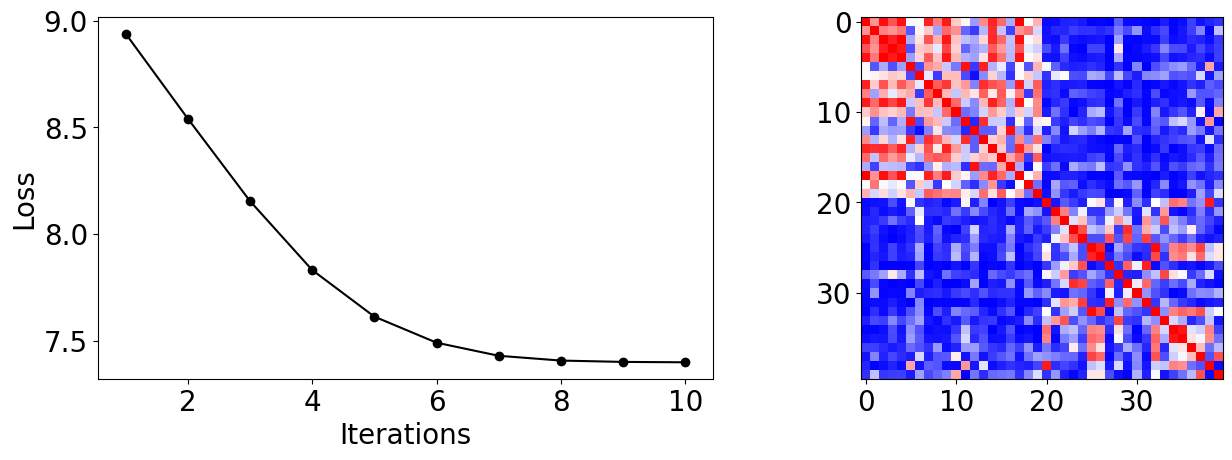
A partir de los datos de la devolución de llamada (callback), podemos graficar cómo evoluciona la pérdida durante el proceso de entrenamiento. Vemos que converge rápidamente y alcanza una alta precisión de prueba en este conjunto de datos con nuestra elección de entradas.
También podemos mostrar la matriz del kernel final, que es una medida de similitud entre las muestras de entrenamiento.
[7]:
plot_data = cb_qkt.get_callback_data() # callback data
K = optimized_kernel.evaluate(X_train) # kernel matrix evaluated on the training samples
plt.rcParams["font.size"] = 20
fig, ax = plt.subplots(1, 2, figsize=(14, 5))
ax[0].plot([i + 1 for i in range(len(plot_data[0]))], np.array(plot_data[2]), c="k", marker="o")
ax[0].set_xlabel("Iterations")
ax[0].set_ylabel("Loss")
ax[1].imshow(K, cmap=matplotlib.colormaps["bwr"])
fig.tight_layout()
plt.show()
[8]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.25.0 |
qiskit-aer | 0.13.0 |
qiskit-machine-learning | 0.7.0 |
| System information | |
| Python version | 3.8.13 |
| Python compiler | Clang 12.0.0 |
| Python build | default, Oct 19 2022 17:54:22 |
| OS | Darwin |
| CPUs | 10 |
| Memory (Gb) | 64.0 |
| Mon May 29 12:50:08 2023 IST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.