Nota
Esta página fue generada a partir de docs/tutorials/02_neural_network_classifier_and_regressor.ipynb.
Redes Neuronales de Clasificación y Regresión#
En este tutorial mostramos cómo se utiliza la NeuralNetworkClassifier y la NeuralNetworkRegressor. Ambas toman como entrada una NeuralNetwork (Cuántica) y la aprovechan en un contexto específico. En ambos casos, también ofrecemos una variante preconfigurada para mayor comodidad, el Clasificador Cuántico Variacional (Variational Quantum Classifier, VQC) y el Regresor Cuántico Variacional (Variational Quantum Regressor, VQR). El tutorial está estructurado de la siguiente manera:
Clasificación
Clasificación con una
EstimatorQNNClasificación con una
SamplerQNNClasificador Cuántico Variacional (Variational Quantum Classifier,
VQC)
Regresión
Regresión con una
EstimatorQNNRegresor Cuántico Variacional (Variational Quantum Regressor,
VQR)
[1]:
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
from qiskit import QuantumCircuit
from qiskit.circuit import Parameter
from qiskit.circuit.library import RealAmplitudes, ZZFeatureMap
from qiskit_algorithms.optimizers import COBYLA, L_BFGS_B
from qiskit_algorithms.utils import algorithm_globals
from qiskit_machine_learning.algorithms.classifiers import NeuralNetworkClassifier, VQC
from qiskit_machine_learning.algorithms.regressors import NeuralNetworkRegressor, VQR
from qiskit_machine_learning.neural_networks import SamplerQNN, EstimatorQNN
from qiskit_machine_learning.circuit.library import QNNCircuit
algorithm_globals.random_seed = 42
Clasificación#
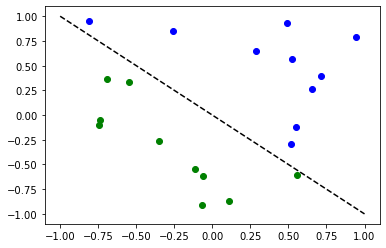
Preparamos un conjunto de datos de clasificación simple para ilustrar los siguientes algoritmos.
[2]:
num_inputs = 2
num_samples = 20
X = 2 * algorithm_globals.random.random([num_samples, num_inputs]) - 1
y01 = 1 * (np.sum(X, axis=1) >= 0) # in { 0, 1}
y = 2 * y01 - 1 # in {-1, +1}
y_one_hot = np.zeros((num_samples, 2))
for i in range(num_samples):
y_one_hot[i, y01[i]] = 1
for x, y_target in zip(X, y):
if y_target == 1:
plt.plot(x[0], x[1], "bo")
else:
plt.plot(x[0], x[1], "go")
plt.plot([-1, 1], [1, -1], "--", color="black")
plt.show()
Clasificación con una EstimatorQNN#
Primero mostramos cómo se puede usar un EstimatorQNN para la clasificación dentro de una NeuralNetworkClassifier. En este contexto, se espera que el EstimatorQNN devuelva una salida unidimensional en \([-1, +1]\). Esto solo funciona para la clasificación binaria y asignamos las dos clases a \(\{-1, +1\}\). Para simplificar la composición de un circuito cuántico parametrizado a partir de un mapa de características y un ansatz, podemos utilizar la clase QNNCircuit.
[3]:
# construct QNN with the QNNCircuit's default ZZFeatureMap feature map and RealAmplitudes ansatz.
qc = QNNCircuit(num_qubits=2)
qc.draw(output="mpl")
[3]:
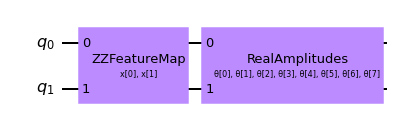
Crear una red neuronal cuántica
[4]:
estimator_qnn = EstimatorQNN(circuit=qc)
[5]:
# QNN maps inputs to [-1, +1]
estimator_qnn.forward(X[0, :], algorithm_globals.random.random(estimator_qnn.num_weights))
[5]:
array([[0.23521988]])
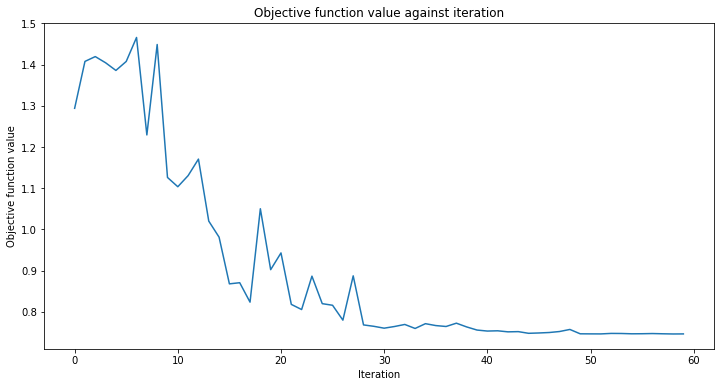
Agregaremos una función de devolución de llamada nombrada callback_graph. Esto se llamará para cada iteración del optimizador y se le pasarán dos parámetros: los pesos actuales y el valor de la función objetivo en esos pesos. Para nuestra función, agregamos el valor de la función objetivo a un arreglo para que podamos graficar la iteración frente al valor de la función objetivo y actualizar la gráfica con cada iteración. Sin embargo, puedes hacer lo que desees con una función de devolución de llamada siempre y cuando se pasen los dos parámetros mencionados.
[6]:
# callback function that draws a live plot when the .fit() method is called
def callback_graph(weights, obj_func_eval):
clear_output(wait=True)
objective_func_vals.append(obj_func_eval)
plt.title("Objective function value against iteration")
plt.xlabel("Iteration")
plt.ylabel("Objective function value")
plt.plot(range(len(objective_func_vals)), objective_func_vals)
plt.show()
[7]:
# construct neural network classifier
estimator_classifier = NeuralNetworkClassifier(
estimator_qnn, optimizer=COBYLA(maxiter=60), callback=callback_graph
)
[8]:
# create empty array for callback to store evaluations of the objective function
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit classifier to data
estimator_classifier.fit(X, y)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
# score classifier
estimator_classifier.score(X, y)
[8]:
0.8
[9]:
# evaluate data points
y_predict = estimator_classifier.predict(X)
# plot results
# red == wrongly classified
for x, y_target, y_p in zip(X, y, y_predict):
if y_target == 1:
plt.plot(x[0], x[1], "bo")
else:
plt.plot(x[0], x[1], "go")
if y_target != y_p:
plt.scatter(x[0], x[1], s=200, facecolors="none", edgecolors="r", linewidths=2)
plt.plot([-1, 1], [1, -1], "--", color="black")
plt.show()
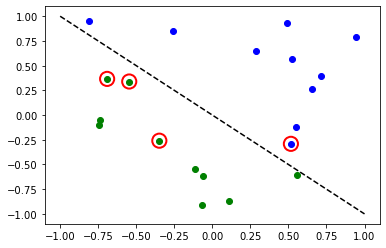
Ahora, cuando el modelo está entrenado, podemos explorar los pesos de la red neuronal. Ten en cuenta que el número de pesos está definido por el ansatz.
[10]:
estimator_classifier.weights
[10]:
array([ 7.99142399e-01, -1.02869770e+00, -1.32131512e-04, -3.47046684e-01,
1.13636802e+00, 6.56831727e-01, 2.17902158e+00, -1.08678332e+00])
Clasificación con una SamplerQNN#
A continuación mostramos cómo se puede usar una SamplerQNN para la clasificación dentro de un NeuralNetworkClassifier. En este contexto, se espera que SamplerQNN devuelva un vector de probabilidad de dimensión \(d\) como salida, donde \(d\) denota el número de clases. La primitiva Sampler subyacente devuelve cuasi-distribuciones de cadenas de bits y solo necesitamos definir un mapeo de las cadenas de bits medidas a las diferentes clases. Para la clasificación binaria usamos el mapeo de paridad. Nuevamente podemos usar la clase QNNCircuit para configurar un circuito cuántico parametrizado a partir de un mapa de características y un ansatz de nuestra elección.
[11]:
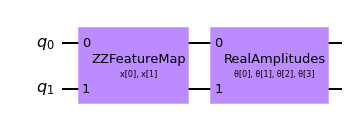
# construct a quantum circuit from the default ZZFeatureMap feature map and a customized RealAmplitudes ansatz
qc = QNNCircuit(ansatz=RealAmplitudes(num_inputs, reps=1))
qc.draw(output="mpl")
[11]:
[12]:
# parity maps bitstrings to 0 or 1
def parity(x):
return "{:b}".format(x).count("1") % 2
output_shape = 2 # corresponds to the number of classes, possible outcomes of the (parity) mapping.
[13]:
# construct QNN
sampler_qnn = SamplerQNN(
circuit=qc,
interpret=parity,
output_shape=output_shape,
)
[14]:
# construct classifier
sampler_classifier = NeuralNetworkClassifier(
neural_network=sampler_qnn, optimizer=COBYLA(maxiter=30), callback=callback_graph
)
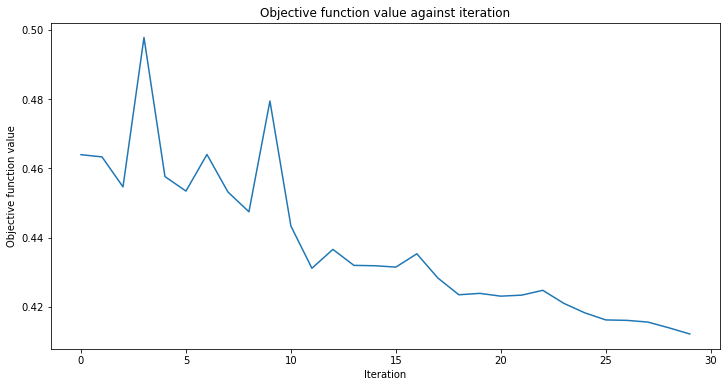
[15]:
# create empty array for callback to store evaluations of the objective function
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit classifier to data
sampler_classifier.fit(X, y01)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
# score classifier
sampler_classifier.score(X, y01)
[15]:
0.7
[16]:
# evaluate data points
y_predict = sampler_classifier.predict(X)
# plot results
# red == wrongly classified
for x, y_target, y_p in zip(X, y01, y_predict):
if y_target == 1:
plt.plot(x[0], x[1], "bo")
else:
plt.plot(x[0], x[1], "go")
if y_target != y_p:
plt.scatter(x[0], x[1], s=200, facecolors="none", edgecolors="r", linewidths=2)
plt.plot([-1, 1], [1, -1], "--", color="black")
plt.show()
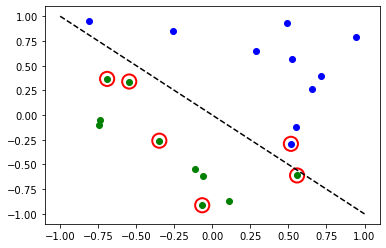
Nuevamente, una vez que el modelo está entrenado, podemos echar un vistazo a los pesos. Como configuramos explícitamente reps=1 en nuestro ansatz, podemos ver menos parámetros que en el modelo anterior.
[17]:
sampler_classifier.weights
[17]:
array([ 1.67198565, 0.46045402, -0.93462862, -0.95266092])
Clasificador Cuántico Variacional (Variational Quantum Classifier, VQC)#
El VQC es una variante especial del NeuralNetworkClassifier con una SamplerQNN. Aplica un mapeo de paridad (o extensiones a varias clases) para mapear desde la cadena de bits hasta la clasificación, lo que da como resultado un vector de probabilidad, que se interpreta como un resultado codificado con one-hot. Por defecto, aplica esta función CrossEntropyLoss que espera etiquetas dadas en el formato codificado con one-hot y devolverá predicciones en ese formato también.
[18]:
# construct feature map, ansatz, and optimizer
feature_map = ZZFeatureMap(num_inputs)
ansatz = RealAmplitudes(num_inputs, reps=1)
# construct variational quantum classifier
vqc = VQC(
feature_map=feature_map,
ansatz=ansatz,
loss="cross_entropy",
optimizer=COBYLA(maxiter=30),
callback=callback_graph,
)
[19]:
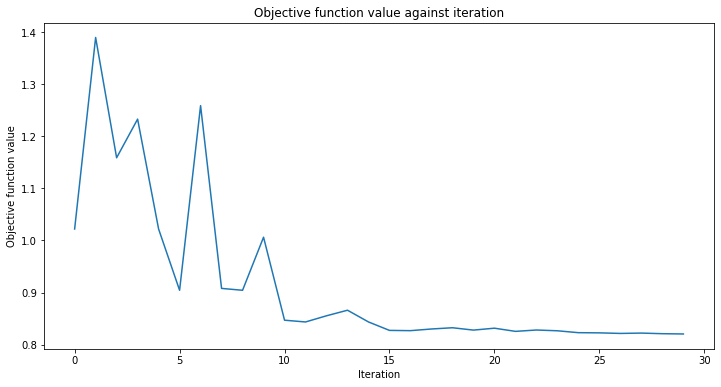
# create empty array for callback to store evaluations of the objective function
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit classifier to data
vqc.fit(X, y_one_hot)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
# score classifier
vqc.score(X, y_one_hot)
[19]:
0.8
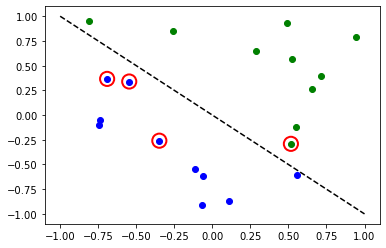
[20]:
# evaluate data points
y_predict = vqc.predict(X)
# plot results
# red == wrongly classified
for x, y_target, y_p in zip(X, y_one_hot, y_predict):
if y_target[0] == 1:
plt.plot(x[0], x[1], "bo")
else:
plt.plot(x[0], x[1], "go")
if not np.all(y_target == y_p):
plt.scatter(x[0], x[1], s=200, facecolors="none", edgecolors="r", linewidths=2)
plt.plot([-1, 1], [1, -1], "--", color="black")
plt.show()
Clases múltiples con VQC#
En esta sección generamos un conjunto de datos artificial que contiene muestras de tres clases y mostramos cómo entrenar un modelo para clasificar este conjunto de datos. Este ejemplo muestra cómo abordar problemas más interesantes en el machine learning. Por supuesto, en aras del corto tiempo de entrenamiento, preparamos un pequeño conjunto de datos. Empleamos make_classification de SciKit-Learn para generar un conjunto de datos. Hay 10 muestras en el conjunto de datos, con 2 características, lo que significa que todavía podemos tener una buena gráfica del conjunto de datos, así como características redundantes, estas características se generan como una combinación de las otras. Además, tenemos 3 clases diferentes en el conjunto de datos, cada clase tiene un tipo de centroide y establecemos la separación de clases en 2.0, un ligero aumento del valor predeterminado de 1.0 para facilitar el problema de clasificación.
Una vez que el conjunto de datos es generado, escalamos las características en el rango [0, 1].
[21]:
from sklearn.datasets import make_classification
from sklearn.preprocessing import MinMaxScaler
X, y = make_classification(
n_samples=10,
n_features=2,
n_classes=3,
n_redundant=0,
n_clusters_per_class=1,
class_sep=2.0,
random_state=algorithm_globals.random_seed,
)
X = MinMaxScaler().fit_transform(X)
Veamos cómo se ve nuestro conjunto de datos.
[22]:
plt.scatter(X[:, 0], X[:, 1], c=y)
[22]:
<matplotlib.collections.PathCollection at 0x7fd5e072c250>

También transformamos las etiquetas y las convertimos en categóricas.
[23]:
y_cat = np.empty(y.shape, dtype=str)
y_cat[y == 0] = "A"
y_cat[y == 1] = "B"
y_cat[y == 2] = "C"
print(y_cat)
['A' 'A' 'B' 'C' 'C' 'A' 'B' 'B' 'A' 'C']
Creamos una instancia de VQC similar al ejemplo anterior, pero en este caso pasamos un conjunto mínimo de parámetros. En lugar de un mapa de características y un ansatz, pasamos solo la cantidad de qubits que es igual a la cantidad de características en el conjunto de datos, un optimizador con un bajo número de iteraciones para reducir el tiempo de entrenamiento, una instancia cuántica (quantum instance) y una devolución de llamada (callback) para observar el progreso.
[24]:
vqc = VQC(
num_qubits=2,
optimizer=COBYLA(maxiter=30),
callback=callback_graph,
)
Inicia el proceso de entrenamiento de la misma forma que en los ejemplos anteriores.
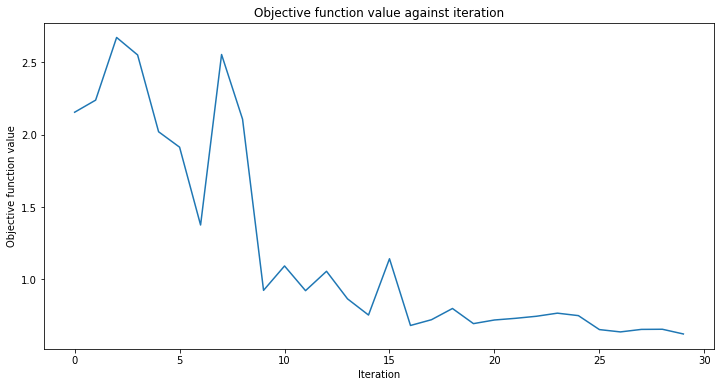
[25]:
# create empty array for callback to store evaluations of the objective function
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit classifier to data
vqc.fit(X, y_cat)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
# score classifier
vqc.score(X, y_cat)
[25]:
0.9
A pesar de que tuvimos el bajo número de iteraciones, logramos una puntuación bastante buena. Veamos el resultado del método predict y comparemos el resultado con la verdad fundamental.
[26]:
predict = vqc.predict(X)
print(f"Predicted labels: {predict}")
print(f"Ground truth: {y_cat}")
Predicted labels: ['A' 'A' 'B' 'C' 'C' 'A' 'B' 'B' 'A' 'B']
Ground truth: ['A' 'A' 'B' 'C' 'C' 'A' 'B' 'B' 'A' 'C']
Regresión#
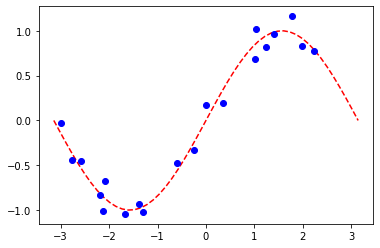
Preparamos un conjunto de datos de regresión simple para ilustrar los siguientes algoritmos.
[27]:
num_samples = 20
eps = 0.2
lb, ub = -np.pi, np.pi
X_ = np.linspace(lb, ub, num=50).reshape(50, 1)
f = lambda x: np.sin(x)
X = (ub - lb) * algorithm_globals.random.random([num_samples, 1]) + lb
y = f(X[:, 0]) + eps * (2 * algorithm_globals.random.random(num_samples) - 1)
plt.plot(X_, f(X_), "r--")
plt.plot(X, y, "bo")
plt.show()
Regresión con una EstimatorQNN#
Aquí restringimos la regresión con una EstimatorQNN que devuelve valores entre \([-1, +1]\). Se podrían construir modelos más complejos y también multidimensionales, así como basados en SamplerQNN, pero eso excede el alcance de este tutorial.
[28]:
# construct simple feature map
param_x = Parameter("x")
feature_map = QuantumCircuit(1, name="fm")
feature_map.ry(param_x, 0)
# construct simple ansatz
param_y = Parameter("y")
ansatz = QuantumCircuit(1, name="vf")
ansatz.ry(param_y, 0)
# construct a circuit
qc = QNNCircuit(feature_map=feature_map, ansatz=ansatz)
# construct QNN
regression_estimator_qnn = EstimatorQNN(circuit=qc)
[29]:
# construct the regressor from the neural network
regressor = NeuralNetworkRegressor(
neural_network=regression_estimator_qnn,
loss="squared_error",
optimizer=L_BFGS_B(maxiter=5),
callback=callback_graph,
)
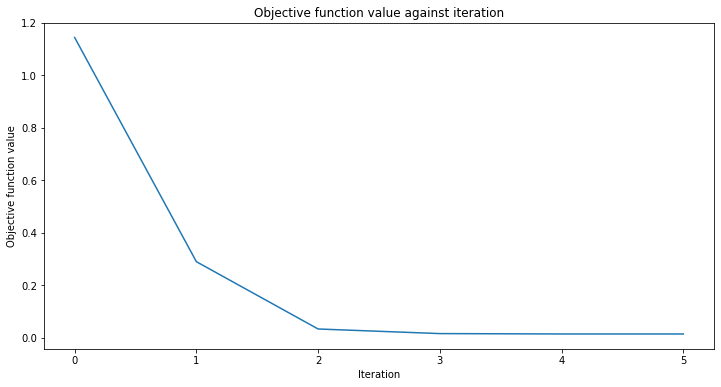
[30]:
# create empty array for callback to store evaluations of the objective function
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit to data
regressor.fit(X, y)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
# score the result
regressor.score(X, y)
[30]:
0.9769994291935522
[31]:
# plot target function
plt.plot(X_, f(X_), "r--")
# plot data
plt.plot(X, y, "bo")
# plot fitted line
y_ = regressor.predict(X_)
plt.plot(X_, y_, "g-")
plt.show()
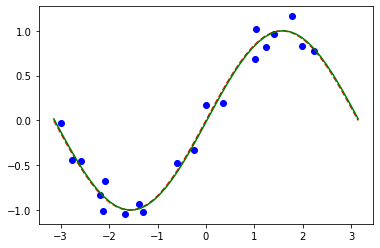
De manera similar a los modelos de clasificación, podemos obtener una matriz de pesos entrenados consultando una propiedad correspondiente del modelo. En este modelo solo tenemos un parámetro arriba definido como param_y.
[32]:
regressor.weights
[32]:
array([-1.58870599])
Regresión con el Regresor Cuántico Variacional (Variational Quantum Regressor, VQR)#
Similar al VQC para la clasificación, el VQR es una variante especial del NeuralNetworkRegressor con una EstimatorQNN. De forma predeterminada, considera la función L2Loss para minimizar el error cuadrático medio entre las predicciones y los objetivos.
[33]:
vqr = VQR(
feature_map=feature_map,
ansatz=ansatz,
optimizer=L_BFGS_B(maxiter=5),
callback=callback_graph,
)
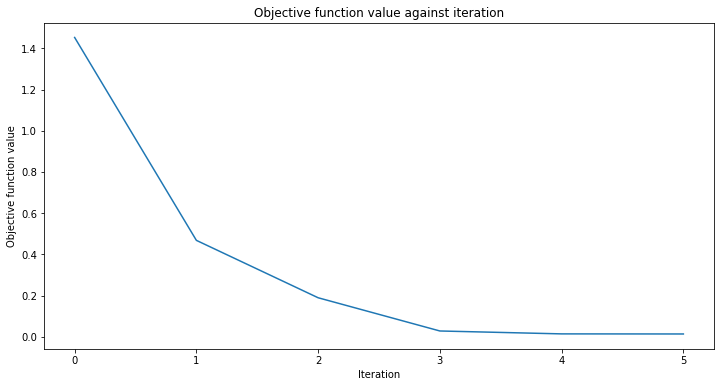
[34]:
# create empty array for callback to store evaluations of the objective function
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit regressor
vqr.fit(X, y)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
# score result
vqr.score(X, y)
[34]:
0.9769955693935385
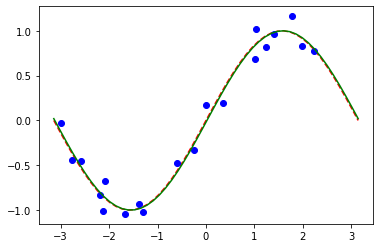
[35]:
# plot target function
plt.plot(X_, f(X_), "r--")
# plot data
plt.plot(X, y, "bo")
# plot fitted line
y_ = vqr.predict(X_)
plt.plot(X_, y_, "g-")
plt.show()
[36]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.24.0 |
qiskit-aer | 0.12.0 |
qiskit-ignis | 0.6.0 |
qiskit-ibmq-provider | 0.20.2 |
qiskit | 0.43.0 |
qiskit-machine-learning | 0.7.0 |
| System information | |
| Python version | 3.8.8 |
| Python compiler | Clang 10.0.0 |
| Python build | default, Apr 13 2021 12:59:45 |
| OS | Darwin |
| CPUs | 8 |
| Memory (Gb) | 32.0 |
| Tue Jun 13 16:39:30 2023 CEST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.