Nota

Esta página fue generada a partir de docs/tutorials/04_torch_qgan.ipynb.

Implementación de PyTorch qGAN#

Descripción General#

Este tutorial presenta paso a paso cómo construir un algoritmo de Red de Adversarios Generativos Cuántica basado en PyTorch.

El tutorial está estructurado de la siguiente manera:

Introducción
Datos y Representación
Definiciones de las Redes Neuronales
Configuración del Ciclo de Entrenamiento
Entrenamiento del Modelo
Resultados: Funciones de Densidad Acumulativa
Conclusión

1. Introducción#

El qGAN [1] es un algoritmo híbrido cuántico-clásico utilizado para tareas de modelado generativo. El algoritmo utiliza la interacción de un generador cuántico \(G_{\theta}\), es decir, un ansatz (circuito cuántico parametrizado), y un discriminador clásico \(D_{\phi}\), una red neuronal, para aprender la distribución de probabilidad subyacente dados los datos de entrenamiento.

El generador y el discriminador se entrenan en pasos de optimización alternantes, donde el generador apunta a generar probabilidades que serán clasificadas por el discriminador como valores de datos de entrenamiento (es decir, probabilidades de la distribución de entrenamiento real), y el discriminador trata de diferenciar entre distribución original y probabilidades del generador (en otras palabras, distinguir las distribuciones real y generada). El objetivo final es que el generador cuántico aprenda una representación para la distribución de probabilidad objetivo. El generador cuántico entrenado puede, por lo tanto, usarse para cargar un estado cuántico que es un modelo aproximado de la distribución objetivo.

Referencias:

[1] Zoufal et al., Quantum Generative Adversarial Networks for learning and loading random distributions

1.1. qGANs para Cargar Distribuciones Aleatorias#

Dadas las muestras de datos \(k\)-dimensionales, empleamos una Red de Adversarios Generativos cuántica (quantum Generative Adversarial Network, qGAN) para conocer una distribución aleatoria y cargarla directamente en un estado cuántico:

\[\big| g_{\theta}\rangle = \sum_{j=0}^{2^n-1} \sqrt{p_{\theta}^{j}}\big| j \rangle\]

donde \(p_{\theta}^{j}\) describen las probabilidades de ocurrencia de los estados base \(\big| j\rangle\).

El objetivo del entrenamiento qGAN es generar un estado \(\big| g_{\theta}\rangle\) donde \(p_{\theta}^{j}\), para \(j\in \left\{0, \ldots, {2^n-1} \right\}\), describe una distribución de probabilidad cercana a la distribución subyacente a los datos de entrenamiento \(X=\left\{x^0, \ldots, x^{k-1} \right\}\).

Para obtener más detalles, consulta Quantum Generative Adversarial Networks for Learning and Loading Random Distributions Zoufal, Lucchi, Woerner [2019].

Para un ejemplo de cómo utilizar una qGAN entrenada en una aplicación, la fijación de precios de derivados financieros, consulta el tutorial Fijación de Precios de Opciones con qGANs.

2. Datos y Representación#

Primero, necesitamos cargar nuestros datos de entrenamiento \(X\).

En este tutorial, los datos de entrenamiento están dados por una distribución normal multivariante 2D.

El objetivo del generador es aprender a representar dicha distribución, y el generador entrenado debe corresponder a un estado cuántico de \(n\) qubits \begin{equation} |g_{\text{trained}}\rangle=\sum\limits_{j=0}^{k-1}\sqrt{p_{j}}|x_{j}\rangle, \end{equation} donde el estado base \(|x_{j}\rangle\) representa los elementos de datos en el conjunto de datos de entrenamiento \(X={x_0, \ldots, x_{k-1}}\) con \(k\leq 2^n\) y \(p_j\) se refiere a la probabilidad de muestreo de \(|x_{j}\rangle\).

Para facilitar esta representación, necesitamos mapear las muestras de la distribución normal multivariante a valores discretos. La cantidad de valores que se pueden representar depende de la cantidad de qubits utilizados para el mapeo. Por lo tanto, la resolución de datos se define por el número de qubits. Si usamos \(3\) qubits para representar una característica, tenemos \(2^3 = 8\) valores discretos.

Primero comenzamos fijando semillas en los generadores de números aleatorios para la reproducibilidad del resultado en este tutorial.

[1]:

import torch
from qiskit_algorithms.utils import algorithm_globals

algorithm_globals.random_seed = 123456
_ = torch.manual_seed(123456)  # suppress output

Fijamos el número de dimensiones, el número de discretización y calculamos el número de qubits requeridos como \(2^3 = 8\).

[2]:

import numpy as np

num_dim = 2
num_discrete_values = 8
num_qubits = num_dim * int(np.log2(num_discrete_values))

Luego, preparamos una distribución discreta a partir de la distribución normal 2D continua. Evaluamos la función de densidad de probabilidad continua (probability density function, PDF) en la cuadrícula \((-2, 2)^2\) con una discretización de \(8\) valores por función. Por lo tanto, tenemos \(64\) valores de la PDF. Como esta será una distribución discreta, normalizamos las probabilidades obtenidas.

[3]:

from scipy.stats import multivariate_normal

coords = np.linspace(-2, 2, num_discrete_values)
rv = multivariate_normal(mean=[0.0, 0.0], cov=[[1, 0], [0, 1]], seed=algorithm_globals.random_seed)
grid_elements = np.transpose([np.tile(coords, len(coords)), np.repeat(coords, len(coords))])
prob_data = rv.pdf(grid_elements)
prob_data = prob_data / np.sum(prob_data)

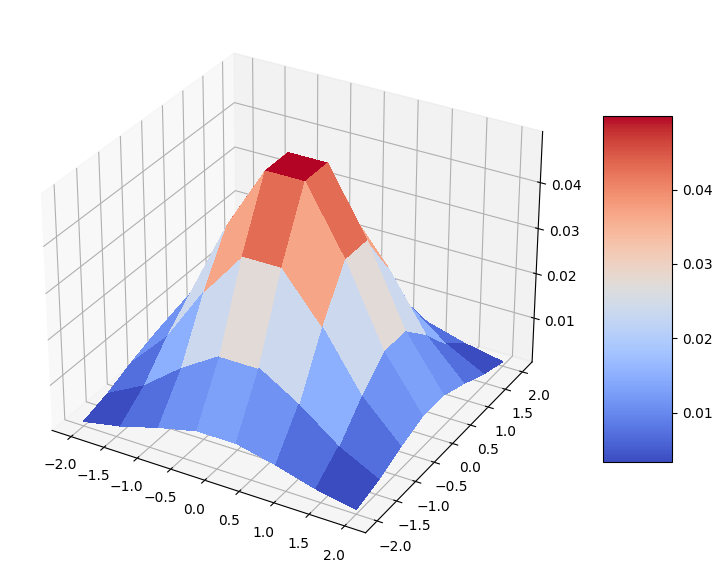
Visualicemos nuestra distribución. Es una buena distribución normal bivariada en forma de campana en una cuadrícula discreta.

[4]:

import matplotlib.pyplot as plt
from matplotlib import cm

mesh_x, mesh_y = np.meshgrid(coords, coords)
grid_shape = (num_discrete_values, num_discrete_values)

fig, ax = plt.subplots(figsize=(9, 9), subplot_kw={"projection": "3d"})
prob_grid = np.reshape(prob_data, grid_shape)
surf = ax.plot_surface(mesh_x, mesh_y, prob_grid, cmap=cm.coolwarm, linewidth=0, antialiased=False)
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()

../_images/tutorials_04_torch_qgan_7_0.png

3. Definiciones de las Redes Neuronales#

En esta sección definimos dos redes neuronales como se describe anteriormente:

Un generador cuántico como una red neuronal cuántica.
Un discriminador clásico como una red neuronal basada en PyTorch.

3.1. Definición de la red neuronal cuántica ansatz#

Ahora, definimos el circuito cuántico parametrizado \(G\left(\boldsymbol{\theta}\right)\) con \(\boldsymbol{\theta} = {\theta_1, ..., \theta_k}\) que será uilizado en nuestro generador cuántico.

Para implementar el generador cuántico, elegimos un ansatz eficiente en hardware con \(6\) repeticiones. El ansatz implementa rotaciones \(R_Y\), \(R_Z\) y compuertas \(CX\) que toman una distribución uniforme como estado de entrada. En particular, para \(k>1\) los parámetros del generador deben elegirse con cuidado. Por ejemplo, la profundidad del circuito debe ser mayor que \(1\) porque las profundidades de circuito más altas permiten la representación de estructuras más complejas. Aquí, construimos un circuito bastante profundo con una gran cantidad de parámetros para poder capturar y representar adecuadamente la distribución.

[5]:

from qiskit import QuantumCircuit
from qiskit.circuit.library import EfficientSU2

qc = QuantumCircuit(num_qubits)
qc.h(qc.qubits)

ansatz = EfficientSU2(num_qubits, reps=6)
qc.compose(ansatz, inplace=True)

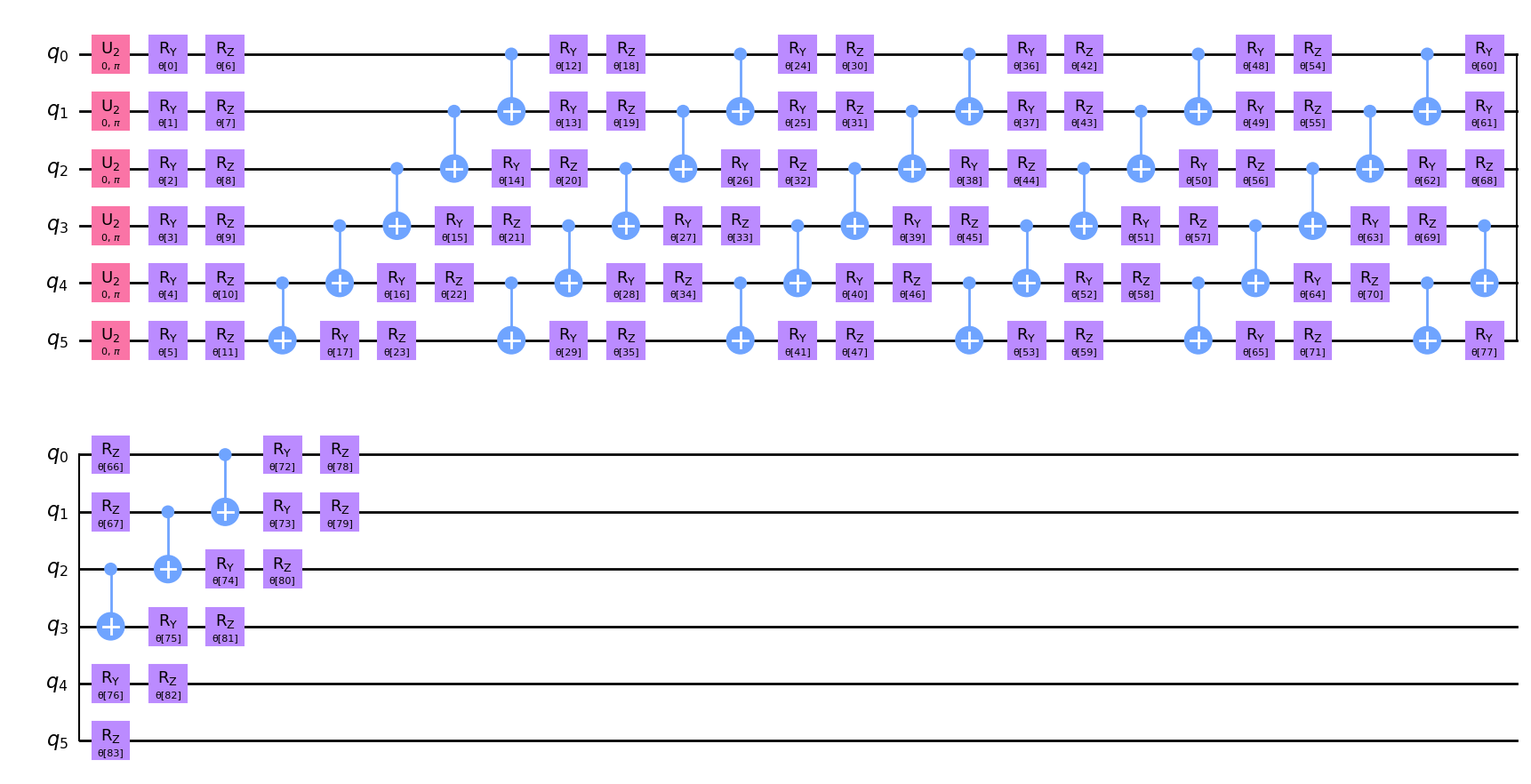
Dibujemos nuestro circuito y veamos cómo se ve. En la gráfica podemos notar un patrón que aparece \(6\) veces.

[6]:

qc.decompose().draw("mpl")

[6]:

../_images/tutorials_04_torch_qgan_11_0.png

Imprimamos el número de parámetros entrenables.

[7]:

qc.num_parameters

[7]:

3.2. Definición del generador cuántico#

Comenzamos definiendo el generador creando un muestreador para el ansatz. La implementación de referencia está basada en vector de estado, por lo que devuelve probabilidades exactas como resultado de la ejecución del circuito. Agregamos el parámetro shots para agregar algo de ruido a los resultados. En este caso, la implementación muestra probabilidades de la distribución multinomial construida a partir de las cuasi probabilidades medidas. Y, como de costumbre, fijamos la semilla con fines de reproducibilidad.

[8]:

from qiskit.primitives import Sampler

shots = 10000
sampler = Sampler(options={"shots": shots, "seed": algorithm_globals.random_seed})

A continuación, definimos una función que crea el generador cuántico a partir de un circuito cuántico parametrizado dado. Dentro de esta función, creamos una red neuronal que devuelve la distribución de cuasi probabilidad evaluada por el Sampler subyacente. Fijamos initial_weights con fines de reproducibilidad. Al final, envolvemos la red neuronal cuántica creada en TorchConnector para hacer uso del entrenamiento basado en PyTorch.

[9]:

from qiskit_machine_learning.connectors import TorchConnector
from qiskit_machine_learning.neural_networks import SamplerQNN


def create_generator() -> TorchConnector:
    qnn = SamplerQNN(
        circuit=qc,
        sampler=sampler,
        input_params=[],
        weight_params=qc.parameters,
        sparse=False,
    )

    initial_weights = algorithm_globals.random.random(qc.num_parameters)
    return TorchConnector(qnn, initial_weights)

3.3. Definición del discriminador clásico#

Después, definimos una red neuronal clásica basada en PyTorch que representa el discriminador clásico. Los gradientes subyacentes se pueden calcular automáticamente con PyTorch.

[10]:

from torch import nn


class Discriminator(nn.Module):
    def __init__(self, input_size):
        super(Discriminator, self).__init__()

        self.linear_input = nn.Linear(input_size, 20)
        self.leaky_relu = nn.LeakyReLU(0.2)
        self.linear20 = nn.Linear(20, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, input: torch.Tensor) -> torch.Tensor:
        x = self.linear_input(input)
        x = self.leaky_relu(x)
        x = self.linear20(x)
        x = self.sigmoid(x)
        return x

3.4. Crear un generador y un discriminador#

Ahora creamos un generador y un discriminador.

[11]:

generator = create_generator()
discriminator = Discriminator(num_dim)

4. Configuración del Ciclo de Entrenamiento#

En esta sección configuramos:

Una función de pérdida para el generador y el discriminador.
Optimizadores para ambos.
Una función de utilidad de graficado para visualizar el proceso de entrenamiento.

4.1. Definición de las funciones de pérdida#

Queremos entrenar el generador y el discriminador con entropía cruzada binaria como la función de pérdida:

\[L\left(\boldsymbol{\theta}\right)=\sum_jp_j\left(\boldsymbol{\theta}\right)\left[y_j\log(x_j) + (1-y_j)\log(1-x_j)\right],\]

donde \(x_j\) se refiere a una muestra de datos, mientras que \(y_j\) a la etiqueta correspondiente.

Dado que binary_cross_entropy de PyTorch no es diferenciable con respecto a los pesos, implementamos la función de pérdida manualmente para poder evaluar gradientes.

[12]:

def adversarial_loss(input, target, w):
    bce_loss = target * torch.log(input) + (1 - target) * torch.log(1 - input)
    weighted_loss = w * bce_loss
    total_loss = -torch.sum(weighted_loss)
    return total_loss

4.2. Definición de los optimizadores#

Para entrenar el generador y el discriminador, necesitamos definir esquemas de optimización. A continuación, empleamos un optimizador basado en el momento llamado Adam, consulta Kingma et al., Adam: A method for stochastic optimization para obtener más detalles.

[13]:

from torch.optim import Adam

lr = 0.01  # learning rate
b1 = 0.7  # first momentum parameter
b2 = 0.999  # second momentum parameter

generator_optimizer = Adam(generator.parameters(), lr=lr, betas=(b1, b2), weight_decay=0.005)
discriminator_optimizer = Adam(
    discriminator.parameters(), lr=lr, betas=(b1, b2), weight_decay=0.005
)

4.3. Visualización del proceso de entrenamiento#

Visualizaremos lo que sucede durante el entrenamiento graficando la evolución de las funciones de pérdida del generador y del discriminador durante el entrenamiento, así como el progreso en la entropía relativa entre la distribución entrenada y objetivo. Definimos una función que grafique las funciones de pérdida y la entropía relativa. Llamamos a esta función una vez que se completa una época de entrenamiento.

La visualización del proceso de entrenamiento comienza cuando los datos de entrenamiento se recopilan en dos épocas.

[14]:

from IPython.display import clear_output


def plot_training_progress():
    # we don't plot if we don't have enough data
    if len(generator_loss_values) < 2:
        return

    clear_output(wait=True)
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(18, 9))

    # Generator Loss
    ax1.set_title("Loss")
    ax1.plot(generator_loss_values, label="generator loss", color="royalblue")
    ax1.plot(discriminator_loss_values, label="discriminator loss", color="magenta")
    ax1.legend(loc="best")
    ax1.set_xlabel("Iteration")
    ax1.set_ylabel("Loss")
    ax1.grid()

    # Relative Entropy
    ax2.set_title("Relative entropy")
    ax2.plot(entropy_values)
    ax2.set_xlabel("Iteration")
    ax2.set_ylabel("Relative entropy")
    ax2.grid()

    plt.show()

5. Entrenamiento del Modelo#

En el ciclo de entrenamiento monitoreamos no solo las funciones de pérdida, sino también la entropía relativa. La entropía relativa describe una métrica de distancia para las distribuciones. Por lo tanto, podemos usarla para comparar qué tan cerca/lejos está la distribución entrenada de la distribución objetivo.

Ahora, estamos listos para entrenar nuestro modelo. Puede llevar algo de tiempo entrenar al modelo, así que ten paciencia.

[15]:

import time
from scipy.stats import multivariate_normal, entropy

n_epochs = 50

num_qnn_outputs = num_discrete_values**num_dim

generator_loss_values = []
discriminator_loss_values = []
entropy_values = []

start = time.time()
for epoch in range(n_epochs):

    valid = torch.ones(num_qnn_outputs, 1, dtype=torch.float)
    fake = torch.zeros(num_qnn_outputs, 1, dtype=torch.float)

    # Configure input
    real_dist = torch.tensor(prob_data, dtype=torch.float).reshape(-1, 1)

    # Configure samples
    samples = torch.tensor(grid_elements, dtype=torch.float)
    disc_value = discriminator(samples)

    # Generate data
    gen_dist = generator(torch.tensor([])).reshape(-1, 1)

    # Train generator
    generator_optimizer.zero_grad()
    generator_loss = adversarial_loss(disc_value, valid, gen_dist)

    # store for plotting
    generator_loss_values.append(generator_loss.detach().item())

    generator_loss.backward(retain_graph=True)
    generator_optimizer.step()

    # Train Discriminator
    discriminator_optimizer.zero_grad()

    real_loss = adversarial_loss(disc_value, valid, real_dist)
    fake_loss = adversarial_loss(disc_value, fake, gen_dist.detach())
    discriminator_loss = (real_loss + fake_loss) / 2

    # Store for plotting
    discriminator_loss_values.append(discriminator_loss.detach().item())

    discriminator_loss.backward()
    discriminator_optimizer.step()

    entropy_value = entropy(gen_dist.detach().squeeze().numpy(), prob_data)
    entropy_values.append(entropy_value)

    plot_training_progress()

elapsed = time.time() - start
print(f"Fit in {elapsed:0.2f} sec")

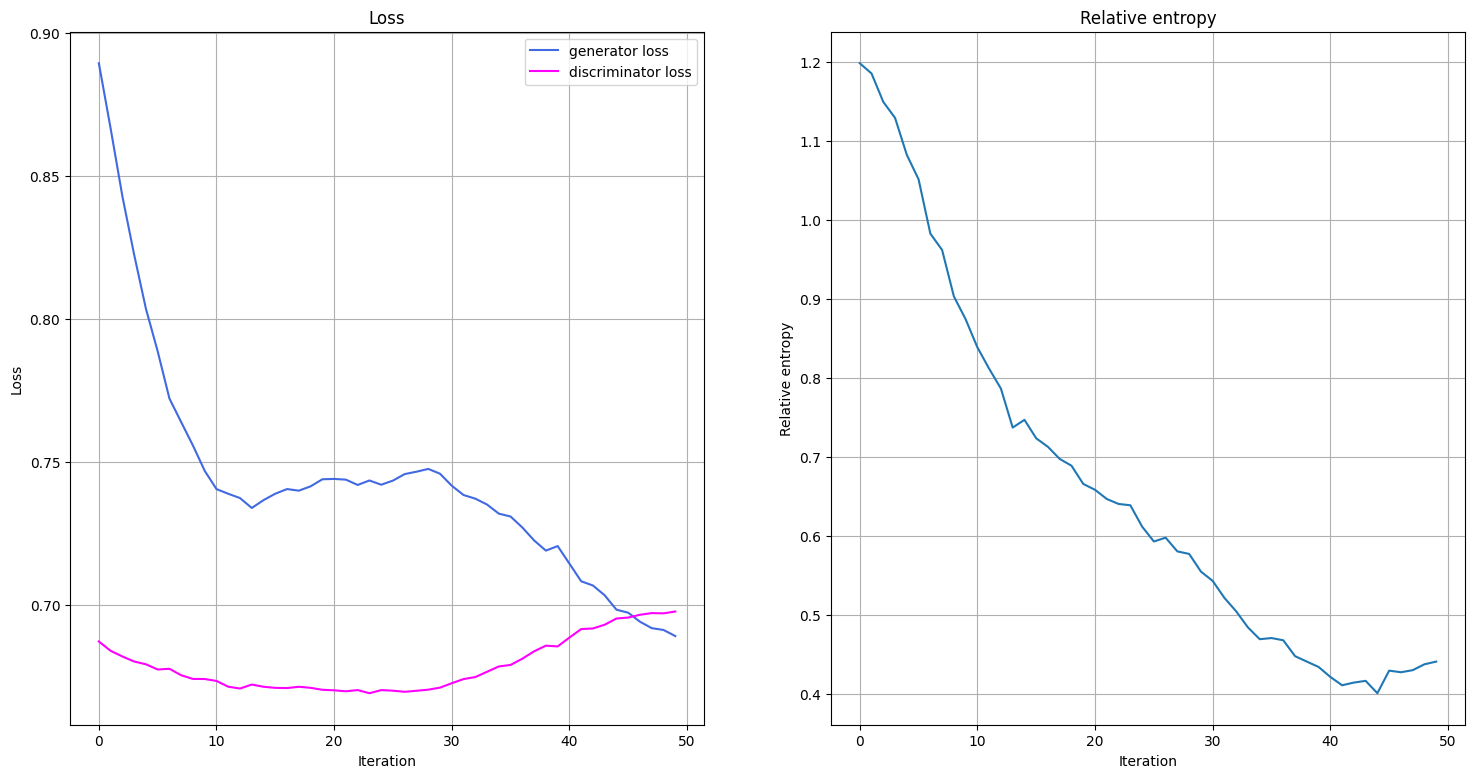
../_images/tutorials_04_torch_qgan_29_0.png

Fit in 70.86 sec

6. Resultados: Funciones de Densidad Acumulativa#

En esta sección, comparamos la función de distribución acumulativa (cumulative distribution function, CDF) de la distribución entrenada con la CDF de la distribución objetivo.

Primero, generamos una nueva distribución de probabilidad con el autograd de PyTorch desactivado, ya que no vamos a entrenar más el modelo.

[16]:

with torch.no_grad():
    generated_probabilities = generator().numpy()

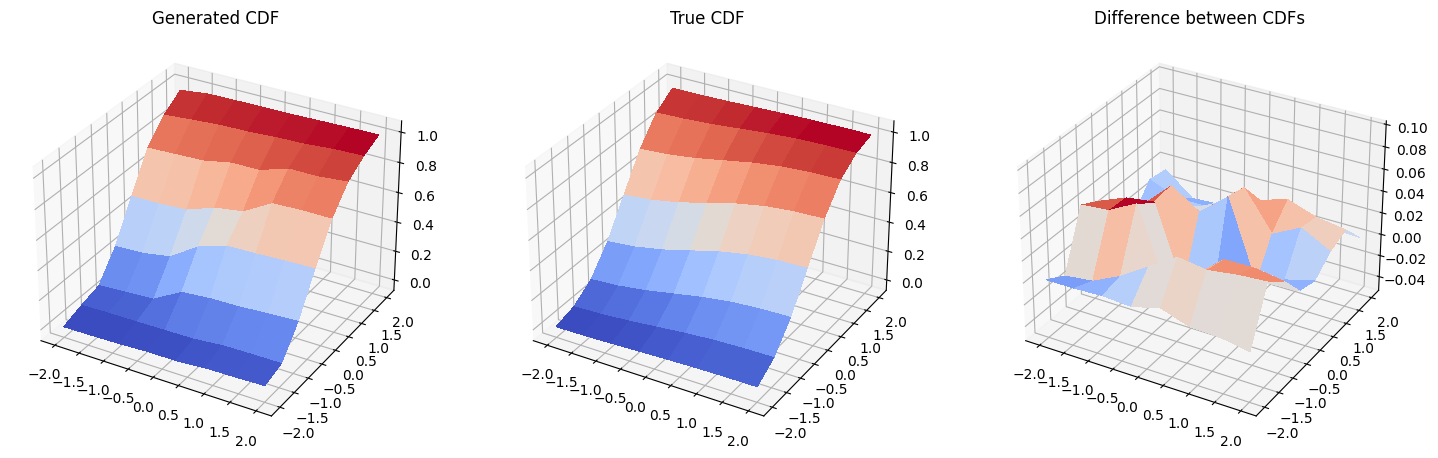
Y luego, graficamos las funciones de distribución acumulativa de la distribución generada, la distribución original y la diferencia entre ellas. Ten cuidado, la escala en la tercera gráfica no es la misma que en la primera y segunda gráfica, y la diferencia real entre las dos CDF graficadas es bastante pequeña.

[17]:

fig = plt.figure(figsize=(18, 9))

# Generated CDF
gen_prob_grid = np.reshape(np.cumsum(generated_probabilities), grid_shape)

ax1 = fig.add_subplot(1, 3, 1, projection="3d")
ax1.set_title("Generated CDF")
ax1.plot_surface(mesh_x, mesh_y, gen_prob_grid, linewidth=0, antialiased=False, cmap=cm.coolwarm)
ax1.set_zlim(-0.05, 1.05)

# Real CDF
real_prob_grid = np.reshape(np.cumsum(prob_data), grid_shape)

ax2 = fig.add_subplot(1, 3, 2, projection="3d")
ax2.set_title("True CDF")
ax2.plot_surface(mesh_x, mesh_y, real_prob_grid, linewidth=0, antialiased=False, cmap=cm.coolwarm)
ax2.set_zlim(-0.05, 1.05)

# Difference
ax3 = fig.add_subplot(1, 3, 3, projection="3d")
ax3.set_title("Difference between CDFs")
ax3.plot_surface(
    mesh_x, mesh_y, real_prob_grid - gen_prob_grid, linewidth=2, antialiased=False, cmap=cm.coolwarm
)
ax3.set_zlim(-0.05, 0.1)
plt.show()

../_images/tutorials_04_torch_qgan_33_0.png

7. Conclusión#

Las redes de adversarios generativos cuánticas emplean la interacción de un generador y un discriminador para mapear una representación aproximada de una distribución de probabilidad subyacente a muestras de datos dadas en un canal cuántico. Este tutorial presenta una implementación autónoma de qGAN basada en PyTorch, donde el generador está dado por un canal cuántico, es decir, un circuito cuántico variacional, y el discriminador por una red neuronal clásica, y analiza la aplicación de aprendizaje eficiente y carga de distribuciones de probabilidad genéricas en estados cuánticos. La carga requiere compuertas \(\mathscr{O}\left(poly\left(n\right)\right)\) y, por lo tanto, puede permitir el uso de algoritmos cuánticos potencialmente ventajosos.

[18]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
`qiskit-terra`	0.23.1
`qiskit-aer`	0.12.0
`qiskit-machine-learning`	0.6.0
System information
Python version	3.8.13
Python compiler	Clang 12.0.0
Python build	default, Oct 19 2022 17:54:22
OS	Darwin
CPUs	10
Memory (Gb)	64.0
Mon Feb 20 17:09:10 2023 GMT

This code is a part of Qiskit

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.