Nota

Esta página fue generada a partir de docs/tutorials/10_effective_dimension.ipynb.

Dimensión Efectiva de las Redes Neuronales de Qiskit

En este tutorial, aprovecharemos las clases EffectiveDimension y LocalEffectiveDimension para evaluar el poder de los modelos de redes neuronales cuánticas. Son métricas basadas en la geometría de la información que conectan con nociones como la entrenabilidad, la expresibilidad o la capacidad de generalización.

Antes de profundizar en el ejemplo de código, explicaremos brevemente cuál es la diferencia entre estas dos métricas y por qué son relevantes para el estudio de las redes neuronales cuánticas. Se puede encontrar más información sobre la dimensión efectiva global en este artículo, mientras que la dimensión efectiva local se introdujo en un trabajo posterior.

1. Dimensión Efectiva Global vs. Local

Tanto el modelo de machine learning clásico como el cuántico comparten un objetivo común: ser bueno para generalizar, es decir, aprender información de los datos y aplicarla en datos ocultos.

Encontrar una buena métrica para evaluar esta capacidad no es un asunto trivial. En The Power of Quantum Neural Networks, los autores presentan la dimensión efectiva global como un indicador útil de qué tan bien un modelo en particular podrá desempeñarse con nuevos datos. En Effective Dimension of Machine Learning Models, la dimensión efectiva local se propone como una nueva medida de capacidad que limita el error de generalización de los modelos de machine learning.

La diferencia clave entre la dimensión efectiva global (clase EffectiveDimension) y local (clase LocalEffectiveDimension) no está en la forma en que se calculan, sino en la naturaleza del espacio de parámetros que se analiza. La dimensión efectiva global incorpora el espacio de parámetros completo del modelo y se calcula a partir de una gran cantidad de conjuntos de parámetros (peso). Por otro lado, la dimensión efectiva local se enfoca en qué tan bien el modelo entrenado puede generalizar a nuevos datos y qué tan expresiva puede ser. Por lo tanto, la dimensión efectiva local se calcula a partir de un solo conjunto de muestras de peso (resultado del entrenamiento). Esta diferencia es pequeña en términos de implementación práctica, pero bastante relevante a nivel conceptual.

2. El Algoritmo de Dimensión Efectiva

Los algoritmos de dimensión efectiva global y local utilizan la matriz de Información de Fisher para proporcionar una medida de la complejidad. Los detalles sobre cómo se calcula esta matriz se proporcionan en el artículo de referencia, pero en términos generales, esta matriz captura qué tan sensible es la salida de una red neuronal a los cambios en el espacio de parámetros de la red.

En particular, este algoritmo sigue 4 pasos principales:

1. Simulación de Monte Carlo: los pasos hacia adelante y hacia atrás (gradientes) de la red neuronal se calculan para cada par de muestras de entrada y peso.

2. Cálculo de Matriz de Fisher: estos resultados y gradientes se utilizan para calcular la Matriz de Información de Fisher.

3. Normalización de la Matriz de Fisher: promediando todas las muestras de entrada y dividiendo por la traza de la matriz

4. Cálculo de la Dimensión Efectiva: según la fórmula de Abbas et al.

3. Ejemplo Básico (SamplerQNN)

Este ejemplo muestra cómo configurar un problema de modelo QNN y ejecutar el algoritmo de dimensión efectiva global. Tanto SamplerQNN de Qiskit (que se muestra en este ejemplo) como EstimatorQNN (que se muestra en un ejemplo posterior) se pueden usar con la clase EffectiveDimension.

Partimos con las importaciones requeridas y una semilla fija para el generador de números aleatorios con fines de reproducibilidad.

# Necessary imports
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
from qiskit import QuantumCircuit
from qiskit.circuit.library import ZFeatureMap, RealAmplitudes
from qiskit_algorithms.optimizers import COBYLA
from qiskit_algorithms.utils import algorithm_globals
from sklearn.datasets import make_classification
from sklearn.preprocessing import MinMaxScaler

from qiskit_machine_learning.circuit.library import QNNCircuit
from qiskit_machine_learning.algorithms.classifiers import NeuralNetworkClassifier
from qiskit_machine_learning.neural_networks import EffectiveDimension, LocalEffectiveDimension
from qiskit_machine_learning.neural_networks import SamplerQNN, EstimatorQNN

# set random seed
algorithm_globals.random_seed = 42

3.1 Definir la QNN

El primer paso para crear un SamplerQNN es definir un mapa de características parametrizado y un ansatz. En este ejemplo de juguete, usaremos 3 qubits y la clase QNNCircuit para simplificar la composición de un mapa de características y un circuito ansatz. El circuito resultante luego se utiliza en la clase SamplerQNN.

num_qubits = 3
# combine a custom feature map and ansatz into a single circuit
qc = QNNCircuit(
    feature_map=ZFeatureMap(feature_dimension=num_qubits, reps=1),
    ansatz=RealAmplitudes(num_qubits, reps=1),
)
qc.draw("mpl")

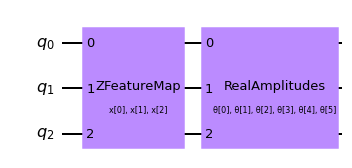
El circuito parametrizado se puede enviar junto con un mapa de interpretación opcional (paridad en este caso) al constructor de SamplerQNN.

# parity maps bitstrings to 0 or 1
def parity(x):
    return "{:b}".format(x).count("1") % 2


output_shape = 2  # corresponds to the number of classes, possible outcomes of the (parity) mapping.

# construct QNN
qnn = SamplerQNN(
    circuit=qc,
    interpret=parity,
    output_shape=output_shape,
    sparse=False,
)

3.2 Configurar el cálculo de la Dimensión Efectiva

Para calcular la dimensión efectiva de nuestra QNN usando la clase EffectiveDimension, necesitamos una serie de conjuntos de muestras y pesos de entrada, así como el número total de muestras de datos disponibles en un conjunto de datos. Las input_samples y weight_samples se establecen en el constructor de la clase, mientras que el número de muestras de datos se proporciona durante la llamada al cálculo de la dimensión efectiva, para poder probar y comparar cómo cambia esta medida con diferentes tamaños de conjuntos de datos.

Podemos definir el número de muestras de entrada y muestras de peso y la clase muestreará aleatoriamente un arreglo correspondiente a una distribución normal (para input_samples) o uniforme (para weight_samples). En lugar de pasar una cantidad de muestras, podemos pasar un arreglo, muestreado manualmente.

# we can set the total number of input samples and weight samples for random selection
num_input_samples = 10
num_weight_samples = 10

global_ed = EffectiveDimension(
    qnn=qnn, weight_samples=num_weight_samples, input_samples=num_input_samples
)

Si queremos probar un conjunto específico de muestras de entrada y muestras de peso, podemos proporcionarlo directamente a la clase EffectiveDimension como se muestra en el siguiente fragmento de código:

# we can also provide user-defined samples and parameters
input_samples = algorithm_globals.random.normal(0, 1, size=(10, qnn.num_inputs))
weight_samples = algorithm_globals.random.uniform(0, 1, size=(10, qnn.num_weights))

global_ed = EffectiveDimension(qnn=qnn, weight_samples=weight_samples, input_samples=input_samples)

El algoritmo de dimensión efectiva también requiere un tamaño de conjunto de datos. En este ejemplo, definiremos un arreglo de tamaños para luego ver cómo esta entrada afecta el resultado.

# finally, we will define ranges to test different numbers of data, n
n = [5000, 8000, 10000, 40000, 60000, 100000, 150000, 200000, 500000, 1000000]

3.3 Calcular la Dimensión Efectiva Global

Ahora calculemos la dimensión efectiva de nuestra red para el conjunto previamente definido de muestras de entrada, pesos y un tamaño de conjunto de datos de 5000.

global_eff_dim_0 = global_ed.get_effective_dimension(dataset_size=n[0])

Los valores efectivos de dimensión oscilarán entre 0 y d, donde d representa la dimensión del modelo, y se obtiene prácticamente a partir del número de pesos de la QNN. Al dividir el resultado entre d, podemos obtener la dimensión efectiva normalizada, que se correlaciona directamente con la capacidad del modelo.

d = qnn.num_weights

print("Data size: {}, global effective dimension: {:.4f}".format(n[0], global_eff_dim_0))
print(
    "Number of weights: {}, normalized effective dimension: {:.4f}".format(d, global_eff_dim_0 / d)
)

Data size: 5000, global effective dimension: 4.6657
Number of weights: 6, normalized effective dimension: 0.7776

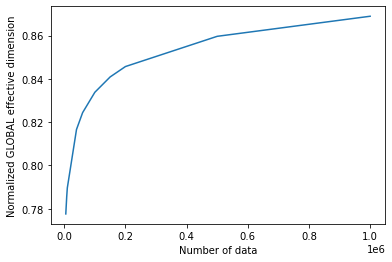
Al llamar a la clase EffectiveDimension con un arreglo de tamaños de entrada n, podemos monitorear cómo cambia la dimensión efectiva con el tamaño del conjunto de datos.

global_eff_dim_1 = global_ed.get_effective_dimension(dataset_size=n)

print("Effective dimension: {}".format(global_eff_dim_1))
print("Number of weights: {}".format(d))

Effective dimension: [4.66565096 4.7133723  4.73782922 4.89963559 4.94632272 5.00280009
 5.04530433 5.07408394 5.15786005 5.21349874]
Number of weights: 6

# plot the normalized effective dimension for the model
plt.plot(n, np.array(global_eff_dim_1) / d)
plt.xlabel("Number of data")
plt.ylabel("Normalized GLOBAL effective dimension")
plt.show()

4. Ejemplo de Dimensión Efectiva Local

Como se explicó en la introducción, el algoritmo de dimensión efectiva local solo usa un conjunto de pesos y se puede usar para monitorear cómo el entrenamiento afecta la expresividad de una red neuronal. La clase LocalEffectiveDimension impone esta restricción para garantizar que estos cálculos sean conceptualmente independientes, pero el resto de la implementación se comparte con EffectiveDimension.

Este ejemplo muestra cómo aprovechar la clase LocalEffectiveDimension para analizar el efecto del entrenamiento en la expresividad de la QNN.

4.1 Definir el Conjunto de Datos y la QNN

Comenzamos creando un conjunto de datos de clasificación binaria 3D utilizando la función make_classification de scikit-learn.

num_inputs = 3
num_samples = 50

X, y = make_classification(
    n_samples=num_samples,
    n_features=num_inputs,
    n_informative=3,
    n_redundant=0,
    n_clusters_per_class=1,
    class_sep=2.0,
)
X = MinMaxScaler().fit_transform(X)
y = 2 * y - 1  # labels in {-1, 1}

El siguiente paso es crear una QNN, una instancia de EstimatorQNN en nuestro caso de la misma manera que creamos una instancia de SamplerQNN.

estimator_qnn = EstimatorQNN(circuit=qc)

4.2 Entrenar la QNN

Ahora podemos proceder a entrenar la QNN. El paso de entrenamiento puede tomar algún tiempo, sé paciente. Puedes pasar una devolución de llamada al clasificador para observar cómo se desarrolla el proceso de entrenamiento. Fijamos initial_point con fines de reproducibilidad, como de costumbre.

# callback function that draws a live plot when the .fit() method is called
def callback_graph(weights, obj_func_eval):
    clear_output(wait=True)
    objective_func_vals.append(obj_func_eval)
    plt.title("Objective function value against iteration")
    plt.xlabel("Iteration")
    plt.ylabel("Objective function value")
    plt.plot(range(len(objective_func_vals)), objective_func_vals)
    plt.show()

# construct classifier
initial_point = algorithm_globals.random.random(estimator_qnn.num_weights)

estimator_classifier = NeuralNetworkClassifier(
    neural_network=estimator_qnn,
    optimizer=COBYLA(maxiter=80),
    initial_point=initial_point,
    callback=callback_graph,
)

# create empty array for callback to store evaluations of the objective function (callback)
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)

# fit classifier to data
estimator_classifier.fit(X, y)

# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)

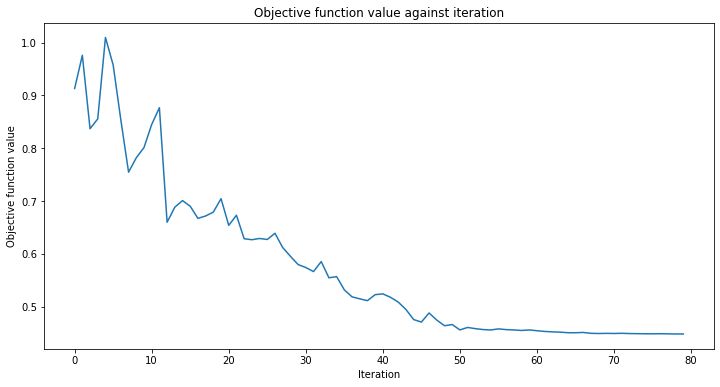
El clasificador ahora puede diferenciar entre clases con una precisión de:

# score classifier
estimator_classifier.score(X, y)

0.96

4.3 Calcular la Dimensión Efectiva Local de QNN entrenadas

Ahora que hemos entrenado nuestra red, evaluemos la dimensión efectiva local en función de los pesos entrenados. Para ello accedemos a los pesos entrenados directamente desde el clasificador.

trained_weights = estimator_classifier.weights

# get Local Effective Dimension for set of trained weights
local_ed_trained = LocalEffectiveDimension(
    qnn=estimator_qnn, weight_samples=trained_weights, input_samples=X
)

local_eff_dim_trained = local_ed_trained.get_effective_dimension(dataset_size=n)

print(
    "normalized local effective dimensions for trained QNN: ",
    local_eff_dim_trained / estimator_qnn.num_weights,
)

normalized local effective dimensions for trained QNN:  [0.38001027 0.38667693 0.39017714 0.41507888 0.42307677 0.43341398
 0.44170977 0.44758111 0.46577231 0.4786767 ]

4.4 Calcular la Dimensión Efectiva Local de QNN no entrenadas

Podemos comparar este resultado con la dimensión efectiva de la red no entrenada, usando el initial_point como nuestra muestra de peso:

# get Local Effective Dimension for set of untrained weights
local_ed_untrained = LocalEffectiveDimension(
    qnn=estimator_qnn, weight_samples=initial_point, input_samples=X
)

local_eff_dim_untrained = local_ed_untrained.get_effective_dimension(dataset_size=n)

print(
    "normalized local effective dimensions for untrained QNN: ",
    local_eff_dim_untrained / estimator_qnn.num_weights,
)

normalized local effective dimensions for untrained QNN:  [0.69803061 0.7130991  0.7203237  0.76321615 0.77452215 0.7877625
 0.79746712 0.8039319  0.82236146 0.83435907]

4.5 Graficar y analizar resultados

Si graficamos los valores de las dimensiones efectivas antes y después del entrenamiento, podemos ver el siguiente resultado:

# plot the normalized effective dimension for the model
plt.plot(n, np.array(local_eff_dim_trained) / estimator_qnn.num_weights, label="trained weights")
plt.plot(
    n, np.array(local_eff_dim_untrained) / estimator_qnn.num_weights, label="untrained weights"
)

plt.xlabel("Number of data")
plt.ylabel("Normalized LOCAL effective dimension")
plt.legend()
plt.show()

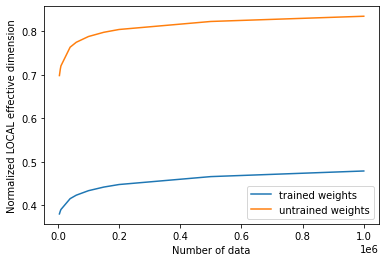
En general, deberíamos esperar que el valor de la dimensión efectiva local disminuya después del entrenamiento. Esto se puede entender mirando hacia atrás en el objetivo principal del machine learning, que es elegir un modelo que sea lo suficientemente expresivo como para ajustarse a tus datos, pero no demasiado expresivo como para que se sobreajuste y funcione mal en nuevas muestras de datos.

Ciertos optimizadores ayudan a regularizar el sobreajuste de un modelo mediante el aprendizaje de parámetros, y esta acción de aprendizaje reduce inherentemente la expresividad de un modelo, medida por la dimensión efectiva local. Siguiendo esta lógica, lo más probable es que un conjunto de parámetros inicializados aleatoriamente produzca una dimensión efectiva más alta que el conjunto final de pesos entrenados, porque ese modelo con esa parametrización particular está “usando más parámetros” innecesariamente para ajustar los datos. Después del entrenamiento (con la regularización implícita), un modelo entrenado no necesitará usar tantos parámetros y, por lo tanto, tendrá más “parámetros inactivos” y una dimensión efectiva menor.

Sin embargo, debemos tener en cuenta que esta es la intuición general, y puede haber casos en los que un conjunto de pesos seleccionados al azar proporcione una dimensión efectiva más baja que los pesos entrenados para un modelo específico.

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
qiskit-terra	0.24.0
qiskit-aer	0.12.0
qiskit-ignis	0.6.0
qiskit-ibmq-provider	0.20.2
qiskit	0.43.0
qiskit-machine-learning	0.7.0
System information
Python version	3.8.8
Python compiler	Clang 10.0.0
Python build	default, Apr 13 2021 12:59:45
OS	Darwin
CPUs	8
Memory (Gb)	32.0
Tue Jun 13 16:40:08 2023 CEST

This code is a part of Qiskit

© Copyright IBM 2017, 2023.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.