Note

This is the documentation for the current state of the development branch of Qiskit Experiments. The documentation or APIs here can change prior to being released.

Quantum Volume

Quantum Volume (QV) is a single-number metric that can be measured using a concrete protocol on near-term quantum computers of modest size. The QV method quantifies the largest random circuit of equal width and depth that the computer successfully implements. Quantum computing systems with high-fidelity operations, high connectivity, large calibrated gate sets, and circuit rewriting toolchains are expected to have higher quantum volumes. See the Qiskit Textbook for an explanation on the QV method, which is described in Refs. [1] [2].

The Quantum Volume is determined by the largest successful circuit depth $d_{max}$, and equals to $2^{d_{max}}$. In this experiment, we generate QV circuits using the qiskit.circuit.library.QuantumVolume class on $d$ qubits, which contain $d$ layers, where each layer consists of random 2-qubit unitary gates from $SU(4)$, followed by a random permutation on the $d$ qubit. Then these circuits run on the quantum backend and on an ideal simulator (either qiskit_aer.AerSimulator or qiskit.quantum_info.Statevector).

A depth $d$ QV circuit is successful if it has mean heavy-output probability > 2/3 with confidence level > 0.977 (corresponding to z_value = 2), and at least 100 trials have been ran.

Note

This tutorial requires the qiskit-aer package to run simulations. You can install it with python -m pip install qiskit-aer.

from qiskit_experiments.framework import BatchExperiment
from qiskit_experiments.library import QuantumVolume

# For simulation
from qiskit_aer import AerSimulator
from qiskit_aer.noise import NoiseModel, depolarizing_error

noise_model = NoiseModel()
noise_model.add_all_qubit_quantum_error(depolarizing_error(5e-4, 1), ["sx", "x"])
noise_model.add_all_qubit_quantum_error(depolarizing_error(0, 1), ["rz"])
noise_model.add_all_qubit_quantum_error(depolarizing_error(1e-2, 2), ["cx"])
backend = AerSimulator(noise_model=noise_model, seed_simulator=42)

QV experiment

To run the QV experiment we need need to provide the following QV parameters, in order to generate the QV circuits and run them on a backend and on an ideal simulator:

• qubits: The number of qubits or list of physical qubits for the experiment.

• trials: The number of trials to run the quantum volume circuit (the default is 100).

• seed: Seed or generator object for random number generation. If None then default_rng will be used.

• simulation_backend: The simulator backend to use to generate the expected results. the simulator must have a save_probabilities method. If None, AerSimulator will be used (in case AerSimulator is not installed, Statevector will be used).

Note: In some cases, 100 trials are not enough to obtain a QV greater than 1 for the specified number of qubits. In this case, adding more trials may reduce the error bars to allow passing the threshold.

The analysis results of the QV Experiment are:

• The mean heavy-output probabilities (HOP) and standard deviation

• The calculated quantum volume, which will be 1 if the experiment does not pass the threshold

Extra data included in the analysis results includes

• The heavy HOPs for each trial

• Confidence level (should be greater than 0.977)

• The number of trials and depth of the QV circuits

• Whether the QV circuit was successful

qubits = tuple(range(4)) # Can use specific qubits. for example [2, 4, 7, 10]

qv_exp = QuantumVolume(qubits, seed=42)
# Transpile options like optimization_level affect only the real device run and not the simulation run
# Run options affect both simulation and real device runs
qv_exp.set_transpile_options(optimization_level=3)

# Run experiment
expdata = qv_exp.run(backend).block_for_results()

# View result data
display(expdata.figure(0))

display(expdata.analysis_results(dataframe=True))

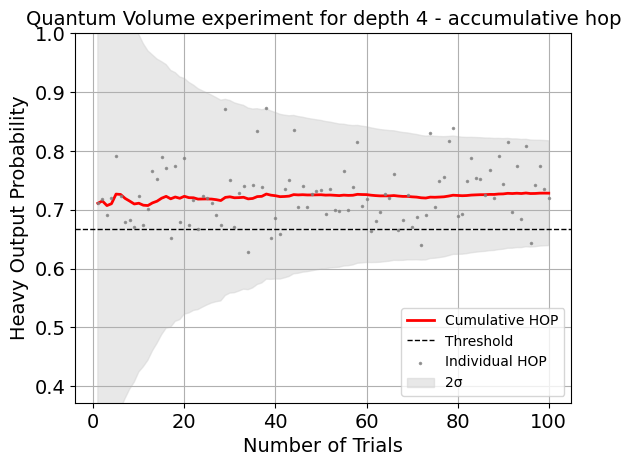
	name	experiment	components	value	quality	backend	run_time	HOPs	two_sigma	depth	trials	success	confidence
eb77518c	mean_HOP	QuantumVolume	[Q0, Q1, Q2, Q3]	0.79+/-0.04	good	aer_simulator	None	[0.7197265625, 0.7373046875, 0.830078125, 0.76...	0.080931	4	100	None	None
17ae2b85	quantum_volume	QuantumVolume	[Q0, Q1, Q2, Q3]	16	good	aer_simulator	None	None	None	4	100	True	0.999153

Adding trials

Adding more trials may reduce the error bars to allow passing the threshold (beside the error bars - QV experiment must have at least 100 trials to be considered successful). In case you want to add less than 100 additional trials, you can modify the amount of trials added before re-running the experiment.

qv_exp.set_experiment_options(trials=10)
expdata2 = qv_exp.run(backend, analysis=None).block_for_results()
expdata2.add_data(expdata.data())
qv_exp.analysis.run(expdata2).block_for_results()

# View result data
display(expdata2.figure(0))
display(expdata2.analysis_results(dataframe=True))

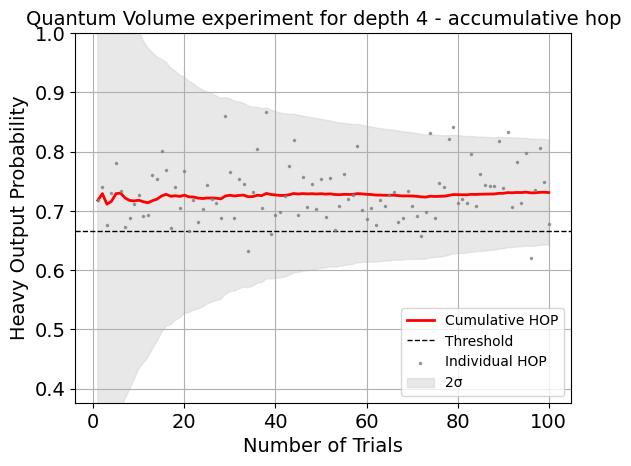
	name	experiment	components	value	quality	backend	run_time	HOPs	two_sigma	depth	trials	success	confidence
af87f868	mean_HOP	QuantumVolume	[Q0, Q1, Q2, Q3]	0.79+/-0.04	good	aer_simulator	None	[0.7197265625, 0.7373046875, 0.830078125, 0.76...	0.077156	4	110	None	None
f2332ff9	quantum_volume	QuantumVolume	[Q0, Q1, Q2, Q3]	16	good	aer_simulator	None	None	None	4	110	True	0.999506

Calculating Quantum Volume using a batch experiment

Run the QV experiment with an increasing number of qubits to check what is the maximum Quantum Volume for the specific device. To reach the real system’s Quantum Volume, one must run more trials and additional enhancements might be required (See Ref. [2] for details).

exps = [QuantumVolume(tuple(range(i))) for i in range(3, 5)]

batch_exp = BatchExperiment(exps)
batch_exp.set_transpile_options(optimization_level=3)

# Run
batch_expdata = batch_exp.run(backend).block_for_results()

Extracting the maximum Quantum Volume.

qv_values = batch_expdata.analysis_results("quantum_volume", dataframe=True).value.tolist()

print(f"Max quantum volume is: {max(qv_values)}")

Max quantum volume is: 16

for i in range(batch_exp.num_experiments):
    print(f"\nComponent experiment {i}")
    display(batch_expdata.figure(i))
display(batch_expdata.analysis_results(dataframe=True))

Component experiment 0

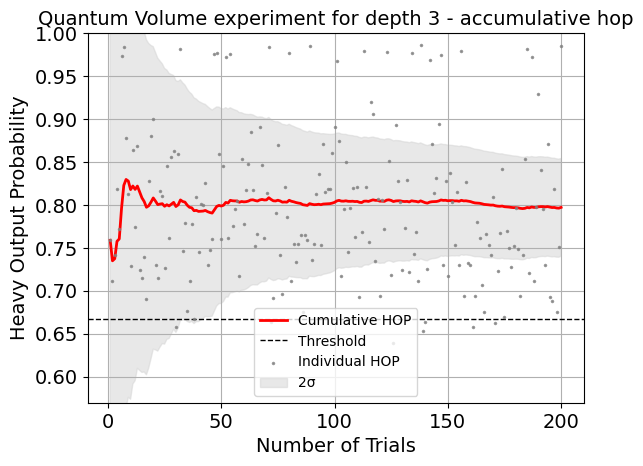
Component experiment 1

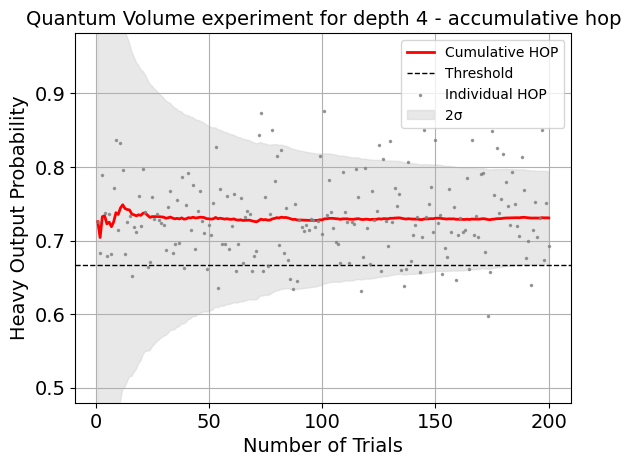
	name	experiment	components	value	quality	backend	run_time	HOPs	two_sigma	depth	trials	success	confidence
bcefbcf7	mean_HOP	QuantumVolume	[Q0, Q1, Q2]	0.83+/-0.04	good	aer_simulator	None	[0.859375, 0.8046875, 0.83984375, 0.853515625,...	0.075565	3	100	None	None
b979fcfc	quantum_volume	QuantumVolume	[Q0, Q1, Q2]	8	good	aer_simulator	None	None	None	3	100	True	0.99999
f8792740	mean_HOP	QuantumVolume	[Q0, Q1, Q2, Q3]	0.80+/-0.04	good	aer_simulator	None	[0.7685546875, 0.7646484375, 0.8115234375, 0.8...	0.079968	4	100	None	None
9336fb63	quantum_volume	QuantumVolume	[Q0, Q1, Q2, Q3]	16	good	aer_simulator	None	None	None	4	100	True	0.999581

References

[1]

Andrew W. Cross, Lev S. Bishop, Sarah Sheldon, Paul D. Nation, and Jay M. Gambetta, Validating quantum computers using randomized model circuits, Phys. Rev. A 100, 032328 (2019). https://arxiv.org/pdf/1811.12926

[2] (1,2)

Petar Jurcevic et. al. Demonstration of quantum volume 64 on a superconducting quantum computing system, https://arxiv.org/pdf/2008.08571

See also

• API documentation: quantum_volume

• Qiskit Textbook: Measuring Quantum Volume