Note

This is the documentation for the current state of the development branch of Qiskit Experiments. The documentation or APIs here can change prior to being released.

Tφ Characterization

\(T_\varphi\), or \(1/\Gamma_\varphi\), is the pure dephasing time of depolarization in the \(x - y\) plane of the Bloch sphere. We compute \(\Gamma_\varphi\) by computing \(\Gamma_2\), the transverse relaxation rate, and subtracting \(\Gamma_1\), the longitudinal relaxation rate. It follows that \(\frac{1}{T_\varphi} = \frac{1}{T_2} - \frac{1}{2T_1}\).

We therefore create a composite experiment consisting of a \(T_1\) experiment and a \(T_2\) experiment. Both Ramsey and Hahn echo experiments can be used here, with different effects. The \(T_2^*\) estimate of the Ramsey experiment is sensitive to inhomogeneous broadening, low-frequency fluctuations that vary between experiments due to \(1/f\)-type noise. The \(T_{2}\) estimate from the Hahn echo (defined as \(T_{2E}\) in [1]) is less sensitive to inhomogeneous broadening due to its refocusing pulse, and so it is strictly larger than \(T_2^*\) on a real device. In superconducting qubits, \(T_2^*\) tends to be significantly smaller than \(T_1\), so \(T_2\) is usually used.

From the \(T_1\) and \(T_2\) estimates, we compute the results for \(T_\varphi.\)

Note

This tutorial requires the qiskit-aer and qiskit-ibm-runtime packages to run simulations. You can install them with python -m pip install qiskit-aer qiskit-ibm-runtime.

import numpy as np
import qiskit
from qiskit_experiments.library.characterization import Tphi

# An Aer simulator
from qiskit_aer import AerSimulator
from qiskit_aer.noise import NoiseModel
from qiskit_ibm_runtime.fake_provider import FakePerth

# Create a pure relaxation noise model for AerSimulator
noise_model = NoiseModel.from_backend(
    FakePerth(), thermal_relaxation=True, gate_error=False, readout_error=False
)

# Create a fake backend simulator
backend = AerSimulator.from_backend(FakePerth(), noise_model=noise_model)

# Time intervals to wait before measurement for t1 and t2
delays_t1 = np.arange(1e-6, 300e-6, 10e-6)
delays_t2 = np.arange(1e-6, 50e-6, 2e-6)

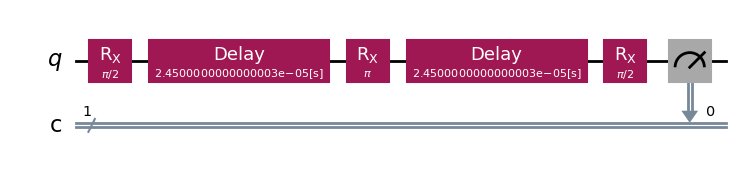
By default, the Tphi experiment will use the Hahn echo experiment for its transverse relaxation time estimate. We can see that the component experiments of the batch Tphi experiment are what we expect for T1 and T2Hahn:

exp = Tphi(physical_qubits=(0,), delays_t1=delays_t1, delays_t2=delays_t2, num_echoes=1)
exp.component_experiment(0).circuits()[-1].draw(output="mpl", style="iqp")
../../_images/tphi_2_0.png 
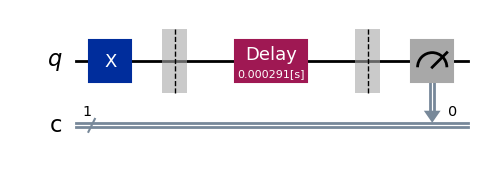
exp.component_experiment(1).circuits()[-1].draw(output="mpl", style="iqp")
../../_images/tphi_3_0.png

Run the experiment and print results:

expdata = exp.run(backend=backend, seed_simulator=100).block_for_results()
result = expdata.analysis_results("T_phi")
print(result)

AnalysisResult
- name: T_phi
- value: -0.0004+/-0.0008
- quality: bad
- extra: <3 items>
- device_components: ['Q0']
- verified: False

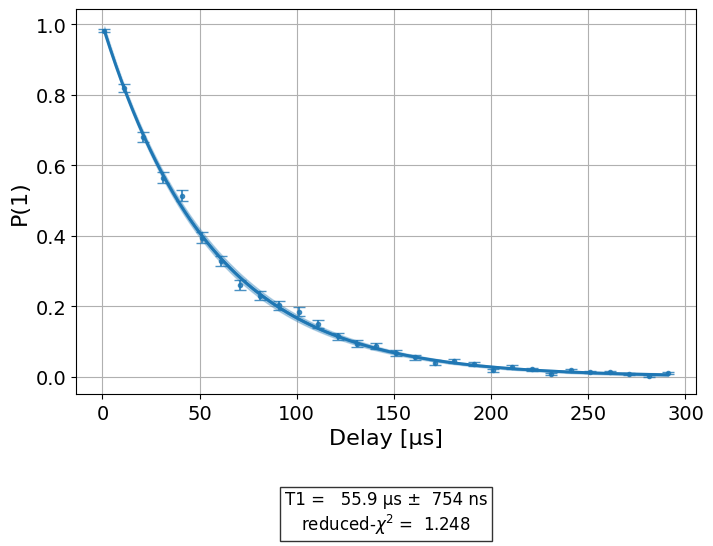
You can also retrieve the results and figures of the constituent experiments. T1:

print(expdata.analysis_results("T1"))
display(expdata.figure(0))

AnalysisResult
- name: T1
- value: (5.59+/-0.08)e-05
- χ²: 1.2479846254534268
- quality: good
- extra: <3 items>
- device_components: ['Q0']
- verified: False
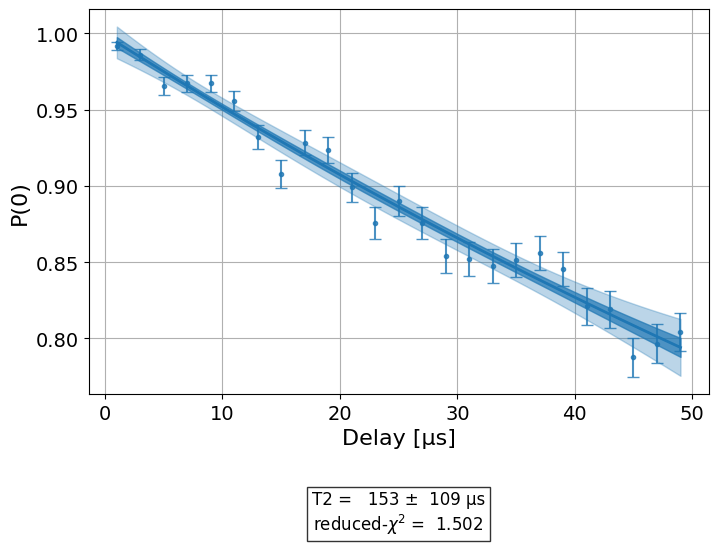
../../_images/tphi_5_1.png

And T2Hahn:

print(expdata.analysis_results("T2"))
display(expdata.figure(1))

AnalysisResult
- name: T2
- value: 0.00015+/-0.00011
- χ²: 1.502092672190198
- quality: bad
- extra: <3 items>
- device_components: ['Q0']
- verified: False
../../_images/tphi_6_1.png

Let’s now run the experiment with T2Ramsey by setting the t2type option to ramsey and specifying osc_freq. Now the second component experiment is a Ramsey experiment:

exp = Tphi(physical_qubits=(0,),
           delays_t1=delays_t1,
           delays_t2=delays_t2,
           t2type="ramsey",
           osc_freq=1e5)

exp.component_experiment(1).circuits()[-1].draw(output="mpl", style="iqp")
../../_images/tphi_7_0.png

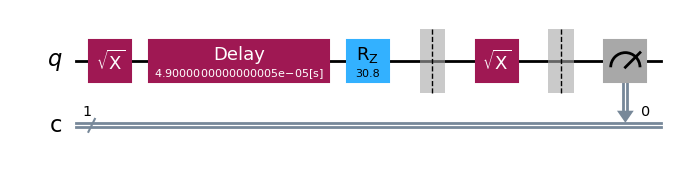
Run and display results:

expdata = exp.run(backend=backend, seed_simulator=100).block_for_results()
print(expdata.analysis_results("T_phi"))
display(expdata.figure(1))

AnalysisResult
- name: T_phi
- value: 0.00053+/-0.00017
- quality: good
- extra: <3 items>
- device_components: ['Q0']
- verified: False
../../_images/tphi_8_1.png

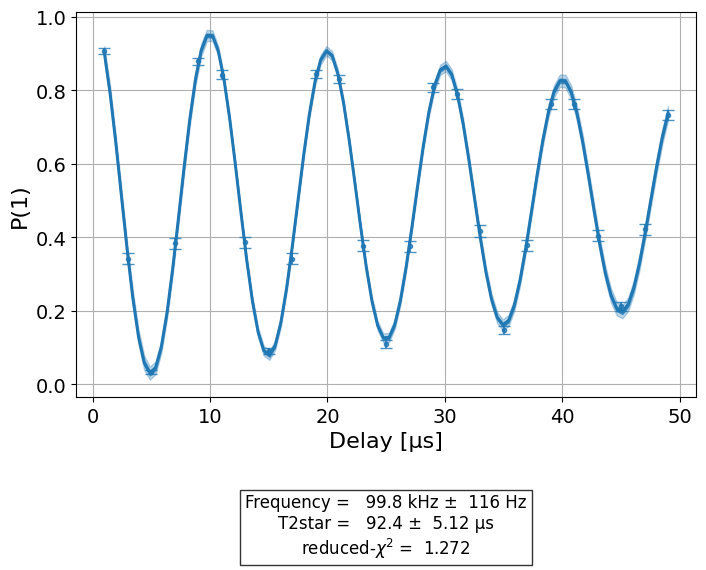
Because we are using a simulator that doesn’t model inhomogeneous broadening, the \(T_2\) and \(T_2^*\) values are not significantly different. On a real superconducting device, \(T_{\varphi}\) should be significantly larger when the Hahn echo experiment is used.

References

See also

  • API documentation: Tphi