Note
This page was generated from docs/tutorials/10_pvqd.ipynb.
Projected Variational Quantum Dynamics#
The projected Variational Quantum Dynamics (p-VQD) algorithm is a quantum algorithm for real time evolution. It’s a variational algorithm that projects the state at time \(t + \Delta_t\), as calculated with Trotterization, onto a parameterized quantum circuit.
For a quantum state \(|\phi(\theta)\rangle = U(\theta)|0\rangle\) constructed by a parameterized quantum circuit \(U(\theta)\) and a Hamiltonian \(H\), the update rule can be written as
\[\theta_{n+1} = \theta_n + \arg\min_{\delta\theta} 1 - |\langle\phi(\theta_n + \delta\theta)|e^{-i\Delta_t H}|\phi(\theta_n)\rangle|^2,\]
where \(e^{-i\Delta_t H}\) is calculated with a Trotter expansion (using e.g. the PauliEvolutionGate in Qiskit!).
The following tutorial explores the p-VQD algorithm, which is available as the PVQD class. For details on the algorithm, see the original paper: Barison et al. Quantum 5, 512 (2021).
The example we’re looking at is the time evolution of the \(|00\rangle\) state under the Hamiltonian
\[H = 0.1 Z_1 Z_2 + X_1 + X_2,\]
which is an Ising Hamiltonian on two neighboring spins, up to a time \(T=1\), where we want to keep track of the total magnetization \(M = Z_1 + Z_2\) as an observable.
[1]:
from qiskit.quantum_info import SparsePauliOp
final_time = 1
hamiltonian = SparsePauliOp.from_sparse_list(
[
("ZZ", [0, 1], 0.1),
("X", [0], 1),
("X", [1], 1),
],
num_qubits=2,
)
observable = SparsePauliOp(["ZI", "IZ"])
After defining our Hamiltonian and observable, we need to choose the parameterized ansatz we project the update steps onto. We have different choices here, but for real time evolution an ansatz that contains building blocks of the evolved Hamiltonian usually performs very well.
[2]:
from qiskit.circuit import QuantumCircuit, ParameterVector
theta = ParameterVector("th", 5)
ansatz = QuantumCircuit(2)
ansatz.rx(theta[0], 0)
ansatz.rx(theta[1], 1)
ansatz.rzz(theta[2], 0, 1)
ansatz.rx(theta[3], 0)
ansatz.rx(theta[4], 1)
# you can try different circuits, like:
# from qiskit.circuit.library import EfficientSU2
# ansatz = EfficientSU2(2, reps=1)
ansatz.draw("mpl", style="clifford")
[2]:
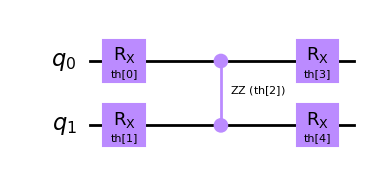
With this ansatz, the \(|00\rangle\) state is prepared if all parameters are 0. Hence we’ll set the initial parameters to \(\theta_0 = 0\):
[3]:
import numpy as np
initial_parameters = np.zeros(ansatz.num_parameters)
Before running the p-VQD algorithm, we need to select the backend and how we want to calculate the expectation values. Here, we’ll perform exact statevector simulations (which are still very fast, as we investigate a 2 qubit system) through the reference primitive implementations found in qiskit.primitives.
[4]:
from qiskit.primitives import Sampler, Estimator
from qiskit_algorithms.state_fidelities import ComputeUncompute
# the fidelity is used to evaluate the objective: the overlap of the variational form and the trotter step
sampler = Sampler()
fidelity = ComputeUncompute(sampler)
# the estimator is used to evaluate the observables
estimator = Estimator()
/tmp/ipykernel_7505/1411506614.py:5: DeprecationWarning: The class ``qiskit.primitives.sampler.Sampler`` is deprecated as of qiskit 1.2. It will be removed no earlier than 3 months after the release date. All implementations of the `BaseSamplerV1` interface have been deprecated in favor of their V2 counterparts. The V2 alternative for the `Sampler` class is `StatevectorSampler`.
sampler = Sampler()
/tmp/ipykernel_7505/1411506614.py:9: DeprecationWarning: The class ``qiskit.primitives.estimator.Estimator`` is deprecated as of qiskit 1.2. It will be removed no earlier than 3 months after the release date. All implementations of the `BaseEstimatorV1` interface have been deprecated in favor of their V2 counterparts. The V2 alternative for the `Estimator` class is `StatevectorEstimator`.
estimator = Estimator()
Since p-VQD performs a classical optimization in each timestep to determine the best parameters for the projection, we also have to specify the classical optimizer. As a first example we’re using BFGS, which typically works well in statevector simulations, but later we can switch to gradient descent.
[5]:
from qiskit_algorithms.optimizers import L_BFGS_B
bfgs = L_BFGS_B()
Now we can define p-VQD and execute it!
[6]:
from qiskit_algorithms import PVQD
pvqd = PVQD(
fidelity, ansatz, initial_parameters, estimator=estimator, num_timesteps=100, optimizer=bfgs
)
The p-VQD implementation follows Qiskit’s time evolution interface, thus we pack all information of the evolution problem into an input class: the hamiltonian under which we evolve the state, the final_time of the evolution and the observables (aux_operators) we keep track of.
[7]:
from qiskit_algorithms import TimeEvolutionProblem
problem = TimeEvolutionProblem(
hamiltonian, time=final_time, aux_operators=[hamiltonian, observable]
)
And then run the algorithm!
[8]:
result = pvqd.evolve(problem)
print(result)
{ 'aux_ops_evaluated': array([ 0.1084508 , -0.82588878]),
'estimated_error': 3.7508893777626895e-06,
'evolved_state': <qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7f2d0b624dc0>,
'fidelities': [ 1.0,
0.9999999966159694,
0.9999999786160764,
0.9999999995406014,
0.9999999996774606,
0.999999996776757,
0.999999990864295,
0.9999999989313226,
0.9999999981647524,
0.9999999971810714,
0.999999995989957,
0.999999994602302,
0.999999999594495,
0.9999999994361006,
0.9999999992124298,
0.9999999989121436,
0.9999999985226362,
0.9999999980299936,
0.9999999974189556,
0.999999996672874,
0.9999999957736904,
0.9999999968119424,
0.9999999961694972,
0.9999999954162004,
0.9999999945370006,
0.9999999935154438,
0.9999999923336444,
0.9999999909722554,
0.9999999905677208,
0.9999999891755638,
0.9999999876113648,
0.9999999858560016,
0.9999999838888428,
0.9999999819005668,
0.999999979760401,
0.999999977696548,
0.9999999752353528,
0.9999999725842242,
0.999999969878108,
0.9999999671203154,
0.9999999640577132,
0.9999999609089124,
0.9999999574907426,
0.9999999537938148,
0.9999999505447132,
0.9999999464730785,
0.9999999420907086,
0.9999999378942585,
0.9999999331205102,
0.999999928835506,
0.9999999239196894,
0.99999991938174,
0.9999999141058752,
0.9999999091800882,
0.9999999036157252,
0.999999898659777,
0.9999998929743918,
0.9999998869819348,
0.9999998822864948,
0.9999998764329812,
0.9999998703034502,
0.9999998652724736,
0.9999998592600384,
0.99999985299987,
0.9999998477712274,
0.9999998415669694,
0.999999836493454,
0.9999998304180336,
0.9999998256516752,
0.9999998197992542,
0.9999999851544044,
0.9999999867881229,
0.999999988021095,
0.999999989113396,
0.999999989805657,
0.9999999898810022,
0.9999999894706822,
0.9999999885138589,
0.9999999869878698,
0.9999999846938158,
0.9999999969813448,
0.9999999952754466,
0.9999999930620576,
0.9999999902635242,
0.9999999868358124,
0.9999999827238916,
0.9999999780439034,
0.9999999724753112,
0.9999999656698108,
0.9999999997478795,
0.9999999995934806,
0.9999999991031044,
0.9999999982450472,
0.9999999971164094,
0.9999999954714566,
0.9999999933490828,
0.9999999909450276,
0.9999999878158726,
0.9999999840840166,
0.9999999800730766,
0.9999999999483394],
'observables': [ array([0.1, 2. ]),
array([0.10012442, 1.99960002]),
array([0.1004976, 1.9984003]),
array([0.10051777, 1.9964013 ]),
array([0.10042778, 1.99360381]),
array([0.10022804, 1.99000892]),
array([0.09991912, 1.98561807]),
array([0.09979579, 1.98042867]),
array([0.09964344, 1.974446 ]),
array([0.09946278, 1.9676725 ]),
array([0.09925462, 1.96011093]),
array([0.09901985, 1.95176437]),
array([0.09898967, 1.94264499]),
array([0.09897178, 1.93274943]),
array([0.09896711, 1.9220818 ]),
array([0.09897664, 1.91064655]),
array([0.09900145, 1.89844844]),
array([0.09904264, 1.88549254]),
array([0.09910136, 1.87178427]),
array([0.09917885, 1.85732931]),
array([0.09927635, 1.84213371]),
array([0.09927761, 1.82618523]),
array([0.09929107, 1.80950716]),
array([0.09931822, 1.79210639]),
array([0.09936062, 1.77399015]),
array([0.09941986, 1.75516595]),
array([0.09949756, 1.73564157]),
array([0.09959536, 1.71542512]),
array([0.09962259, 1.69452542]),
array([0.09966734, 1.67295044]),
array([0.09973141, 1.65070908]),
array([0.09981661, 1.6278105 ]),
array([0.09992478, 1.60426415]),
array([0.1000427 , 1.58005951]),
array([0.10017543, 1.5552472 ]),
array([0.10030531, 1.52979153]),
array([0.10045041, 1.50374947]),
array([0.10061043, 1.47708472]),
array([0.10077635, 1.44986199]),
array([0.10094772, 1.42203083]),
array([0.10112537, 1.39366341]),
array([0.10131134, 1.36471057]),
array([0.10150349, 1.33524436]),
array([0.10171875, 1.30521889]),
array([0.10188619, 1.27467901]),
array([0.10208815, 1.24363382]),
array([0.10232651, 1.21209601]),
array([0.10256015, 1.18005127]),
array([0.10283237, 1.14753891]),
array([0.10309362, 1.11460352]),
array([0.10338214, 1.0811978 ]),
array([0.10364401, 1.04737938]),
array([0.10394712, 1.01314728]),
array([0.10424113, 0.9784913 ]),
array([0.10457806, 0.94344886]),
array([0.10488519, 0.90804359]),
array([0.10523611, 0.87228034]),
array([0.10563222, 0.83617363]),
array([0.1059748 , 0.79973374]),
array([0.10636254, 0.76297924]),
array([0.10679666, 0.725925 ]),
array([0.10719113, 0.68856805]),
array([0.10763215, 0.65094079]),
array([0.10812072, 0.61305842]),
array([0.10858807, 0.57493155]),
array([0.10910327, 0.5365799 ]),
array([0.10959731, 0.4980134 ]),
array([0.11013926, 0.45925279]),
array([0.11065802, 0.42031304]),
array([0.11122443, 0.38121013]),
array([0.11132626, 0.34195989]),
array([0.11141037, 0.30258492]),
array([0.11147636, 0.26307261]),
array([0.11153622, 0.22346446]),
array([0.11157786, 0.18376714]),
array([0.11159901, 0.14399885]),
array([0.11159468, 0.10418261]),
array([0.11156505, 0.06432252]),
array([0.11150566, 0.02445129]),
array([ 0.11140992, -0.01541126]),
array([ 0.1113703, -0.0552832]),
array([ 0.11129021, -0.09510915]),
array([ 0.11118104, -0.13491348]),
array([ 0.11103952, -0.17463681]),
array([ 0.11086372, -0.21430888]),
array([ 0.11065207, -0.25386651]),
array([ 0.11041684, -0.29332569]),
array([ 0.11014218, -0.33267325]),
array([ 0.10979001, -0.37188546]),
array([ 0.10983319, -0.41093901]),
array([ 0.10984365, -0.44982345]),
array([ 0.1098199 , -0.48852319]),
array([ 0.10976047, -0.52702272]),
array([ 0.10968011, -0.56529139]),
array([ 0.10956059, -0.60332912]),
array([ 0.10940037, -0.64112065]),
array([ 0.10921915, -0.6786642 ]),
array([ 0.10899342, -0.71593099]),
array([ 0.10872162, -0.75290609]),
array([ 0.10842847, -0.78955464]),
array([ 0.1084508 , -0.82588878])],
'parameters': [ array([0., 0., 0., 0., 0.]),
array([0.01059261, 0.00982697, 0.00805252, 0.00940747, 0.01017311]),
array([0.02118523, 0.01965394, 0.01610504, 0.01881493, 0.02034623]),
array([0.02994049, 0.02780753, 0.01520124, 0.03005935, 0.03219237]),
array([0.03869574, 0.03596112, 0.01429743, 0.04130377, 0.04403852]),
array([0.047451 , 0.04411471, 0.01339363, 0.05254819, 0.05588467]),
array([0.05620626, 0.0522683 , 0.01248983, 0.06379261, 0.06773081]),
array([0.06507739, 0.06053761, 0.01391548, 0.07493994, 0.07947561]),
array([0.07394852, 0.06880692, 0.01534113, 0.08608727, 0.09122041]),
array([0.08281965, 0.07707622, 0.01676678, 0.0972346 , 0.10296521]),
array([0.09169077, 0.08534553, 0.01819243, 0.10838193, 0.11471001]),
array([0.1005619 , 0.09361484, 0.01961808, 0.11952926, 0.12645481]),
array([0.10947117, 0.10193866, 0.02212797, 0.13061861, 0.13813087]),
array([0.11838043, 0.11026248, 0.02463786, 0.14170796, 0.14980694]),
array([0.1272897 , 0.1185863 , 0.02714776, 0.15279731, 0.16148301]),
array([0.13619897, 0.12691013, 0.02965765, 0.16388665, 0.17315908]),
array([0.14510823, 0.13523395, 0.03216754, 0.174976 , 0.18483515]),
array([0.1540175 , 0.14355777, 0.03467743, 0.18606535, 0.19651122]),
array([0.16292676, 0.15188159, 0.03718733, 0.1971547 , 0.20818728]),
array([0.17183603, 0.16020542, 0.03969722, 0.20824405, 0.21986335]),
array([0.1807453 , 0.16852924, 0.04220711, 0.2193334 , 0.23153942]),
array([0.18964028, 0.17685769, 0.04439444, 0.23045908, 0.24323133]),
array([0.19853527, 0.18518613, 0.04658176, 0.24158477, 0.25492323]),
array([0.20743025, 0.19351458, 0.04876909, 0.25271045, 0.26661514]),
array([0.21632524, 0.20184303, 0.05095642, 0.26383613, 0.27830704]),
array([0.22522022, 0.21017148, 0.05314374, 0.27496181, 0.28999895]),
array([0.23411521, 0.21849992, 0.05533107, 0.28608749, 0.30169086]),
array([0.24301019, 0.22682837, 0.0575184 , 0.29721317, 0.31338276]),
array([0.25188934, 0.23516091, 0.05950933, 0.30835229, 0.32506881]),
array([0.2607685 , 0.24349345, 0.06150027, 0.3194914 , 0.33675486]),
array([0.26964765, 0.25182599, 0.06349121, 0.33063052, 0.3484409 ]),
array([0.2785268 , 0.26015852, 0.06548214, 0.34176963, 0.36012695]),
array([0.28740595, 0.26849106, 0.06747308, 0.35290874, 0.371813 ]),
array([0.29629112, 0.27683435, 0.06943732, 0.36405699, 0.38350556]),
array([0.30516704, 0.28517007, 0.07138037, 0.37519831, 0.39518708]),
array([0.31404935, 0.29352026, 0.07327196, 0.38635108, 0.4068745 ]),
array([0.32292265, 0.30186357, 0.07514111, 0.39749678, 0.41855029]),
array([0.33180385, 0.31021905, 0.07698804, 0.40865207, 0.43023386]),
array([0.34067345, 0.31856668, 0.07879378, 0.41979864, 0.4419018 ]),
array([0.34955281, 0.32693144, 0.08055985, 0.43095698, 0.45357747]),
array([0.35842182, 0.33529025, 0.08228443, 0.44210657, 0.46523675]),
array([0.36730077, 0.34366667, 0.08397256, 0.45326655, 0.47690217]),
array([0.37617062, 0.3520391 , 0.08561791, 0.46441747, 0.48854999]),
array([0.38504976, 0.36042518, 0.08724751, 0.47557726, 0.50020568]),
array([0.39393057, 0.3688366 , 0.08875295, 0.48673102, 0.51183122]),
array([0.40281138, 0.37724801, 0.09025839, 0.49788478, 0.52345676]),
array([0.4116922 , 0.38565942, 0.09176383, 0.50903854, 0.5350823 ]),
array([0.42058384, 0.39409216, 0.09320943, 0.52019683, 0.54670212]),
array([0.42947547, 0.4025249 , 0.09465504, 0.53135511, 0.55832194]),
array([0.43836175, 0.41096431, 0.09602961, 0.54249807, 0.56991446]),
array([0.44725895, 0.41941865, 0.09738694, 0.55364746, 0.58150956]),
array([0.45616184, 0.42789743, 0.09865214, 0.56477991, 0.59306912]),
array([0.46506473, 0.4363762 , 0.09991735, 0.57591235, 0.60462867]),
array([0.47398751, 0.44489238, 0.10111404, 0.58703661, 0.6161629 ]),
array([0.4829103 , 0.45340856, 0.10231073, 0.59816088, 0.62769712]),
array([0.49185056, 0.46196484, 0.10341135, 0.60925938, 0.63918308]),
array([0.50079082, 0.47052112, 0.10451198, 0.62035789, 0.65066905]),
array([0.50973108, 0.47907741, 0.1056126 , 0.6314564 , 0.66215501]),
array([0.51870979, 0.48770397, 0.10658725, 0.64251444, 0.67356893]),
array([0.5276885 , 0.49633053, 0.1075619 , 0.65357249, 0.68498286]),
array([0.53666722, 0.50495708, 0.10853655, 0.66463054, 0.69639679]),
array([0.54568154, 0.51364123, 0.10940589, 0.67565837, 0.70775912]),
array([0.55469586, 0.52232538, 0.11027522, 0.68668619, 0.71912146]),
array([0.56371018, 0.53100952, 0.11114456, 0.69771401, 0.73048379]),
array([0.5727449 , 0.53972618, 0.11193319, 0.70872039, 0.74181307]),
array([0.58177962, 0.54844284, 0.11272182, 0.71972677, 0.75314235]),
array([0.59083987, 0.55719732, 0.11343062, 0.73070744, 0.76443291]),
array([0.59990011, 0.56595179, 0.11413943, 0.74168812, 0.77572348]),
array([0.60898978, 0.57475209, 0.11476708, 0.75263365, 0.78696731]),
array([0.61807945, 0.58355238, 0.11539473, 0.76357919, 0.79821115]),
array([0.63636375, 0.60445446, 0.11460409, 0.76527467, 0.79729823]),
array([0.65466757, 0.62534291, 0.11391095, 0.76694893, 0.79639457]),
array([0.67299407, 0.64622675, 0.11330944, 0.76861016, 0.7955086 ]),
array([0.69135237, 0.66708295, 0.11280726, 0.7702394 , 0.79464846]),
array([0.70974397, 0.68790892, 0.11238813, 0.77183824, 0.7938219 ]),
array([0.72815708, 0.70871272, 0.11204665, 0.7734175 , 0.79301943]),
array([0.74658655, 0.72949237, 0.11177537, 0.7749796 , 0.79223834]),
array([0.76503349, 0.75024758, 0.11157264, 0.77652771, 0.7914868 ]),
array([0.78349023, 0.77097566, 0.11143256, 0.77806363, 0.79075635]),
array([0.80195069, 0.7916839 , 0.11134758, 0.77959233, 0.79003647]),
array([0.82071932, 0.8098314 , 0.11139455, 0.78083058, 0.79189043]),
array([0.83947476, 0.82797728, 0.11147314, 0.78206457, 0.79374412]),
array([0.85823432, 0.84612338, 0.11159515, 0.78331376, 0.795601 ]),
array([0.87697793, 0.86426612, 0.11175797, 0.78455975, 0.79745943]),
array([0.89572489, 0.88240724, 0.11196049, 0.78582381, 0.79932318]),
array([0.91445306, 0.90054281, 0.11220214, 0.78708615, 0.8011906 ]),
array([0.93316435, 0.91866646, 0.11249634, 0.78837489, 0.80307217]),
array([0.95186178, 0.93677948, 0.11282831, 0.78968731, 0.80496743]),
array([0.97055922, 0.95489251, 0.11316027, 0.79099974, 0.80686269]),
array([0.98527971, 0.97005378, 0.11368141, 0.79630271, 0.81172271]),
array([1.00000021, 0.98521506, 0.11420255, 0.80160569, 0.81658272]),
array([1.0147207 , 1.00037633, 0.11472369, 0.80690866, 0.82144274]),
array([1.0294412 , 1.0155376 , 0.11524483, 0.81221163, 0.82630275]),
array([1.04415449, 1.03069389, 0.11578418, 0.81751071, 0.83116571]),
array([1.05886779, 1.04585019, 0.11632352, 0.82280979, 0.83602866]),
array([1.07358108, 1.06100648, 0.11686286, 0.82810887, 0.84089162]),
array([1.08829621, 1.0761575 , 0.11742684, 0.83341964, 0.84576466]),
array([1.10301134, 1.09130853, 0.11799082, 0.8387304 , 0.85063771]),
array([1.11772647, 1.10645955, 0.1185548 , 0.84404117, 0.85551075]),
array([1.1324215 , 1.12159267, 0.11914978, 0.8493574 , 0.86039995]),
array([1.14520263, 1.13427221, 0.11977574, 0.85660193, 0.86775092])],
'times': [ 0.0,
0.01,
0.02,
0.03,
0.04,
0.05,
0.06,
0.07,
0.08,
0.09,
0.1,
0.11,
0.12,
0.13,
0.14,
0.15,
0.16,
0.17,
0.18,
0.19,
0.2,
0.21,
0.22,
0.23,
0.24,
0.25,
0.26,
0.27,
0.28,
0.29,
0.3,
0.31,
0.32,
0.33,
0.34,
0.35000000000000003,
0.36,
0.37,
0.38,
0.39,
0.4,
0.41000000000000003,
0.42,
0.43,
0.44,
0.45,
0.46,
0.47000000000000003,
0.48,
0.49,
0.5,
0.51,
0.52,
0.53,
0.54,
0.55,
0.56,
0.5700000000000001,
0.58,
0.59,
0.6,
0.61,
0.62,
0.63,
0.64,
0.65,
0.66,
0.67,
0.68,
0.6900000000000001,
0.7000000000000001,
0.71,
0.72,
0.73,
0.74,
0.75,
0.76,
0.77,
0.78,
0.79,
0.8,
0.81,
0.8200000000000001,
0.8300000000000001,
0.84,
0.85,
0.86,
0.87,
0.88,
0.89,
0.9,
0.91,
0.92,
0.93,
0.9400000000000001,
0.9500000000000001,
0.96,
0.97,
0.98,
0.99,
1.0]}
Now we can have a look at the results, which are stored in a PVQDResult object. This class has the fields
evolved_state: The quantum circuit with the parameters at the final evolution time.times: The timesteps of the time integration. At these times we have the parameter values and evaluated the observables.parameters: The parameter values at each timestep.observables: The observable values at each timestep.fidelities: The fidelity of projecting the Trotter timestep onto the variational form at each timestep.estimated_error: The estimated error as product of all fidelities.
The energy should be constant in a real time evolution. However, we are projecting the time-evolved state onto a variational form, which might violate this rule. Ideally the energy is still more or less constant. In this evolution here we observe shifts of ~5% of the energy.
[9]:
import matplotlib.pyplot as plt
energies = np.real(result.observables)[:, 0]
plt.plot(result.times, energies, color="royalblue")
plt.xlabel("time $t$")
plt.ylabel("energy $E$")
plt.title("Energy over time")
[9]:
Text(0.5, 1.0, 'Energy over time')
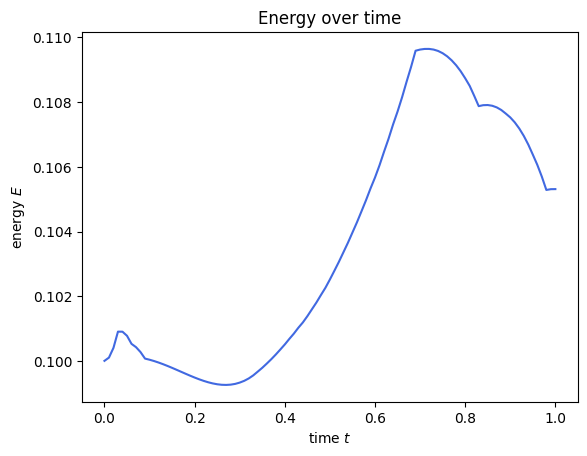
Since we also kept track of the total magnetization of the system, we can plot that quantity too. However let’s first compute exact reference values to verify our algorithm results.
[10]:
import scipy as sc
def exact(final_time, timestep, hamiltonian, initial_state):
"""Get the exact values for energy and the observable."""
O = observable.to_matrix()
H = hamiltonian.to_matrix()
energ, magn = [], [] # list of energies and magnetizations evaluated at timesteps timestep
times = [] # list of timepoints at which energy/obs are evaluated
time = 0
while time <= final_time:
# get exact state at time t
exact_state = initial_state.evolve(sc.linalg.expm(-1j * time * H))
# store observables and time
times.append(time)
energ.append(exact_state.expectation_value(H).real)
magn.append(exact_state.expectation_value(observable).real)
# next timestep
time += timestep
return times, energ, magn
[11]:
from qiskit.quantum_info import Statevector
initial_state = Statevector(ansatz.assign_parameters(initial_parameters))
exact_times, exact_energies, exact_magnetizations = exact(
final_time, 0.01, hamiltonian, initial_state
)
[12]:
magnetizations = np.real(result.observables)[:, 1]
plt.plot(result.times, magnetizations.real, color="crimson", label="PVQD")
plt.plot(exact_times, exact_magnetizations, ":", color="k", label="Exact")
plt.xlabel("time $t$")
plt.ylabel(r"magnetization $\langle Z_1 Z_2 \rangle$")
plt.title("Magnetization over time")
plt.legend(loc="best")
[12]:
<matplotlib.legend.Legend at 0x7f2d0c272550>
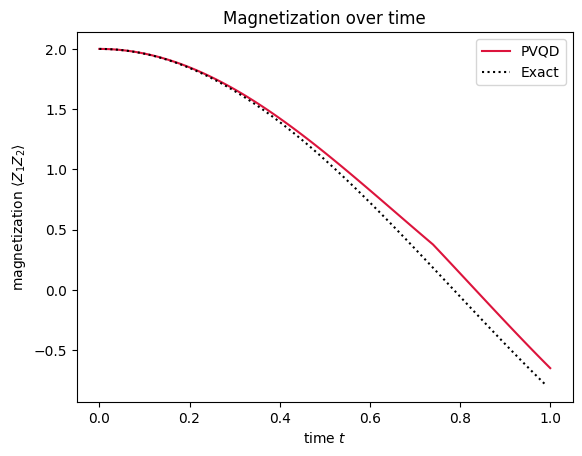
Looks pretty good!
Gradient-based optimizations#
The PVQD class also implements parameter-shift gradients for the loss function and we can use a gradient descent optimization routine
\[\theta_{k+1} = \theta_{k} - \eta_k \nabla\ell(\theta_k).\]
Here we’re using a learning rate of
\[\eta_k = 0.1 k^{-0.602}\]
and 80 optimization steps in each timestep.
[13]:
from qiskit_algorithms.optimizers import GradientDescent
maxiter = 80
learning_rate = 0.1 * np.arange(1, maxiter + 1) ** (-0.602)
gd = GradientDescent(maxiter, lambda: iter(learning_rate))
[14]:
pvqd.optimizer = gd
The following cell would take a few minutes to run for 100 timesteps, so we reduce them here.
[15]:
n = 10
pvqd.num_timesteps = n
problem.time = 0.1
[16]:
result_gd = pvqd.evolve(problem)
[17]:
energies_gd = np.real(result_gd.observables)[:, 0]
plt.plot(result.times[: n + 1], energies[: n + 1], "-", color="royalblue", label="BFGS")
plt.plot(result_gd.times, energies_gd, "--", color="royalblue", label="Gradient descent")
plt.plot(exact_times[: n + 1], exact_energies[: n + 1], ":", color="k", label="Exact")
plt.legend(loc="best")
plt.xlabel("time $t$")
plt.ylabel("energy $E$")
plt.title("Energy over time")
[17]:
Text(0.5, 1.0, 'Energy over time')
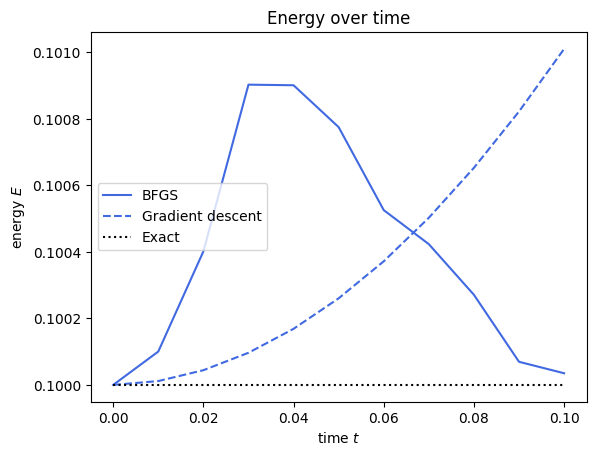
We can observe here, that the energy does vary quite a bit! But as we mentioned before, p-VQD does not preserve the energy.
[18]:
magnetizations_gd = np.real(result_gd.observables)[:, 1]
plt.plot(result.times[: n + 1], magnetizations[: n + 1], "-", color="crimson", label="BFGS")
plt.plot(result_gd.times, magnetizations_gd, "--", color="crimson", label="Gradient descent")
plt.plot(exact_times[: n + 1], exact_magnetizations[: n + 1], ":", color="k", label="Exact")
plt.legend(loc="best")
plt.xlabel("time $t$")
plt.ylabel(r"magnetization $\langle Z_1 + Z_2 \rangle$")
plt.title("Magnetization over time")
[18]:
Text(0.5, 1.0, 'Magnetization over time')
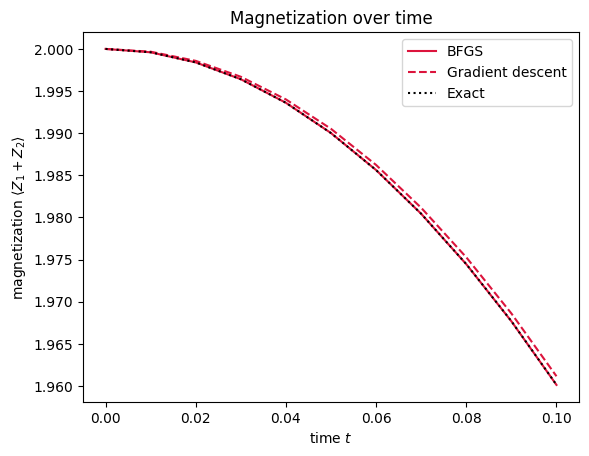
The magnetization, however, is computed very precisely.
[19]:
import tutorial_magics
%qiskit_version_table
%qiskit_copyright
Version Information
| Software | Version |
|---|---|
qiskit | 1.2.4 |
qiskit_algorithms | 0.3.1 |
| System information | |
| Python version | 3.8.18 |
| OS | Linux |
| Mon Oct 21 11:11:44 2024 UTC | |
This code is a part of a Qiskit project
© Copyright IBM 2017, 2024.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.