Note

This page was generated from docs/tutorials/07_grover_examples.ipynb.

Grover’s algorithm examples

This notebook has examples demonstrating how to use the Qiskit Algorithms Grover search algorithm, with different oracles.

We strongly recommend to run this tutorial using Qiskit 2.0 or newer. Though the use of PhaseOracle is possible in Qiskit < 2.0, it requires the tweedledum library, which has been deprecated for a long time and isn’t compatible with the most recent versions of Python.

This tutorial instead use the more recent PhaseOracleGate that has been introduced in Qiskit 2.1. Note that both are valid inputs for the oracle argument of the Grover class.

Finding solutions to 3-SAT problems

Let’s look at an example 3-Satisfiability (3-SAT) problem and walk-through how we can use Quantum Search to find its satisfying solutions. 3-SAT problems are usually expressed in Conjunctive Normal Forms (CNF) and written in the DIMACS-CNF format. For example:

input_3sat_instance = """
c example DIMACS-CNF 3-SAT
p cnf 3 5
-1 -2 -3 0
1 -2 3 0
1 2 -3 0
1 -2 -3 0
-1 2 3 0
"""

The CNF of this 3-SAT instance contains 3 variables and 5 clauses:

\((\neg v_1 \vee \neg v_2 \vee \neg v_3) \wedge (v_1 \vee \neg v_2 \vee v_3) \wedge (v_1 \vee v_2 \vee \neg v_3) \wedge (v_1 \vee \neg v_2 \vee \neg v_3) \wedge (\neg v_1 \vee v_2 \vee v_3)\)

It can be verified that this 3-SAT problem instance has three satisfying solutions:

\((v_1, v_2, v_3) = (T, F, T)\) or \((F, F, F)\) or \((T, T, F)\)

Or, expressed using the DIMACS notation:

1 -2 3, or -1 -2 -3, or 1 2 -3.

With this example problem input, we then create the corresponding oracle for our Grover search. In particular, we use the PhaseOracle component, which supports parsing DIMACS-CNF format strings and constructing the corresponding oracle circuit. Note that the PhaseOracle requires the tweedledum library if you use Qiskit in a lower version than 2.0.

from qiskit.exceptions import MissingOptionalLibraryError
from qiskit.circuit.library.phase_oracle import PhaseOracleGate
from qiskit.synthesis.boolean.boolean_expression import BooleanExpression

oracle = None
try:
    oracle = PhaseOracleGate(BooleanExpression.from_dimacs(input_3sat_instance).expression)
except ImportError as ex:
    print(ex)

The oracle can now be used to create a Grover instance:

from qiskit_algorithms import AmplificationProblem

problem = None
if oracle is not None:
    problem = AmplificationProblem(oracle)

We can then configure the backend and run the Grover instance to get the result:

from qiskit_algorithms import Grover
from qiskit.primitives import StatevectorSampler

grover = Grover(sampler=StatevectorSampler())
result = None
if problem is not None:
    result = grover.amplify(problem)
    print(result.assignment)

000

As seen above, a satisfying solution to the specified 3-SAT problem is obtained. And it is indeed one of the three satisfying solutions.

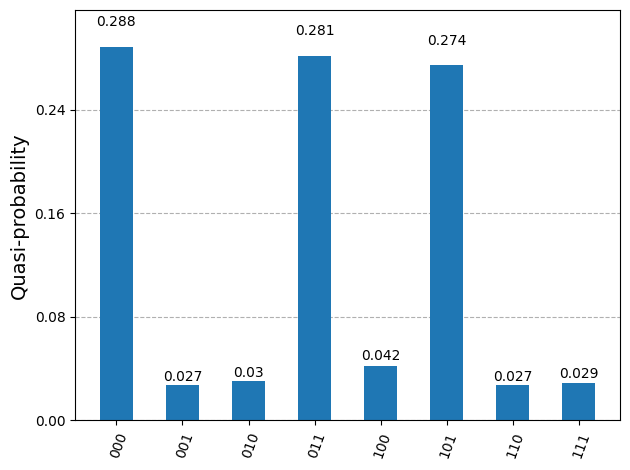
Since we used the StatevectorSampler, the complete measurement result is also returned, as shown in the plot below, where it can be seen that the binary strings 000, 011, and 101 (note the bit order in each string), corresponding to the three satisfying solutions all have high probabilities associated with them.

from qiskit.visualization import plot_histogram

if result is not None:
    display(plot_histogram(result.circuit_results[0]))

Boolean Logical Expressions

Qiskit’s Grover can also be used to perform Quantum Search on an Oracle constructed from other means, in addition to DIMACS. For example, the PhaseOracle can actually be configured using arbitrary Boolean logical expressions, as demonstrated below.

expression = "(w ^ x) & ~(y ^ z) & (x & y & z)"
try:
    oracle = PhaseOracleGate(expression)
    problem = AmplificationProblem(oracle)
    grover = Grover(sampler=StatevectorSampler())
    result = grover.amplify(problem)
    display(plot_histogram(result.circuit_results[0]))
except MissingOptionalLibraryError as ex:
    print(ex)

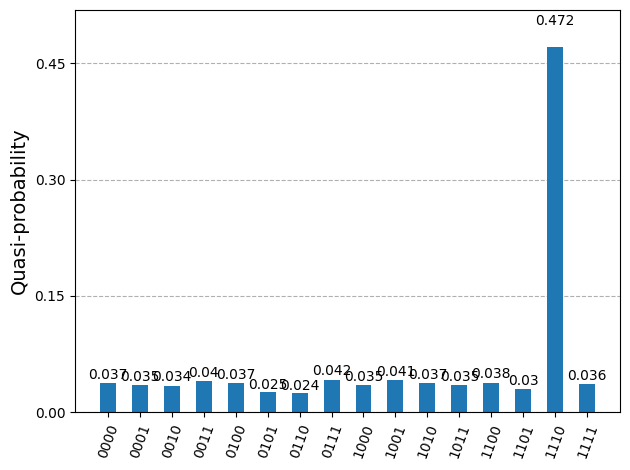
In the example above, the input Boolean logical expression '(w ^ x) & ~(y ^ z) & (x & y & z)' should be quite self-explanatory, where ^, ~, and & represent the Boolean logical XOR, NOT, and AND operators, respectively. It should be quite easy to figure out the satisfying solution by examining its parts: w ^ x calls for w and x taking different values; ~(y ^ z) requires y and z be the same; x & y & z dictates all three to be True. Putting these together, we get the satisfying solution (w, x, y, z) = (False, True, True, True), which our Grover’s result agrees with.

import tutorial_magics

%qiskit_version_table
%qiskit_copyright

Version Information

Software	Version
qiskit	2.0.3
qiskit_algorithms	0.4.0
System information
Python version	3.10.18
OS	Linux
Tue Sep 09 09:44:28 2025 UTC

This code is a part of a Qiskit project

© Copyright IBM 2017, 2025.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.