Nota

Esta página fue generada a partir de docs/tutorials/06_basket_option_pricing.ipynb.

Fijación de Precios de Opciones de Canasta#

Introducción#

Supón una opción de canasta con precio de ejercicio \(K\) y dos activos subyacentes cuyos precios al contado al vencimiento \(S_T^1\), \(S_T^2\) siguen distribuciones aleatorias dadas. La función de rendimiento correspondiente se define como:

\[\max\{S_T^1 + S_T^2 - K, 0\}\]

A continuación, se utiliza un algoritmo cuántico basado en la estimación de amplitud para estimar el rendimiento esperado, es decir, el precio justo antes del descuento, para la opción:

\[\mathbb{E}\left[ \max\{S_T^1 + S_T^2 - K, 0\} \right].\]

La aproximación de la función objetivo y una introducción general a la fijación de precios de opciones y el análisis de riesgos en computadoras cuánticas se dan en los siguientes artículos:

[1]:

import matplotlib.pyplot as plt
from scipy.interpolate import griddata

%matplotlib inline
import numpy as np

from qiskit import QuantumRegister, QuantumCircuit, AncillaRegister, transpile
from qiskit_algorithms import IterativeAmplitudeEstimation, EstimationProblem
from qiskit.circuit.library import WeightedAdder, LinearAmplitudeFunction
from qiskit_aer.primitives import Sampler
from qiskit_finance.circuit.library import LogNormalDistribution

Modelo de Incertidumbre#

Construimos un circuito para cargar una distribución aleatoria logarítmica normal multivariante en un estado cuántico en \(n\) qubits. Para cada dimensión \(j = 1,\ldots,d\), la distribución es truncada a un intervalo dado \([\text{low}_j, \text{high}_j]\) y discretizada usando una cuadrícula de \(2^{n_j}\) puntos, donde \(n_j\) denota el número de qubits usados para representar la dimensión \(j\), es decir, \(n_1+\ldots+n_d = n\). El operador unitario correspondiente al circuito implementa lo siguiente:

\[\big|0\rangle_{n} \mapsto \big|\psi\rangle_{n} = \sum_{i_1,\ldots,i_d} \sqrt{p_{i_1\ldots i_d}}\big|i_1\rangle_{n_1}\ldots\big|i_d\rangle_{n_d},\]

donde \(p_{i_1\ldots i_d}\) denota las probabilidades correspondientes a la distribución truncada y discretizada y donde \(i_j\) se asigna al intervalo correcto usando el mapa afín:

\[\{0, \ldots, 2^{n_j}-1\} \ni i_j \mapsto \frac{\text{high}_j - \text{low}_j}{2^{n_j} - 1} * i_j + \text{low}_j \in [\text{low}_j, \text{high}_j].\]

Por simplicidad, suponemos que ambos precios de las acciones son independientes y están distribuidos de manera idéntica. Esta suposición simplemente simplifica la parametrización a continuación y se puede relajar fácilmente a distribuciones multivariadas más complejas y también correlacionadas. La única suposición importante para la implementación actual es que la cuadrícula de discretización de las diferentes dimensiones tiene el mismo tamaño de paso.

[2]:

# number of qubits per dimension to represent the uncertainty
num_uncertainty_qubits = 2

# parameters for considered random distribution
S = 2.0  # initial spot price
vol = 0.4  # volatility of 40%
r = 0.05  # annual interest rate of 4%
T = 40 / 365  # 40 days to maturity

# resulting parameters for log-normal distribution
mu = (r - 0.5 * vol**2) * T + np.log(S)
sigma = vol * np.sqrt(T)
mean = np.exp(mu + sigma**2 / 2)
variance = (np.exp(sigma**2) - 1) * np.exp(2 * mu + sigma**2)
stddev = np.sqrt(variance)

# lowest and highest value considered for the spot price; in between, an equidistant discretization is considered.
low = np.maximum(0, mean - 3 * stddev)
high = mean + 3 * stddev

# map to higher dimensional distribution
# for simplicity assuming dimensions are independent and identically distributed)
dimension = 2
num_qubits = [num_uncertainty_qubits] * dimension
low = low * np.ones(dimension)
high = high * np.ones(dimension)
mu = mu * np.ones(dimension)
cov = sigma**2 * np.eye(dimension)

# construct circuit
u = LogNormalDistribution(num_qubits=num_qubits, mu=mu, sigma=cov, bounds=list(zip(low, high)))

[3]:

# plot PDF of uncertainty model
x = [v[0] for v in u.values]
y = [v[1] for v in u.values]
z = u.probabilities
# z = map(float, z)
# z = list(map(float, z))
resolution = np.array([2**n for n in num_qubits]) * 1j
grid_x, grid_y = np.mgrid[min(x) : max(x) : resolution[0], min(y) : max(y) : resolution[1]]
grid_z = griddata((x, y), z, (grid_x, grid_y))
plt.figure(figsize=(10, 8))
ax = plt.axes(projection="3d")
ax.plot_surface(grid_x, grid_y, grid_z, cmap=plt.cm.Spectral)
ax.set_xlabel("Spot Price $S_T^1$ (\$)", size=15)
ax.set_ylabel("Spot Price $S_T^2$ (\$)", size=15)
ax.set_zlabel("Probability (\%)", size=15)
plt.show()
../_images/tutorials_06_basket_option_pricing_5_0.png

Función de Rendimiento#

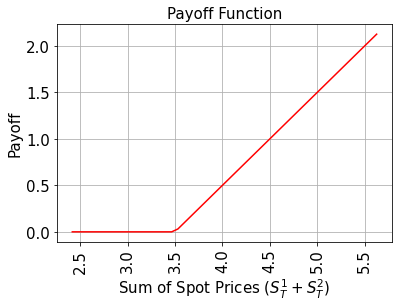
La función de rendimiento es igual a cero siempre que la suma de los precios al contado al vencimiento \((S_T^1 + S_T^2)\) sea menor que el precio de ejercicio \(K\) y luego aumenta linealmente. La implementación primero usa un operador de suma ponderada para calcular la suma de los precios al contado en un registro ancilla, y luego usa un comparador, que invierte un qubit ancilla de \(\big|0\rangle\) a \(\big|1\rangle\) si \((S_T^1 + S_T^2) \geq K\). Esta ancilla se utiliza para controlar la parte lineal de la función de rendimiento.

La parte lineal en sí se aproxima de la siguiente manera. Aprovechamos el hecho de que \(\sin^2(y + \pi/4) \approx y + 1/2\) para pequeñas \(|y|\). Por lo tanto, para un factor de cambio de escala de aproximación dado \(c_\text{approx} \in [0, 1]\) y \(x \in [0, 1]\) consideramos

\[\sin^2( \pi/2 * c_\text{approx} * ( x - 1/2 ) + \pi/4) \approx \pi/2 * c_\text{approx} * ( x - 1/2 ) + 1/2\]

para pequeños \(c_\text{approx}\).

Podemos construir fácilmente un operador que actúe como

\[\big|x\rangle \big|0\rangle \mapsto \big|x\rangle \left( \cos(a*x+b) \big|0\rangle + \sin(a*x+b) \big|1\rangle \right),\]

utilizando rotaciones Y controladas.

Finalmente, nos interesa la probabilidad de medir \(\big|1\rangle\) en el último qubit, que corresponde a \(\sin^2(a*x+b)\). Junto con la aproximación anterior, esto permite aproximar los valores de interés. Cuanto más pequeño elijamos \(c_\text{approx}\), mejor será la aproximación. Sin embargo, dado que estamos estimando una propiedad escalada por \(c_\text{approx}\), el número de qubits de evaluación \(m\) debe ajustarse en consecuencia.

Para más detalles sobre la aproximación, nos referimos a: Quantum Risk Analysis. Woerner, Egger. 2018.

Dado que el operador de suma ponderada (en su implementación actual) solo puede sumar números enteros, necesitamos mapear desde los rangos originales al rango representable para estimar el resultado y revertir este mapeo antes de interpretar el resultado. El mapeo corresponde esencialmente al mapeo afín descrito en el contexto del modelo de incertidumbre anterior.

[4]:

# determine number of qubits required to represent total loss
weights = []
for n in num_qubits:
    for i in range(n):
        weights += [2**i]

# create aggregation circuit
agg = WeightedAdder(sum(num_qubits), weights)
n_s = agg.num_sum_qubits
n_aux = agg.num_qubits - n_s - agg.num_state_qubits  # number of additional qubits

[5]:

# set the strike price (should be within the low and the high value of the uncertainty)
strike_price = 3.5

# map strike price from [low, high] to {0, ..., 2^n-1}
max_value = 2**n_s - 1
low_ = low[0]
high_ = high[0]
mapped_strike_price = (
    (strike_price - dimension * low_) / (high_ - low_) * (2**num_uncertainty_qubits - 1)
)

# set the approximation scaling for the payoff function
c_approx = 0.25

# setup piecewise linear objective fcuntion
breakpoints = [0, mapped_strike_price]
slopes = [0, 1]
offsets = [0, 0]
f_min = 0
f_max = 2 * (2**num_uncertainty_qubits - 1) - mapped_strike_price
basket_objective = LinearAmplitudeFunction(
    n_s,
    slopes,
    offsets,
    domain=(0, max_value),
    image=(f_min, f_max),
    rescaling_factor=c_approx,
    breakpoints=breakpoints,
)

[6]:

# define overall multivariate problem
qr_state = QuantumRegister(u.num_qubits, "state")  # to load the probability distribution
qr_obj = QuantumRegister(1, "obj")  # to encode the function values
ar_sum = AncillaRegister(n_s, "sum")  # number of qubits used to encode the sum
ar = AncillaRegister(max(n_aux, basket_objective.num_ancillas), "work")  # additional qubits

objective_index = u.num_qubits

basket_option = QuantumCircuit(qr_state, qr_obj, ar_sum, ar)
basket_option.append(u, qr_state)
basket_option.append(agg, qr_state[:] + ar_sum[:] + ar[:n_aux])
basket_option.append(basket_objective, ar_sum[:] + qr_obj[:] + ar[: basket_objective.num_ancillas])

print(basket_option.draw())
print("objective qubit index", objective_index)

         ┌───────┐┌────────┐
state_0: ┤0      ├┤0       ├──────
         │       ││        │
state_1: ┤1      ├┤1       ├──────
         │  P(X) ││        │
state_2: ┤2      ├┤2       ├──────
         │       ││        │
state_3: ┤3      ├┤3       ├──────
         └───────┘│        │┌────┐
    obj: ─────────┤        ├┤3   ├
                  │        ││    │
  sum_0: ─────────┤4 adder ├┤0   ├
                  │        ││    │
  sum_1: ─────────┤5       ├┤1   ├
                  │        ││    │
  sum_2: ─────────┤6       ├┤2 F ├
                  │        ││    │
 work_0: ─────────┤7       ├┤4   ├
                  │        ││    │
 work_1: ─────────┤8       ├┤5   ├
                  │        ││    │
 work_2: ─────────┤9       ├┤6   ├
                  └────────┘└────┘
objective qubit index 4

[7]:

# plot exact payoff function (evaluated on the grid of the uncertainty model)
x = np.linspace(sum(low), sum(high))
y = np.maximum(0, x - strike_price)
plt.plot(x, y, "r-")
plt.grid()
plt.title("Payoff Function", size=15)
plt.xlabel("Sum of Spot Prices ($S_T^1 + S_T^2)$", size=15)
plt.ylabel("Payoff", size=15)
plt.xticks(size=15, rotation=90)
plt.yticks(size=15)
plt.show()
../_images/tutorials_06_basket_option_pricing_10_0.png 
[8]:

# evaluate exact expected value
sum_values = np.sum(u.values, axis=1)
exact_value = np.dot(
    u.probabilities[sum_values >= strike_price],
    sum_values[sum_values >= strike_price] - strike_price,
)
print("exact expected value:\t%.4f" % exact_value)

exact expected value:   0.4870

Evaluar el Rendimiento Esperado#

Primero verificamos el circuito cuántico simulándolo y analizando la probabilidad resultante para medir el estado \(|1\rangle\) en el qubit objetivo.

[9]:

num_state_qubits = basket_option.num_qubits - basket_option.num_ancillas
print("state qubits: ", num_state_qubits)
transpiled = transpile(basket_option, basis_gates=["u", "cx"])
print("circuit width:", transpiled.width())
print("circuit depth:", transpiled.depth())

state qubits:  5
circuit width: 11
circuit depth: 415

[10]:

basket_option_measure = basket_option.measure_all(inplace=False)
sampler = Sampler()
job = sampler.run(basket_option_measure)

[11]:

# evaluate the result
value = 0
probabilities = job.result().quasi_dists[0].binary_probabilities()
for i, prob in probabilities.items():
    if prob > 1e-4 and i[-num_state_qubits:][0] == "1":
        value += prob


# map value to original range
mapped_value = (
    basket_objective.post_processing(value) / (2**num_uncertainty_qubits - 1) * (high_ - low_)
)
print("Exact Operator Value:  %.4f" % value)
print("Mapped Operator value: %.4f" % mapped_value)
print("Exact Expected Payoff: %.4f" % exact_value)

Exact Operator Value:  0.4209
Mapped Operator value: 0.6350
Exact Expected Payoff: 0.4870

A continuación, usamos la estimación de amplitud para estimar el rendimiento esperado.

[12]:

# set target precision and confidence level
epsilon = 0.01
alpha = 0.05

problem = EstimationProblem(
    state_preparation=basket_option,
    objective_qubits=[objective_index],
    post_processing=basket_objective.post_processing,
)
# construct amplitude estimation
ae = IterativeAmplitudeEstimation(
    epsilon_target=epsilon, alpha=alpha, sampler=Sampler(run_options={"shots": 100, "seed": 75})
)

[13]:

result = ae.estimate(problem)

[14]:

conf_int = (
    np.array(result.confidence_interval_processed)
    / (2**num_uncertainty_qubits - 1)
    * (high_ - low_)
)
print("Exact value:        \t%.4f" % exact_value)
print(
    "Estimated value:    \t%.4f"
    % (result.estimation_processed / (2**num_uncertainty_qubits - 1) * (high_ - low_))
)
print("Confidence interval:\t[%.4f, %.4f]" % tuple(conf_int))

Exact value:            0.4870
Estimated value:        0.4945
Confidence interval:    [0.4821, 0.5069]

[15]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

SoftwareVersion
qiskitNone
qiskit-terra0.45.0.dev0+c626be7
qiskit_finance0.4.0
qiskit_ibm_provider0.6.1
qiskit_aer0.12.0
qiskit_algorithms0.2.0
System information
Python version3.9.7
Python compilerGCC 7.5.0
Python builddefault, Sep 16 2021 13:09:58
OSLinux
CPUs2
Memory (Gb)5.778430938720703
Fri Aug 18 16:17:28 2023 EDT

This code is a part of Qiskit

© Copyright IBM 2017, 2023.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.

[ ]: