Nota
Esta página fue generada a partir de docs/tutorials/00_amplitude_estimation.ipynb.
Estimación de Amplitud Cuántica#
Dado un operador \(\mathcal{A}\) que actúa como
La Estimación de Amplitud Cuántica (Quantum Amplitude Estimation, QAE) es la tarea de encontrar una estimación de la amplitud \(a\) del estado \(|\Psi_1\rangle\):
Esta tarea fue investigada por primera vez por Brassard et al. [1] en 2000 y su algoritmo utiliza una combinación del operador Grover
donde \(\mathcal{S}_0\) y \(\mathcal{S}_{\Psi_1}\) son reflexiones sobre los estados \(|0\rangle\) y \(|\Psi_1\rangle\), respectivamente, y la estimación de fase. Sin embargo, este algoritmo, llamado AmplitudeEstimation en Qiskit Algorithms, requiere circuitos grandes y es computacionalmente costoso. Por lo tanto, se han propuesto otras variantes de QAE, que mostraremos en este tutorial para un ejemplo simple.
En nuestro ejemplo, \(\mathcal{A}\) describe una variable aleatoria de Bernoulli con (supongamos desconocida) probabilidad de éxito \(p\):
En una computadora cuántica, podemos modelar este operador con una rotación alrededor del eje \(Y\) de un solo qubit
El operador Grover para este caso es particularmente simple
cuyas potencias son muy fáciles de calcular: \(\mathcal{Q}^k = R_Y(2k\theta_p)\).
Fijaremos la probabilidad que queremos estimar en \(p = 0.2\).
[1]:
p = 0.2
Ahora podemos definir circuitos para \(\mathcal{A}\) y \(\mathcal{Q}\).
[2]:
import numpy as np
from qiskit.circuit import QuantumCircuit
class BernoulliA(QuantumCircuit):
"""A circuit representing the Bernoulli A operator."""
def __init__(self, probability):
super().__init__(1) # circuit on 1 qubit
theta_p = 2 * np.arcsin(np.sqrt(probability))
self.ry(theta_p, 0)
class BernoulliQ(QuantumCircuit):
"""A circuit representing the Bernoulli Q operator."""
def __init__(self, probability):
super().__init__(1) # circuit on 1 qubit
self._theta_p = 2 * np.arcsin(np.sqrt(probability))
self.ry(2 * self._theta_p, 0)
def power(self, k):
# implement the efficient power of Q
q_k = QuantumCircuit(1)
q_k.ry(2 * k * self._theta_p, 0)
return q_k
[3]:
A = BernoulliA(p)
Q = BernoulliQ(p)
Flujo de Trabajo de Estimación de Amplitud#
Qiskit Algorithms implementa varios algoritmos QAE que se derivan de la interfaz AmplitudeEstimator. En el inicializador especificamos la configuración específica del algoritmo y el método de estimate que hace todo el trabajo, toma un EstimationProblem como entrada y devuelve un objeto AmplitudeEstimationResult. Dado que todas las variantes de QAE siguen la misma interfaz, podemos usarlas todas para resolver la misma instancia de problema.
A continuación, ejecutaremos todos los diferentes algoritmos de QAE. Para hacerlo, primero definimos el problema de estimación que contendrá los operadores \(\mathcal{A}\) y \(\mathcal{Q}\) así como también cómo identificar el estado \(|\Psi_1\rangle\), que en este ejemplo simple es \(|1\rangle\).
[4]:
from qiskit_algorithms import EstimationProblem
problem = EstimationProblem(
state_preparation=A, # A operator
grover_operator=Q, # Q operator
objective_qubits=[0], # the "good" state Psi1 is identified as measuring |1> in qubit 0
)
Para ejecutar circuitos usaremos Sampler.
[5]:
from qiskit.primitives import Sampler
sampler = Sampler()
AE Canónica#
Ahora solucionemos esto con la implementación QAE original de Brassard et al. [1].
[6]:
from qiskit_algorithms import AmplitudeEstimation
ae = AmplitudeEstimation(
num_eval_qubits=3, # the number of evaluation qubits specifies circuit width and accuracy
sampler=sampler,
)
Con el algoritmo definido, podemos llamar al método estimate y proporcionarle el problema a resolver.
[7]:
ae_result = ae.estimate(problem)
La estimación está disponible en la llave de estimation:
[8]:
print(ae_result.estimation)
0.1464466
¡Vemos que esta no es una estimación muy buena para nuestro objetivo de \(p=0.2\)! Eso se debe al hecho de que la AE canónica está restringida a una cuadrícula discreta, especificada por el número de qubits de evaluación:
[9]:
import matplotlib.pyplot as plt
# plot estimated values
gridpoints = list(ae_result.samples.keys())
probabilities = list(ae_result.samples.values())
plt.bar(gridpoints, probabilities, width=0.5 / len(probabilities))
plt.axvline(p, color="r", ls="--")
plt.xticks(size=15)
plt.yticks([0, 0.25, 0.5, 0.75, 1], size=15)
plt.title("Estimated Values", size=15)
plt.ylabel("Probability", size=15)
plt.xlabel(r"Amplitude $a$", size=15)
plt.ylim((0, 1))
plt.grid()
plt.show()
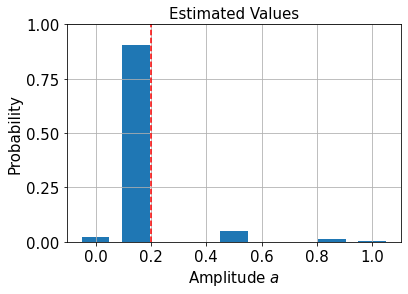
Para mejorar la estimación, podemos interpolar las probabilidades de medición y calcular el estimador de máxima verosimilitud que produce esta distribución de probabilidad:
[10]:
print("Interpolated MLE estimator:", ae_result.mle)
Interpolated MLE estimator: 0.19999999406856905
Podemos echar un vistazo al circuito que AE ejecuta:
[11]:
ae_circuit = ae.construct_circuit(problem)
ae_circuit.decompose().draw(
"mpl", style="iqx"
) # decompose 1 level: exposes the Phase estimation circuit!
[11]:
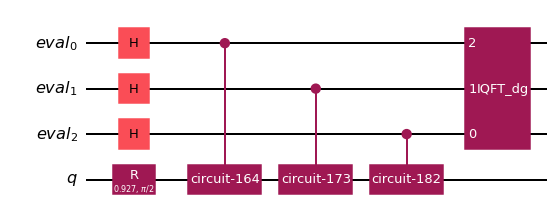
[12]:
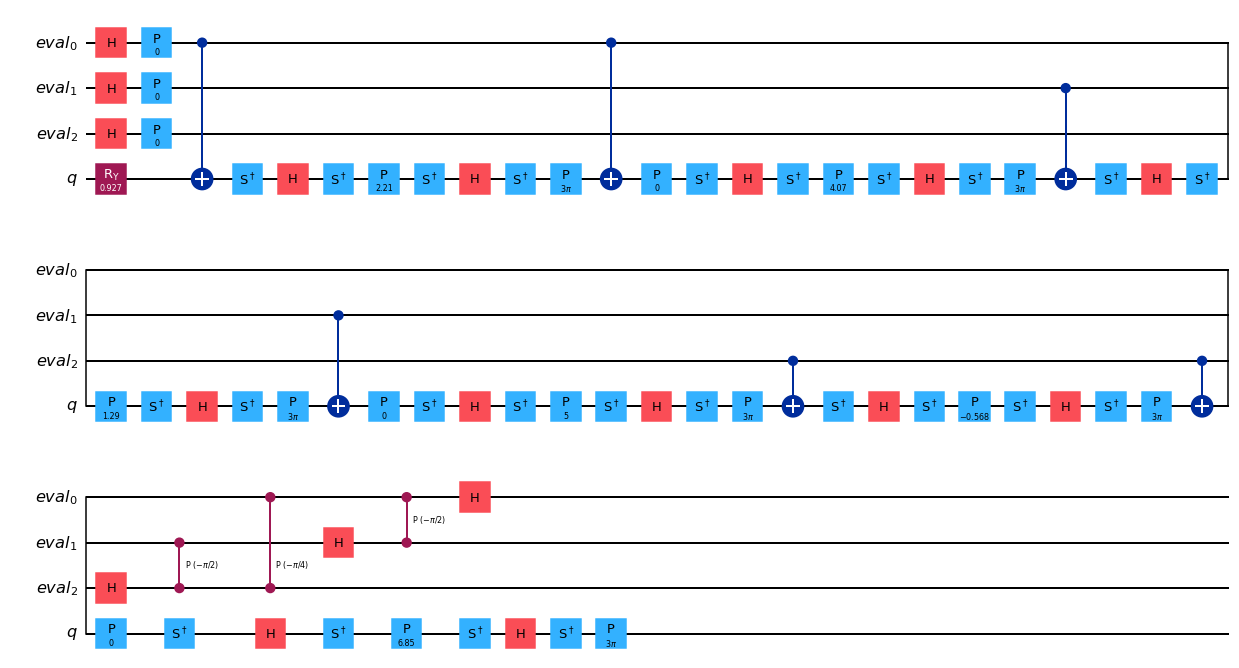
from qiskit import transpile
basis_gates = ["h", "ry", "cry", "cx", "ccx", "p", "cp", "x", "s", "sdg", "y", "t", "cz"]
transpile(ae_circuit, basis_gates=basis_gates, optimization_level=2).draw("mpl", style="iqx")
[12]:
Estimación de Amplitud Iterativa#
Véase [2].
[13]:
from qiskit_algorithms import IterativeAmplitudeEstimation
iae = IterativeAmplitudeEstimation(
epsilon_target=0.01, # target accuracy
alpha=0.05, # width of the confidence interval
sampler=sampler,
)
iae_result = iae.estimate(problem)
print("Estimate:", iae_result.estimation)
Estimate: 0.2
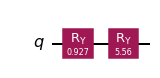
¡Los circuitos de aquí solo consisten en potencias de Grover y son mucho más baratos!
[14]:
iae_circuit = iae.construct_circuit(problem, k=3)
iae_circuit.draw("mpl", style="iqx")
[14]:
Estimación de Amplitud de Máxima Verosimilitud#
Véase [3].
[15]:
from qiskit_algorithms import MaximumLikelihoodAmplitudeEstimation
mlae = MaximumLikelihoodAmplitudeEstimation(
evaluation_schedule=3, # log2 of the maximal Grover power
sampler=sampler,
)
mlae_result = mlae.estimate(problem)
print("Estimate:", mlae_result.estimation)
Estimate: 0.20002237175368104
Estimación de Amplitud Más Rápida#
Véase [4].
[18]:
from qiskit_algorithms import FasterAmplitudeEstimation
fae = FasterAmplitudeEstimation(
delta=0.01, # target accuracy
maxiter=3, # determines the maximal power of the Grover operator
sampler=sampler,
)
fae_result = fae.estimate(problem)
print("Estimate:", fae_result.estimation)
Estimate: 0.2030235918323876
Referencias#
[1] Quantum Amplitude Amplification and Estimation. Brassard et al (2000). https://arxiv.org/abs/quant-ph/0005055
[2] Iterative Quantum Amplitude Estimation. Grinko, D., Gacon, J., Zoufal, C., & Woerner, S. (2019). https://arxiv.org/abs/1912.05559
[3] Amplitude Estimation without Phase Estimation. Suzuki, Y., Uno, S., Raymond, R., Tanaka, T., Onodera, T., & Yamamoto, N. (2019). https://arxiv.org/abs/1904.10246
[4] Faster Amplitude Estimation. K. Nakaji (2020). https://arxiv.org/pdf/2003.02417.pdf
[17]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Software | Version |
|---|---|
qiskit | None |
qiskit-terra | 0.45.0.dev0+c626be7 |
qiskit_ibm_provider | 0.6.1 |
qiskit_algorithms | 0.2.0 |
| System information | |
| Python version | 3.9.7 |
| Python compiler | GCC 7.5.0 |
| Python build | default, Sep 16 2021 13:09:58 |
| OS | Linux |
| CPUs | 2 |
| Memory (Gb) | 5.778430938720703 |
| Fri Aug 18 15:44:17 2023 EDT | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: