Nota

Esta página fue generada a partir de docs/tutorials/04_european_put_option_pricing.ipynb.

Fijación de Precios de Opciones de Venta Europeas

Introducción

Supón una opción de venta europea con precio de ejercicio \(K\) y un activo subyacente cuyo precio de contado al vencimiento \(S_T\) sigue una distribución aleatoria dada. La función de pago correspondiente se define como:

\[\max\{K - S_T, 0\}\]

A continuación, se utiliza un algoritmo cuántico basado en la estimación de amplitud para estimar el rendimiento esperado, es decir, el precio justo antes del descuento, para la opción:

\[\mathbb{E}\left[ \max\{K - S_T, 0\} \right]\]

así como la correspondiente \(\Delta\), es decir, el derivado del precio de la opción con respecto al precio al contado, definido como:

\[\Delta = -\mathbb{P}\left[S_T \leq K\right]\]

La aproximación de la función objetivo y una introducción general a la fijación de precios de opciones y el análisis de riesgos en computadoras cuánticas se dan en los siguientes artículos:

• Quantum Risk Analysis. Woerner, Egger. 2018.

• Option Pricing using Quantum Computers. Stamatopoulos et al. 2019.

import matplotlib.pyplot as plt

%matplotlib inline
import numpy as np

from qiskit_algorithms import IterativeAmplitudeEstimation, EstimationProblem
from qiskit.circuit.library import LinearAmplitudeFunction
from qiskit_aer.primitives import Sampler
from qiskit_finance.circuit.library import LogNormalDistribution

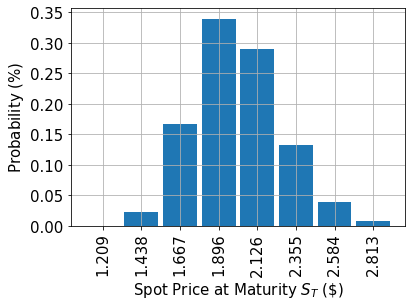
Modelo de Incertidumbre

Construimos un circuito para cargar una distribución aleatoria logarítmica normal en un estado cuántico. La distribución se trunca a un intervalo dado \([\text{low}, \text{high}]\) y discretiza usando una cuadrícula con \(2^n\) puntos, donde \(n\) denota el número de qubits utilizados. El operador unitario correspondiente al circuito implementa lo siguiente:

\[\big|0\rangle_{n} \mapsto \big|\psi\rangle_{n} = \sum_{i=0}^{2^n-1} \sqrt{p_i}\big|i\rangle_{n},\]

donde \(p_i\) denota las probabilidades correspondientes a la distribución truncada y discretizada y donde \(i\) se asigna al intervalo correcto usando el mapa afín:

\[\{0, \ldots, 2^n-1\} \ni i \mapsto \frac{\text{high} - \text{low}}{2^n - 1} * i + \text{low} \in [\text{low}, \text{high}].\]

# number of qubits to represent the uncertainty
num_uncertainty_qubits = 3

# parameters for considered random distribution
S = 2.0  # initial spot price
vol = 0.4  # volatility of 40%
r = 0.05  # annual interest rate of 4%
T = 40 / 365  # 40 days to maturity

# resulting parameters for log-normal distribution
mu = (r - 0.5 * vol**2) * T + np.log(S)
sigma = vol * np.sqrt(T)
mean = np.exp(mu + sigma**2 / 2)
variance = (np.exp(sigma**2) - 1) * np.exp(2 * mu + sigma**2)
stddev = np.sqrt(variance)

# lowest and highest value considered for the spot price; in between, an equidistant discretization is considered.
low = np.maximum(0, mean - 3 * stddev)
high = mean + 3 * stddev

# construct A operator for QAE for the payoff function by
# composing the uncertainty model and the objective
uncertainty_model = LogNormalDistribution(
    num_uncertainty_qubits, mu=mu, sigma=sigma**2, bounds=(low, high)
)

# plot probability distribution
x = uncertainty_model.values
y = uncertainty_model.probabilities
plt.bar(x, y, width=0.2)
plt.xticks(x, size=15, rotation=90)
plt.yticks(size=15)
plt.grid()
plt.xlabel("Spot Price at Maturity $S_T$ (\$)", size=15)
plt.ylabel("Probability ($\%$)", size=15)
plt.show()

Función de Rendimiento

La función de rendimiento disminuye linealmente con un precio de contado creciente al vencimiento \(S_T\) hasta que llega a cero para un precio de contado igual al precio de ejercicio \(K\), permanece constante a cero para precios de contado más altos. La implementación usa un comparador, que cambia un qubit ancilla de \(\big|0\rangle\) a \(\big|1\rangle\) si \(S_T \leq K\), y esta ancilla es se utiliza para controlar la parte lineal de la función de pago.

La parte lineal en sí se aproxima entonces de la siguiente manera. Aprovechamos el hecho de que \(\sin^2(y + \pi/4) \approx y + 1/2\) para pequeños valores de \(|y|\). Por lo tanto, para un factor de escalamiento de aproximación dado \(c_\text{approx} \in [0, 1]\) y \(x \in [0, 1]\) consideramos

\[\sin^2( \pi/2 * c_\text{approx} * ( x - 1/2 ) + \pi/4) \approx \pi/2 * c_\text{approx} * ( x - 1/2 ) + 1/2\]

para pequeños \(c_\text{approx}\).

Podemos construir fácilmente un operador que actúe como

\[\big|x\rangle \big|0\rangle \mapsto \big|x\rangle \left( \cos(a*x+b) \big|0\rangle + \sin(a*x+b) \big|1\rangle \right),\]

utilizando rotaciones Y controladas.

Finalmente, nos interesa la probabilidad de medir \(\big|1\rangle\) en el último qubit, que corresponde a \(\sin^2(a*x+b)\). Junto con la aproximación anterior, esto permite aproximar los valores de interés. Cuanto más pequeño elijamos \(c_\text{approx}\), mejor será la aproximación. Sin embargo, dado que estamos estimando una propiedad escalada por \(c_\text{approx}\), el número de qubits de evaluación \(m\) debe ajustarse en consecuencia.

Para más detalles sobre la aproximación, nos referimos a: Quantum Risk Analysis. Woerner, Egger. 2018.

# set the strike price (should be within the low and the high value of the uncertainty)
strike_price = 2.126

# set the approximation scaling for the payoff function
rescaling_factor = 0.25

# setup piecewise linear objective fcuntion
breakpoints = [low, strike_price]
slopes = [-1, 0]
offsets = [strike_price - low, 0]
f_min = 0
f_max = strike_price - low
european_put_objective = LinearAmplitudeFunction(
    num_uncertainty_qubits,
    slopes,
    offsets,
    domain=(low, high),
    image=(f_min, f_max),
    breakpoints=breakpoints,
    rescaling_factor=rescaling_factor,
)

# construct A operator for QAE for the payoff function by
# composing the uncertainty model and the objective
european_put = european_put_objective.compose(uncertainty_model, front=True)

# plot exact payoff function (evaluated on the grid of the uncertainty model)
x = uncertainty_model.values
y = np.maximum(0, strike_price - x)
plt.plot(x, y, "ro-")
plt.grid()
plt.title("Payoff Function", size=15)
plt.xlabel("Spot Price", size=15)
plt.ylabel("Payoff", size=15)
plt.xticks(x, size=15, rotation=90)
plt.yticks(size=15)
plt.show()

# evaluate exact expected value (normalized to the [0, 1] interval)
exact_value = np.dot(uncertainty_model.probabilities, y)
exact_delta = -sum(uncertainty_model.probabilities[x <= strike_price])
print("exact expected value:\t%.4f" % exact_value)
print("exact delta value:   \t%.4f" % exact_delta)

exact expected value:   0.1709
exact delta value:      -0.8193

Evaluar el Rendimiento Esperado

# set target precision and confidence level
epsilon = 0.01
alpha = 0.05

problem = EstimationProblem(
    state_preparation=european_put,
    objective_qubits=[num_uncertainty_qubits],
    post_processing=european_put_objective.post_processing,
)
# construct amplitude estimation
ae = IterativeAmplitudeEstimation(
    epsilon_target=epsilon, alpha=alpha, sampler=Sampler(run_options={"shots": 100, "seed": 75})
)

result = ae.estimate(problem)

conf_int = np.array(result.confidence_interval_processed)
print("Exact value:        \t%.4f" % exact_value)
print("Estimated value:    \t%.4f" % (result.estimation_processed))
print("Confidence interval:\t[%.4f, %.4f]" % tuple(conf_int))

Exact value:            0.1709
Estimated value:        0.1770
Confidence interval:    [0.1720, 0.1820]

Evaluar Delta

La Delta es un poco más simple de evaluar que el rendimiento esperado. De manera similar al rendimiento esperado, usamos un circuito comparador y un qubit ancilla para identificar los casos donde \(S_T \leq K\). Sin embargo, dado que solo nos interesa la probabilidad (negativa) de que esta condición sea cierta, podemos usar directamente este qubit ancilla como el qubit objetivo en la estimación de amplitud sin ninguna aproximación adicional.

# setup piecewise linear objective fcuntion
breakpoints = [low, strike_price]
slopes = [0, 0]
offsets = [1, 0]
f_min = 0
f_max = 1

european_put_delta_objective = LinearAmplitudeFunction(
    num_uncertainty_qubits,
    slopes,
    offsets,
    domain=(low, high),
    image=(f_min, f_max),
    breakpoints=breakpoints,
)

# construct circuit for payoff function
european_put_delta = european_put_delta_objective.compose(uncertainty_model, front=True)

# set target precision and confidence level
epsilon = 0.01
alpha = 0.05

problem = EstimationProblem(
    state_preparation=european_put_delta, objective_qubits=[num_uncertainty_qubits]
)
# construct amplitude estimation
ae_delta = IterativeAmplitudeEstimation(
    epsilon_target=epsilon, alpha=alpha, sampler=Sampler(run_options={"shots": 100, "seed": 75})
)

result_delta = ae_delta.estimate(problem)

conf_int = -np.array(result_delta.confidence_interval)[::-1]
print("Exact delta:    \t%.4f" % exact_delta)
print("Estimated value: \t%.4f" % -result_delta.estimation)
print("Confidence interval: \t[%.4f, %.4f]" % tuple(conf_int))

Exact delta:            -0.8193
Estimated value:        -0.8197
Confidence interval:    [-0.8236, -0.8158]

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Software	Version
qiskit	None
qiskit-terra	0.45.0.dev0+c626be7
qiskit_aer	0.12.0
qiskit_algorithms	0.2.0
qiskit_finance	0.4.0
qiskit_ibm_provider	0.6.1
System information
Python version	3.9.7
Python compiler	GCC 7.5.0
Python build	default, Sep 16 2021 13:09:58
OS	Linux
CPUs	2
Memory (Gb)	5.778430938720703
Fri Aug 18 16:14:14 2023 EDT

This code is a part of Qiskit

© Copyright IBM 2017, 2023.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.