Qiskit Machine Learning v0.5 Migration Guide#
This tutorial will guide you through the process of migrating your code from Qiskit Machine Learning v0.4 to v0.5.
Introduction#
The main focus of the 0.5 release of Qiskit Machine Learning is the migration of the base computational blocks like quantum kernels and quantum neural networks to the primitives introduced in Qiskit as well as extended support of the primitives in the algorithms.
Contents:
Overview of the primitives
New quantum kernel
New quantum neural networks
Other notable deprecation
Overview of the primitives#
The core capability of quantum computers that sets them apart from from classical computers is their ability to generate non-classical probability distributions at their outputs. The native operations that one can do with a probability distribution is to sample from it or to estimate quantities on it. Consequently, these operations of sampling and estimating form the fundamental building blocks of quantum algorithm development. Thus, as it was announced, two basic primitives were introduced, Sampler and Estimator, respectively, that implement these two operations:
Sampler class calculates probabilities or quasi-probabilities of bitstrings from quantum circuits. The base class is qiskit.primitives.BaseSampler.
Estimator class estimates expectation values of quantum circuits and observables. The base class is qiskit.primitives.BaseEstimator.
Qiskit Terra provides core interfaces and two implementations:
The reference implementation that is statevector based. This implementation does require a backend or a simulator, it relies on the classes from the quantum_info package.
The backend based primitives are to support provider/backends that do not support primitives directly. This implementation requires an instance of a backend to be passed to a primitive.
More information on the Qiskit Terra primitives can be found in the documentation.
It is worth mentioning other implementations as well:
Aer primitives should be used for Aer simulator. They extend corresponding interfaces from Terra and can be used in the same way as primitives from Terra. See documentation for more information.
The runtime primitives to be used with IBM devices. This is an implementation that is focused on cloud computing on actual hardware. See here.
Along with the primitives Terra has some primitive-like algorithms that are highly useful in QML and used by the new 0.5 functions:
Algorithms to calculate the gradient of a quantum circuit. For each core primitive there’s a corresponding base interface that defines quantum circuit gradient. The documentation on gradients is here.
Algorithms that compute the fidelity or “closeness” of pairs of quantum states. Currently, only one implementation is available that requires a sampler primitive and is based on the compute-uncompute method. The documentation is here.
Both two new algorithms are very similar to the core primitives, they share the same method signatures, so they may be called as high level primitives despite they are not in the primitives package.
New quantum kernel#
The previous implementation consisted of a single class QuantumKernel that did everything:
Constructed circuits
Executed circuits and evaluated overlap between circuits
Provided training parameters
Kept track of the values assigned to the parameters.
The implementation became sophisticated and inflexible and adding support of the new primitives could be tricky. To address the issues, a new flexible and extendable design of quantum kernels was introduced. The goals of the new design are:
Migrate to the primitives and leverage the fidelity algorithm. Now users may plug in their own implementations of fidelity calculations.
Extract trainability feature to a dedicated class.
Introduce a base class that can be extended by other kernel implementations.
The new design of quantum kernel is shown on the next diagram.
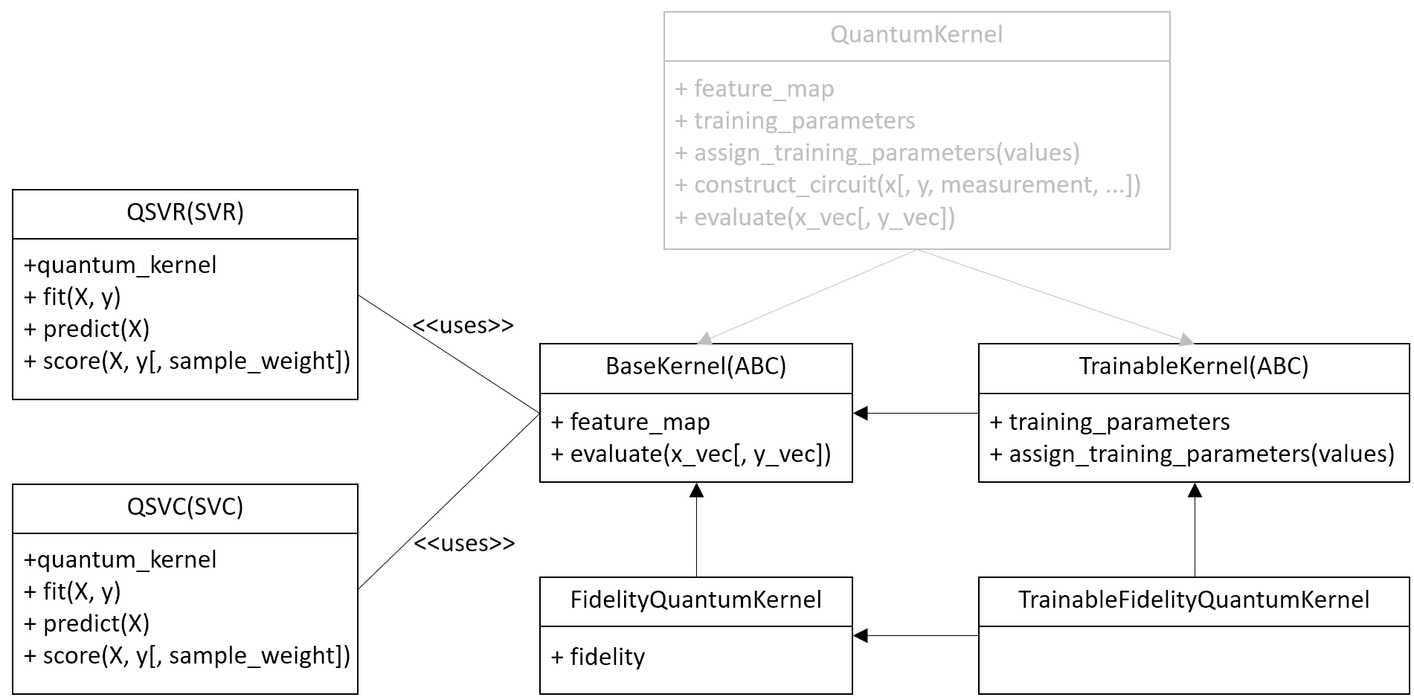
The new kernels expose the same interface and the same parameters except
the quantum_instance parameter. This parameter does not have a
direct replacement and instead the fidelity parameter must be used.
The backend handling/selection, which was previously done using the
quantum_instance, is now taken care of via the Sampler primitive
given to the fidelity.
A new hierarchy shown on the diagram introduces:
A base and abstract class BaseKernel is introduced. All concrete implementation must inherit this class.
A fidelity based quantum kernel FidelityQuantumKernel is added. This is a direct replacement of the previous quantum kernel implementation. The difference is that the new class takes a fidelity instance to estimate overlaps and construct kernel matrix.
A new abstract class TrainableKernel is introduced to generalize ability to train quantum kernels.
A fidelity-based trainable quantum kernel TrainableFidelityQuantumKernel is introduced. This is a replacement of the previous quantum kernel if a trainable kernel is required. The trainer QuantumKernelTrainer now accepts both quantum kernel implementations, the new one and the previous one.
For convenience, the previous quantum kernel implementation, QuantumKernel, now extends both new abstract classes and thus it is compatible with the new introduced interfaces. This implementation is now pending deprecation, will be deprecated in a future release and subsequently removed after that. New, primitive-based quantum kernels should be used instead.
The existing algorithms such as QSVC, QSVR and other kernel-based algorithms are updated and work with both implementations.
For example a QSVM classifier can be trained as follows.
Create a dataset#
Fixing randomization.
from qiskit.utils import algorithm_globals
algorithm_globals.random_seed = 123456
Generate a simple dataset using scikit-learn.
from sklearn.datasets import make_blobs
features, labels = make_blobs(
n_samples=20,
centers=2,
center_box=(-1, 1),
cluster_std=0.1,
random_state=algorithm_globals.random_seed,
)
Previous implementation of quantum kernel#
In the previous implementation we start from creating an instance of
QuantumInstance. This class defines where our quantum circuits are
executed. In this case we wrap a statevector simulator in the quantum
instance.
from qiskit import BasicAer
from qiskit.utils import QuantumInstance
sv_qi = QuantumInstance(
BasicAer.get_backend("statevector_simulator"),
seed_simulator=algorithm_globals.random_seed,
seed_transpiler=algorithm_globals.random_seed,
)
Then create a quantum kernel.
from qiskit.circuit.library import ZZFeatureMap
from qiskit_machine_learning.kernels import QuantumKernel
feature_map = ZZFeatureMap(2)
previous_kernel = QuantumKernel(feature_map=feature_map, quantum_instance=sv_qi)
And finally we fit an SVM classifier.
from qiskit_machine_learning.algorithms import QSVC
qsvc = QSVC(quantum_kernel=previous_kernel)
qsvc.fit(features, labels)
qsvc.score(features, labels)
0.95
New implementation of quantum kernel#
In the new implementation we start from creating a Fidelity instance. Fidelity is optional and quantum kernel will create it automatically if none is passed. But here, we create it manually for illustrative purposes. To create a fidelity instance we pass a sampler. The sampler is the reference implementation and defines where our quantum circuits are executed. You may create a sampler instance from QiskitRuntimeService to leverage Qiskit runtime services.
from qiskit.algorithms.state_fidelities import ComputeUncompute
from qiskit.primitives import Sampler
fidelity = ComputeUncompute(sampler=Sampler())
Next, we create a new quantum kernel with the fidelity instance.
from qiskit_machine_learning.kernels import FidelityQuantumKernel
feature_map = ZZFeatureMap(2)
new_kernel = FidelityQuantumKernel(feature_map=feature_map, fidelity=fidelity)
Then we fit an SVM classifier the same way as before.
from qiskit_machine_learning.algorithms import QSVC
qsvc = QSVC(quantum_kernel=new_kernel)
qsvc.fit(features, labels)
qsvc.score(features, labels)
0.95
New quantum neural networks#
Changes in the quantum neural networks are not as dramatic as in quantum kernels. In addition, and as a replacement to the existing neural networks, two new networks are introduced. The new networks introduced are SamplerQNN and EstimatorQNN which are detailed below and are replacements for the pre-existing CircuitQNN, OpflowQNN and TwoLayerQNN which are now pending deprecated.
SamplerQNN#
A new Sampler Quantum Neural Network leverages the sampler primitive, sampler gradients and is a direct replacement of CircuitQNN.
The new
SamplerQNN
exposes a similar interface to the existing
CircuitQNN,
with a few differences. One is the quantum_instance parameter. This
parameter does not have a direct replacement, and instead the
sampler parameter must be used. The gradient parameter keeps the
same name as in the
CircuitQNN
implementation, but it no longer accepts Opflow gradient classes as
inputs; instead, this parameter expects an (optionally custom) primitive
gradient. The sampling option has been removed for the time being,
as this information is not currently exposed by the sampler, and might
correspond to future lower-level primitives.
The existing training algorithms such as VQC that were based on CircuitQNN, are updated to accept both implementations. The implementation of NeuralNetworkClassifier has not changed.
The existing CircuitQNN is now pending deprecation, will be deprecated in a future release and subsequently removed after that.
We’ll show how to train a variational quantum classifier using both networks. For this purposes we re-use the dataset generated for the quantum kernel. For both quantum neural networks we still have to construct a feature map, an ansatz and combine them into a single quantum circuit.
from qiskit import QuantumCircuit
from qiskit.circuit.library import RealAmplitudes
num_inputs = 2
feature_map = ZZFeatureMap(num_inputs)
ansatz = RealAmplitudes(num_inputs, reps=1)
circuit = QuantumCircuit(num_inputs)
circuit.compose(feature_map, inplace=True)
circuit.compose(ansatz, inplace=True)
We need an interpret function as well. We define our usual parity function that maps bitstrings either to \(0\) or \(1\).
def parity(x):
return "{:b}".format(x).count("1") % 2
We fix the initial point to get the same results from both networks.
initial_point = algorithm_globals.random.random(ansatz.num_parameters)
Building a classifier using CircuitQNN#
We create a CircuitQNN instance and re-use the quantum instance
created for the quantum kernel.
from qiskit_machine_learning.neural_networks import CircuitQNN
circuit_qnn = CircuitQNN(
circuit=circuit,
input_params=feature_map.parameters,
weight_params=ansatz.parameters,
interpret=parity,
output_shape=2,
quantum_instance=sv_qi,
)
Construct a classifier out of the network, train it and score it. We are not aiming for good results, so the number of iterations is set to a small number to reduce overall execution time.
from qiskit.algorithms.optimizers import COBYLA
from qiskit_machine_learning.algorithms import NeuralNetworkClassifier
classifier = NeuralNetworkClassifier(
neural_network=circuit_qnn,
loss="cross_entropy",
one_hot=True,
optimizer=COBYLA(maxiter=40),
initial_point=initial_point,
)
classifier.fit(features, labels)
classifier.score(features, labels)
0.6
Building a classifier using SamplerQNN#
Instead of QuantumInstance create an instance of the reference
Sampler.
from qiskit.primitives import Sampler
sampler = Sampler()
Now, we create a instance of SamplerQNN. The difference with
CircuitQNN is that we pass a sampler instead of a quantum instance.
from qiskit_machine_learning.neural_networks import SamplerQNN
sampler_qnn = SamplerQNN(
circuit=circuit,
input_params=feature_map.parameters,
weight_params=ansatz.parameters,
interpret=parity,
output_shape=2,
sampler=sampler,
)
Construct a classifier and fit it as usual. As neural_network we
pass a created SamplerQNN and this is the only difference.
classifier = NeuralNetworkClassifier(
neural_network=sampler_qnn,
loss="cross_entropy",
one_hot=True,
optimizer=COBYLA(maxiter=40),
initial_point=initial_point,
)
classifier.fit(features, labels)
classifier.score(features, labels)
0.6
Instead of constructing a quantum neural network manually, you may train
VQC. It takes either a quantum instance or a sampler, depending on
what is passed it automatically constructs either CircuitQNN or
SamplerQNN respectively.
EstimatorQNN#
A new Estimator quantum neural network leverages the estimator primitive, estimator gradients and is a direct replacement of OpflowQNN.
The new
EstimatorQNN
exposes a similar interface to the existing
OpflowQNN,
with a few differences. One is the quantum_instance parameter. This
parameter does not have a direct replacement, and instead the
estimator parameter must be used. The gradient parameter keeps
the same name as in the
OpflowQNN
implementation, but it no longer accepts Opflow gradient classes as
inputs; instead, this parameter expects an (optionally custom) primitive
gradient.
The existing training algorithms such as VQR that were based on the TwoLayerQNN, are updated to accept both implementations. The implementation of NeuralNetworkRegressor has not changed.
The existing OpflowQNN is now pending deprecation, will be deprecated in a future release and subsequently removed after that.
We’ll show how to train a variational quantum regressor using both networks. We start from generating a simple regression dataset.
import numpy as np
num_samples = 20
eps = 0.2
lb, ub = -np.pi, np.pi
features = (ub - lb) * np.random.rand(num_samples, 1) + lb
labels = np.sin(features[:, 0]) + eps * (2 * np.random.rand(num_samples) - 1)
We still have to construct a feature map, an ansatz and combine them into a single quantum circuit for both quantum neural networks.
from qiskit.circuit import Parameter
num_inputs = 1
feature_map = QuantumCircuit(1)
feature_map.ry(Parameter("input"), 0)
ansatz = QuantumCircuit(1)
ansatz.ry(Parameter("weight"), 0)
circuit = QuantumCircuit(num_inputs)
circuit.compose(feature_map, inplace=True)
circuit.compose(ansatz, inplace=True)
We fix the initial point to get the same results from both networks.
initial_point = algorithm_globals.random.random(ansatz.num_parameters)
Building a regressor using OpflowQNN#
We create an OpflowQNN instance and re-use the quantum instance
created for the quantum kernel.
from qiskit.opflow import PauliSumOp, StateFn
from qiskit_machine_learning.neural_networks import OpflowQNN
observable = PauliSumOp.from_list([("Z", 1)])
operator = StateFn(observable, is_measurement=True) @ StateFn(circuit)
opflow_qnn = OpflowQNN(
operator=operator,
input_params=feature_map.parameters,
weight_params=ansatz.parameters,
quantum_instance=sv_qi,
)
Construct a regressor out of the network, train it and score it. In this case we use a gradient based optimizer, thus the network makes use of the gradient framework and due to nature of the dataset converges very quickly.
from qiskit.algorithms.optimizers import L_BFGS_B
from qiskit_machine_learning.algorithms import NeuralNetworkRegressor
regressor = NeuralNetworkRegressor(
neural_network=opflow_qnn,
optimizer=L_BFGS_B(maxiter=5),
initial_point=initial_point,
)
regressor.fit(features, labels)
regressor.score(features, labels)
0.9681198723451012
Building a regressor using EstimatorQNN#
Create an instance of the reference Estimator. You may create an estimator instance from QiskitRuntimeService to leverage Qiskit runtime services.
from qiskit.primitives import Estimator
estimator = Estimator()
Now, we create a instance of EstimatorQNN. The network creates an
observable as \(Z^{\otimes n}\), where \(n\) is the number of
qubit, if it is not specified.
from qiskit_machine_learning.neural_networks import EstimatorQNN
estimator_qnn = EstimatorQNN(
circuit=circuit,
input_params=feature_map.parameters,
weight_params=ansatz.parameters,
estimator=estimator,
)
Construct a variational quantum regressor and fit it. In this case we use a gradient based optimizer, thus the network makes use of the default estimator gradient that is created automatically.
from qiskit.algorithms.optimizers import L_BFGS_B
from qiskit_machine_learning.algorithms import VQR
regressor = NeuralNetworkRegressor(
neural_network=estimator_qnn,
optimizer=L_BFGS_B(maxiter=5),
initial_point=initial_point,
)
regressor.fit(features, labels)
regressor.score(features, labels)
0.9681198723451012
Instead of constructing a quantum neural network manually, you may train
VQR. It takes either a quantum instance or an estimator, depending
on what is passed it automatically constructs either TwoLayerQNN or
EstimatorQNN respectively.
Other notable deprecation#
A few other components, not mentioned explicitly above, are also deprecated or pending deprecation:
TwoLayerQNN is pending deprecation. Users should use EstimatorQNN instead.
The Distribution Learners package is deprecated fully. This package contains such classes as DiscriminativeNetwork, GenerativeNetwork, NumPyDiscriminator, PyTorchDiscriminator, QuantumGenerator, QGAN. Instead, please refer to the new QGAN tutorial. This tutorial introduces step-by-step how to build a PyTorch-based QGAN using quantum neural networks.
The Runtime package is deprecated. This package contains a client to Qiskit Programs that embed Qiskit Runtime in the algorithmic interfaces and facilitate usage of algorithms and scripts in the cloud. You should use QiskitRuntimeService to leverage primitives and runtimes.
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.25.0 |
qiskit-aer | 0.13.0 |
qiskit-machine-learning | 0.7.0 |
| System information | |
| Python version | 3.8.13 |
| Python compiler | Clang 12.0.0 |
| Python build | default, Oct 19 2022 17:54:22 |
| OS | Darwin |
| CPUs | 10 |
| Memory (Gb) | 64.0 |
| Thu Sep 14 13:57:31 2023 IST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.