How-to use pulse schedules generated by Qiskit Pulse with JAX transformations¶
Warning
This tutorial supresses DeprecationWarning instances raised by Qiskit Pulse in qiskit
1.3.
Qiskit Pulse enables specification of time-dependence in quantum systems as pulse schedules, built
from sequences of a variety of instructions, including the specification of shaped pulses (see the
detailed API information about Qiskit pulse API Reference). As of Qiskit 0.40.0, JAX support was added for
the ScalableSymbolicPulse class. This user guide entry demonstrates
the technical elements of utilizing this class within JAX-transformable functions.
Note
At present, only the ScalableSymbolicPulse class is supported by
JAX, as the validation present in other pulse types, such as
Gaussian, is not JAX-compatible.
This guide addresses the following topics. See the userguide on using JAX for a more detailed explanation of how to work with JAX in Qiskit Dynamics.
Configure JAX.
How to define a Gaussian pulse using
ScalableSymbolicPulse.JAX transforming Pulse to Signal conversion involving
ScalableSymbolicPulse.
1. Configure JAX¶
First, configure JAX to run on CPU in 64 bit mode.
# configure jax to use 64 bit mode
import jax
jax.config.update("jax_enable_x64", True)
# tell JAX we are using CPU
jax.config.update('jax_platform_name', 'cpu')
2. How to define a Gaussian pulse using ScalableSymbolicPulse¶
As the standard Gaussian pulse is not JAX-compatible, to define a
Gaussian pulse to use in optimization, we need to instantiate a
ScalableSymbolicPulse with a Gaussian parameterization. First, define
the symbolic representation in sympy.
from qiskit import pulse
from qiskit_dynamics.pulse import InstructionToSignals
import sympy as sym
dt = 0.222
w = 5.
# Helper function that returns a lifted Gaussian symbolic equation.
def lifted_gaussian(
t: sym.Symbol,
center,
t_zero,
sigma,
) -> sym.Expr:
t_shifted = (t - center).expand()
t_offset = (t_zero - center).expand()
gauss = sym.exp(-((t_shifted / sigma) ** 2) / 2)
offset = sym.exp(-((t_offset / sigma) ** 2) / 2)
return (gauss - offset) / (1 - offset)
Next, define the ScalableSymbolicPulse using the above expression.
_t, _duration, _amp, _sigma, _angle = sym.symbols("t, duration, amp, sigma, angle")
_center = _duration / 2
envelope_expr = (
_amp * sym.exp(sym.I * _angle) * lifted_gaussian(_t, _center, _duration + 1, _sigma)
)
gaussian_pulse = pulse.ScalableSymbolicPulse(
pulse_type="Gaussian",
duration=160,
amp=0.3,
angle=0,
parameters={"sigma": 40},
envelope=envelope_expr,
constraints=_sigma > 0,
valid_amp_conditions=sym.Abs(_amp) <= 1.0,
)
gaussian_pulse.draw()
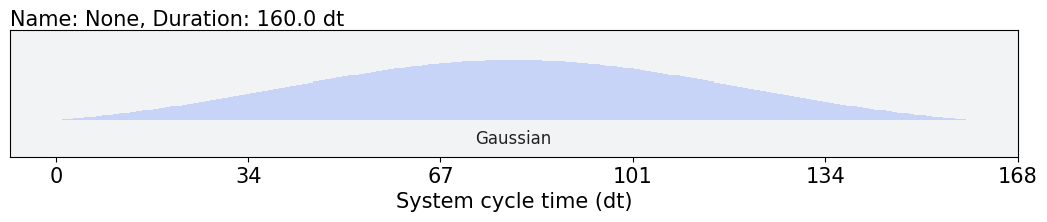
3. JAX transforming Pulse to Signal conversion involving ScalableSymbolicPulse¶
Using a Gaussian pulse as an example, we show that a function involving
ScalableSymbolicPulse and the pulse to signal converter can be
JAX-compiled (or more generally, JAX-transformed).
# use amplitude as the function argument
def jit_func(amp):
_t, _duration, _amp, _sigma, _angle = sym.symbols("t, duration, amp, sigma, angle")
_center = _duration / 2
envelope_expr = (
_amp * sym.exp(sym.I * _angle) * lifted_gaussian(_t, _center, _duration + 1, _sigma)
)
# we need to set disable_validation True to enable jax-jitting.
pulse.ScalableSymbolicPulse.disable_validation = True
gaussian_pulse = pulse.ScalableSymbolicPulse(
pulse_type="Gaussian",
duration=160,
amp=amp,
angle=0,
parameters={"sigma": 40},
envelope=envelope_expr,
constraints=_sigma > 0,
valid_amp_conditions=sym.Abs(_amp) <= 1.0,
)
# build a pulse schedule
with pulse.build() as schedule:
pulse.play(gaussian_pulse, pulse.DriveChannel(0))
# convert from a pulse schedule to a list of signals
converter = InstructionToSignals(dt, carriers={"d0": w})
return converter.get_signals(schedule)[0].samples
jax.jit(jit_func)(0.4)
Array([0.00461643+0.j, 0.00784044+0.j, 0.01118371+0.j, 0.0146479 +0.j,
0.01823455+0.j, 0.02194501+0.j, 0.02578049+0.j, 0.029742 +0.j,
0.03383034+0.j, 0.03804615+0.j, 0.0423898 +0.j, 0.04686147+0.j,
0.05146109+0.j, 0.05618834+0.j, 0.06104264+0.j, 0.06602316+0.j,
0.07112877+0.j, 0.07635807+0.j, 0.08170936+0.j, 0.08718063+0.j,
0.0927696 +0.j, 0.09847362+0.j, 0.10428977+0.j, 0.11021477+0.j,
0.11624505+0.j, 0.12237668+0.j, 0.12860541+0.j, 0.13492665+0.j,
0.14133549+0.j, 0.14782668+0.j, 0.15439464+0.j, 0.16103348+0.j,
0.16773697+0.j, 0.17449859+0.j, 0.18131147+0.j, 0.1881685 +0.j,
0.19506222+0.j, 0.20198494+0.j, 0.20892866+0.j, 0.21588517+0.j,
0.22284598+0.j, 0.22980239+0.j, 0.2367455 +0.j, 0.24366621+0.j,
0.25055524+0.j, 0.25740317+0.j, 0.26420043+0.j, 0.27093735+0.j,
0.27760417+0.j, 0.28419106+0.j, 0.29068813+0.j, 0.29708551+0.j,
0.30337328+0.j, 0.3095416 +0.j, 0.31558066+0.j, 0.32148073+0.j,
0.32723219+0.j, 0.33282555+0.j, 0.33825149+0.j, 0.34350085+0.j,
0.34856471+0.j, 0.35343437+0.j, 0.35810137+0.j, 0.36255757+0.j,
0.36679511+0.j, 0.37080648+0.j, 0.3745845 +0.j, 0.37812239+0.j,
0.38141374+0.j, 0.38445258+0.j, 0.38723335+0.j, 0.38975094+0.j,
0.39200072+0.j, 0.39397853+0.j, 0.39568069+0.j, 0.39710405+0.j,
0.39824594+0.j, 0.39910423+0.j, 0.39967732+0.j, 0.39996414+0.j,
0.39996414+0.j, 0.39967732+0.j, 0.39910423+0.j, 0.39824594+0.j,
0.39710405+0.j, 0.39568069+0.j, 0.39397853+0.j, 0.39200072+0.j,
0.38975094+0.j, 0.38723335+0.j, 0.38445258+0.j, 0.38141374+0.j,
0.37812239+0.j, 0.3745845 +0.j, 0.37080648+0.j, 0.36679511+0.j,
0.36255757+0.j, 0.35810137+0.j, 0.35343437+0.j, 0.34856471+0.j,
0.34350085+0.j, 0.33825149+0.j, 0.33282555+0.j, 0.32723219+0.j,
0.32148073+0.j, 0.31558066+0.j, 0.3095416 +0.j, 0.30337328+0.j,
0.29708551+0.j, 0.29068813+0.j, 0.28419106+0.j, 0.27760417+0.j,
0.27093735+0.j, 0.26420043+0.j, 0.25740317+0.j, 0.25055524+0.j,
0.24366621+0.j, 0.2367455 +0.j, 0.22980239+0.j, 0.22284598+0.j,
0.21588517+0.j, 0.20892866+0.j, 0.20198494+0.j, 0.19506222+0.j,
0.1881685 +0.j, 0.18131147+0.j, 0.17449859+0.j, 0.16773697+0.j,
0.16103348+0.j, 0.15439464+0.j, 0.14782668+0.j, 0.14133549+0.j,
0.13492665+0.j, 0.12860541+0.j, 0.12237668+0.j, 0.11624505+0.j,
0.11021477+0.j, 0.10428977+0.j, 0.09847362+0.j, 0.0927696 +0.j,
0.08718063+0.j, 0.08170936+0.j, 0.07635807+0.j, 0.07112877+0.j,
0.06602316+0.j, 0.06104264+0.j, 0.05618834+0.j, 0.05146109+0.j,
0.04686147+0.j, 0.0423898 +0.j, 0.03804615+0.j, 0.03383034+0.j,
0.029742 +0.j, 0.02578049+0.j, 0.02194501+0.j, 0.01823455+0.j,
0.0146479 +0.j, 0.01118371+0.j, 0.00784044+0.j, 0.00461643+0.j], dtype=complex128)